Теоретическая механика - теория, задания и примеры решения задач
Подождите немного. Документ загружается.


30
Таблица 1
N
P
Q
OA
AB
BC
CD
Номер
вариан-
та (рис.
11-13)
кН
кН
кН
м
м
м
м
1
7 6 5 3 2 2 1
2
1 2 3 2 5 1,5 1,5
3
2 4 5 1 3 2 4
4
5 6 8 6 5 4 2
5
7 1 4 7 5 4 2
6
3 7 4 2 5 3 4
7
3 7 9 1 4 5 6
8
4 6 8 2 3 4 8
9
5 4 2 3 4 5 10
10
4 8 3 1 2 4 3
11
3 4 8 3 2 4 2
12
9 8 7 2 3 4 6
13
5 5 3 3 4 6 2
14
7 4 2 4 3 6 –
15
5 8 4 2 4 7 5
16
5 7 4 4 8 4 6
17
2 3 5 2 4 3 2
18
5 4 6 4 6 2 –
19
2 4 5 1 2 4 3
20
4 3 7 3 4 6 8
21
6 7 9 2 6 2 4
22
2 4 6 1 4 6 3
23
4 7 5 2 5 8 3
24
9 7 5 2 6 4 2
25
2 3 4 3 4 3 5
26
4 5 3 4 6 4 10
27
3 4 2 2 5 3 2
28
3 3 3 2 4 6 6
29
4 3 2 2 4 3 8
30
5 4 3 4 6 4 10

31
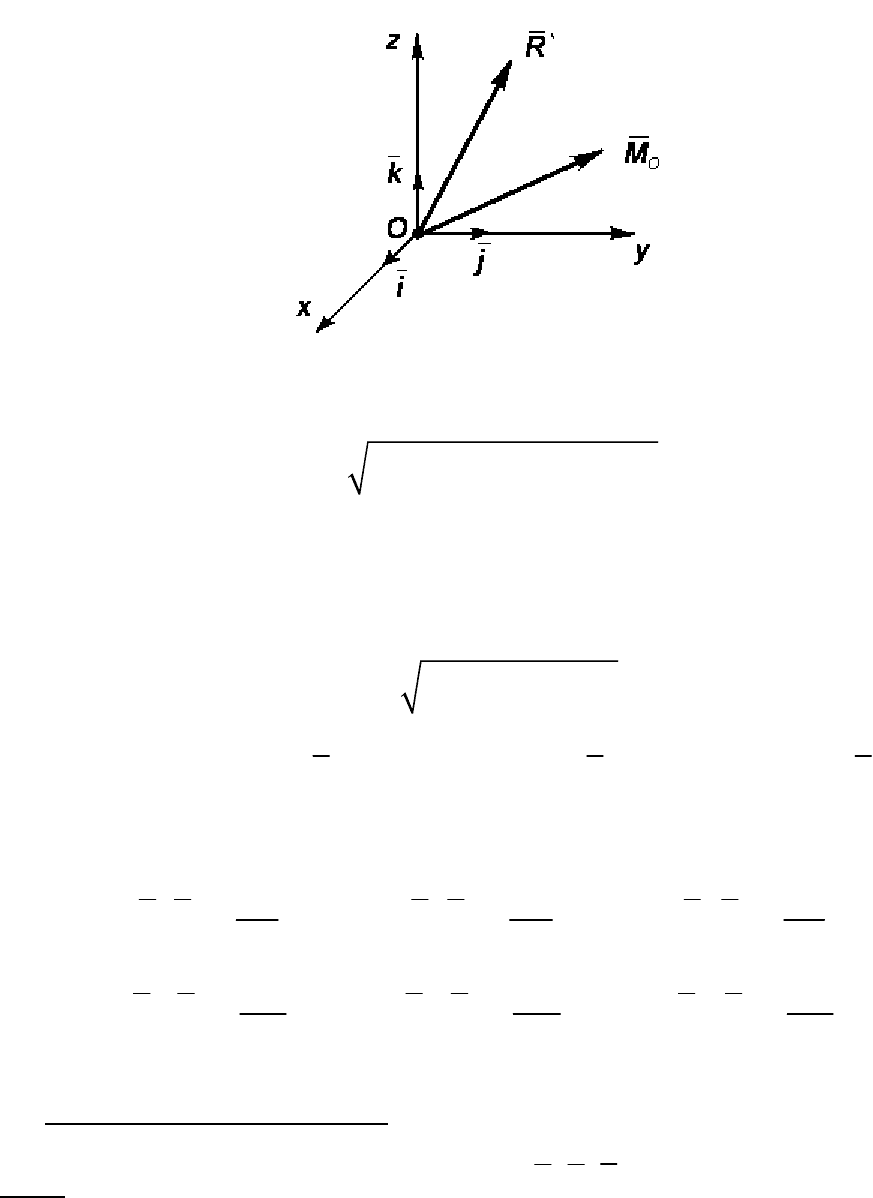
Пусть задана пространственная система сил
12
{ , ,..., }
n
FF F
(рис. 14 а) и показан центр приведения точка O.
а) б)
Рис. 14
Не меняя модули и направления сил переносим их в точку O с
собственными векторами-моментами этих сил относительно центра
приведения (рис. 14 б).
Тогда в центре приведения (т. O) получим два пучка векторов –
пучок векторов сил и пучок векторов – моментов.
Все силы геометрически сложим и получим главный вектор:
12
1
...
n
nk
k
RFF F F
=
′
=+++ =
∑
.
Векторы-моменты геометрически сложим, получим главный мо-
мент:
12
1
...
n
onk
k
MMM M M
=
=++ =
∑
.
На рис. 15 будем иметь два вектора
R
′
и
o
M в прямоугольной
системе координат xOyz.
Модуль главного вектора определится через его проекции
32
Рис. 15
222
R ()()()
xyz
RRR
′′ ′ ′
=++,
где
1
n
x
kx
k
RF
=
′
=
∑
;
1
n
y
ky
k
RF
=
′
=
∑
;
1
n
zkz
k
RF
=
′
=
∑
.
Модуль главного момента
222
oxyz
MMMM=++,
где
1
()
n
x
xk
k
MmF
=
=
∑
;
1
()
n
y
yk
k
MmF
=
=
∑
;
1
()
n
zzk
k
MmF
=
=
∑
.
Запишем направляющие косинусы для этих векторов:
n
cos( ; )
x
R
Ri
R
′
′
=
′
;
n
cos( ; )
y
R
Rj
R
′
′
=
′
;
n
cos( ; )
z
R
Rk
R
′
′
=
′
;
n
cos( ; )
x
o
o
M
Mi
M
=
;
n
cos( ; )
y
o
o
M
Mj
M
=
;
n
cos( ; )
z
o
o
M
Mk
M
=
.
Пример решения задачи
Дано: на рис. 16 показана система сил
{
;;
}
NPQ ; N = 2 кН;
P = 4 кН; Q = 6 кН; геометрические размеры – OA = 2 м; AB = 4 м;
BC = 6 м; CD = 3 м.
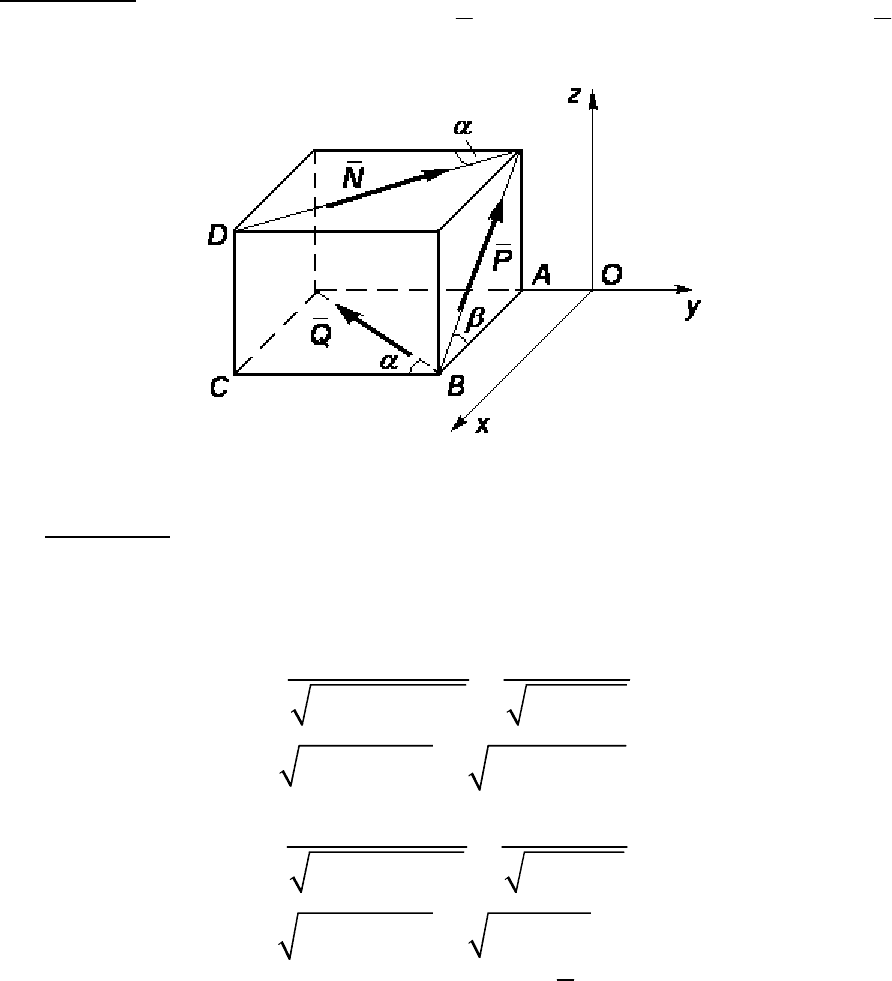
33
Требуется: привести все силы в заданный центр точку O, а затем вы-
числить модуль главного вектора
R
′
и модуль главного момента
o
M .
Рис. 16
Решение
Для решения задачи введем углы
α, β и найдем функции коси-
нусов и синусов этих углов:
22 22
6
cos α 0,832
46
BC
AB BC
===
++
;
22
sinα 1 cos 1 0,832 0,56
α
=− =− ≅
;
22 22
4
cosβ 0,8
43
AB
AB CD
===
++
;
22
sinβ 1cos 10,8 0,6
β
=− =− = .
Вычислим проекции главного вектора
R
′
на оси координат xOyz:
'
1
sinα sinα cosβ 2 0,56 6 0,56 4 0,8 1,28
n
xkx
k
RFN Q P кН
=
==−− + =−⋅−⋅+⋅=−
∑
;
1
cos α cos α 2 0,832 6 0,832 3,33
n
yky
k
RFN Q кН
=
′
== − =⋅−⋅=−
∑
;
1
sinβ 40,6 2,4
n
zkz
k
RFP кН
=
′
== =⋅=
∑
.
34
Определяем модуль главного вектора
222 2 22
() () () (
1, 2 8
)(
3,33
)
2, 4
xyz
RR R R
′′ ′ ′
=++=−+−+.
4,3R кН
′
≅
.
Вычислим проекции главного момента
o
M на оси координат:
1
() cosα sinβ
2 0, 832 3 4 0, 6 2 9, 8 ;
n
xxk
k
MmFN CDPOA
кНм
=
==−⋅−⋅=
=− ⋅ ⋅ − ⋅ ⋅ ≅−
∑
1
() sinβ sinα
4 0,6 4 2 0,56 3 12,96 ;
n
yyk
k
MmFPABNCD
кНм
=
==−⋅−⋅=
=− ⋅ ⋅ − ⋅ ⋅ ≅−
∑
1
() sinα cosβ sinα cosα
2 0,56 2 4 0,8 2 6 0,56 2 6 0,832 4 35,3 .
n
zzk
k
M m F N OA P OA Q OA Q AB
кНм
=
==−⋅−⋅−⋅−⋅=
=−⋅⋅−⋅⋅−⋅⋅−⋅ ⋅=−
∑
Модуль главного момента
222 2 2 2
(
9,8
)(
12,96
)(
35,3
)
o xyz
MMMM=++=−+− +− .
38,86
o
M кНм
=
.
Выбираем масштаб сил.
y
p
y
R
R
µ
′
=
′
; принимаем 50
y
R мм
′
=
; тогда
3,33
0,06
50
p
µ
=≅
()
кН
мм
;
1, 2 8
21,3
0,06
x
R мм
′
==
;
2, 4
40
0,06
z
R мм
′
==
.
Выбираем масштаб моментов.
z
M
z
M
M
µ
=
, принимаем
60
z
M мм=
;
тогда
35,3
0,588
60
M
µ
== ()
кНм
мм
;
9,8
16,7
0,588
x
M мм==
.
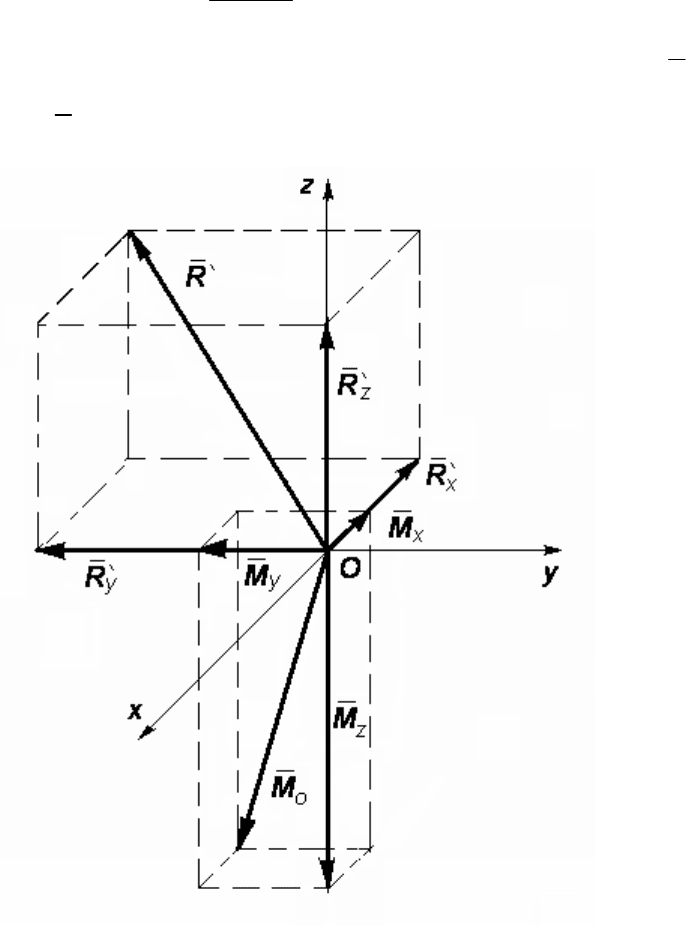
35
12,96
22
0,588
y
M мм==
.
На чертеже рис. 17 строим по проекциям главный вектор
'
R и
главный момент
o
M .
Рис. 17

36
Задача С.3. Произвольная пространственная
система сил
На пространственную конструкцию (рис. 18 – 27) действует сис-
тема сил
{;; ;; }FQQ PG
′
. Геометрические размеры a, b, c, d, e, r, h
и углы
α, β, γ, φ – заданы.
В данной задаче следует составить расчетные схемы для каждо-
го тела и записать в общем виде уравнения равновесия.
Произвольную пространственную систему сил можно привести в
заданный центр и получить главный вектор
1
n
k
k
RF
=
′
=
∑
и главный
момент
1
()
n
ook
k
MmF
=
=
∑
.
Если
0R
′
= и 0
o
M = , то данная система сил взаимно уравно-
вешивается.
Проецируя эти равенства на оси прямоугольной декартовой сис-
темы координат, получим шесть уравнений равновесия произволь-
ной пространственной системы сил:
Эти уравнения равновесия позволяют определить шесть неиз-
вестных величин. Поэтому при составлении уравнений нужно про-
верять, чтобы число неизвестных не было больше числа уравнений.
В противном случае задача будет статически неопределимой.
0;
0;
0;
kx
ky
kz
F
F
F
=
=
=
∑
∑
∑
()
0;
()
0;
()
0.
kx k
ky k
kz k
MF
MF
MF
=
=
=
∑
∑
∑
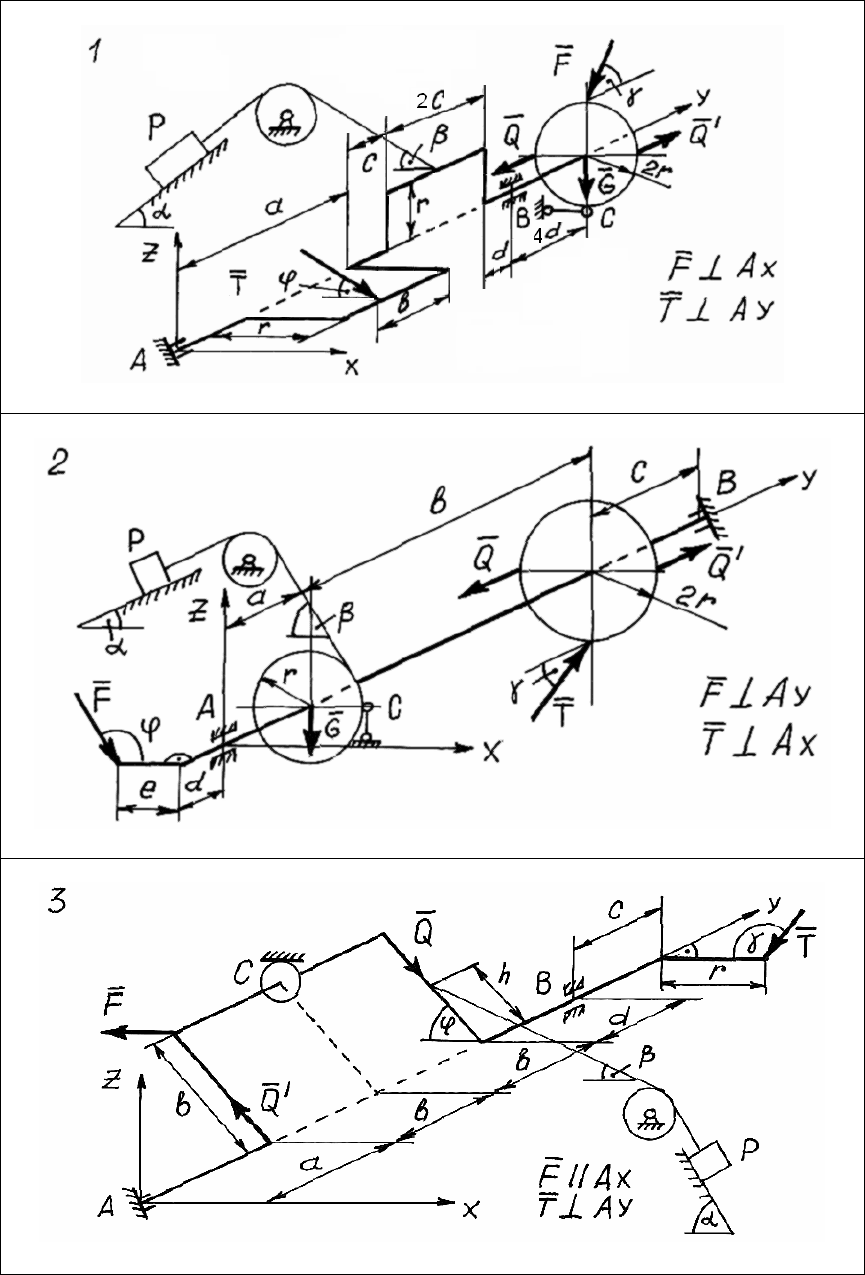
37
Рис. 18
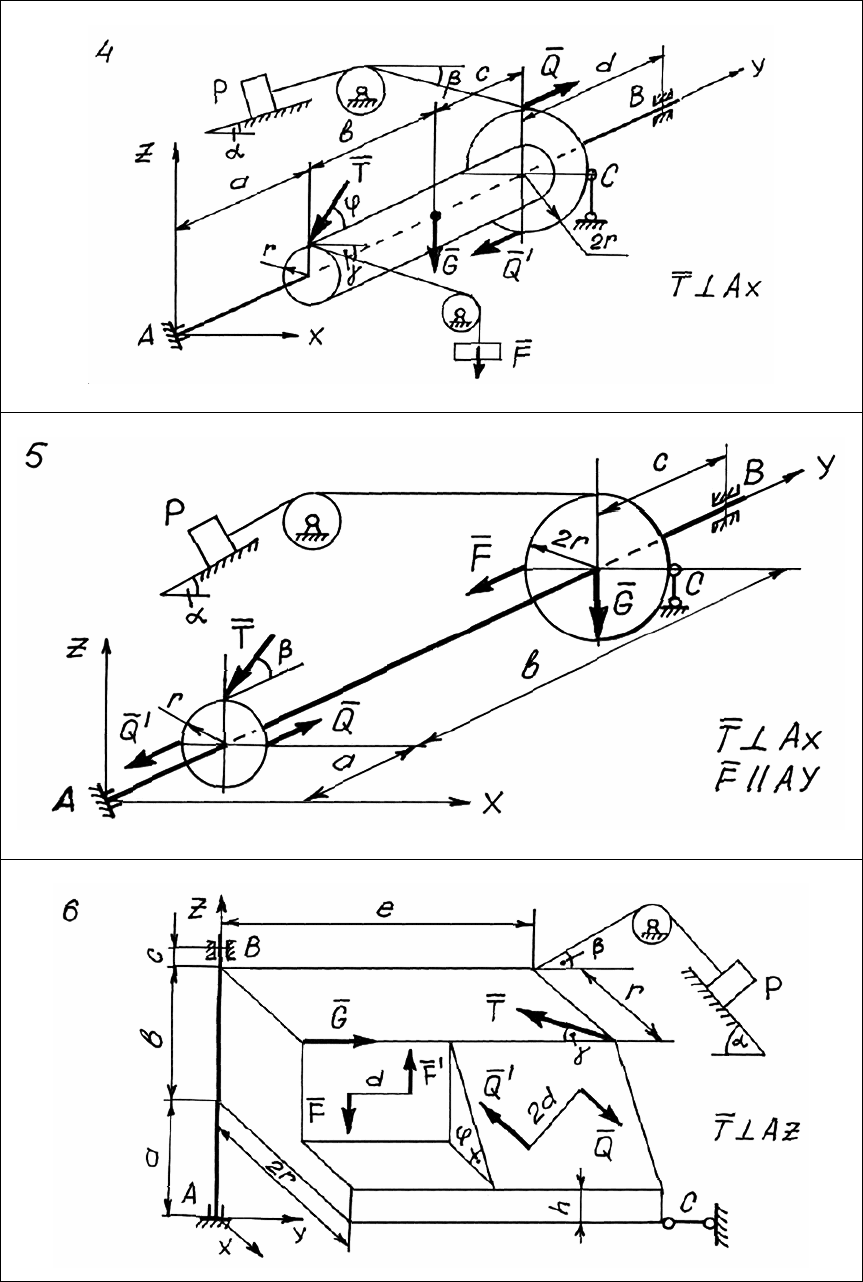
38
Рис. 19
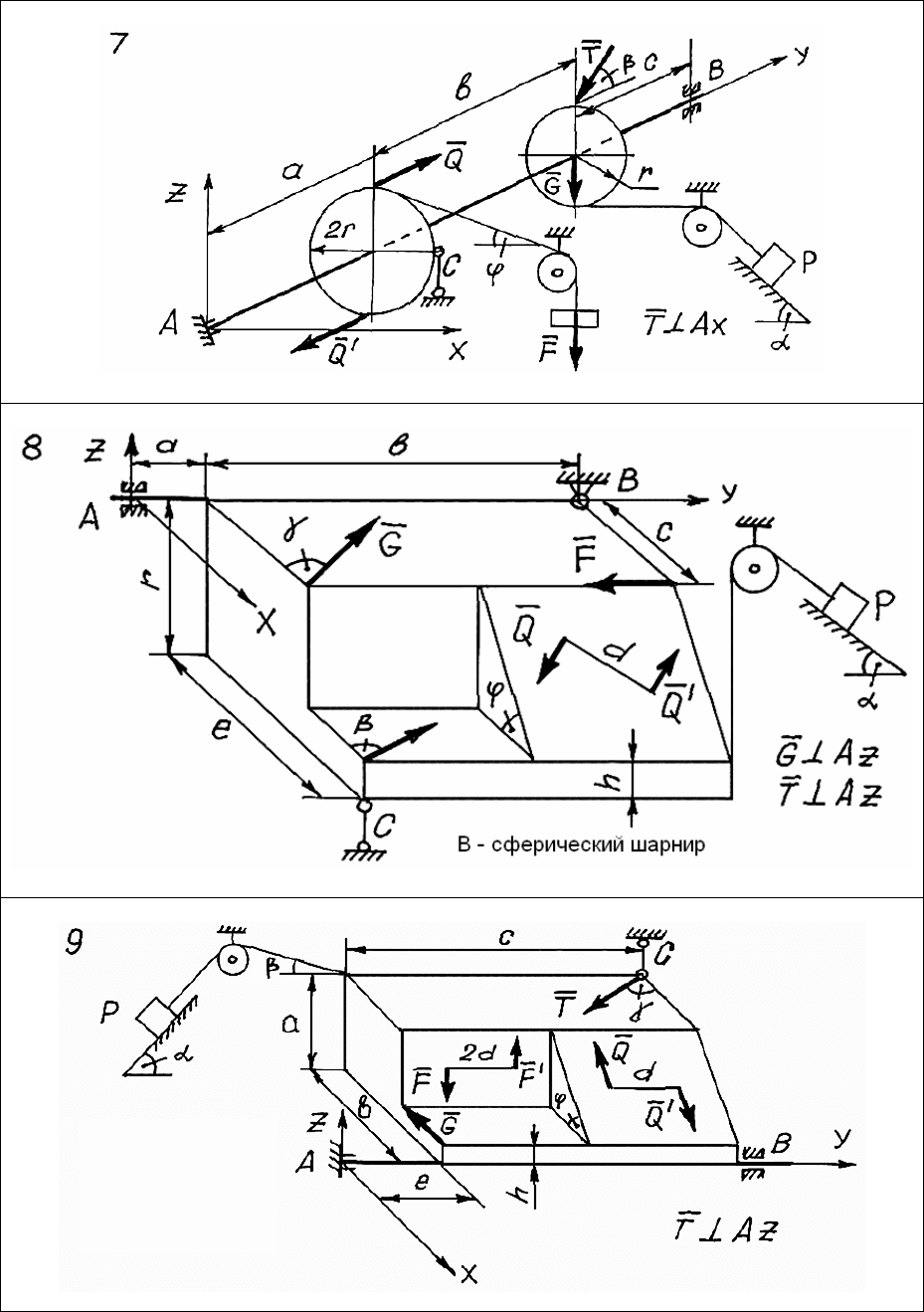
39
Рис. 20
