Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

Finally, the equation (17.1.34) takes the form

030

22 2

cos cos cos cos

sin sin

Mgl

MglJ

JMl

RR RR

−−

§·

=−

¨¸

©¹



(17.1.38)

From the first equation (17.1.37) it results that

cos cosRR> , while the relation

(17.1.38) shows that one must have

()

22 2

cos cos / 2 sin 1IMglJXR R R−<. If, at the

initial moment, we impart to the gyroscope a very great rotation

X , then we must have

−<<

cos cos 1RR; taking

RR R

<< 1R

, it results

cos cosRR−

()

cos 1 cosRR=−

sin sin sinRRRR+≅ and ≅

sin sinRR. The equation

(17.1.38) becomes

()

=−

1RMR NR



(17.1.38')

where

2sin

sin

Mgl

JMl

2sin

MglJ

(17.1.38'')

with the initial condition

(0) 0R = . By integration, using a substitution of the form

sin zNR

, we get

()

sin

tRMN

= ,

(17.1.38''')

whence

max

030

1/ 2 sin /MglJ IRN RX has a small value. As in Chap. 15,

Sect..2.1.2, to can appreciate easier the mode in which the motion of the gyroscope is

obtained and to determine easier its position, we consider the motion on the unit sphere

of centre

C of the piercing point of the movable axis

Cx with the very same sphere;

one obtains thus, in the motion of nutation, a curve contained in the interior of the

spherical zone bounded by the circles

and =+

max

RR R , the latter one being

the inferior circle. The period of motion is given by

22/QMN⋅

()

030

4sin/JJ Ml IQRX=+ , being as much smaller as the initial angular

velocity

X is greater. We notice that, in fact, the period of motion is in inverse

proportion to

X , while the amplitude of the motion (see the formula (17.1.38''')) is in

inverse proportion to

X . From the first equation (17.1.37) we get, analogously,

()

sin

sin 2

Mgl

ZR MN



(17.1.39)

MECHANICAL SYSTEMS, CLASSICAL MODELS

484

wherefrom, by integration,

()

() sin

Mgl

tt t

ZMNZ

ªº

=− +

«»

¬¼

(17.1.39')

Observing that

0X >

, the meridian plane being rotated in the same sense, it results

that the rotation axis of the gyroscope performs a motion of precession with an angular

velocity, which varies periodically between the value zero and a maximal value

max

2/Mgl IZX=



. The curve described in the motion of nutation on the unit sphere

between the circles

RR and =+

max

RR R is of the nature of the curve in

Fig. 15.21c, from the corresponding Lagrange-Poisson motion, having cuspidal points

for

and being tangent to the circle =+

max

RR R . Indeed, if V is the angle

made by this curve with a meridian circle, then we may write (see Sect. 15.2.1.2 too)

()

d1 1

tan sin sin 1 sin tan

dsin 2

RR RMN

=≅= +



. (17.1.40)

For

RR we have = 0R , while – if we take into account (17.1.38''') – it results

=tan 0V , hence cuspidal points; for →+

max

RRR one obtains →∞tanV , the

curve being normal to the meridian circle.

The point

P describes an analogous curve in the plane P (Fig. 17.9).

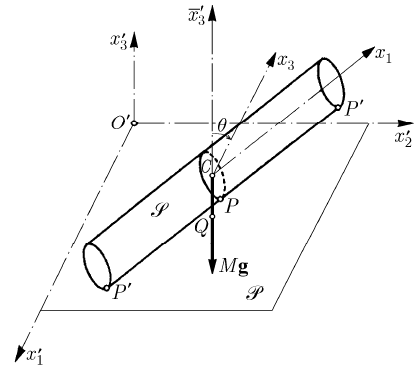
17.1.2.6 Frictionless Motion of a Homogeneous Rigid Solid of Cylindrical Form

on a Fixed Horizontal Plane

We consider, analogously, a homogeneous rigid solid S of cylindrical form, which lays

on a fixed horizontal plane

P along a generatrix PP

′′

. The fixed frame of reference

′

is linked to the plane P, the

′′

Ox -axis being normal to it, in the part in which is

the solid

S . The movable frame R is chosen so that the axes

,Cx Cx be in the

median transverse section, which attains the plane

P at the point P; the

-axis is

taken parallel to the generatrices of the cylinder (Fig. 17.10). The applicate

′

CQ S

of the centre

C will be given by a relation of the form (17.1.28) too. We also notice that

the

-axis is contained in the plane

Cx x

(we use also a frame of reference

, the

axes of which are parallel to the axes of the frame

′

), so that Euler’s angle is

= 0K

; the relations (5.2.35) become

XR=



sinXZR=



cosXZR=



(17.1.41)

The own weight

Mg and the constraint forces along the generatrix

′′

are along

the direction of the

′′

Ox -axis. From the theorem of motion of the mass centre, as in the

preceding cases, it results that the point

Q has a rectilinear and uniform motion in the

17 Dynamics of Systems of Rigid Solids

485

plane P ; analogously, we can reduce the general case to the case in which the point Q

is fixed. Observing that the moment of the given and constraint external forces with

respect to the

′′

Ox -axis vanishes, we can write a scalar conservation theorem of

moment of momentum in the form

const

′′′

′′ ′

⋅= =

Ki ; the formulae (14.1.23'),

(14.1.24'), with

and

′′

&vi, lead to

′

KIω , so that

()()

12 1 22 2 23 3 31 1 23 2 33 3

sin cos

III III KRX X X RX X X

′′

′

++ + ++ =

where we took into account the relations (5.2.36) with

= 0K and so that the axes

chosen for the frame

R are not, in general, principal axes. Introducing the relations

(17.1.41) too, we get

Fig. 17.10 Frictionless motion of a homogeneous rigid solid of

cylindrical form on a fixed horizontal plane

()

12 31 22 33 23

sin cos sin cos 2 sin cos

II I I I KRRR R R RRZ

′′

′

++++ =



(17.1.42)

We express the kinetic energy of the rigid solid

S with respect to the inertial frame of

reference

′

by means of the formulae (14.1.29'), (14.1.30'), with = 0

in the form

()

TMv

′′

=⋅ +

Iω ω ; if we take into account also the relations (17.1.41), the

conservation theorem of mechanical energy leads to the relation

()

22 2 2 2

11 22 33 23

() sin cos 2 sin cosIMf I I IRR R R R RZ

′

++++

ªº

¬¼



()

12 31

2sin cos 2()2II MgfhRRRZ R++ =−+



(17.1.43)

The differential equations (17.1.42), (17.1.43) allow to obtain Euler’s angles

()tZZ=

and

()tRR= . Eliminating Z



between these equations, we get a differential equation

MECHANICAL SYSTEMS, CLASSICAL MODELS

486

with separate variables, which gives the time t as a function of R, by a quadrature;

returning to the equation (17.1.42), we find Z as a function of R by a quadrature too. As

in the preceding cases, one can make a qualitative study of the solution. An interesting

particular case is that of the heavy homogeneous circular cylinder, case in which the

points

P and Q coincide, while () constf R = .

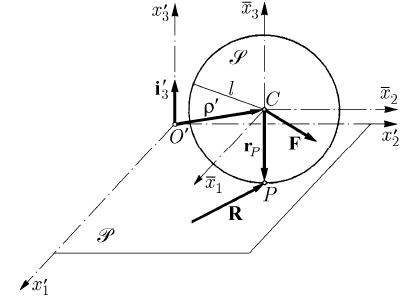
Let be now a

rigid solid sphere for which the repartition of masses is such that the mass

centre

C is just the centre of the sphere, the corresponding ellipsoid of inertia being a

sphere (

11 22 33

IIIJ===); for the sake of simplicity, we can assume that the

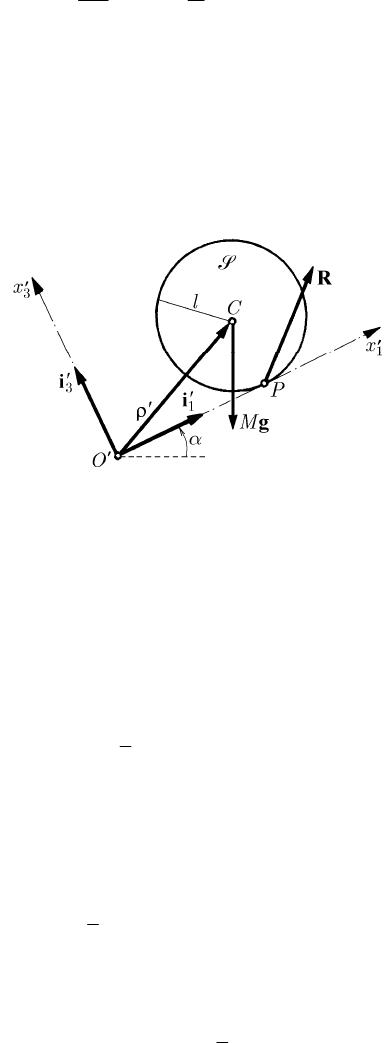
sphere is homogeneous. We suppose that the sphere of radius

l moves without sliding

on a fixed plane

P , taken as

′′′

Ox x -plane, the sphere being on that part of the plane

for which

′

> ; we assume, as well, that the sphere is acted upon by a force F,

applied at the centre

C (which, eventually, includes its own weight too), and by a

constraint force

R, applied at the contact point P (Fig. 17.11). We are in the hypothesis

in which, at the point

P, there does not exist sliding and the moments of rolling and

pivoting friction can be neglected. The mass centre

C moves in a fixed plane, parallel to

the plane

P and situated at a distance l of it; hence,

′′

⋅=

vi . From the imposed

conditions, it results

PC P

′′

=+×=

vv r0ω (

′

v is the velocity of the point of the

sphere which is in contact with the plane

P at the moment t ), where we use a frame of

Koenig. From the decomposition

Fig. 17.11 Slidingless motion of a sphere on a fixed plane

=+ω ω ω

′

⋅=

iω ,

′

×=

i0ω ,

we obtain

′′

=×viω , whence

17 Dynamics of Systems of Rigid Solids

17.1.2.7 Slidingless Motion of a Sphere on a Fixed Plane

487

′′

=×

ivω .

(17.1.44)

The constraint forces which arise between two rigid solids in contact are of the

nature of pressures, so that one must have

′

⋅≥Ri .

(17.1.45)

The theorem of motion of the mass centre gives

′



(17.1.46)

where

M is the mass of the sphere. In Koenig’s frame R , the moment of momentum

with respect to the centre

C is

J=K ω , so that the corresponding theorem of

moment of momentum reads

J =×



rRω . (17.1.47)

Using the decomposition of the vector

ω and taking into account (17.1.46), we also can

write

()

Jl MJ

′′

=×− −



iFω

ω .

Because the second member of this relation is a vector parallel to the fixed plane

P , it

results



0ω . Hence, the pivoting angular velocity

ω , is constant, so that it can be

specified by the initial conditions. The given force

F can be decomposed, as well, in the

form

=+FF F, with

′

⋅=

Fi ,

′

×=

Fi 0, so that we get

JMl l

′′′

+×=×



iiFω

, . Taking into account (17.1.44), we obtain, finally, the

equation of motion of the mass centre in the form

()

Ml l

′′′

×+ =×



iiF

ρ .

Because

′

constS , hence

′



, it results that the centre of mass C moves as a

particle of reduced mass

/MMJl, acted upon only by the given force

hence corresponding to the equation

′



(17.1.48)

The angular velocity vector is then given by

′′

=+×



ω ω

, const

JJJJG

ω .

(17.1.49)

The constraint force

MECHANICAL SYSTEMS, CLASSICAL MODELS

488

()

=− +

RFF

(17.1.50)

is given by (17.1.46), (17.1.48). The condition (17.1.45) leads thus to the condition

′

⋅≤

Fi ,

(17.1.45')

which must be fulfilled by the given force

F; the mechanical interpretation of this

condition is obvious. The conditions which ensure that the motion is without sliding

must be also fulfilled.

Fig. 17.12 Slidingless motion of a homogeneous sphere of

weight

M g on a plane inclined with the angle B

In particular, let us consider a homogeneous sphere of weight

Mg, which moves

slidingless on a plane inclined with the angle B with respect to the horizontal line.

Observing that

()

2/5JMl,

()

7/5MM,

sin

Mg B

′

=−Fi, where

′

i is the

unit vector of the line of greatest inclination of the plane in an ascendant orientation

(Fig. 17.12), we can write the equation (17.1.48) in the form

sin

g B

′′

=−



iρ

(17.1.51)

Hence, the motion of the centre

C is uniformly accelerated, the plane trajectory (in the

fixed plane

′

xl) being rectilinear or parabolical, corresponding to the initial

conditions. The formula (17.1.50) gives the constraint force in the form

sin cos

Mg BB

ªº

′′

«»

¬¼

Rii.

(17.1.52)

Because

cos

NMg B=

sin

TMgB=

17 Dynamics of Systems of Rigid Solids

489

the motion takes place without sliding if the angle B verifies the condition

()()

≤=tan 7 / 2 7 / 2 tanfBK, where f is the coefficient of sliding friction.

We notice that in the equation (17.1.51) does not intervene the radius

l of the sphere

S . As small would be this radius, the homogeneous sphere S , which rolls without

sliding on an inclined plane, cannot be assimilated to a particle; indeed, in case of a

particle the equation of motion is

-sing B

′′



ri.

17.1.2.8 Motion of a Heavy Homogeneous Sphere on a Fixed Horizontal Plane

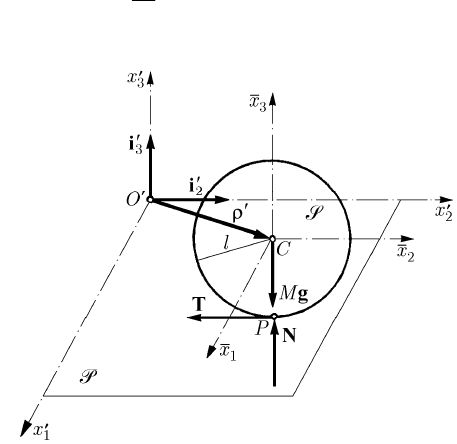
Let us consider a sphere S , the mass centre C of which coincides with the centre of the

sphere, of radius

l and weight Mg, which moves with friction on the horizontal plan P.

As till now, we choose the axes

′′

Ox and

′′

Ox in the plane P , the

′′

Ox -axis being

directed towards the part in which is the sphere

S (Fig. 17.13). At the contact point P

acts a constraint force having the component

N along the normal to the plane P and the

component

T contained in this plane. We use a movable frame of reference R with the

centre at

C, rigidly connected to the solid, the axes of which are specified by Euler’s

angles with respect to a frame

R of Koenig. We neglect the moments of rolling and

pivoting friction.

Fig. 17.13 Motion of a heavy homogeneous sphere on a fixed horizontal plane

The equation of motion of the mass centre

C is

′

=++



gNT

(17.1.53)

the motion of rotation about this centre being specified by

MECHANICAL SYSTEMS, CLASSICAL MODELS

490

J =×



rTω . (17.1.54)

Noting that

′

constlS , it results that M +=gN0 and M=Ng, wherefrom

TfMg= during the sliding; as a matter of fact, during this motion one must have a

relation of the form

′

=−Tv, where ()tMM= is a positive scalar. The equations

(17.1.53), (17.1.54) are reduced to

′



(17.1.53')

JMl

′′

+×



i0ω

= ,



0ω .

(17.1.54')

The velocity of the contact point

P of the sphere is given by

()

PC C

′′ ′ ′ ′

=+×−= ×vv i v iω − ω , so that it results

()

333

Ml Ml

§·

′′ ′′ ′′′ ′

=×=+××=+

¨¸

©¹

  



vv i i i− ω

ρ ρ ρ

MJ MJ

§·§·

′

=+ =− +

¨¸¨¸

©¹©¹

Assuming that the sphere is homogeneous, one can write

()

′′

=−



(17.1.55)

Hence, the velocity

′

v has a fixed direction of unit vector

′

i (we choose the

′′

Ox -axis so that to be parallel to this fixed direction, without any loss of generality).

As well, the constraint force

T will have a fixed direction; because = constT , it

results

constfMg

′

=− =

JJJJG

Ti too. Integrating the equation (17.1.55), we get

()

tv fgtt

ªº

′′ ′

=− −

«»

¬¼

vi.

(17.1.55')

We notice now, from the equation (17.1.53'), that the acceleration

′



of the mass centre

is constant in time, its trajectory being rectilinear or parabolical in the plane

′

lS ,

corresponding to the initial conditions; indeed,

() ()

tt tt

′′′′

−− + −+

(17.1.56)

The angular velocity vector is given by the equations (17.1.54') in the form

()

fMgl

ttt

′

−−+

iω = ω

=ω ω .

(17.1.57)

17 Dynamics of Systems of Rigid Solids

491

The magnitude

′

of the velocity of the point P with respect to the frame of

reference

′

decreases in time till vanishing at the moment

()

′

2/7 /

tt vfg

so that

()

′

=v0 and

()t =T0. Hence, the motion of the sphere takes place with

sliding, after the laws established above for

[

]

∈

,ttt; for ≥

tt the motion takes

place with rolling and pivoting but without sliding, corresponding to the results in the

preceding subsection. We notice that we must make

=F0 in (17.1.48), while

const

′′

JJJJG



vρ =

in (17.1.49); it results that the motion of the mass centre C becomes

rectilinear and uniform, the angular velocity vector

ω being constant in time (in space

and with respect to the sphere) .

Let us choose the axes

123

,,Cx Cx Cx of the non-inertial frame of reference R so

that the

Cx -axis be after the fixed support of the vector =

ω ω ; from Euler’s

equations (5.2.35), it results

cos sin sin 0RKZRK+=



, sin sin cos 0RKZRK−+ =



cosKZ R X+=



The determinant of the coefficients of the first two equations is

sin R ; if ≠ 0R , then it

results

==0RZ



, while the third equation gives =



. We get =

RR, =

ZZ,

()

=−+

000

ttKX K corresponding to the initial moment.

Coriolis observed that the equations (17.1.54') do not depend on the constraint force

T, taking place at any moment t (immaterial on the phase of motion); by integration, we

can write

′′

=×+

viω ω ,

const=

JJJJG

ω ,

(17.1.58)

as well as

()

′′

=×

viω − ω .

(17.1.58')

Choosing a point

()

0,0, /QJMl over the mass centre C, so that

()

JMl

′

=ri, it

results

()

/const

QC Q

JMl

′′ ′

=+×= ×=

JJJJG

vv r iω ω ; the vector

depends on

the initial conditions. In the second phase of the motion we have

′

v0, hence

′′

=×viω .

(17.1.59)

Replacing in (17.1.58'), we obtain

′′

=×

viω ,

(17.1.59')

MECHANICAL SYSTEMS, CLASSICAL MODELS

492

From (17.1.58') and (17.1.59'), one sees that – by sliding – the sphere

S moves away

from the pole

′

, in the first phase of the motion, and then comes near to the very same

pole, by rolling and pivoting without sliding.

In the first phase of the motion takes place the holonomic constraint relation

′

lS ,

(17.1.60)

the sphere

S having −=61 5 degrees of freedom. In the second phase of the motion

one has the relation (17.1.59), hence

d/d

vtlSX

′′ ′

d/d

vtlSX

′′ ′

==−

(after the axes of the frame of reference

′

); taking into account (5.2.35'), there

results two constraint relations of the form

()

d sin d sin cos d 0lSZRRZK

′

−− =

()

dcosdsinsind0lSZRRZK

′

++ =

(17.1.60')

Assuming that one can write an integrable relation of the form

()

,,,, 0f SSZRK

′′

imposing the condition

d0f = and taking into account (17.1.60'), we get

sin 0

l Z

∂∂

§·

¨¸

′

∂∂

©¹

sin cos sin 0

fff

l RZ Z

KSS

∂∂∂

§·

−+=

¨¸

′′

∂∂∂

©¹

∂

A partial differentiation of the first two relations with respect to Z, where we took into

account the third relation, leads to

cos sin 0

∂∂

′′

∂∂

sin sin cos 0

RZ Z

∂∂

§·

−=

¨¸

′′

∂∂

©¹

It results

′′

∂∂=∂∂ =

//0ffSSone obtains then ∂∂=∂∂=//0ffRK too. The

function

f depends on no one of the five variables; it results that one cannot determine

any integrable form, starting from the constraint relations (17.1.60'). Hence, these

relations are non-holonomic constraints. One can obtain this result also by using the

Theorem 3.2.1 of Frobenius. Thus, the sphere

S remains only with

()

−+ =612 3

degrees of freedom. The above results are verified, e.g., in case of the billiard ball.

17.1.2.9 Slidingless Motion of a Heavy Circular Disc on a Fixed Horizontal Plane

Let be a heavy rigid solid S, the centre of gravity C of which coincides with its centre,

bounded by a contour

C of radius l, which allows a motion without sliding on a fixed

horizontal plane

P ; we assume that the central ellipsoid of inertia is of rotation about

an axis

Cx normal to the plane of the contour C (

IIJ==). The fixed frame of

reference

′

has the axes

′′

Ox and

′′

Ox contained in the plane P, while the

′′

Ox -

axis is directed along the ascendent vertical; the frame

123

Cx x x is a frame of Koenig.

17 Dynamics of Systems of Rigid Solids

493