Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

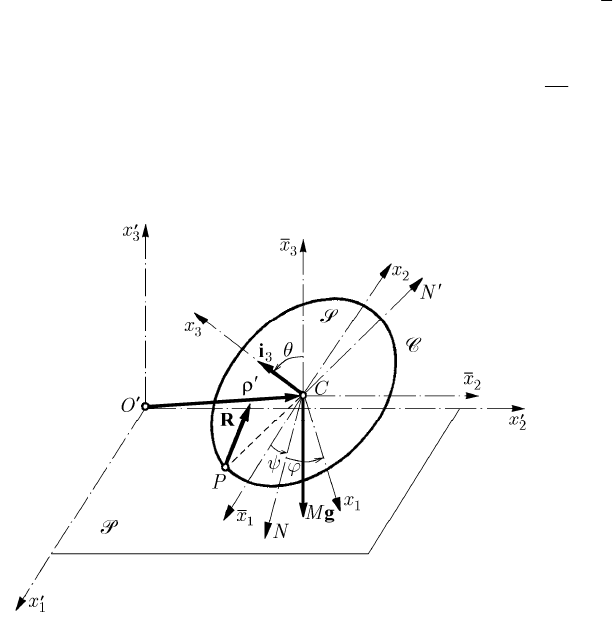
We draw the horizontal line of nodes CN, normal to the plane formed by the axes

and

; the

′

-axis, normal to the line of nodes, is situated along the line of

greatest slope of the plane of the contour

C . The movable frame of reference R ,

rigidly connected to the solid

S, is specified – with respect to the frame R – by

Euler’s angles Z, R and K. Upon the rigid solid

S acts the own weight Mg, at the

centre

C, and the constraint force R, at the contact point P; the moments of rolling and

pivoting friction are neglected (Fig. 17.14).

Fig. 17.14 Slidingless motion of a heavy circular disc on a fixed horizontal plane

We notice that the angular velocity vector will be given by

′

iω = ω , where

′

corresponds to the instantaneous rotation of the movable frame

R , of axes CN, CN

′

and

, with respect to the fixed frame

′

; the components of these vectors along

the axes of the frame

, will be

′

XXR





′

sinXXZR





cos cotXZRX R

′





, =+

cosXKZR







The equation of motion of the mass centre

()

′′′

+× = +



Rω

(17.1.61)

is written in the form

()

[

]

132

cot

CCC

Mv v v RXR

′′′

+− =







()

21 2

21 3

cot sin

CC C

Mv v v Mg RXRX R

′′ ′

+−=−+





 

(17.1.61')

()

12 3

321

cos

CCC

Mv v v Mg RXX R

′′′

+− =− +







MECHANICAL SYSTEMS, CLASSICAL MODELS

494

with respect to the frame

R . Because the rigid solid S has a central ellipsoid of

inertia of rotation, the moment of momentum with respect to the centre

C, in the frame

R , will have the components

KJX=



KJX=



KIX=



; Euler’s

equations

()

CCC

′

×=+



IIMM

ω + ω ω

(17.1.62)

can be written (we have

=M0 and

=×MrR

, the components of the vector

r in the frame

R , being 0, −l, 0)

()

133 2 2 3

cotJIJ lRXXXRX+− =−







()

233 2 1

cot 0JIJXXXRX−− =





(17.1.62')

33 1

IlRX







in the frame

R .

The rigid solid

S is rolling and pivoting without sliding on the plane P

only if the

velocity

PC P

′′

=+×

vv rω of its contact point P vanishes; in components on the axes

of the frame

R , it results

′

vlX



′



′

−=

vlX



(17.1.63)

We get thus nine equation (17.1.61'), (17.1.62'), (17.1.63) for the unknowns

′

 ,



and



, = 1, 2, 3j .

Eliminating the velocity of the mass centre between the equations (17.1.61') and

(17.1.63), we obtain

()

−=−

312 1

Ml RXXX







()

123 2

cot sinMl Mg RXXX R R+=−





(17.1.64)

()

123 3

cosMl Mg RXXX R+=− +







We can eliminate



between the last equation (17.1.62') and the first equation

(17.1.64); it results

()

3312

0IMl MlXXX+− =





. Associating the second equation

(17.1.62') and using the relation

XR=





, we get

()

IMl Ml

+−=



()

33 2

cot 0

JIJ

XXR

−− =





(17.1.65)

This system of differential equations determines the functions

()XXR=



()XXR=



. The first equation (17.1.65) gives

17 Dynamics of Systems of Rigid Solids

495

§·

¨¸

©¹



(17.1.66)

Replacing in the second equation (17.1.65), we find the resolvent equation of the

problem in the form

()

33 3

cot 0

Ml I

JI Ml

+− =





(17.1.67)

The constraint at

P being scleronomous, the elementary work of the constraint forces

vanishes; the conservation theorem of the mechanical energy gives

()()

222 22 2

12 33 3

123

CCC

Mv v v J I Mg hXX X S

′′′ ′

++ + + + =− +

 

(17.1.68)

Taking into account (17.1.63) and the relation

′

sinlSR, we can also write

() ( )

++++= +

22 2 22

123 3

2sin2JMl J I Ml Mgl hXX X R  .

(17.1.68')

After determination of the components

()XXR=



and

()XXR=



, this equation

allows the calculation of the component





. As a matter of fact, this equation is of

the form

()R'R=



; its discussion can be made as in the previous cases. It results,

finally,

()

tXX=



1, 2, 3

j =

; from (17.1.63), we obtain

()

Cj Cj

vvt

′′

=, while

(17.1.61') gives the components



, = 1, 2, 3j , of the constraint force.

Making the change of variable

cos sR , the problem is reduced to the

hypergeometric Euler-Gauss differential equation

()

[]

d() d()

11()0

ss s s

HBC BCX−+−++ −=





(17.1.69)

with

BC+=

()

Ml I

JI Ml

H = .

(17.1.70)

The general solution of this equation depends on two constants of integration M and N

and is expressed by means of the hypergeometric function in the form

() ( )

() , , ; 1 , 1 ,2 ;sF ssF s

XMBCHNBHCHH

−

= + +− +− −



(17.1.69')

In the particular case in which the rigid solid is a homogeneous circular disc of mass

M and radius l (e.g., a coin), we have =

/4JMl and =

/2IMl , so that

= 1/3BC , and if the rigid solid is a torus of mass M and of radius (of its axis) l,

MECHANICAL SYSTEMS, CLASSICAL MODELS

496

considered reduced to its axis, then we have =

/2JMl and =

IMl, wherefrom

= 1/4BC . Obviously, a and C have imaginary values and we can write

()()

1113

() , , ;cos cos , , ;cos

2222

FFXR M BC R N R B C R=+++



(17.1.71)

By a change of variable of the form

=cos sR , Korteweg obtains an equation of the

form (17.1.69) too, with

1BC+=

()

Ml I

JI Ml

, 1H = .

(17.1.70')

In the particular case of the torus,

= 1/4BC , so that ==1/2BC , obtaining the

solution

()

() , ,1;cos

FXR M R

 ,

(17.1.71')

which depends only on one arbitrary parameter.

If we take into account

()

cos sin sin

XRZKRZ

′′ ′

== +



iiω

()

sin sin cosRZKRZ

′

+−



()

cosZK R

′



i ,

()

123

cos sin cos cos sin

l RZ RZ R

′′′

=−−

riii,

the condition

′

+× =

vr0ω leads to the constraint relations

()

′

+−+=

cos cos sin sin cos 0lSZRZRRZKZ





()

′

+++=

cos sin sin cos sin 0lSZRZRRZKZ





(17.1.72)

cos 0lSRR

′

−=



The last relations is holonomic, obtaining the obvious relation

sinlSR, by

integration. The first two relations can be written, by simple linear combinations, in the

equivalent Pfaff forms

()

cos d sin d cos d d 0lZS ZS RZ K

′′

++ +=

sin d cos d sin d 0lZS ZS RR

′′

−−=

(17.1.72')

too, which are not integrable, the corresponding constraints being non-holonomic. The

rigid solid

S remains thus with

()

−+ =612 3 degrees of freedom.

17 Dynamics of Systems of Rigid Solids

497

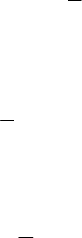
MECHANICAL SYSTEMS, CLASSICAL MODELS

17.2 Motion with Discontinuities of the Rigid Solids. Collisions

The problem of motion with discontinuities of the discrete mechanical systems has be

considered in Chap. 13, §1. In what follows, we will complete these results in case of

the rigid solids, studying the general phenomenon of collision of two arbitrary rigid

solids as well as some interesting particular cases. We put in evidence also the motion

of a rigid solid subjected to the action of a percussive force.

17.2.1 Percussion of Two Rigid Solids

After some general considerations concerning the phenomenon of collision, we present

a basic particular case: the centrical or the oblique collision of two spheres. We

consider then some technical applications which are of interest, as well as the general

case of collision of two rigid solids.

17.2.1.1 General Considerations on the Phenomenon of Collision

The general considerations in Sect. 13.1.1.1 concerning the phenomenon of collision in

case of a discrete mechanical system of particles remain valid in case of a discrete

mechanical system of rigid solids. The basic problem which is put consists in the

determination of the velocities of the points of the rigid solids after collision, assuming

that the corresponding velocities before this mechanical phenomenon are known. As

well, we mark out a phase of compression and a phase of relaxation (restitution), so

that the model of rigid solid is no more sufficient. We use, further, the notion of

percussion, as it has been defined in Chap. 10, Sect.. 1.2.3, starting from the notions of

force and impulse of the generalized force.

Using the results in Sect. 13.1.1.3 and Sect. 14.1.2.1, we can put in evidence the

jump relations corresponding to the discrete mechanical system

S of rigid solids,

reported to an inertial frame of reference

′

R and subjected to the action of given and

constraint, external and internal, percussive and non-percussive forces. By a process of

passing to limit in the sense of the theory of distributions, we express the theorems of

momentum and of motion of the mass centre in the form

()

MΔ=Δ =+HvRR,

(17.2.1)

where

()

ΔH and

()

Δv represent the jumps of the momentum of the mechanical

system

S and of the velocity of the mass centre C of this system, respectively, at a

moment of discontinuity, while by R and

R one has denoted the resultants of the given

and constraint external percussions, respectively, which act upon this system at that

moment.

The corresponding jump relation of the moment of momentum will be

()

Δ=+K MM,

(17.2.2)

where one has denoted by

()

ΔK the jump of the moment of momentum of the

mechanical system

S , with respect to the fixed pole O, at a moment of discontinuity,

498

while

M and

are the resultant moments of the given resultant percussions and of

the constraint external percussions, respectively, which act upon this system, with

respect to the very same pole, at that moment.

These results can be expressed synthetically in the form of a theorem of torsor,

which maintains its form with respect to a movable pole Q too. As well, this theorem

can be stated also with respect to a non-inertial frame of reference, in a continuous

motion with respect to an inertial frame; the basic equations of the mathematical model

of the collision phenomenon do not need a privileged frame. In the phenomenon of

collision of the considered mechanical system

S , the jump relations are thus invariant

to a change of frame or pole.

The theorems of Carnot and Kelvin in Sect. 13.1.1.5 can be applied also in the case

of the mechanical system

S considered above.

+=0RR in an interval of collision, then it results

()

Δ=H0 and

()

Δ=v0, hence the momentum of the mechanical system S and the velocity of the

mass centre of this system, respectively, are conserved in this interval. As well, if

+=0MM in an interval of collision, then

()

Δ=K0

, so that the moment of

momentum of the system remains constant in the respective interval.

Obviously, the above results take place also in the case of a single rigid solid

subjected to constraints. We mention that the constraints can be of four types:

(i) constraints which take place before the collision interval, in this interval or after it;

(ii) constraints which take place only in the collision interval or after it; (iii) constraints

which take place only before the collision interval or in this interval; (iv) constraints

which take place only in the collision interval.

Referring to a non-inertial frame of reference with the pole at the mass centre, the

jump relations (17.2.2) becomes

()

Δ=+I ω MM,

(17.2.3)

where we have put in evidence the jump of the rotation angular velocity vector in the

percussion interval. We can write, in components,

()

ij j

Ci Ci

IMMXΔ=+, 1, 2, 3i = ,

(17.2.3')

for a rigid solid. If the axes of the considered frame of reference are just the central

principal axes of inertia of the rigid solid

S , then we have

()

IMMXΔ= +

()

IMMXΔ= +

()

IMMXΔ= +

(17.2.3'')

In case of a rigid solid

S with a fixed point O, taken as pole of a non-inertial frame

of reference

R , we have

()

′

×+× ×



v = ω

ω ω

with respect to an inertial frame

′

R ; it results that

()

′

Δ=Δ×

v ω

, so that the theorem of motion of the mass

centre (17.2.1) takes the form

17 Dynamics of Systems of Rigid Solids

499

()

M Δ×=+ω ρ RR.

(17.2.4)

Analogously, in case of a rigid solid

S with a fixed axis, specified by the fixed

points

′

O and

O , the equations (14.2.1), (14.2.1') read

()

2111

MRRRXS

′

−Δ = ++

()

1212

MRRRXS

′

Δ=++

(17.2.5)

′

=++

3313

0 RRR,

()

31 12

IMlRXΔ= −,

()

23 11

IMlRXΔ= +, (17.2.5')

()

IMXΔ= ,

where

R are the components of the given percussions, while

′

R , = 1, 2, 3j ,

are the components of the constraint percussions at the fixed points

′

O and

O ,

respectively.

17.2.1.2 Centric Collision of Two Spheres

Let be two rigid spheres

and

S of masses

m and

m , the centres

O and

O of

which have the velocities

′

v and

′

v , respectively (we assume that

′′

, otherwise

the spheres can never be in collision), along the line

OO (Fig. 17.15,a); after

collision, the corresponding velocities will be

′′

v and

′′

v , respectively, and must be

determined (Fig. 17.15b). Because external percussions are not involved, we apply the

conservation theorem of momentum (the phenomenon is one-dimensional, so that there

intervene only the components of the velocities along the

Ox -axis, taking the

respective fixed pole on the line of the centres)

Fig. 17.15 Centric collision of two spheres: (a) before and (b) after collision

′ ′ ′′ ′′

+=+

11 22 11 22

mv mv mv mv

(17.2.6)

A second relation necessary to solve the problem (we have two unknowns:

′′

v and

′′

v ) is obtained by a mathematical modelling corresponding to the mechanical

MECHANICAL SYSTEMS, CLASSICAL MODELS

500

phenomenon. We consider thus a first phase of compression (

[

)

,ttt

′

∈

) which takes

place as long as the velocity of the centre

O is greater than the velocity of the centre

O , lasting till the equalization of the two velocities (

tt= ). The corresponding

percussions of this phase is

()()

11 2 2

Pmvv mvv

′′

=−= −

, where

is the

common velocity; it results

11 22

mv mv

′′

()

12 2 1

mm v v

′′

−

(17.2.7)

In the phase of relaxation (

(

]

,ttt

′′

∈

), the velocity of the centre

O continues to

decrease till

′′

v , and the velocity of the centre

O increases till

′′

v ; the percussion

corresponding to this phase is

()()

′′ ′′

=−=−

1122

Pmvv mvv, so that

11 22

mv mv

′′ ′′

()

12 2 1

mm v v

′′ ′′

−

(17.2.7')

Introducing also the coefficient of restitution (coefficient of elasticity by collision)

Pvv

′′ ′′

−

′′

−

(17.2.8)

we obtain the second relation, which is added to the relation (17.2.6). Finally, we can

write

()

11 12

vv k vv

′′ ′ ′ ′

=−+ −

()

22 12

vv k vv

′′ ′ ′ ′

=++ −

(17.2.9)

and one observe that

′′ ′′

< , the spheres moving away one from the other.

In the case in which

= 1k (hence, =

PP), the two spheres are compressed in the

first phase, returning then to the initial form; there corresponds a phenomenon of elastic

collision, the velocities after it being given by

()

[]

122121

2vmvmmv

′′ ′ ′

=+−

()

[]

211122

2vmvmmv

′′ ′ ′

=−−

(17.2.9')

= 0k (hence, = 0

P ), then the relaxation phase takes no more place; the spheres

adhere to each other and remain glued together, so that

()

12 11 22

vv mvmv

′′ ′′ ′ ′

== +

(17.2.9'')

17 Dynamics of Systems of Rigid Solids

501

The respective phenomenon is called plastic collision. Between these two limit cases

(for

01k<<) the spheres return practically to their initial forms, the phenomenon

being a natural collision (an elastic-plastic collision).

Taking into account (17.2.9), the loss of kinetic energy (

()

TTT%

′′′

=−

()( )

22 2 2

11 22 11 22

/2 /2mv mv mv mv

′ ′ ′′ ′′

=+ −+ ) is given by

()

Tkmvv%

′′

=− −

111

mm m

(17.2.10)

In case of an elastic collision, we have

()

0T% =

, the phenomenon taking place

without loss of kinetic energy; in case of a plastic collision, we find again the formula

(13.1.77). The lost kinetic energy is transformed in work of deformation, in caloric or

luminous energy etc.

mm= (it is not necessary that the spheres be identical), we get

()()

[]

112

vkvkv

′′ ′ ′

=−++ ,

()()

[]

221

vkvkv

′′ ′ ′

=−++ .

(17.2.9''')

In case of an elastic collision, it results

′′ ′

= and

′′ ′

= , the spheres transmitting

the energy each other. In particular, if

′

= , then we have

′′

= too; hence, if an

elastic sphere

S strikes, with a velocity

′

, another elastic sphere

S , having the

same mass and being at rest with respect to a given inertial frame of reference, then it

transmits to the latter one its velocity

′

and then stops.

17.2.1.3 Technical Applications

A particular case of the problem considered at the preceding subsection, interesting for

technical applications, is that of the plastic collision of a sphere

S of mass

m and

velocity

v with another sphere

S of mass

m , at rest with respect to a given frame of

reference. If we make

′

= in (17.2.9''), then we obtain

12 1

vv v

′′ ′′ ′

(17.2.11)

As well, the relation (17.2.10) reads

()

Tmv%

′

(17.2.11')

The relative loss of kinetic energy with respect to the kinetic energy before collision

(

()

1/2Tmv

′

= ) will be

()

Tmm

(17.2.11'')

These results of theoretical nature (the considered mathematical modelling) can be

successfully used for different technical applications, e.g., in case of beating a nail with

MECHANICAL SYSTEMS, CLASSICAL MODELS

502

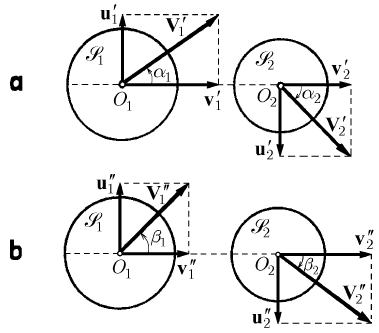
a hammer (

m is the mass of the hammer,

m is the mass of the nail, while

′

is the

velocity with which the hammer beats the nail) or in case of beating a pilot with a

rammer (

m is the mass of the rammer,

m is the mass of the pilot, while

′

is the

velocity with which the rammer beats the pilot). It is important, in both cases, that the

relative loss of kinetic energy be as small as possible; one observes, from (17.2.11''),

that the ratio

/mm must be as great as possible, hence the mass of the hammer (or

the rammer) must be much more greater than the mass of the nail (pilot).

In case of a process of working up a piece (bending, adjustment, rivetting etc.) it is

useful a greater loss of kinetic energy, which is transformed in work of deformation.

The ratio

()

/TT% is as greater as the ratio

/mm is smaller, so that the hammer

must have a small mass

m , while the piece to be worked up must have a great mass

m . Thus, the piece to be worked up is put on a bench (e.g., an anvil), increasing thus

the mass

m . As well, in case of rivetting, the rivet head bears on a special metallic

piece (a rivetting knob), increasing much its mass

m .

17.2.1.4 Oblique Collision of Two Spheres

Let be once more the two spheres

S and

S , of centres

and

and masses

and

m , the centres of which have the velocities

′

V and

′

V , respectively (with respect

to a given fixed frame of reference); the supports of these velocities are no more

directed along the line of the centres and have the components

′

v and

′

v (

′′

> )

along this line and the components

′

u and

′

u normal to it (Fig. 17.16a). After

collision, these velocities become

111

′′ ′′ ′′

Vvu,

222

′′ ′′ ′′

Vvu, the notations

corresponding to the precedent ones (Fig. 17.16b). If

B and

B are the angles made

by the velocities

′

V and

′

V , respectively, with the line of centres, there results

Fig. 17.16 Oblique collision of two spheres: (a) before and (b) after collision

11 1

cosvV B

′′

11 1

sinuV B

′′

22 2

cosvV B

′′

22 2

sinuV B

′′

17 Dynamics of Systems of Rigid Solids

503