Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

For linearization, we assume – further – that ≅

RR so that

()

−

211 1

RRR R



 and

()

−

212 2

RRR R



 ; we may write

++ =

11 2 1

BR R CR

 

++ =

22 1 2

BR R R

 

(17.1.4'')

We search solutions of the form

() e

RM, =

() e

RM and are led to

()

++=

11 2 1

BM M T CM

()

++=

22 1 2

BM M T M

;

(17.1.5)

one must have

()()

(

)

−−+−=

12 1 2

BB T B CB T C ,

wherefrom

()

ªº

=− + ± − +

¬¼

−

12 12

TBCBBCBC

(17.1.5')

so that the linear algebraic system in

M and

M be compatible. Noting that the

discriminant of the biquadratic equation is always positive, that the magnitude between

the square brackets is also positive and that

1MM we can state that <

0T .

Denoting by

iN , ±

iN the corresponding roots and determining

, MM from the

system (17.1.5), one obtains the general solution of the linearized system (17.1.4'') in

the form

(

)

()

(

)

()

() ( )

11211122222

2 11112222

() cos cos ,

( ) cos cos ,

tC t C t

RBNNKBNNK

RNNKNNK

=− −+− −

=−+−

(17.1.6)

where

C ,

K ,

K are arbitrary constants, which are determined by the initial

conditions. The system

S oscillates so that the amplitudes of any oscillation are small

(hence, the constants

C and

C too), the pulsations

N and

N being, in general,

distinct.

We can make an analogous study of the double pendulum choosing as unknown

functions the co-ordinates

′

211

() sinxt l R and =

222

() sinxt l R of the mass centres

C and

C , respectively.

We may put the problem to find the conditions in which the mechanical system

oscillates as a unitary rigid solid; in this case, we must have

() ()ttRR



. Assuming

that

() () ()tttRRR too, the equations (17.1.4) become

MECHANICAL SYSTEMS, CLASSICAL MODELS

464

()

++ =

1sin0

BR C R



()

++ =

1sin0

BR R



;

(17.1.7)

we are led to the same solution if the relation

()

+= +

11BC B takes place, hence

()()

[

]

+− +− =

22 22 2

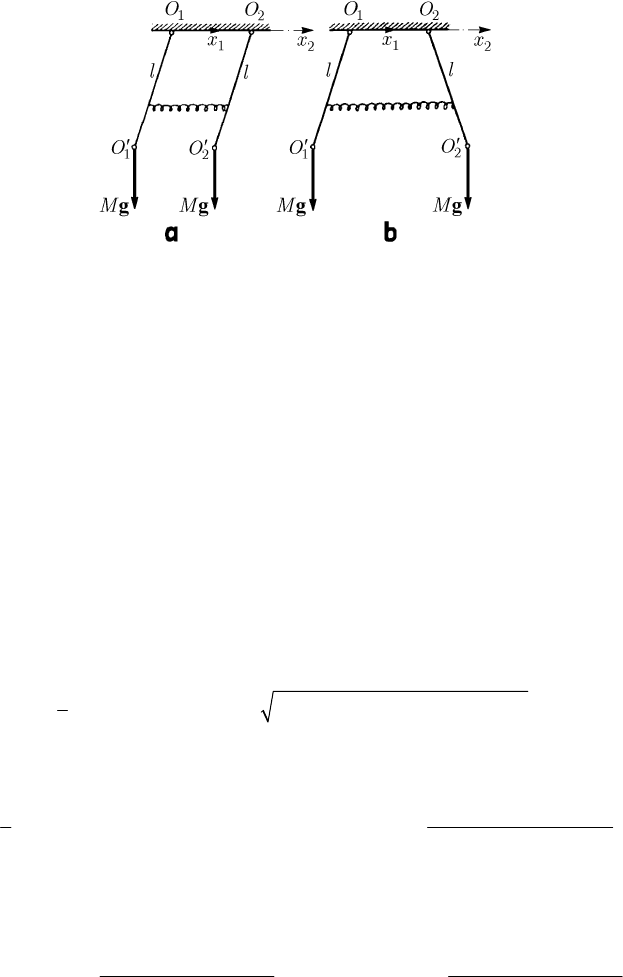
12 1 1 1 2 2 12 22

Mli l li l lll Mli,

(17.1.7')

even in case of finite amplitudes. It is sufficient to have

≅

RR in the case of small

motions. The two equations (17.1.7) correspond thus to a synchronous mathematical

pendulum of length

()

′

1ll B hence of length

′

=+ +

lll l,

(17.1.7'')

where

222

/0lil

; we notice thus that

′′

lOO

, the point

′

being on the other

part of the mass centre

C , with respect to the point

O (Fig. 17.1,b).

A bell together with its tongue forms a double pendulum, subjected to small

oscillations. If, by construction, the condition (17.1.7') takes place, then the bell does

not ring (no sound is heard, because the tongue cannot strike the bell). Such a

phenomenon took place in reality, remaining famous, at the inauguration, in 1876, of

the bell of the cathedral in Cologne; this bell has been put in form from the bronze of

the guns conquered by the Prussian army at Sedan, in 1870, in the campaign against

France.

Returning to the non-linear system of differential equations of second order (17.1.4),

we introduce the notation

zR , =



, =



, so that the system

becomes now of first order and reads



, =



() ()

+−−−+=

ªº

¬¼

3421421 1

cos sin sin 0zzzzzzz zBC

(17.1.8)

() ()

+−+−+=

ªº

¬¼

4321321 2

cos sin sin 0zzzzzzz zH ,

where

()

4/3

B ,

()

4/3

, =

(17.1.8')

are non-dimensional coefficients with

, =

(17.1.8'')

Using the theory of Lie transform applied by L. Morino, F. Mastroddi and M. Cutroni

in 1992, Anca Zlătescu studied, in 1998, in her doctor thesis, the system (17.1.8),

assuming that

17 Dynamics of Systems of Rigid Solids

465

()

1cos

≅+ −

−−

(17.1.8''')

She put in evidence also the effect of this approximation, as well as the influence of the

generalized forces of vibrating type applied at the points

C or

′

, which introduce

perturbing terms in the second members of the last two equations (17.1.8). In this order

of ideas, she dealt with the conditions of stability of the motion; the passing to chaos

has been taken into consideration too.

Analogously, one can study the problem of the triple pendulum.

17.1.1.3 Sympathetic Pendulums

Let be a mechanical system

S formed of two identical (in tune) or distinct (out of time)

physical pendulums, linked between them (stronger or weaker) by an elastic spring;

these pendulums which oscillate simultaneously are called sympathetic (coupled)

pendulums. We mention the analogy between this system and a device formed of two

electrical circuits (one primary and one secondary) inductively connected. If

l and

are the lengths of the mathematical pendulums synchronous with the considered

sympathetic pendulums, then the pulsations are given by

/glX , =

/glX ; the

elastic constants involved are

/kMT , =

/kMT , where

and

are the

masses of the pendulums, while

T is the stress in the spring for a unit linear strain

(Fig. 17.2).

Fig. 17.2 Sympathetic Pendulums

If, in particular, the sympathetic pendulums are perfectly in tune, then we can write

the equations of motion in the form (

lll

, ==

120

XXX,

MMM

kkk

)

()

11 12

xxkxxX+=−−

()

22 21

xxkxxX+=−−

(17.1.9)

where

x and

x are the elongations of the corresponding centres of oscillation

′

O and

′

O . The change of variable =−

112

xxY , =+

212

xxY leads to the equations

()

20kYX Y++ =



0YXY+=



(17.1.9')

MECHANICAL SYSTEMS, CLASSICAL MODELS

466

with the pulsations =+≅

2kXX +

/kXX,

′

XX. Assuming that at the

initial moment

0t = we have =

xa, =



, =

0x , =



, hence

aYY , ==

0YY



, we get

()cos ta tYX,

()cos ta tYX

′

and then

(

()

112

/2x YY=+ ,

()

221

/2x YY=− )

()

( ) cos cos cos cos

222

xt t t a

XX XX

′′

−+

′

=+=

()

() cos cos sin sin

222

xt t t a

XX XX

′′

−+

′

=−=

(17.1.9'')

Fig. 17.3 Sympathetic pendulums: Graphics of the elongations

of the points

′

(a) and

′

(b)

The graphics of the elongations of the points

′

O and

′

O are drawn in Fig. 17.3a

and b, where the variation of the amplitude (vibrations with modulation in amplitude)

is represented by broken lines; if

()

/2 /2kXX X X

′

−≅

 , then the connection of

the pendulums is a weak connection, the amplitude varying slowly in time (we can say

that a fluctuation of the amplitude takes place). One can see that the vibration of each

physical pendulum can be obtained by the superposition of two fundamental vibrations;

to a constructive interference (maximal amplitude) of one pendulum corresponds a

destructive interference (which is an extinction) for the second pendulum. Each of the

two pendulums leads to a phenomenon of beats (see Chap. 8, Sect. 2.2.4 too). The

mechanical energy passes from a pendulum to another one.

There are two cases in which this energy transfer does not take place: the symmetric

case (Fig. 17.4a) in which

/2xxa, ==

0xx



, resulting

() ()xt xt=

()

′

/2 cosatX and the antisymmetric case (Fig. 17.4b) in which

=− =

/2xxa, ==

0xx



, obtaining

()

() () /2 cosxt xt a tX=− = . These

vibrations represent the two fundamental vibrations (principal vibrations or proper

vibrations) of the sympathetic pendulums, which take place without transfer of energy,

corresponding to the number of degrees of freedom of the mechanical system. One

observes that the equations (17.1.9') are just the differential equations of these two

17 Dynamics of Systems of Rigid Solids

467

vibrations. The vibrations (17.1.9'') are obtained by superposing the effects of the two

fundamental vibrations.

Fig. 17.4 Sympathetic pendulums: a) symmetric case; b) antisymmetric case

If the two pendulums are out of tune (the general case) then the equations of motion

read

()

111 112

xxkxxX+=−− ,

()

222 221

xxkxxX+=− − .

(17.1.10)

Putting

O±

, we get the homogeneous algebraic system

()

−+ − =

11112

0kA kAXO ,

()

−+ − =

22221

0kA kAXO ;

the condition of compatibility leads to the biquadratic equation

()

[

]

()

[

]

−+ −+ =

22 22

11 22 12

kkkkOX OX ,

wherefrom

()

222 22

1212 1212 12

kk kk kkOXX XX

ªº

= + ++± − +− +

«»

¬¼

both roots being positive. Expanding the radical after Newton’s binomial, we get

()

½

ªº

°°

≅ + ++± − +− +

«»

®¾

−+−

«»

°°

¯¿

¬¼

222 22

1212 1212

1212

kk kk

OXX XX

for

and

small (hence for a weak connection); the pulsations X and

′

X will be

given by

()

11 22

=++

+− +

()

11 22

′

=+−

+− +

(17.1.10')

MECHANICAL SYSTEMS, CLASSICAL MODELS

468

One obtains thus elongations of the form

()

( ) cos sin cos sinxt A t B t A t B tHX XH X X

′′ ′ ′ ′

=++ +

( ) cos sin cos sinxt A t B t A t B tXX X X

′′′′

=++ +

(17.1.10'')

where

H and

′

H correspond to the non-determinate solutions of the homogeneous

linear algebraic system. With the initial conditions (for

0t = )

0x =

0x , =



, it results

()

() cos cos

xt t t

HXHX

′′

=−

′

−

()

() cos cos

xt t t

′

=−

′

−

()()

sin sin

XX XX

′′

−+

′

−

(17.1.10''')

Fig. 17.5 Sympathetic pendulums out of tune. Graphics of the elongations

of the points

′

(a) and

′

(b)

The graphics of these elongations are drawn in Fig. 17.5a and b. One observes that, in

this case, the destructive interference of the first pendulum does not lead to extinction

after intervals of time equal to

()

′

−

2/QXX.

An analogous study can be made choosing as unknown functions the angles

()

111

() arcsin /txlR = and

()

222

() arcsin /txlR = made by

′

OO and

′

OO with

the descendent vertical line, respectively.

We denote

OO l and

11 22

OQ OQ a==, where

and

are the ends of the

elastic spring, characterized by the elastic constant

k; the elastic force in the spring is

thus given by

12 12

kOO QQ− . We notice that

()

[]

()

12 2 1 2 1

sin sin cos cosQQ l a aRR RR=+ − + −

() ()

[]

=+ − + − −

21 21

2sin sin 2 1coslal aRR RR.

(17.1.11)

17 Dynamics of Systems of Rigid Solids

469

The non-linear system of equations of motion is obtained in the form

()

11 1 1 1 1 2

sin 0

IMgl lQQRR

∂

++−=

∂



()

22 2 2 2 1 2

sin 0

IMgl lQQRR

∂

++−=

∂



(17.1.12)

Introducing the expression of

, it results

()

[]

11 1 1 1 1 2 1

sin cos sin 0I M gl kaH l aRR RRR++ +−=



()

[]

22 2 2 2 2 2 1

sin cos sin 0I M gl kaH l aRR RRR+− +−=



(17.1.12')

where

()

−

:RR

(17.1.11')

with

() () ()

[]

{}

12 12 2 1 2 1

,2sinsin21cosQQ l al a:RR R R R R==+ − + − − .

(17.1.11'')

Using the notations

Mgl

122

MMgl

C =

' =

Y =

alM

B =

alM

B =

(17.1.13)

as well as

()

−

=−

1/2

,1HR R ' ,

(17.1.13')

with

() ( ) ( )

[]

12 2 1 2 1

,12sinsin21cos'R R Y R R Y R R=+ − + − − .

(17.1.13'')

Introducing the unknown functions

z R , =

z R



, =

z R



, the system of

differential equations of second order takes the form of a system of first order

zz=

() ( )

[

]

=− − + −

3112121

sin , cos sinzwz zz z zzHB Y



(17.1.12'')

()

[

]

4212221

sin , cos sinzwzzz z zzCHBY=− + + − .

MECHANICAL SYSTEMS, CLASSICAL MODELS

470

These equations have been introduced in 2001 by ùtefania Donescu in her doctor thesis.

She studied them using the linear equivalence method (LEM) established by Ileana

Toma in her doctor thesis, in 1980 (see Chap. 24, Sect. 1.2), assuming that

() ()

[]

21 21

2sin sin 2 1cos 1YR R Y RR−+− −<,

(17.1.13''')

wherefrom

() () ()

[]

≅− − − − −

12 2 1 2 1

,sin 1cosHR R Y R R Y R R ;

(17.1.13

)

this approximation has been thoroughly discussed. ùt. Donescu dealt also with cnoidal

solutions, obtaining numerical results plotted into diagrams, as well as interesting

results concerning the stability of the mechanical system, both for the approximate case

and for the exact one.

17.1.2 Contact of Two Rigid Solids

In what follows, we consider firstly the general case of the rigid solid in contact with a

fixed surface, assuming that one can have constraints with friction too; the results thus

obtained will be then used to the study of some particular problems (the motion of the

gyroscope in contact with a fixed plane, the motion of a heavy circular disc or of a

heavy sphere on a fixed plane etc.).

The first study in this direction has been made by S.-D. Poisson (the motion of a

heavy rigid solid in contact with a fixed plane); Cournot took again the problem

considering the friction too. The particular case of the motion of a billiard ball has been

considered by Coriolis in 1835. Puiseux studied the motion of a heavy rigid solid of

rotation on a perfectly smooth horizontal plane; Slesser tackled in 1861 the same case,

assuming that the rigid solid can roll and pivot without sliding, Neumann taking again

the problem in 1886. Other results are due to Scouten, Ferrers, Carvallo, Korteweg and

Appell.

17.1.2.1 General Considerations

Let be two rigid solids

S and

′

S , bounded by the surfaces S and

′

, respectively,

having – at every moment – the ordinary common point

′

≡PP

, ∈PS,

′′

∈PS

(obviously, the points

P and

′

of the two rigid solids are always other ones, the

mentioned situation being instantaneous), at which they have the same tangent plane

1 ; the distribution of the velocities in the relative motion of a rigid solid with respect

to another one has been considered in Chap. 5, Sect. 3.3.1. In this study, we neglect any

interaction which can intervene between the two solids, excepting the actions of

contact. The condition of impenetrability of the rigid solids (which can be separated or

in contact) is expressed, in general by an inequality; e.g., if the rigid solids are two

spheres

()

,OR and

()

′′

,OR

, the unilateral constraint relation is expressed in the form

OO R R

′′

≥+

JJJG

. We assume, in what follows, that the constraints are bilateral, having

contact relations at one point

′

≡PP

, expressed by equalities.

Let R be the constraint force which represents the action of the rigid solid

′

S upon

the rigid solid

S, at the point P , and let

′

R be the constraint force corresponding to

17 Dynamics of Systems of Rigid Solids

471

the action of a rigid solid

S upon the rigid solid

′

S , at the point

′

; in conformity to

the theorem of action and reaction, these forces verify the relation

′

RR0. We

mention that the equations of motion of the rigid solid (the theorems of momentum and

of moment of momentum), the theorem of action and reaction and the relation of

impenetrability (relation of bilateral constraint) are not sufficient to determine the

unknowns which intervene (as a matter of fact, the constraint forces R and

′

R are

unknowns); to solve the problem, one must add some supplementary conditions.

In case of a contact without friction (the surfaces

S and S

′

are smooth), the

constraint forces R and

′

R must be normal to the tangent plane 1 at the point of

contact, being denoted by N and

′

N respectively (we have

′

NN 0; eventual

tangential components T and

′

T would correspond to an infinite relative displacement

in the plane

1 . We notice that these constraint forces are pressures, the sense of which

is towards the interior of the rigid solid upon which they act and which vanish when the

contact ceases (see Chap. 3, Sect. 2.2.9 too). In some cases, a contact takes place along

a curve or on a certain surface and one can make analogous considerations.

If the contact is with friction, remaining punctual, then the friction is a sliding

friction. We can decompose the constraint force in the form

=+RNT (the same for

the constraint force

′

R ) where N is the ideal constraint force (normal, without friction),

while T is the sliding constraint force (see Chap. 3, Sect.. 2.2.12 too). We denote by

the Coulombian coefficient of friction ( 0f ≥ ), introduced in Chap. 3, Sect.. 2.2.11.

Further, we assume that the rigid solid

′

S is at rest with respect to an inertial frame of

reference, studying the motion of the rigid solid

S on the surface

′

. If the sliding

velocity of the rigid solid

S on the surface

′

at the contact point (the velocity of a

point

Q which coincides with

′

≡PP

at any moment t, hence the velocity of

transportation with respect to the surface

′

, contained in the plane 1 and given by

(5.3.21)) vanishes (

=v0), then we have f≤TN; to

≠v0 corresponds

f=TN, with

M=−Tv, /0

fM =>Nv (in this limit case, the vector R

has its support along a generatrix of the cone of friction).

In fact, in the dynamic case one uses the Coulomb-Morin relation in the form

vers

fN=−Tv, (17.1.14)

where

is a coefficient of a dynamic friction; we notice that

≤

, =

ff, where

f is the coefficient of static friction. In general, we can have ()

ffv= .

The equation of motion of the theoretical contact point

P is of the form

MfN=−



τ ,

(17.1.15)

where F is the resultant of the given forces, while M is the mass of the rigid solid

mathematically modelled as a particle (considered to be reduced to the point

P); by

integration, we get

MECHANICAL SYSTEMS, CLASSICAL MODELS

472

Mv h f N s=+ ⋅ −

³³

Fr ,

(17.1.16)

where

[

]

∈ 0,ss

is a curvilinear co-ordinate along the trajectory of the point P. In case

of a conservative force, we can write

TV h fNs+=−

(17.1.16')

where

h is the energy constant. Because the above integral is always positive, it results

a decrease of the mechanical energy of the rigid solid

S which slides on the surface of

another fixed rigid solid

′

S . This energy is lost, being transformed in a degraded

energy (e.g., heat).

But, practically, the contact between rigid solids is not punctual taking place on a

small part 4 of the surface, where a process of deformation takes place (the model of

rigid is only an approximation); the actions

R of a solid upon the other one are

distributed on 4after a unknown law (as a mater fact, even the surface 4 is, in general,

difficult to specify). Therefore, assuming some simplifying hypotheses, the torsor of

these actions at a point

′

≡∈PP

4 is determined.

We assume, further, the rigid model for the two solids, the contact taking place –

theoretically – at the point

′

≡PP

; the action of a solid upon the other will be

modelled by a torsor (a force and a moment (couple)), applied at the theoretical point of

contact, the theorem of action and reaction being used. If we suppose, further, that the

rigid solid

′

S is at rest with respect to an inertial frame of reference

′

, at the point

P of the solid S will act, in general, a constraint torsor

{

}

τ R

of resultant R and

resultant moment

M (see Chap. 3, Sect.. 2.2.12 too). We effect a decomposition, so

that one component be along the normal to the surface

S at P, the other component

being contained in the plane

1 tangent to this surface, at the same point; one obtains

thus

=+RNT and

=+MMM where

M is the pivoting friction moment

(along the normal), while

M is the rolling friction moment (in the tangent plane). As

well, we notice that the motion of the rigid solid

S with respect to the surface S

′

characterized by a translation of velocity

()

and by a rotation of angular velocity

()tω (see Chap. 5, Sect.. 3.3.1 too); analogously, we decompose the angular velocity in

the form

=+ω ω ω , where ()

tω is the pivoting angular velocity, while ()

tω is

the rolling angular velocity. If the rigid solid

S is at rest with respect to the frame of

reference

′

(

=v0, = 0ω ), then the inequalities

TfN≤ ,

MsN≤ ,

MaN≤ , ,, 0

sa≥ , (17.1.17)

take place, where

f is the (non-dimensional) coefficient of sliding friction, s is the

rolling friction coefficient, while

a is the pivoting coefficient of friction (s and a have

the dimension of a length), as it has been shown in detail in Chap. 5, Sect.. 3.3.1. In the

17 Dynamics of Systems of Rigid Solids

473