Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

One obtains

()vvt= and then ()

ft= , the consumption of mass being thus

determined.

16.3.2.3 Considerations Concerning the Motion of the Rocket

In the case of a rocket launched along the ascendent vertical, Meshcherskiĭ’s equation

(see Chap. 10, Sect. 3.1.2 too) reads

(, ) 0mv mg Q v x mw++ + =



(16.3.17)

where

=−wuv is the relative velocity of the evacuated masses, while vx=  . It is

assumed that: (i)

constg = for relatively small heights (100...200 km) from the

Earth’s surface; (ii)

constw = , hence a constant emission of mass; (iii) the influence

of the mass variation in the resistance of the air, characterized by the function

ϕ, is

neglected; (iv) the variation of the momentum in the interior of the rocket, modelled as

a particle, is neglected; (v) the influence of the motion of rotation of the Earth is not

taken into consideration. The conditions

0x = ,

vv= ,

mm= at the initial moment

0t = and

xx= ,

vv= ,

mm= at a certain moment

tt= being given, G.

Hamel, in 1936, put the problem to determine the minimal initial mass

so that the

rocket reach a given altitude

x (at the end of the active segment (

tt= ) for which we

have the velocity

v and the mass

m ).

Noting that

() ()mt mf t= , (0) 1

= , and applying the formula (10.3.13") for an

equation of the form (10.3.13), (10.3.13'), we get

[]

{}

[

]

[]

{}

{

}

0 0

()/d ()/d

()()

eed

t t

gvt w t gv w

Qvtxt

mm t

ττ−+ −+

∫∫

=−

∫



where we took into consideration also the initial condition

(0)mm= ; after

calculations, we can write

[]

()

/()//

e()()ede

vw gtvt w gtv w

mQvtxttm

∫

111

(, ;)d ( , )

Fvxt t F v t=+

∫

(16.3.18)

obtaining a relation between the mechanical quantities at the end of the active segment.

After the consumption of the combustible, due to the existent kinetic energy, the

rocket continues to ascend, in conformity to the equation of motion

(, ) 0mv mg Q vx++ =



(16.3.19)

which is obtained from (16.3.17), making

0m =

and taking

mm= ; this equation is

of the form

(, ;) (;) 0Fvxt F vt+=



and can also be written in the form

16 Other Considerations on the Dynamics of the Rigid Solid

443

(, )

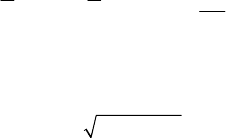
vv Q v x

′

= ,

(, ) (, )Qvx Qvx g

⎡

⎤

=− +

⎢

⎥

⎣

⎦

(16.3.19')

Assuming that

(, )Qvx mg and integrating, we get

() 2( )vx ghxψ== −,

[

]

,xxh∈ ,

(16.3.20)

hence a formula of Torricelli type, where

() 0hψ = . In this case,

()vxψ= and

111 1 1 1

(,) ((),)Fvt F x tψ= .

In the variational problem which is put (the minimizing of the functional (16.3.18))

one takes, usually,

x and

t fixed, to avoid the difficulties of calculation, writing –

consequently – the Euler-Lagrange equation for the function

(, ;)Fvxt ; if

x and

are variable, then the problem becomes much more complicated.

16.3.3 The Motion of the Aircraft Fitted Out with Jet

Propulsion Motors

In the case of modern aircraft fitted out with systems of jet propulsion of great traction,

a great consumption of combustible is emphasized; thus, during the work of the system

of propulsion, in the body of the aircraft circulate great masses of liquid, air and gases.

To determine the equations of motion which allow the study of the flying qualities, it is

necessary to take into account the displacement of the mass centre of the aircraft, the

variation of the moments of inertia and of the non-inertial frame of reference of the

principal axes of inertia with respect to a frame rigidly linked to the outer covering of

the aircraft. In 1975, M.M. Niţă and Gh. Drăgănoiu dealt with the motion of the mass

centre of the aircraft, while M.M. Niţă, considered, in 1979, its motion about the res-

pective centre; in this case, it is necessary that the aircraft be modelled as a mechanical

system of variable mass, by simultaneous emission and capture of mass (gas and air,

respectively). In what follows, we make some general considerations concerning the

general theorems corresponding to the mentioned case, applying then these results to

the motion of the aircraft.

16.3.3.1 Theorems of Momentum and of Moment of Momentum

We assume that the aircraft (modelled as a mechanical system S of variable mass) the

motion of which we are studying has, at the moment

t, a mass M (contained in the

interior of a surface

Σ, corresponding to the outer covering of the aircraft) of the form

scg

MM M M=++, (16.3.21)

where

M is the solid mass,

M is the combustible mass and

M is the mass of the

particles of gas (air or combustion products); the position vector of the mass centre

of the mechanical system

S, with respect to a non-inertial frame of reference R of

MECHANICAL SYSTEMS, CLASSICAL MODELS

444

axes

123

Ox x x , rigidly connected to the outer covering of the aircraft (O is a point of the

outer covering), is given by

()

ss cc gg

MMM

=++

ρρρρ

(16.3.21')

where

scg

ρρρ

are the position vectors of the mass centres corresponding to the solid

part, to the liquid combustible and to the particles of gas, respectively. The velocity of

the centre

C, relative to the frame of reference R, is given by

()

cccgg

MMM

tMt t

∂∂ ∂

⎡

⎤

== + −

⎢

⎥

∂∂ ∂

⎣

⎦



ρρρ

(16.3.21'')

the derivative of the mass with respect to time being independent on the frame and

having obviously,

M =



and /

t∂∂=0

We can take

MVVμμ

∑∑

∫∫∫ ∫∫∫

(16.3.22)

where

μ is the density of the liquid combustible, while

V and

V represent the

volume of a room (bunker, tubing etc.) occupied by the liquid at a moment

t, the indices

j and i specifying the p commuted and the q non-commuted rooms respectively, in the

consumption circuit. These integrals are defined on variable domains, so that, by the

displacements of the free surfaces

S and

, corresponding to the above mentioned

volumes, respectively, it results

()d ()d

ll ll

MSSμμ

=⋅+⋅

∑∑

∫∫ ∫∫



wn wn

;

(16.3.22')

it has been assumed that the liquid is incompressible and that

w is the relative velocity

with respect to the frame of reference

R of a particle on the free surface, n being the

unit vector of the external normal to this surface; obviously, the integrals corresponding

to the

q components non-commuted to the consumption circuit vanish. Analogously,

ga g

MVVμμ=+

∫∫∫ ∫∫∫

(16.3.23)

where by

μ and

μ have been denoted the densities of the air and of the gas,

respectively,

V and

V , being the corresponding volumes; noting that const

V =

and

const

V = , it results

16 Other Considerations on the Dynamics of the Rigid Solid

445

ga g

MVVμμ=+

∫∫∫ ∫∫∫





(16.3.23')

Returning to the relation (16.3.22'), we notice that the first integral represents, in

absolute value, the mass of the liquid contained in the volume delivered by the

displacement of the free surface

S in a unit of time and which, on the basis of the

continuity condition, is equal to the rate of flow of the liquid combustible

Q in the

room

V ; hence,

()d

SQμ ⋅=−

∫∫

wn ,

MQQ

=− =−

∑



(16.3.24)

where

Q is the total rate of flow of the liquid combustible. Noting that

ll ll

MVVμμ

∑∑

∫∫∫ ∫∫∫

rrρ ,

it results

() d

lL l l

MQ V

∂∂

=− +

∂∂

∑

∫∫∫

rρρ ,

(16.3.24')

where

∑

ρρ

()d

ll l

⋅

∫∫

rwn

ρ ,

(16.3.24'')

r being the position vector of a particle of liquid of the free surface, with respect to the

frame of reference

R. The vector

specifies the position of the mass centre of the

mass of combustible contained in the volume delivered by the displacement of the free

surface in a unit time; if the product

()

μ ⋅wn is the same at all the points of the

surface

S , then the vector

defines the centre of mass of this surface, while the

vector

corresponds to the mass centre of all free surfaces in the rooms commuted in

the consumption circuit.

Vμ

∫∫∫

r is the static moment of the system of particles of liquid combustible

contained in the volume

V relative to the rooms commuted in the consumption circuit

and if we take into account the formula (A.2.80'), then we get the momentum with

respect to the non-inertial frame of reference

R in the form

d()d

ll ll l

VSμμ+⋅

∫∫∫ ∫∫



rrwn

, where S is the surface which bounds the domain of

MECHANICAL SYSTEMS, CLASSICAL MODELS

446

volume

V. In connection with these rooms, we consider the mixing surfaces

1,2,...,kr= , through which passes the liquid combustible, leaving the considered

system (one assumes that, at the points of these surfaces, takes place the mixing of the

particles of liquid with the particles of air or gas – at the systems with post-combustion–

and the instantaneous transformation of this mixture in gas). Noting that



, the

momentum of the mentioned liquid combustible is given by

()d ( )d ( )

ll l ll M L

SSQμμ

⋅+ ⋅= −

∑∑

∫∫ ∫∫

rwn rwn

ρρ

where

∑

ρρ

()d

⋅

∫∫

rwn

(16.3.25)

with an analogous significance concerning the surfaces of mixing

w being the

relative velocity of a particle of liquid on this surface, in the frame of reference

obviously, we have

QQQ

∑

, ()d

QSμ=⋅

∫∫

rwn ,

(16.3.25')

where

Q is the rate of flow of the combustible which passes through the surface

S ,

being transformed in gas. The relative momentum of the system of particles of liquid

combustible contained in the rooms non-commuted to the consumption circuit is given

by the second term in (16.3.24'); in this case, the momentum of the system of particles,

corresponding to all the rooms, will be expressed in the form

() d

lML ll

∂

=−+

∂

∑

∫∫∫

H ρρ ρ ,

(16.3.25'')

while the formula (16.3.24') becomes

()

cc c

∂

=−

∂

ρρ

(16.3.26)

where we took into account (16.3.25").

In what concerns the mass of the gas particles (air or combustion products) we can

make analogous considerations. Thus, the condition of continuity of the air flow is

given by

mem

VQ Qμ =−

∫∫∫



(16.3.27)

16 Other Considerations on the Dynamics of the Rigid Solid

447

where

Q is the rate of flow of the air at the entrance sections

, 1,2,.....,

hn= ,

while

is the rate of flow of the air at the passing through the mixing surfaces; we

have

()d

ee ma

QQ Sμ

==− ⋅

∑∑

∫∫

wn ,

()d

mm ma

QQ Sμ

== ⋅

∑∑

∫∫

wn,

(16.3.27')

where

and

represent the velocities of a particle of air at the section of entrance

and at the section of mixing, respectively. The condition of continuity of the flow of

gases is of the form

d()d()d0

ggg gg

VS S

VSSμμ μ

+⋅+⋅=

∑∑

∫∫∫ ∫∫ ∫∫



wn wn

where

w and

w are the velocities of a particle of gas at the surface of mixing and at

the surface of exit (issue)

S , 1,2,...,

ln= , respectively. Assuming that, at the passing

through the surfaces of mixing, the liquid is transformed instantaneously in gas, this

condition becomes

gcm

VQ Q Qμ =+ −

∫∫



(16.3.28)

with

()d( )

gg m

SQQμ

⋅=−+

∑

∫∫

wn ,

()d

QQ Sμ

== ⋅

∑∑

∫∫

(16.3.28')

Q being the rate of flow of gases at the sections of exit.

From (16.3.23'), (16.3.27) and (16.3.28) , it results

gce

MQQQ=+−



(16.3.29)

Noting that

MQ=−



(16.3.29')

from (16.3.24) and (16.3.25'), the relation (16.3.21) leads to

MQ Q=−



(16.3.30)

MECHANICAL SYSTEMS, CLASSICAL MODELS

448

because

M =



. If 0

μμ==



and if we take into account the relation (16.3.27)

(which leads to

QQ= ) and the relation (16.3.28) (wherefrom

QQ Q=+), then

it results

MQ=−



(16.3.30')

Using the relations (16.3.27'), (16.3.28') and (16.3.30),

the formula (13.2.12) allows

to express the theorem of momentum, in the case of the considered problems, in the

form

()d ()d

aa a gg g

μμ

′

+⋅+⋅=

∑∑

∫∫ ∫∫

uwn uwn R

(16.3.31)

where

′

H is the momentum of the mechanical system S with respect to an inertial

frame of reference

u and

u are the velocities of the particles of air at the

surface of entrance and of the particles of gas at the surface of exit, respectively, with

respect to the same frame, while

R is the resultant of the given external forces. As well,

in conformity to the formula (13.2.15), extended to the generalized equation of

Meshcherskiĭ, the theorem of moment of momentum for the above problem is given by

()d ()d

aaaa gggg

μμ

′

′′

+× ⋅+× ⋅=

∑∑

∫∫ ∫∫

ru w n ru wn M

(16.3.32)

where

′

K is the moment of momentum of the system S with respect to the inertial

frame of reference,

′

r and

′

r are the position vectors of the particles of air at the

surface of entrance and of the particles of gas at the section of exit, respectively, with

respect to the same frame, while

′

M is the resultant moment of the given external

forces with respect to the pole

′

of the respective frame.

Obviously, starting from the results given in Sect. 13.2.1.2, we can give also other

remarkable forms to these theorems.

16.3.3.2 Motion of the Centre of Mass

The mass centre of the particles of gas is given by the relation of static moments

gg a a g g

MVVμμ=+

∫∫∫ ∫∫∫

rrρ ,

(16.3.33)

where

and

r are the position vectors of the particles of air and of gas, respectively,

with respect to the frame of reference

R; thus, it results

() d d

gg a a g g

MVV

μμ

∂

∫∫∫ ∫∫∫



rrρ

16 Other Considerations on the Dynamics of the Rigid Solid

449

As in the case of particles of liquid, we can write the momentum of the mass of the

particles of air and of the particles of gas, respectively, with respect to the frame

R, in

the form

d()d()d

ae m

aaa aaa aaa

VS S

VS Sμμ μ

=+ ⋅+ ⋅

∑∑

∫∫∫ ∫∫ ∫∫



Hr rwn rwn,

d()d()d

ggg ggg ggg

VS S

VSSμμ μ

=+ ⋅+ ⋅

∑∑

∫∫∫ ∫∫ ∫∫

Hr rwn rwn.

(16.3.34)

If the densities

μμ and

μ , as well as the scalar products

⋅wn,

⋅wn and

⋅wn are uniformly distributed on the mixing surface

S , then we can write

()d ()d

aa a gg g c

SSQμμ⋅+ ⋅=−

∫∫ ∫∫

rwn rwn

Introducing the notations

∑

ρρ

∑

ρρ

()d

aa a

⋅

∫∫

rwn

()d

gg g

⋅

∫∫

rwn

(16.3.35)

where

E and I represent the centre of the sections of entrance and the centre of the

sections of exit (issue), respectively, the relations (16.3.27'), (16.3.28'), (16.3.33)-

(16.3.35) lead to

()

gg a g c e

MEI

MQQQ

∂

=++ + −

∂

rHH

ρρρ

(16.3.36)

If the products

()

μ ⋅wn and ()

μ ⋅wn are the same for all the points of the

sections

S and

S , respectively, then the vectors

and

define the mass centres

of these sections, while the points

E and I represent the mass centres of the sections of

entrance and exit, respectively. Taking into account

the relations (16.3.26), (16.3.30),

(16.3.36), the relation (16.3.21) allows to express the velocity of the mass centre

C of

the mechanical system

S with respect to the frame of reference R in the form

[]

()()

CEI

∂

== + −− −

∂

ρρ ρρ

(16.3.37)

where

=++HH H H

(16.3.38)

is the momentum of this mechanical system with respect to the same frame.

MECHANICAL SYSTEMS, CLASSICAL MODELS

450

In the case of the aircraft fitted with rocket motors we have

Q =

, so that

[]

()

=−−wH

ρρ

(16.3.37')

Let

′

=− = +×

vuwv rω be the velocity of a point of the outer covering of the

aircraft, hence of the non-inertial frame of reference

R with respect to the inertial

frame

′

R (velocity of transportation), where

′

v is the velocity of the pole O with

respect to the frame

′

R , while ω is the rotation angular velocity of the frame R with

respect to the same frame

′

. The theorem of momentum (16.3.31) may be written

also in the form

hh ll

ee e

ii i

QQ QQ

′

−−++=

∑∑

wv wvR

(16.3.39)

where we took into account the relations ( 16.3.27'), (16.3.28'), (16.3.35) and where

w ,

w are the velocities relative to the frame R, considered to be constant, at the

section of entrance

and at the section of exit

S , respectively,

v and

v being the

velocities of transportation of the centres

E and I, respectively, given by the relations

()d ()d

ee e

aa a a a

SSμμ

′

⋅= ⋅

∑∑

∫∫ ∫∫

vwn v wn

()d( )

aa a e e

OE E

SQQμ

′

+× ⋅ =− + × =−

∑

∫∫

rwn v vωωρ,

()d ()d

ii i

gg g g g

SSμμ

′

⋅= ⋅

∑∑

∫∫ ∫∫

vwn v wn

()d( )

gg g

OI I

SQQμ

′

+× ⋅ =− + × =

∑

∫∫

rwn v vωωρ

Taking into account (16.2.21), we can write

scg

′′′′

=++

HHHH, so that

ddd

dddd

tttt

′

′′′

=++

HHH

(16.3.40)

We have

ss s

′

==Hu v, because the velocity relative to R of the mass

centre of the solid part vanishes (

=w0); hence,

′

(16.3.41)

where

′

is the acceleration of transportation of the mass centre of the solid part.

Calculating the momentum in the motion of transportation in the form

16 Other Considerations on the Dynamics of the Rigid Solid

451

11 11

dd dd

j j

i i

ll ll

pq pq

llOll

VV VV

ji ji

VV VVμμ μμ

== ==

⎛⎞

′

+= +

⎜⎟

⎝⎠

∑∑ ∑∑

∫∫∫ ∫∫∫ ∫∫∫ ∫∫∫

vvv

ll ll

VVμμ

⎛⎞

+× +

⎜⎟

⎝⎠

∑∑

∫∫∫ ∫∫∫

rrω ,

corresponding to the liquid combustible in the rooms occupied by it at the moment

t, we

can write (

is the momentum of the liquid part relative to the frame of reference R)

()

cc c

′′

=+ +×HH vω

(16.3.42)

where we took into account (16.3.22) and the relation which gives the corresponding

centre of mass. Taking into account (16.3.26), we get

lM C

′

∂

′

= +×− +

∂

Hv a

(16.3.43)

where

v is the velocity of transportation of the centre M of the mixing surfaces,

′

is the acceleration of transportation of the centre of mass of the combustible, while the

operator

/ t∂∂ corresponds to the derivative with respect to the frame R.

Starting from (16.3.23),

it results, analogously,

()

ggg g

′′

=+ +×HH vω

(16.3.44)

for the particles gas-air. We obtain thus (

′

is the acceleration of transportation of the

mass centre the gas-air part)

gc e g

MEI C

QQQM

′

∂

′

=+×+ + −+

∂

Hv vv a

(16.3.45)

where we took into account (16.3.29), (16.3.36) and the manner of introduction of the

velocities of transportation

v and

v .

Noting that at a fixed moment we can write

sc g

scg

CC C C

MM M M

′′ ′ ′

=++aa a a

(16.3.46)

where

′

a is the acceleration of transportation of the mass centre of the mechanical

system

S, and denoting by

=+HH H the momentum of this system with respect

to the frame of reference

R (the relative momentum of the solid part vanishes), the

theorem of momentum (16.3.39), with (16.3.40), leads to

hh ll

MQQ

∂

′

=+ − − − ×

∂

∑∑

aR w w H

ω .

(16.3.47)

MECHANICAL SYSTEMS, CLASSICAL MODELS

452