Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

case in which a sliding, a rolling and a pivoting of the rigid solid

S on the surface

′

take place (

≠v0,

≠ 0ω ,

≠ 0ω ), the inequalities (17.1.17) are replaced by

equalities, in the form

M=−Tv,

M=−M ω ,

ppn

M=−M ω ,

, 0

=>, 0

(17.1.17')

If one or two of the types of motion mentioned above do not take place, then the

corresponding relations of equality (17.1.17') are replaced by the inequalities (17.1.17),

which put in evidence the respective friction phenomena. E.g., if

≠v0,

==0ω ω , then we have a (pure) sliding without rolling and pivoting (the surfaces

S and

′

are perfectly smooth), while if

=v0,

≠ 0ω ,

= 0ω , then we have a

(pure) rolling without sliding and pivoting (the surfaces

S and

′

are perfectly rough).

We have assumed, in the above considerations, that the friction coefficients

f, s and a

are the same both in the static (relations (17.1.17)) and in the dynamic case (relations

(17.1.17')).

If one has a contact at several points between the surfaces

S and

′

, then at one of

these points (let be the point

P ) is concentrated the contribution due to the constraint

forces et each point. As well, if between these surfaces takes place a contact along an

arc of curve

C, then one considers the constraint corresponding to an element ds of the

curve, the constraint forces being in direct proportion to this element; the contribution

of all these constraints is obtained calculating the corresponding torsor by integration

along the arc of curve

C. In general, if the surfaces S and

′

have in common a part 4

of the surface, so that

∈P 4

, the constraint forces are in direct proportion to the

element of area d4, while

ddd444=+RNT, ddd

444=+MMM; the

torsor of these forces is

{}

{

}

d, d

44τ=

³³ ³³

RRM, where R and

are

vector functions.

We assume now that also the rigid solid

′

(hence, the surface

′

too) is in motion

with respect to the inertial frame of reference

′

. In this case, the velocity of the point

Q, which coincides with

′

≡PP

at any moment t , with respect to this frame, is given

QP P

′′

=+ = +vvwvw where

w and

′

w , are the velocities of these points

with respect to the rigid solids

S and

′

, respectively, and one can write

()

′′

−=−−vv ww; because the second difference is contained in the common

tangent plane

1 , the difference

′

−vv has the same property. As well, if ω and

′

are the instantaneous rotations of the rigid solid

S and

′

, respectively, with respect

to the frame of reference

′

, then

′

ω − ω

is the instantaneous rotation of the rigid

solid

S relative to the rigid solid

′

S . The forces of friction exerted by

′

upon S

are expressed also by the torsor

{

}

τ R , which is decomposed analogously, being

MECHANICAL SYSTEMS, CLASSICAL MODELS

474

led to the same inequalities (17.1.17). If a relative sliding, rolling and pivoting takes

place, then the relations (17.1.17') read

()

′

=− −Tvv,

()

′

=− −M ω ω ,

()

ppnn

′

=− −M ω ω , ,, 0

MM M > ,

(17.1.18)

where we have put in evidence the tangential and the normal components of the angular

velocities. Corresponding to the theorem of action and reaction, the rigid solid

S acts

upon the rigid solid

′

by forces the torsor of which is

{

}

′′

RM , so that

′

RR 0,

′

MM 0; as well, the decompositions

′′′

RNT,

′′′

MMM,

′

NN 0,

′

TT 0,

′

MM 0,

′

MM 0 take

place too.

The formula (14.1.37) allows to express the elementary work of the forces which rise

on the contact surface 4 of the rigid solids

S and

′

in the form

()

ddd

Wt t

′′

′′′

=⋅+ ⋅ + ⋅ + ⋅

Rv M R v Mω ω

()

[

]

′

=⋅ − + ⋅

Rv v M ω − ω ;

(17.1.19)

one can notice that this work corresponds to the motion of the rigid solid

S with

respect to the rigid solid

′

. Decomposing R,

M and ω so as to obtain the normal

and the tangential components and observing that

()

′

⋅− =Nv v (the difference

′

−vv is contained in the plane 1 ),

()

-0

′

⋅=

M ω ω ,

()

-0

rnn

′

⋅=

M ω ω ,

it results

()

()( )

[

]

rpnn

′

′′′

=⋅ − + ⋅ − + ⋅ −

MTv v M ω ω ω ω

()

()( )

rpnn

tMMM

′

′′

ªº

=− − + − + − <

¬¼

ω ω ω ω ,

(17.1.19')

where we took into account the relations (17.1.18). Hence, the elementary work of the

friction forces in case of the contact of two rigid solids is negative. Taking into account

the formula (14.1.37), we get the power of these forces in the form

()

′

′′

=⋅ − + ⋅ −

ω ωRv v M ,

(17.1.19'')

quantity which – obviously – is negative too.

We mention that, in a first approximation, the effect of the couples of rolling and

pivoting can be neglected.

17.1.2.2 Painlevé’s Paradox

Painlevé called attention to some contradictions in the study of the motion of a non-

homogeneous heavy circular disc, which moves in a vertical plane, laying on a fixed

rough horizontal straight line; thus, the motion is a plane-parallel one (see Sect. 14.2.2.7

too). Let be thus a non-homogeneous disc of centre

O, radius R and weight Mg, the

centre of gravity of which is at

C, of position vector ρ with respect to a movable frame

17 Dynamics of Systems of Rigid Solids

475

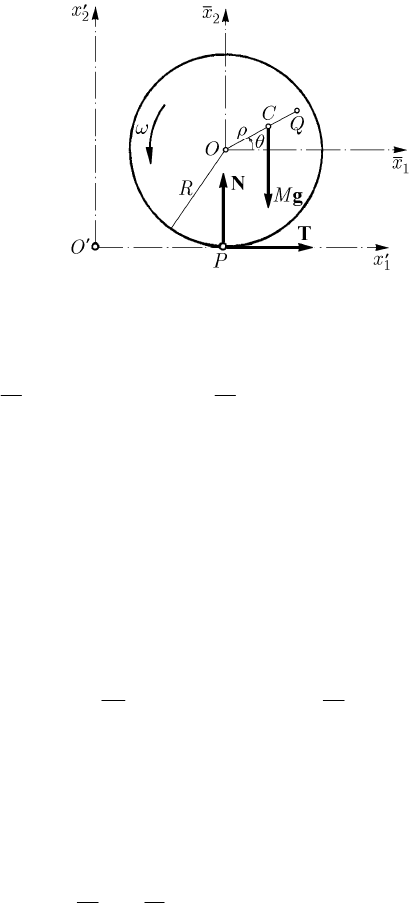
of reference

R of axes

Ox x

parallel to those of a fixed frame

′

of axes

′′′

Ox x ,

the horizontal axis

′′

Ox being tangent to the disc (Fig. 17.6). At the point of contact P

act the normal constraint force

N and the sliding friction force T. The velocity of the

point

C with respect to the frame

′

is given by

′′

+×

v=v ω

, where the

angular velocity

ω corresponds to a positive rotation.

Fig. 17.6 Painlevé’s paradox

The theorem of motion of the mass centre gives the equation of motion

()

Mv T

′

−=,

()

MNMg

XS =−

(17.1.20)

As well, the theorem of moment of momentum with respect to a frame of Koenig leads

()

IRTNXSS=+ −



(17.1.20')

where

IMi

is the central moment of inertia with respect to an axis parallel to the

′′

Ox -axis, while

i is the corresponding radius of the gyration.

Eliminating



between the second equation (17.1.20) and (17.1.20'), we get (we

mention that

()

==−=−

dcos/d sintSSR SRRXS



)

()

[]

221

RTN g

SX S S−+ + − −+=

a relation which must take place at the initial moment too. We assume that at this

moment

SS, =

0S , the centre C being on the

Ox -axis; as well, we take

and we consider that 0

′

< , so that =TfN (we have

0N >

). Hence, at

the initial moment, the relation

()

fR g

ªº

−−=

«»

¬¼

(17.1.21)

MECHANICAL SYSTEMS, CLASSICAL MODELS

476

must take place.

Assuming that the non-homogeneity is obtained by attaching to a homogeneous disc

of radius

R and mass

M a second homogeneous disc of radius r and mass

M at the

point

Q, situated at the distance a from the centre O, the relation of static moments

gives

()

Ma MSS−= ; with the aid of the non-dimensional ratio =

MMF it

results

[

]

/(1 ) aSF F=+. According to the Huygens – Steiner theorem (formula

(3.1.113)), we may write

()

=+++−

ªº

¬¼

222 2

/2 /2

Mi M R M r aSS,

wherefrom

()

{

}

2222

12 1

iRra

=++

We obtain thus the ratio

()

()()

()

() ()

222

1/ /

11/ 2/

faR aR

rR aR

ISF

+−

=−=

ªº

++ +

¬¼

. (17.1.21')

We observe that one can find a technical solution so that the subunitary non-

dimensional ratio

/rR be sufficiently small, the subunitary non-dimensional ratio

/aR be close to 1/2, the coefficient of sliding friction be sufficiently great, while the

non-dimensional ratio F be superunitary, sufficiently great, so that

1I > . In this case, it

results from (17.1.21) that one must have

0N < , contradicting thus the Coulombian

model of sliding friction.

F. Klein showed later that the motion considered by Painlevé does not satisfy the

continuity hypotheses assumed in the Newtonian modelling of mechanics relative to the

initial conditions. As a matter of fact, at the initial moment intervenes an impulse which

modifies the static laws assumed for the friction, the deterministic aspect of mechanics

being thus preserved.

17.1.2.3 Motion of a Rigid Solid Which Slides Frictionless on a Fixed Plane

Let us consider a rigid solid S, bounded by the surface S, which slides without friction

on a fixed plane

P, remaining during the motion in contact to this one. We assume that

the fixed frame of reference

′

has the axes

′′

Ox and

′′

Ox contained in this plane,

the

′′

Ox -axis being normal to the plane and directed towards the part in which is the

rigid solid

S ; as well, we introduce the movable frame of reference R, having the

pole at the mass centre

C of the solid and being rigidly linked to it, and the movable

frame

R , with the pole at the same point and the axes parallel to the axes of the frame

′

. To specify the position of the rigid solid S, we determine the position of the

mass

C (three parameters

′′′

123

,,SSS) and the three angles Z, R and K of Euler (three

parameters), which give the position of the frame

R with respect to the frame R . But

these six parameters are not independent.

17 Dynamics of Systems of Rigid Solids

477

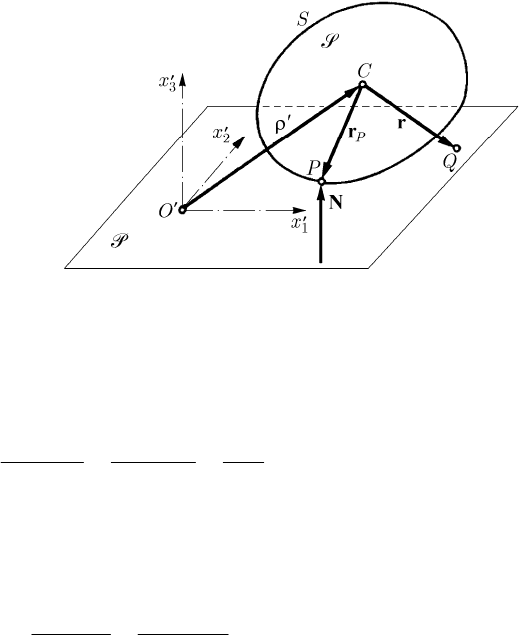
Indeed, let

()

123

,, 0fxx x be the equation of the surface S with respect to the

frame of reference

R, while

r and r are the position vectors corresponding to the

contact point

P and to an arbitrary point Q of the plane P (Fig. 17.7), respectively; the

equation of this plane is written in the form

()

grad 0

f−⋅ =rr .

(17.1.22)

Fig. 17.7 Motion of a rigid solid which slides frictionless on a fixed plane

The rigid solid

S being tangent to the plane P, there must exist a point

()

∈

123

,,xxx S at which the tangent plane be normal to

()

sin sin , sin cos , cosRK RK R

′

i , and the relations

()

,1 ,2 ,3

123

,,;,,

sin sin sin cos cos

fff

xxx

'ZRK

RK R K R

===

(17.1.23)

take place. As well, this tangent plane must pass through the pole

′

, so that we must

have

sin sinx RK

′

⋅= +ri

′

+=−

233

sin cos cosxxRK R S. The relations (17.1.23)

read

()

123

grad

,,;,,

xxx

'ZRK

⋅

′′

⋅−

(17.1.23')

Eliminating

123

,,xxx between the equations (17.1.23), (17.1.23') and taking into

account the equation of the surface

S, we find a relation of the form

()

,,SSZRK

′′

= ,

(17.1.24)

which is – in fact – the constraint relation of the rigid solid

S ; hence, only five

independent parameters are necessary to specify the motion, the rigid solid

S having

only five degrees of freedom.

MECHANICAL SYSTEMS, CLASSICAL MODELS

478

The theorem of motion of the mass centre, in projection on the

′′

Ox -axes,

= 1, 2, 3j , reads

′

=⋅

Ri, 1, 2B = ,

′

=⋅+

Ri ,

(17.1.25)

where

R is the resultant of the given forces which act upon the rigid solid S ; the

constraint force

N at the contact point P is normal to the plane P, having thus only one

component

N along the

′′

Ox -axis, which is given by the third equation (17.1.25). The

theorem of moment of momentum written in the frame

R with respect to the movable

axis

Cx leads to Euler’s equation

()

+− =

33 2 1 12

III MXXX



(17.1.26)

where

M is the projection on

Cx of the moment with respect to C of the given

forces and where we notice that the moment of the constraint force

R has not a non-

zero component along this axis; as well, projecting the equation given by the theorem

of moment of momentum on the

Cx -axis (of fixed direction) and noting that

()

[

]

()

[

]

d/d d /d

′′

⋅= ⋅ω ωIiIi, we may write

()

11 22 33

sin sin sin cos cos

II IM

XRKXRK X R

′

++=,

(17.1.26')

where we have introduced the moment of the given forces with respect to this axis.

Taking into account the results in Sects. 14.1.1.6 and 14.1.1.7, we can write the theorem

of kinetic energy in the form

()

222

11 22 3 3

2d 2

MIII

XXX

′

ªº

§·

′

+++=⋅

¨¸

«»

©¹

¬¼

R .

(17.1.27)

We obtain thus five scalar equations, which do not contain the unknown constraint

force

N, to determine the five independent parameters characterizing the motion of the

rigid solid

S .

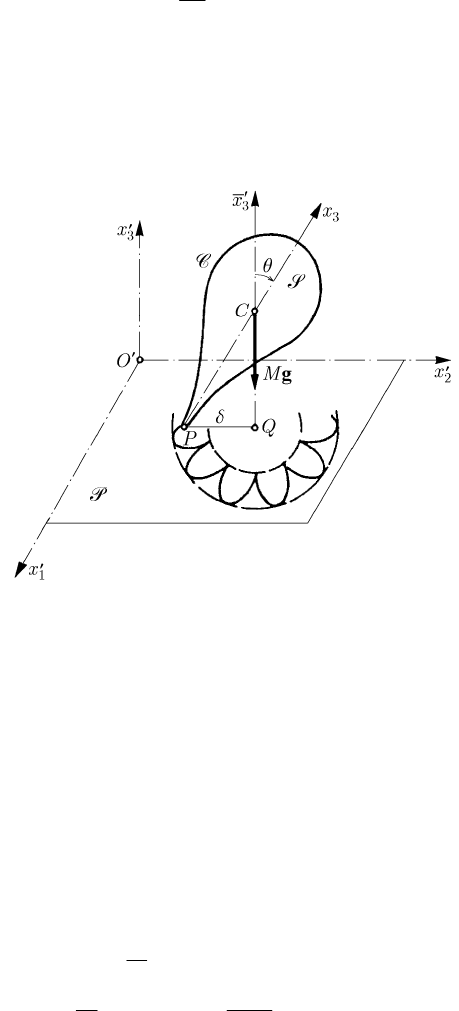
17.1.2.4 Motion of a Heavy Homogeneous Rigid Solid of Rotation Which Slides

Frictionless on a Fixed Horizontal Plane

We consider, in particular, the case of a rigid solid S for which the surface S is of

rotation with respect to the

Cx -axis, this axis being – at the same time – an axis of

symmetry for the corresponding central ellipsoid of inertia. These conditions are

fulfilled, e.g., by a heavy homogeneous rigid solid of rotation. We represent in Fig. 17.8

a meridian curve

C of a rigid solid S, the point Q being the projection of the mass

centre

C on the fixed plane P.

17 Dynamics of Systems of Rigid Solids

479

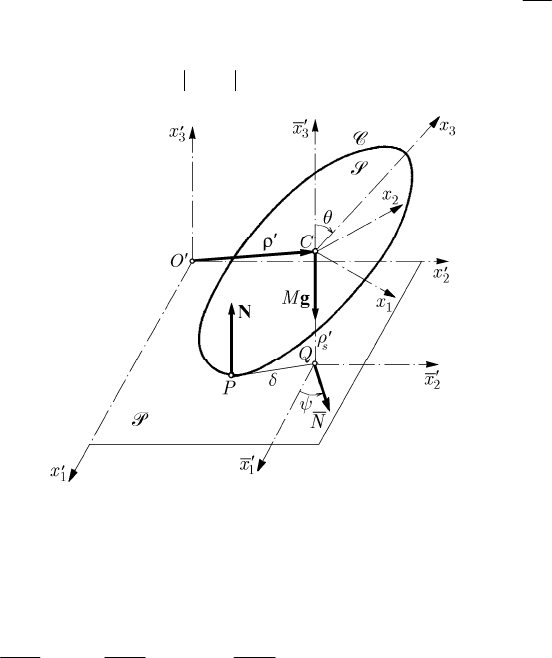
If we denote by R the angle formed by the straight line CQ with the

Cx -axis, then

we can write a relation of the form

()fSR

′

= ,

(17.1.28)

which is determined by the meridian curve

C. Choosing the

Ox -axis in the considered

meridian plane, the equation of the tangent

PQ is given by

sin cos ( )xx fRRR−=.

(17.1.29)

Because the meridian curve

C is the envelope of this tangent, the co-ordinates of the

contact point

P are obtained associating the equation

cos sin ( )xx fRRR

′

+=,

(17.1.29')

obtained by differentiation with respect to R ; this is just the equation of the straight line

which passes through

P and is parallel to the

′′

Ox -axis. The distance = PQE is, in

this case, given by

′

= ()fER

(17.1.29'')

Fig. 17.8 Motion of a heavy homogeneous rigid solid of rotation which

slides frictionless on a fixed horizontal plane

Taking into account that

M=Rg, corresponding to the own weight of the rigid

solid

S, the equations of motion (17.1.25) of the mass centre read

′

MMgN

′

=− +

(17.1.30)

MECHANICAL SYSTEMS, CLASSICAL MODELS

480

Hence, the point Q has a rectilinear and uniform motion in the plane P.

Firstly, we assume that – at the initial moment – the velocity of the mass centre is

directed towards the vertical line (along the

′′

Ox -axis) or vanishes; because the

horizontal component of this velocity is constant, it results that it will be – further –

equal to zero. Hence, the point

Q remains fixed, while the centre C oscillates along the

vertical of this point.

Applying the theorem of moment of momentum, we notice that

=M0. Because

IIJ

, the equation (17.1.26) leads to



, hence ==

constXX . As

well, the equation (17.1.26') leads to the first integral

()

′

++ =

12 33

sin sin cos cos

JIKRX K X K X R ,

(17.1.31)

where

′

is the constant component of the moment of momentum along the

Cx -axis, in the frame of reference

′

, with respect to the centre C. From (17.1.27)

we get a conservation theorem of mechanical energy in the form (in the considered

hypothesis we have

′′

d/d d/d 0ttSS )

()

22 0

12 33 3

MJ I Mgh

XX X S

′

§·

′

+++ =− +

¨¸

©¹

(17.1.32)

where

h is the energy integration constant.

Noting that the relation (17.1.28) allows to write

d/d ()tfSRR

′′



, ()=d/dffRR

′

and, using the relations (5.2.35), the first integrals (17.1.31), (17.1.32) take the form

(we associate the third relation (5.2.35))

=−

sin cosaZRBX R



[

]

22 2 2

sin 1 () ()cf bfZR RRCR

′

++ =−



cosZRKX



(17.1.33)

where we have introduced the notations

′

= ,

()

2hI

−

=>,

bgc

==>

, 0

=>;

we notice that B and C are constants which depend on the initial conditions, while

a, b

and

c depend only on the geometry and the mechanical properties of the rigid solid. We

obtain thus a system of differential equations which determine Euler’s angles

()tZZ= , ()tRR= and ()tKK= . Eliminating Z



between the first two equations,

we get the equation

[]

()

222 2 0

1()sin ()sin coscf bf aRRRCRRBXR

′

+=−−−

ªº

¬¼



(17.1.34)

17 Dynamics of Systems of Rigid Solids

481

which determines t as a function of R by a quadrature; if ()f R is a rational function of

sin R and cos R and if we take as a new variable

()

tan / 2R , then we obtain a

hyperelliptic integral. Taking into account the geometric significance of the function

()f R , specified by the relation (17.1.28), it results that the integral can take only finite

values. We notice that, for

= 0R and =RQ, the function in the second member of the

equation (17.1.34) takes negative values; for

RR, at the initial moment, the function

can take only a positive value, corresponding to a real value of



. It results

RRR<<, where

R and

R are two real zeros of the mentioned function. Thus, we

can make for the equation (17.1.34) a study analogous to that in Sects. 15.2.1.1 and

15.2.1.2. In this context, Puiseux showed that one can choose an initial angular velocity

X sufficiently great so that ()tR remain close to

at any moment t, the motion of

the rigid solid being thus stable. But Thomson showed that supplementary constraints,

instead to increase the stability of the rigid solid, could lead to a loss of the stability of

its motion (the rigid solid overturns).

We notice that the straight line

QN , normal to the meridian plane, is parallel to the

line of nodes; in this case, if we use the

′

Ox -axis, parallel to the fixed axis

′′

Ox , the

point

Q being chosen as pole, then the contact point P will be specified by the polar co-

ordinates E and

=+3/2DZ Q . The first equation (17.1.33) leads thus to the equation

()

cos

sin

aDBXR

=−

 .

(17.1.35)

Eliminating d

t between the equations (17.1.34) and (17.1.35), we find an equation with

separate variables which gives the angle Dby a quadrature as a function of the angle R;

taking into account (17.1.29''), it results a relation which links D to E. We obtain thus

the curve described by the contact point

P in the fixed plane P.

If the mass centre is not projected at a fixed point

Q on the plane P, then we observe

that this point has a rectilinear and uniform motion; we report the relative motion to a

frame of reference

′′′

123

Qx x x , observing that this frame is inertial too. Hence, the

relative motion is governed by the same differential equations as the absolute motion; in

the movable frame, the point

Q is fixed, so that the problem is reduced to that studied

above.

As an application, one can study Gervat’s gyroscope (the “equilibrist foot”)

previously considered in Sect. 16.2.1.1.

17.1.2.5 Frictionless Motion of a Heavy Gyroscope on a Fixed Horizontal Plane

The gyroscope is a rigid solid for which the ellipsoid of inertia relative to a fixed point

of it is of rotation. In our case, the fixed point is the contact point

P (at a given

moment), assuming that the gyroscope is bounded at the vicinity of this point by a

MECHANICAL SYSTEMS, CLASSICAL MODELS

482

smooth surface, e.g., spherical (even if the radius of the respective sphere is very small);

if the gyroscope is a solid of rotation, then the

PC-axis is a principal axis of inertia,

being just the symmetry axis of it. If

=CP l

, then the function ()f R is given by (Fig.

17.9)

() cosflRR= .

(17.1.36)

As well, we have

= sinlER. (17.1.36')

Fig. 17.9 Frictionless motion of a heavy gyroscope on a fixed horizontal plane

The initial conditions (at the moment

= 0t

) read

(0) (0) 0XX==,

(0)XXX==,

(0)RR= ,

(0)ZZ= ;

we associate to them

(0) 0R =



(we use the second relation (14.1.15)) and the constants

of integration are obtained in the form

cos

KIXR

′

()

22coshI MglXR=+ ,

so that

()

sin cos cos

ZR X R R=−



()

22 22 2

sin 1 sin cos cos

MMgl

ZR RR R R++ = −



(17.1.37)

17 Dynamics of Systems of Rigid Solids

483