Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

Assuming that at the contact of the two spheres intervene internal forces, hence

internal percussions, only along the direction of the centres (we neglect the friction

forces and the corresponding percussions), we can use the results in Sect.. 2.1.2

(especially the formulae (17.2.9) (for

′

and

′

), to which we associate the relations

′′ ′

= ,

′′ ′

= . In this case,

111

Vvu

′′ ′′ ′

=+,

222

Vvu

′′ ′′ ′

=+,

(17.2.12)

the angles made by the velocities

′′

V and

′′

V with the line of centres being given by

121 1

1211 222

()sin

tan

( ) cos (1 ) cos

mmV

mkmV kmV

′

′′

−++

122 2

11 1 2 1 2 2

()sin

tan

(1 ) cos ( ) cos

mmV

kmV m km V

′

′′

++−

(17.2.12')

respectively.

As well, the formulae (17.2.9) lead to

1211 222

12 1

( ) cos (1 ) cos

()cos

mkmV kmV

′′

−++

′′

11 1 2 1 2 2

12 2

(1 ) cos ( ) cos

()cos

kmV m km V

′′

++−

′′

;

(17.2.12'')

using (17.2.10), the loss of kinetic energy reads

()

1122

() 1 cos cos

TkmVV%BB

′′

=− −

111

mm m

(17.2.12''')

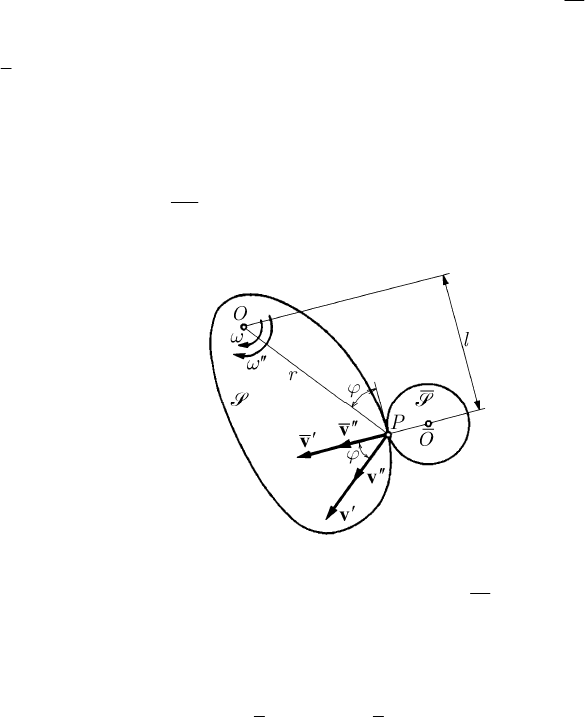
Fig. 17.17 Collision of a sphere with a fixed wall

In particular, let us consider a limit case in which one of the spheres is replaced by a

fixed wall

P, to which a sphere S strikes at the point P with a velocity

′′′

=+Vvu

which makes an angle B with the normal component

′

v (Fig. 17.17).

Neglecting the friction, the component

′

u of magnitude sinuV B

′′

= is not

modified; the component

′

of magnitude cosvV B

′′

= changes of direction after

collision, becoming

′′

v of magnitude vkv

′′ ′

= (corresponding to the relation (17.2.8),

where we make

′′′

vv0, the wall being fixed). We find thus

MECHANICAL SYSTEMS, CLASSICAL MODELS

504

222

cos

sin cos

cos

VV k kV V

′′ ′ ′ ′

=+=≤

tan tan

CB= ,

(17.2.13)

where C is the angle made by the velocity

′′

V with the normal to the plane P (see the

analogous relations (13.1.21'), (13.1.21'') too; because

1k < , it results

CB≥

. Hence,

by the collision of a sphere

S with a fixed wall P, the velocity decreases in magnitude,

while the velocity vector moves away from the normal to the wall. In case of an elastic

collision, we have

1k = ; one obtains VV

′′ ′

= and CB= , finding again Huygens’s

laws of reflection of the light photon which hits obliquely a mirror (the velocity

maintains its magnitude, while the angle of reflection is equal to the angle of incidence).

Another mathematical model has been built up by I. ğăposu in 1991; he supposed

that, besides (17.2.8), one has

′′ ′′

−

′′

−

(17.2.8')

too. He obtained thus

1211 222

()sin(1)sin

tan

( ) cos (1 ) cos

mkmV kmV

′′

++−

′′

−++

11 1 2 1 2 2

(1 ) sin ( ) sin

tan

(1 ) cos ( ) cos

kmV m km V

′′

−++

′′

++−

(17.2.14)

results identical with the classical ones for

1k = (elastic collision). The velocities after

collision are

1211 222

12 1

( ) cos (1 ) cos

()cos

mkmV kmV

′′

−++

′′

1211 222

12 1

( ) sin (1 ) sin

()sin

mkmV kmV

′′

++−

11 1 2 1 2 2

12 2

(1 ) cos ( ) cos

()cos

kmV m km V

′′

++−

′′

11 1 2 1 2 2

12 2

(1 ) sin ( ) sin

()sin

kmV m km V

′′

−++

(17.2.14')

their components being given by

11 1

cosvV C

′′ ′′

22 2

cosvV C

′′ ′′

11 1

sinuV C

′′ ′′

22 2

sinuV C

′′ ′′

. The loss of kinetic energy becomes

[]

0222

12 12 12

() (1) 2 cos( )

TkmvvvvBB

′′ ′′

Δ=− +− −

(17.2.14'')

vanishing in the elastic case (

1k = ), as in the classical model.

17 Dynamics of Systems of Rigid Solids

505

One can show that the components of the velocities normal to the line of centres

remain constant, as in the classical case, if

′′

= , that is if the velocities of the two

spheres have the same inclination on the above mentioned line.

17.2.1.5 Collision of a Sphere with a Rigid Solid in Rotation About a Fixed Axis

Let be a rigid solid

S, which is in rotation about a fixed axis, having a moment of

inertia

I with respect to it; we suppose that this solid is hit by a sphere S of mass m, in

a plane perpendicular to the axis (which contains the pole

O of the axis and the centre

O of the sphere), along the common normal at the point P (Fig. 17.18). We denote by

′

v and

′′

v the velocities of the point P before and after collision, respectively, with

respect to a fixed frame of reference with the pole at

O; the magnitudes of these

velocities, which make the angle

K with the normal at the point P, will be vrX

′′

vrX

′′ ′′

, with rOP= , where

′

ω and

′′

ω are the angular velocity vectors, before

and after collision, respectively.

Fig. 17.18 Collision of a sphere with a rigid solid in rotation about a fixed axis

In case of the mechanical system formed by

S and

appear only the external

constraint percussions at the points of the rotation axis; the moment of the percussions

with respect to this axis vanishes, so that we can write a conservative theorem of the

moment of momentum in the form

ImvlI mvlXX

′′ ′′′′

+=+

(17.2.15)

where

l is the distance from the point O to the common normal at the point P. We

notice that

cos cosvrlKX KX

′′ ′

, cos cosvrlKX KX

′′ ′′ ′′

are the components of the velocities

′

v and

′′

v , respectively, along this normal. Taking

into account the study made in Sect. 17.2.1.2, we introduce the coefficient of restitution

MECHANICAL SYSTEMS, CLASSICAL MODELS

506

(to fix the ideas, we assume that cosvv K

′′

; otherwise, both the signs of the

denominator and of the numerator change)

cos

vv v l

′′ ′′

−

′′ ′ ′

−−

(17.2.16)

The relations (17.2.15), (17.2.16) lead to

()

vv k v l

Iml

′′ ′ ′ ′

=−+ −

()

kvl

Iml

XX X

′′ ′ ′ ′

=++ −

(17.2.17)

As well, the loss of the kinetic energy will be given by

()

Tkvl

Iml

′′

=− −

(17.2.18)

The elastic collision (

1k =

) takes place without loss of kinetic energy; in exchange,

the natural collision (

01k<<

) takes place with loss of kinetic energy, which is

maximal in case of a plastic collision (

0k =

), being given by

()

Tvl

Iml

′′

=−

(17.2.18')

17.2.1.6 Collision of Two Arbitrary Rigid Solids

Let us consider now two rigid solids

S and

S of masses

M and

M and mass

centres

C and

C , respectively, which are in collision at the moment

t , the point of

impact being

P (Fig. 17.19). We denote by

′

and

′

and

′′

and

′′

, the

velocities of the mass centres before and after collision, respectively, with respect to a

given fixed frame of reference

′

; in this case, the theorem of motion of the mass

centre (the formula (13.1.24'')), applied to each rigid solid, gives

Fig. 17.19 Collision of two arbitrary rigid solids

()

′′ ′

−=−vv P,

()

′′ ′

−=vv P,

(17.2.19)

17 Dynamics of Systems of Rigid Solids

507

where P is the percussion, applied at the point P, by which the rigid solid

S acts upon

the rigid solid

S . As well, if

′

and

′′

, are the angular momenta of

the two solids with respect to the corresponding mass centres, in the movable frames

R and

R , rigidly linked to the respective solids, with the poles at these centres,

before and after collision, respectively, then we can write the theorem of moment of

momentum (the formula (13.1.25)) with respect to each centre of mass, in the

mentioned frames, in the form

′′ ′

−=−×

KK rP,

′′ ′

−=×

KKrP,

(17.2.19')

where

CP=

JJJG

r ,

CP=

JJJG

r ; we obtain thus four vector equations (17.1.25), (17.1.25')

(12 scalar equations) for the five vector unknowns

′′

v ,

′′

v ,

′′

K ,

′′

K and P (15

scalar unknowns).

We assume that at the contact point

P do not appear constraint percussions, the

solids

S and

S being perfectly smooth, and we can write

P=Pn, 0P > , (17.2.20)

where

n is the unit vector of the common normal at the point P, with the sense from the

solid

S to the solid

S ; thus, the number of the scalar unknowns is reduced to 13.

Otherwise, it is necessary to introduce supplementary hypotheses concerning the

phenomenon of friction (we can introduce, e.g., a Coulombian sliding friction).

The velocities of the points

and

of the solids

S and

S , respectively, which

coincide with the point

P at the theoretic moment of impact, are expressed, with respect

to the fixed frame of reference

′

, in the form

=+×vv rω

(17.2.21)

where

ω and

ω are the angular velocities of the frames

R and

R , respectively,

with respect to the frame

′

. The relative velocity of the point

P with respect to the

point

P will, obviously, be

()

−⋅vvn

, hence a velocity of compression,

corresponding to the respective phase (the interval of time

[

)

,tt

′

); the respective

velocity vanishes at the end of the phase and we may write

()

−⋅=vvn, so

that the common velocity at the theoretic moment

t will be

00 0

=⋅=⋅vvnvn

(17.2.22)

As well, the equations (17.2.19), (17.2.19') read

()

′

−=−vv n,

()

′

−=vv n,

(17.2.23)

()

′

−=−×KK r n,

()

′

−=×KK r n.

(17.2.23')

MECHANICAL SYSTEMS, CLASSICAL MODELS

508

These four vector equations, together with the scalar equation (17.2.22), where we take

into account (17.2.21), allow to determine the velocities

v ,

v and the angular

momenta

K ,

K , at the end of the phase of compression; in these relations, we take

into account that the angular momenta

′

K , and

′

K are expressed as functions of the

rotation angular velocity vectors

′

and

′

, respectively, so that the number of the

unknown vectors is not great.

The velocity

v of the point P at the end of the compression phase (the moment

t )

is given by (13.2.22), the corresponding percussion being

()()

11 22

CC CC

PM M

′′

=−⋅=−⋅vvn vvn.

(17.2.24)

By introducing the coefficient of restitution

k, the percussion corresponding to the

restitution phase will be given by

k=PP, so that

()

cr c

k=+=+PP P P or

()

1 kP=+

Pn, (17.2.25)

the percussion

P being entirely determined. Replacing in (17.2.19), (17.2.19'), the

problem can be completely solved.

One can show that, in case of an elastic collision (

1k =

), the kinetic energy is

conserved (

() 0TΔ=

17.2.1.7 Theorems of Extremum

Let be a discrete system

S of particles

P , of masses

m , driven by the velocities

′

and

′′

v before and after collision, respectively, and acted upon by the given and

constraint percussions

P and

P , 1,2,...,ip= , respectively. These particles can be

rigid solids too, modelled as particles, for which we assume that the rotation angular

velocities have not jumps in the interval of percussion. We can write the theorem of

momentum in the form

()

ii i i

′′ ′

−=+vv PP, 1,2,...,ip= ,

(17.2.26)

for each particle; effecting a scalar product of these equations by the arbitrary vectors

w ,

1,2,...,ip=

, and summing, we get

()

ii i i i i

′′ ′

−⋅= + ⋅

¦¦

vvw PP w.

(17.2.26')

We notice that this relation is of the form of the principle of virtual velocities (the

formula (13.1.57')).

The mechanical system

S can be subjected to constraints which are maintained

during the application of the percussions, can appear suddenly or can disappear in this

interval of time (as it has been shown in Sect. 17.2.1.1). If

w are velocities which

satisfy the constraint relations, then the relation

17 Dynamics of Systems of Rigid Solids

509

⋅=

(17.2.27)

corresponding to the relation which defines the ideal constraints, takes place.

If we take into account (17.2.27) and assume that

′′

⋅=

(17.2.28)

for

′′

wv, then it results

()

ii i i

′′ ′ ′′

−⋅=

vvv .

We can write

()

() ()

111

ppp

ii i i i i i i i i

iii

TT mv v m m

===

′ ′′ ′ ′′ ′′ ′ ′′ ′ ′′

−= − = − − − ⋅

¦¦¦

vv vvv.

Introducing the kinetic energy of the lost velocities, we get

()

0TT% =>

(17.2.28')

and we can state

Theorem 17.2.1 (Carnot, I) If upon a discrete mechanical system S does not act any

given percussive force, then the sudden apparition of a constraint leads to a loss of

kinetic energy.

This theorem can be put in connection with the Theorem 13.1.5.

If we assume that

′

wv and that

′

⋅=

Pv ,

(17.2.29)

then it results

()

ii i i

′′ ′ ′

−⋅=

vvv ,

where we took into account (17.2.27). We can write

()

() ()

111

ppp

ii i i i i i i i i

iii

TT mv v m m

===

′′ ′ ′′ ′ ′′ ′ ′′ ′ ′

−= − = − + − ⋅

¦¦¦

vv vvv,

so that

MECHANICAL SYSTEMS, CLASSICAL MODELS

510

()

0TT% =>,

(17.2.29')

and we may state

Theorem 17.2.2 (Carnot, II) An internal “explosion” in a non-deformable discrete

mechanical system

S leads to a “tearing” of its rigidity, with an increase of the kinetic

energy.

As a matter of fact, by “explosion” we intend the action of an internal percussive

force, which leads to an increase of the distance between the particles, the mechanical

system becoming deformable (the distances between two arbitrary particles do no more

remain constant in time). This result can be put in connection with the Theorem 13.1.6.

Let be a discrete mechanical system

S at rest with an inertial frame of reference; we

assume that one applies percussive forces upon some of the particles

P , so that these

particles have prescribed velocities

′′

v . Let us consider, as well, a possible motion,

which satisfies the constraints of the system, the considered particles having the

velocities

v . Let us denote

iii

′′

=−

wvv and let us suppose that

′′

vv; in this

case

⋅=

Pw ,

(17.2.30)

because

=w0 for the particles mentioned above, while

=P0 for the other

particles. Observing that the relation (17.2.27) takes, as well, place and assuming that

′

v0, the relation (17.2.26') reads

()

ii i i

′′ ′′

⋅−=

vvv

and we have

()

() ()

111

ppp

ii i iii ii ii

iii

TT mv v m m

===

′′ ′′ ′′ ′′ ′′ ′

−= − = − − ⋅ −

¦¦¦

vv vvv,

so that

()

0TTΔ=>,

()

TTT

′′

Δ=−,

()

ii i

′′

=−

vv;

(17.2.30')

we can thus state

Theorem 17.2.3 (Kelvin) If a discrete mechanical system S, at rest with respect to an

inertial frame of reference, at the initial moment, is put in motion by percussive forces

which act upon some of its particles, so that to these particles are impressed prescribed

velocities, then the corresponding kinetic energy is smaller than the kinetic energy of

any possible motion which satisfies the constraints of the system, the considered

particles having the same prescribed velocities.

17 Dynamics of Systems of Rigid Solids

511

Let

′

v an

′′

v be the velocities of the particles of a mechanical system

, with the

general significance previously given (the velocities before and after the application of

the percussive forces, respectively, assuming that the system is subjected to certain

constraints); in case of the existence of supplementary constraints, consistent with the

motion of the system

S before the collision, the application of the same percussive

forces leads to the velocities

v after the percussion interval. For

=wv takes place

a relation of the form (17.2.27) in both situations; indeed, in the second case intervene

only supplementary constraint forces. The relation (17.2.26') leads to

()

ii i i i i

′′ ′

−⋅= ⋅

¦¦

vvv Pv,

()

ii i i i i

′

−⋅= ⋅

¦¦

vvv Pv;

subtracting the two relations one from the other, we obtain

()

ii i i

′′

−⋅=

vvv .

(17.2.31)

We can write

()

() ()

111

ppp

ii i i i i i i i i

iii

TT mv v m m

===

′′ ′′ ′′ ′′

−= − = − + − ⋅

¦¦¦

vv vvv,

so that

()

0TTΔ=>,

() ()

TTΔ=−Δ,

(17.2.31')

with the notations in (17.2.30'); we state

Theorem 17.2.4 (Bertrand) The kinetic energy corresponding to the application of

some percussive forces upon a discrete mechanical system

S, in motion with respect to

an inertial frame of reference, is greater than the kinetic energy corresponding to the

application of the same percussive forces upon the same initial motion, assuming that

supplementary constraints, consistent with the mentioned motion, have been

introduced.

17.2.2 Motion of a Rigid Solid Subjected to the Action of a Percussive

Force

In what follows we consider the motion of a free or constraint rigid solid (with a fixed

axis or with a fixed point) subjected to the action of a percussive force or suddenly

fixed; the results thus obtained will be applied to the ballistic pendulum.

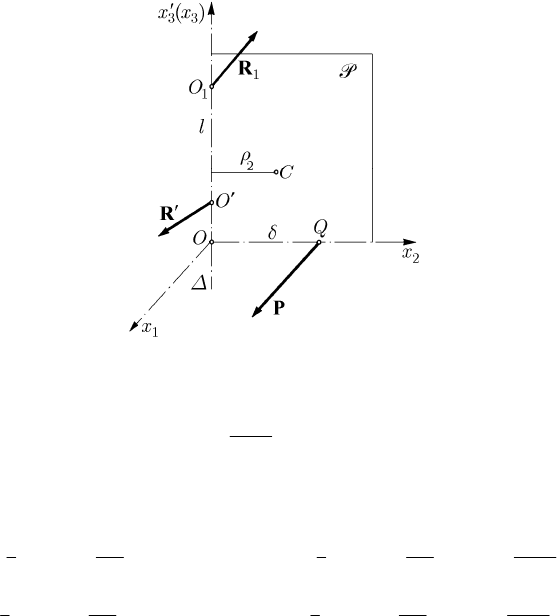
17.2.2.1 Motion of a Rigid Solid with a Fixed Axis Subjected to the Action

of a Percussive Force. Centre of Percussion

Let us consider a rigid solid

S with a fixed axis % (specified by the fixed points O

′

and

O , situated at a distance l one of the other). We choose a fixed frame of reference

MECHANICAL SYSTEMS, CLASSICAL MODELS

512

′

with the

′′

-axis along

′

and a movable frame R with the pole O on the

fixed axis (in general,

O distinct from O

′

) and with the

Ox -axis along

OO too (Fig.

17.20). We obtain thus the jump relations (17.2.5), (17.2.5'), corresponding to the

theorems of momentum and moment of momentum. We find thus the jump of the

angular velocity

Fig. 17.20 Motion of a rigid solid with a fixed axis subjected

to the action of a percussive force

()

XΔ= ,

(17.2.32)

as well as the components of the constraint percussions

RMM

§·

=− −

¨¸

©¹

23 3

11 2

33 33

RR M M M

lI I

§·

′

=− + − −

¨¸

©¹

RM M

§·

=−

¨¸

©¹

31 3

22 1

33 33

RR M M M

lI I

§·

′

=− − − +

¨¸

©¹

(17.2.32')

The other two components remain non-determinate, because one can know only their

sum (

313 3

RR R

′

+=); the rigid solid is statically indeterminate from this point of

view.

Let be the case in which upon the rigid solid

S acts only one percussive force,

which leads to the percussion

P (

RP= , 1, 2, 3i = ). The problem is put to find the

conditions in which the constraint percussions at

O and

O vanish (jerks do not appear

in the axis of rotation); we must have

′

==, 1, 2, 3i = . In the first case, it

results

0P = , so that the percussion must be normal to the axis of rotation. We

choose the

Ox -axis parallel to P, so that to have

0P = , hence

PP= . To simplify

17 Dynamics of Systems of Rigid Solids

513