Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

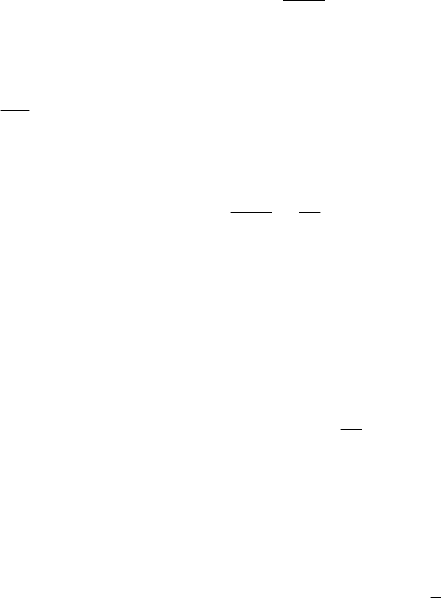
the calculation, we assume that the percussion P is applied at the point Q on the

-axis; it results

MM==

too. From (17.2.32') we find the conditions

31 23

0II==,

0S = . Hence, the percussion P must be normal to the

Ox x -plane,

which contains the mass centre

C. As well, the axis of rotation must be a principal axis

of inertia at the point

O at which the plane which contains the percussion and is normal

to the axis is pierced by it.

We notice that

()

Δ=− ,

(17.2.33)

corresponding a loss or an increase of angular velocity, as

P and

S have the same

sign or are of opposite signs. Because

MPE=− (in the hypothesis

0P > ), where

OQE = , Q being on the half-straight line

Ox (Fig. 17.20), the relations (17.2.32),

(17.2.33) lead to (

is the gyration radius corresponding to the axis of rotation)

33 3

==,

(17.2.34)

the position of the point

Q, called centre of percussion, being thus specified. Using the

Huygens-Steiner theorem, the formula (3.1.113') allows to write

22 2

iiS=+, where

i is the gyration radius corresponding to an axis which passes through the centre of

mass

C and is parallel to the rotation axis; in this case,

lES S=+>,

= ,

(17.2.34')

the centre of percussion being farther from the axis of rotation than the centre of mass.

In fact,

E is the length of the mathematical pendulum synchronous with the physical

pendulum, formed by the rigid solid which is in rotation about the fixed axis

′

. All

the results obtained in Sect. 14.2.1.2 for the physical pendulum can be adapted to the

problem considered above. For instance, to a fixed axis

Qx (parallel to the

Ox -axis),

which is the principal axis of inertia for the rigid solid

S, corresponds the percussion

centre

O. We can thus state

Theorem 17.2.5 If the fixed axis % of a rigid solid S, which is in rotation, is a

principal axis of inertia for a point

O of it, then any percussion normal to the meridian

plane

P of the mass centre C (plane determined by the axis % and the centre C) at a

point of it, situated on a normal at

O to the axis %, at the distance E of it and on the

same part with the centre

C, does not give constraint percussions on the axis %.

MECHANICAL SYSTEMS, CLASSICAL MODELS

514

Hence, to any straight line %, principal axis of inertia at a point O of a rigid solid,

corresponds a centre of percussion

Q, so that on the axis %, as axis of rotation, do not

arise any constraint percussion. In particular, in case of a plate, to any straight line in

the plane of the plate corresponds a centre of percussion.

One can put also the inverse problem: The centre of percussion

Q being given, it is

asked to determine the position of the axis

% (of rotation) which is not acted on by the

phenomenon of collision. For instance, a blacksmith which strikes the anvil with the

hammer (at the point

Q) knows, instinctively, how to take the hammer so that not to

feel at the palm (at the point

Q) a too great shock (the point O is the point at which the

axis

% pierces the plane in which the hammer is rotating).

17.2.2.2 The Ballistic Pendulum

The ballistic pendulum is a device intended to measure the velocity of the projectiles,

formed by a metallic cylinder (e.g., of pig iron) filled up with a soft and viscous

material (e.g., earth); it is fixed at a point

′

and oscillates about a horizontal axis

′′

, its position being specified by an angle R made with the descendent vertical

′′

. The

Ox x

′′′

-plane is a plane of symmetry of the mechanical system S, passing

through the mass centre

C, situated at the distance

′

from the pole O

′

. At the initial

moment, the mechanical system

S is at rest with respect to the frame of reference

′

A projectile of mass

m, launched horizontally, at the distance

lES

′

from the

fixed point

′

, in the plane of symmetry, with the velocity v, strikes the pendulum and

remains fixed at the point

′

(specified by the angle B made by

′′

with the

′′

-axis and by OQ l

′′ ′

= ), on the horizontal of the point Q of the

′′

-axis (Fig.

17.21). The problem is put to determine the velocity

v if the angle

max

RR= ,

corresponding to the oscillations of the physical pendulum, is known.

The percussions between the projectile and the pendulum are internal and the

moment at

′

of the percussions of the

′′

-axis vanishes, so that we can apply a

conservation theorem of moment of momentum of the mechanical system

S formed by

the pendulum and the projectile. The moment of momentum before the interval of

collision is

mvE, after collision being equal to

()

Iml X

′

, where I is the moment of

inertia with respect to the

′′

-axis, while

X is the angular velocity of the

mechanical system

S ; equating these angular momenta, we get

Iml

′

(17.2.35)

To the mechanical system

S one can apply the theorem of moment of momentum

with respect to the

′′

-axis in the form

17 Dynamics of Systems of Rigid Solids

515

()

[]

sin sin( )

Iml Mg mgl

XSR RB

′′′

+=− − +

M being the mass of the pendulum; multiplying by XR=



and integrating, there results

the relation

()()

[

]

{}

222

2 (1 cos ) cos cos( ) 0Iml gM mlXX S R B RB

′′′

+−+ −+−+=

(17.2.36)

corresponding to the theorem of kinetic energy, where, at the initial moment of this

motion (which coincides to the end of the interval of percussion), we imposed the

conditions

0R =

and

XX= .

Fig. 17.21 The ballistic pendulum

Making

RR= and

0X =

, we obtain

000

sin sin sin

222

Mml

Iml

RRR

XS B

ª§·º

′′

=++

¨¸

«»

′

¬©¹¼

(17.2.37)

wherefrom

()

000

sin sin sin

222

gI ml

vMml

RRR

′

ª§·º

′′

=++

¨¸

«»

¬©¹¼

(17.2.38)

We notice that

cosl BE

′

If the projectile stops at the point

Q on the

′′

-axis, then we have 0B = , so that

2sin

′

(17.2.37')

MECHANICAL SYSTEMS, CLASSICAL MODELS

516

the velocity of the projectile being

()

() sin

vgMmIm

SE E

′

=++

(17.2.38')

The angle

R is measured experimentally on an indicator dial.

We observe that, in the given conditions, the

′′

-axis is a principal axis of inertia.

The pendulum is not acted upon by percussions on its axis of suspension (to have an as

small as possible wear of the device in running) if the projectile remains fixed at the

centre of percussion, hence at the point

Q, so that

/iIMSE

′

. We find thus

()

sin

vMm

′

(17.2.39)

17.2.2.3 Motion of a Rigid Solid with a Fixed Point Subjected to the Action

of a Percussive Force

Let be a rigid solid with a fixed point

′

≡ , subjected to the action of a percussive

force, which leads to the percussion

P applied at the point Q; at the fixed point appears

a constraint percussion

P . We denote by

′

and

′′

the rotation angular velocities

before and after the interval of collision, respectively. The theorem of moment of

momentum with respect to the frame of reference

R reads

()

Δ=I ω M ,

()

′′ ′

Δ=−

ω ω ω

(17.2.40)

the moment of the percussion

P vanishing, while

M is the moment of the percussion

P (eventually, the resultant moment of a certain number of given external percussions).

Projecting on the principal axes of inertia corresponding to the point

O, it results

()

XΔ= ,

()

XΔ= ,

()

XΔ= ,

(17.2.40')

obtaining thus the jumps of the angular velocity. The equation of motion of the mass

centre (17.2.4) allows to express the components of the constraint percussion in the

form

132

PPM

§·

=− + −

¨¸

©¹

213

PPM

§·

=− + −

¨¸

©¹

321

PPM

§·

=− + −

¨¸

©¹

(17.2.41)

17 Dynamics of Systems of Rigid Solids

517

Introducing the ellipsoid of inertia

E, given by the equation (15.1.63), we can

consider the plane which passes through the fixed point

O and the moment

M , of

equation

123

OO O

Mx Mx Mx++=,

which can be written in the form

() ()

1 112 223303

() 0IxIxIxXXXΔ+Δ+Δ=

(17.2.42)

too. The diameter conjugate to this plane, with respect to the ellipsoid

E, will be of

equations

()()()

123

000

xxx

XXX

ΔΔΔ

(17.2.42')

representing just the support of the vector

()Δωω .

Hence, if we draw a plane tangent to the ellipsoid of inertia

E, normal to the

direction of the resultant moment

M of the given percussions (taken with respect to

the fixed point

O), the jump of the angular velocity vector

()Δωω will be situated along

the position vector of the tangent point (conjugate diameter of the considered plane). If,

before the interval of collision, the rigid solid

S is at rest (

′

0ω ), then, after the

action of the percussive forces, this solid begins to rotate about the support of the

position vector of that point of the ellipsoid

E at which the tangent plane is normal to

the resultant moment of the percussions, with respect to the fixed point

O. The

connection between the considered mechanical phenomenon and the geometric aspect

given by Poinsot to the Eulerian case of motion of a rigid solid with a fixed point is thus

put in evidence.

17.2.2.4 Motion of a Free Rigid Solid Subjected to the Action of a Percussive Force

Let us consider a free rigid solid

S, subjected to the action of a percussive force, which

leads to the percussion

P applied at the point Q. We denote by

′

v ,

′′

v and

′

′′

the velocities of the mass centre

C and the rotation angular velocities of the rigid solid

about this point, with respect to an inertial frame of reference

′

, before and after the

interval of percussion, respectively. The equations (17.2.1), (17.2.3) read

()

M Δ=v R

(17.2.43)

()

Δ=I ω M ;

(17.2.43')

we can thus calculate easily the jumps

()

CCC

′′ ′

Δ=−

vvv

and

()

′′ ′

Δ=−

ω ω ω

. We

get

()

Δ=

v R ,

(17.2.44)

MECHANICAL SYSTEMS, CLASSICAL MODELS

518

as well as (we use the central principal axes of inertia of the rigid solid

S )

()

XΔ=

()

XΔ=

()

XΔ=

(17.2.44')

Obviously, these results can be applied in case of an arbitrary number of external

percussions too.

17.2.2.5 Motion of a Rigid Solid Subjected Suddenly to a Fixation

One can study an inverse problem too: a rigid solid

S has an arbitrary motion; if, at a

given moment, one of its points is suddenly fixed, then the velocities of all points will

have jumps, intervening also the effect of unknown constraint forces. In this case too,

one must determine the velocities after fixing.

For instance, let us consider a rigid solid with a fixed point

′

and let us assume

that, at a given moment

t , a second point

O is fixed, so that the rigid solid S moves

now as a solid with a fixed axis. If

versOO

′

JJJJG

u , then we can write

()

′

Δ⋅=Ku,

()

OOO

′′′

′′ ′

Δ=−

KKK (putting in evidence the moment of

momentum after and before the collision, respectively), because the moment of the

constraint percussion which arises at

O vanishes in projection on the fixed axis

′

After the fixation of the point

, we will have

I X

′

′′ ′′

⋅=

Ku , where I is the moment

of inertia with respect to the new axis of rotation, while

′′

is the corresponding

angular velocity. We can write

′

′′

KIω , where

′

ω is the angular velocity before

fixation, with respect to an inertial frame of reference

′

with the pole at OO

′

≡ .

Thus, takes place the relation

()

I X

′′′

⋅=

Iuω ,

(17.2.45)

which determines the angular velocity

′′

(the initial velocity for the motion after

fixation); in a developed form, after the principal axes of inertia at

O, we have

111 222 333

Iu Iu I u IXXXX

′′′′′

++=

(17.2.45')

The motion is studied further using the results obtained in case of the rigid solid with a

fixed axis.

17.3 Applications in Dynamics of Engines

After some general results with a theoretical character concerning the dynamics of

engines, we deal with some applications concerning their running; we mention,

especially, the equilibration of the movable masses and the regulation of the working of

engines.

17 Dynamics of Systems of Rigid Solids

519

17.3.1 General Results

We call engine (machine) a set of mechanisms (a mechanical system

S, formed by n

rigid solids, eventually deformable,

, 1,2,...,jn= ), which perform prescribed

motions, with the goal to realize a useful work or to transform a mechanical energy. A

machine is formed, in general, by three parts: the driving mechanism, the transmission

gear and the mechanism of execution.

In the following, we present firstly some elements of kineto-statics, putting in

evidence the forces of inertia which act upon the engines. As well, we introduce some

mechanical quantities (reduced mechanical quantities), which can characterize the

motion of a machine in its totality (mass, moment of inertia, force, power).

17.3.1.1 Forces of Inertia which Act Upon the Machines. Elements

of Kineto-Statics

Upon a machine act: (i) given forces (which are external and known), as driving forces,

forces of technological resistance, forces of weight, forces of inertia, resistance of the

medium etc. and (ii) unknown forces, e.g., constraint forces in kinematic couples, forces

of friction, forces of balancing etc. They can depend on position, velocity and time or

only on some of these factors.

At the small devices, with reduced velocities, the forces of inertia can be – in general–

neglected, unlike the big devices (with great velocities), to which they can have

values of the same order of magnitude as that of the external forces. Let be

{}

{

}

′′

τ=FRM and

{

}

{

}

iii

′′

τ=FRM the torsors of the given and inertia

forces, respectively, with respect to a fixed pole

′

, for an element of the device (of

the mechanical system

S ). Corresponding to d’Alembert’s theorem 11.1.26, we can

write

{

}

{}

′′

τ+τ=FF0,

+=RR0,

′′

+=MM0.

(17.3.1)

Taking into account the universal theorems of mechanics, it results

′

=−

′

=−

(17.3.2)

the differentiation taking place with respect to the inertial frame of reference

′

Choosing a non-inertial frame

R having the pole at the mass centre C, the torsor of the

forces of inertia at this point is given by (corresponding to the equations (14.1.47),

(14.1.48))

′

=−

(17.3.3)

()

CC C

=− − ×



MI Iω ω ω ,

(17.3.4)

MECHANICAL SYSTEMS, CLASSICAL MODELS

520

where M is the mass of the considered element,

′

v is the velocity of the centre of

mass,

ω is the rotation angular velocity vector, while

I is the central tensor of inertia.

Denoting by

′

the position vector of the mass centre, we can write

′

=−

1, 2, 3j =

(17.3.3')

Analogously, we can write

()

[]

11 3 2 23

MIIIXXX=− + −



()

[]

22 1 3 31

MIIIXXX=− + −



()

[]

33 2 1 12

MIIIXXX=− + −



(17.3.4')

where we used the central principal axes of inertia,

123

III≥≥ being the

corresponding principal moments of inertia.

In case of a motion of translation (

= 0ω ), it results

′

=−

=M0,

(17.3.5)

the system of inertia forces of the element being thus reduced to a unique force of

inertia applied at the centre of mass and equal to the product, with a changed sign, of

the mass of the element by the acceleration of its centre of mass. We notice thus that, by

the starting of the motor, when the element has an accelerated motion, the force of

inertia is a resistant force; instead, at the stopping of the motor, the force of inertia

becomes a driving force. In particular, if

d/d

′′

=av , then the element has a

rectilinear and uniform motion and is no more acted upon by a force of inertia.

In the hypothesis of a motion of rotation about a central principal axis of inertia (let

0XX==,

XX= ), we get

=R0,

33 3

IIX=− =−



Miω .

(17.3.6)

Hence, in case of the rotation of an element of the engine about one of these axes, the

system of forces of inertia is reduced to a couple, the moment of which is situated along

the axis of rotation, having its sense opposite to that of the angular velocity vector. As

above, there appear the notion of resistant couple and the notion of driving couple (due

to which the great and heavy runners (

I is greater) are rotating for a long time after

the ceasing of the action of the couple which produced the motion). If, in particular,

constX = , then the element has a motion of uniform rotation, non-being acted by any

force of inertia.

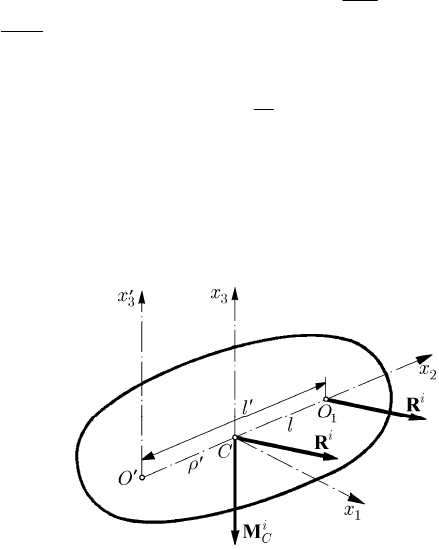
Let be now the case of rotation of the considered element about a principal axis of

inertia (the

′′

-axis), parallel to a central one (the

Cx -axis); hence,

0XX==,

XX= and we have

17 Dynamics of Systems of Rigid Solids

521

′

=−Ra,

I=−



M ω .

(17.3.7)

Observing that

′′′

⊥a (the centre C has a motion of rotation in a plane normal to

′′

), hence

′

⊥



a ω , it results that the scalar of the torsor of the forces of inertia

vanishes (

⋅=RM

, so that this system of forces is reduced to a resultant applied

at the point

O , on the straight line OC

′

(obviously, we choose the point

conventionally, the force

R , applied at

O , sliding along its support) (Fig. 17.22). We

choose the

Cx -axis along OC

′

and the

Cx -axis so that the frames

′

and R be

right-handed ones. Projecting on the axes of the frame

R, we obtain (we take into

account the intrinsic components of the acceleration

′

a , that is

a SX

′′

=−



a SX

′′

=−

)

RMSX

′



RMSX

′

=−

0R = ,

MM==,

MIX=−



(17.3.7')

The position of the point

O will be specified by

113

lCO M R IMS

′

==− =

so that (

lOO

′′

= )

llS

′′

′

(17.3.8)

where

i is the central radius of gyration with respect to the

Cx -axis. We notice that

the point

′

is a centre of suspension, while the point

O is a centre of oscillation of

the element, considered as a physical pendulum,

′

being the length of the

mathematical pendulum synchronous with this one.

Fig. 17.22 Rotation of an element of the engine about a principal axis of inertia

In case of a plane-parallel motion we have

0XX==

XX= (we choose the

Cx x

-plane as fixed plane), hence the torsor of the forces of inertia will be of the form

(17.3.7) too. The scalar of the torsor will be also equal to zero, so that the system of the

MECHANICAL SYSTEMS, CLASSICAL MODELS

522

forces of inertia is reduced to a resultant along the central axis, contained in the fixed

plane of equation (see the equation (2.2.31''))

iii

21 12

MxRxR+−=;

(17.3.9)

we associate the relations

RMa

′

=−

RMa

′

=−

MIX=−



(17.3.9')

The distribution of the accelerations is, in general, unknown; it can be obtained starting

from the accelerations of two points of the element and using the polygon of

accelerations and the method of the pole of accelerations (see Chap. 5, Sect.. 2.3.4 too).

The problem becomes complicated in case of elements of arbitrary shape, having a

complex motion; in this case, one can use the method of concentration of masses,

replacing the mass

M of the considered element by a system of masses

concentrated at the concentration points

P ,

1,2,...,in=

, chosen so that the action of

the new system of masses upon the other elements of the system be equivalent with the

action of the mass of this element. In this case, the sum of the torsors of the forces of

inertia corresponding to the concentrated masses, with respect to the mass centre, must

be equal to the torsor of the forces of inertia of the studied element, with respect to the

same centre. It is necessary that: (i) the sum of the concentrated masses be equal to the

mass of the element; (ii) the mass centre of the system of concentrated masses does

coincide with the mass centre of the element, their accelerations being equal. This

corresponds to a static repartition of the mass of the element. To obtain a dynamic

repartition of this mass, it is also necessary that: (iii) the sum of the kinetic energies of

the concentrated masses be equal to the kinetic energy of the element (hence, the sum of

the moments of inertia of the concentrated masses with respect to the mass centre be

equal to the moment of inertia of the element with respect to the same centre). It is

convenient that the points

P be on the axes of the articulations, being possible that one

of them does coincide with the centre of mass

C of the element. Practically, the mass

of an element is replaced by two or three concentrated masses.

Once the forces of inertia determined, the constraint forces of the kinematic couples

can be calculated by usual methods from the static study of the mechanical system

(analytical methods, grapho-analytical methods and graphic methods).

17.3.1.2 Kinetic Energy of an Engine

The kinetic energy of an engine can be calculated starting from the kinetic energy of

each element

S ; the quantities which intervene will be calculated with respect to a

fixed frame of reference

′

. In case of an element individualized by the index j, in

motion of translation, we have

TMv

′′

= ,

(17.3.10)

17 Dynamics of Systems of Rigid Solids

523