Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

This result can be used, e.g., in the study of the immobile flight of the aircraft with

vertical take-off (we make

==va0 and = 0ω ).

Introducing the relative acceleration

/ t∂∂ρ of the mass centre C of the

mechanical system, as well as the Coriolis acceleration

× wω

, we obtain the

equation of motion of this centre with respect to the inertial frame of reference

′

the form

hh ll

MQQ MM

∂

=+ − − − ×+ + ×

∂

∑∑

Rw w H w

ωω

(16.3.48)

where

u is the absolute velocity of the centre C.

We decompose the resultant of the given forces in the form

=+RR R, where

R is the resultant of the forces of static pressure, while

R is the resultant of the

other given external forces. If

p is the static pressure on the surface S of the outer-

covering of the aircraft, then we will have

hh ll

Sp A A

⎛⎞

⎜⎟

⎝⎠

∑∑

∫∫

pnn,

where

A and

A are the areas of the sections of entrance and exit, respectively,

supposed to be plane, while

n and

n are the unit vectors of the corresponding

external normals. Denoting by

p and

p the mean pressure on the same surfaces of

entrance and exit, respectively, it results

hhh

eeee

SpA=−

∫∫

pn, d

lll

iiii

SpA=−

∫∫

pn.

Finally, we can write

() ()

hhh lll

peee

iii

ppA ppA

=− +−

∑∑

Rnn

(16.3.49)

The equation of motion of the mass centre (16.3.48) becomes thus

2( )

MMM

∂

=+−+ −×−

∂

RT H w

(16.3.50)

where the force of traction developed in the aeroreactive system of propulsion has been

introduced in the form

() ()

hh h hh ll l l

ee e ee

ii i ii

QppA QppA

=+−−+−

⎡

⎤⎡ ⎤

⎣

⎦⎣ ⎦

∑∑

Tw n w n.

(16.3.50')

16 Other Considerations on the Dynamics of the Rigid Solid

453

We mention that the supplementary terms (excepting the forces

and T) which

appear in the equation (16.3.50) can present a particular interest, e.g., in the study of the

motion and of the stability of the vehicles with a vertical take-off-landing. If, in

particular, the vehicle is fitted out with rocket motors, then one takes

Q = , 0

p = ,

1,2,...,

hn= , in the expression of the force of traction.

Applying the theorem of momentum for the current of fluid which enters through the

section

S , in case of a motion of rectilinear and uniform translation, the flow is

stationary and we can write

()()

hh hhh

ee c eee

QppA++− =wv n0, so that the function

of traction becomes

()

ll l ll

ii i ii

QQppA

=− − − −

⎡

⎤

⎣

⎦

∑

Tv w n

(16.3.50'')

16.3.3.3 The Motion About the Centre of Mass

We notice that the position of a particle of solid, liquid, air or

gas is specified by

′′ ′

=+=+

rr r r

, where

is the position vector in a Koenig

frame of reference, its absolute velocity being written in the form

=+uvw, where

the velocity of transportation is given by

()

′′

=+×=+×+

vv rv rωω

=+×vrω . The moment of momentum with respect to the pole O

′

, in the frame

′

R , reads

′

′′′

=× + +KHKKρ

, d

Vμ=×

∫∫∫

Krw, ()d

Vμ=××

∫∫∫

Krrω ,

(16.3.51)

where

and

K are the momenta of momentum with respect to the mass centre C,

in the frame

R and in the frame

()C

of Koenig, respectively, and where we have

taken into account that the static moment of the mechanical system

S with respect to

the mass centre vanishes. Differentiating with respect to time, in the fixed frame of

reference, and taking into account that

CCC

=+uvw

, /

t=∂ ∂w

and

′

=+HH v (we use the expressions of the velocities u and v, as well as the same

property of the static moments), we obtain

dddd

O CC

CCCC

tttt

′

=×+ ×+×+× + +

wH wv vH

ρ , (16.3.51')

We can define the centres

E and I by the formulae

∑

ρρ

∑

ρρ

(16.3.52)

MECHANICAL SYSTEMS, CLASSICAL MODELS

()d

aa a

⋅

∫∫

rwn

()d

gg g

⋅

∫∫

rwn

ρ ,

454

analogous to the formulae (16.3.35). Noting that

=−

ρρρ

=−

ρρρ

and

taking into account (16.3.37), we get

()d ()d

aa a gg g

SSMμμ

⋅+ ⋅=−

∑∑

∫∫ ∫∫

rwn rwn H w.

In this case, the sums of the integrals in the formula (16.3.32) become

()d ()d

aaaa gggg

SSμμ

′′

×⋅+×⋅

∑∑

∫∫ ∫∫

ru w n ru wn

()

′

⎛⎞

′

=× − − × −

⎜⎟

⎝⎠

RvHw

()d ()d

aaaa gggg

SSμμ

+× ⋅+× ⋅

∑∑

∫∫ ∫∫

rw w n rw wn

()( )d ()( )d

aaaa gggg

SSμμ

+×× ⋅+×× ⋅

∑∑

∫∫ ∫∫

rrwn rrwnωω,

where we took into account the above result, the formula (16.3.31) and the expressions

of the position vectors

′

r and

′

r , as well the decomposition of the velocities

and

u . Replacing in (16.3.32) and taking into account the previous results and the relation

(16.3.51'), we get, finally,

=−×−

MwH

()d ()d

aaaa gggg

SSμμ

−× ⋅−× ⋅

∑∑

∫∫ ∫∫

rw w n rw w n

()( )d ()( )d

aaaa gggg

SSμμ

−×× ⋅−×× ⋅

∑∑

∫∫ ∫∫

rrwn rrwnωω

, (16.3.53)

where we have noticed that

′

=+×

MM R

To give to this equation of motion of rotation about the mass centre a form as useful

as possible from the point of view of the practical calculation, we mention that

∂

=+×

∂

ω ,

∂

=+×

∂

ω ,

(16.3.54)

where we have used the derivatives with respect to the non-inertial frame of reference

R. Noting that

=KIω , we have

16 Other Considerations on the Dynamics of the Rigid Solid

455

const const

CC C

tt t

∂∂ ∂

⎛⎞ ⎛⎞

⎜⎟ ⎜⎟

∂∂ ∂

⎝⎠ ⎝⎠



 

KK K

const

∂

⎛⎞

⎜⎟

∂

⎝⎠





ω ,

const

∂∂

⎛⎞

⎜⎟

∂∂

⎝⎠



ω ,

(16.3.55)

because the mechanical system

S is of variable mass.

We can decompose the resultant moment of the given forces in the form

CC C

=+MM M, where

M is the resultant moment of the forces of pressure

while

M is the resultant moment of the other external forces.

Noting that

()d

aa a

Sμ ⋅wwn and ()d

Sμ ⋅wwn can be considered

elementary forces due to

the capture of the particles of air and to the detachment of

particles of gas, respectively, through an elementary surface of area

dS, we introduce

the moment of traction in the form

()d ()d

aaaa gggg

SSμμ

=− × ⋅− × ⋅

∑∑

∫∫ ∫∫

MM rw wn rw wn.

(16.3.56)

As well,

const

()( )d

aaaaa

∂

⎛⎞

=− − × × ⋅

⎜⎟

∂

⎝⎠

∑

∫∫



rrwn

()( )d

gggg

Sμ

−×× ⋅

∑

∫∫

rrwnω

(16.3.57)

is the moment of gas-dynamical damping. The equation of motion (16.3.3) takes thus

the form

const

CC C C

∂∂

⎛⎞

+× = + − −× + − ×

⎜⎟

∂∂

⎝⎠



KM M KMwHωω

(16.3.58)

generalizing Euler's equations.

Considering that the aircraft is a system of constant mass and assuming that

t∂∂=K0, we can write

const

CC C

∂

⎛⎞

+× = + + ×

⎜⎟

∂

⎝⎠



KM MKωω

(16.3.58')

where the last term of gyroscopic nature corresponds to solid masses which give raise

to the spin. Comparing the equations (16.3.58) (where we make

t∂∂=K0) and

MECHANICAL SYSTEMS, CLASSICAL MODELS

456

(16.3.58'), we notice that, considering that the aircraft is a system of variable mass,

appears the supplementary moment

=+×MMHw

. (16.3.59)

Because the vectors

H and

w are, often, nearly parallel, it results

≅MM.

Hence,

=M0 if = 0ω ; the condition in which takes place a motion of translation

are thus formally the same, immaterial if the mechanical system

S is of constant or of

variable mass.

If we suppress the capture of particles of air, then the equation (16.3.58) becomes the

equation of motion of the rocket about the centre of mass.

16 Other Considerations on the Dynamics of the Rigid Solid

457

Chapter 17

Dynamics of Systems of Rigid Solids

A mechanical system S can be formed of a finite number (let be n) of rigid solids and

of a finite number (let be p) of particles, its position with respect to an inertial frame of

reference

′

R being specified by means of += +633(2 )np npparameters; hence,

such a system has

+3(2 )np degrees of freedom. In the case in which the system S is

subjected to m constraints, the number of degrees of freedom is reduced with m units,

equating

+−3(2 )np m. We study, in this chapter, the motion of the mechanical

system

S, free or with constraints, including the case in which appear discontinuities

(the collision problem). The results thus obtained will be applied to some problems of

dynamics of machines.

17.1 Motion of Systems of Rigid Solids

After some results with a general character, one considers the contact problem of two

rigid solids; in this order of ideas, one studies various particular cases too.

17.1.1 General Results

In what follows, we make some general considerations concerning the motion of

systems of rigid solids; a special attention is given to some particular cases (the double

pendulum and the sympathetic pendulum).

17.1.1.1 General Considerations

Let be, in general, a free mechanical system

S, formed of the rigid solids S

= 1,2,..., ,kn

and of the particles

P , of position vectors

′

= 1,2,...,ip

, with

respect to an inertial frame of reference

′

R , of pole

′

O ; the elements of this system

are acted upon by given external forces, originated in other systems, and by given

internal forces, corresponding to their reciprocal actions. The rigid solid

acts upon

the rigid solid

by a set of forces (analogously modelled as sliding vectors) of torsor

{

}

RM,

kl kl

, while the rigid solid S

acts upon the rigid solid S

by a set of forces

(analogously modelled) of torsor

{

}

RM,

lk lk

; corresponding to the theorem of action

and reaction (the Theorem 12.1.7 stated for a continuous mechanical system, can be

applied in the case of a system of rigid solids too), we can write

P.P. Teodorescu, Mechanical Systems, Classical Models,

459

{

}

RM,

kl kl

{

}

+=RM 0,

lk lk

, hence +=RR 0

kl lk

, +=MM 0

kl lk

, ≠kl,

=, 1,2,...,kl n

. The particles

P and

P are interacting with the forces F

(applied

upon the particle

P ) and F

(applied upon the particle

P ), respectively, having as

support the straight line

PP and verifying the relation +=FF 0

ij ji

, ≠ij,

=, 1,2,...,ij p; these forces are modelled as bound vectors. Analogously, if the rigid

solid

acts upon the particle

P with a force

Φ (modelled as a bound vector), then

the particle

P reacts upon the rigid solid S

with a force

Φ (modelled as a sliding

vector), these forces having the same support and verifying the relation

+=0

ik ki

ΦΦ ,

≠ik,

= 1,2,...,ip

= 1,2,...,kn

, as free vectors. As in the case of a discrete system

of particles (see Sect. 11.1.1.4 too), applying the principle of action of forces (the

theorem of torsor in case of a rigid solid; see Sect. 14.1.1.7 too), we can write the

equations of motion of the free mechanical system

S in the form (for the sake of

simplicity, it is convenient to denote by “prime” the sums of terms with two indices, if

the case of equal indices is excluded)

=+ +

∑∑

rF F

ii ij



Φ , = 1,2,...,ip,

(17.1.1)

′

=+ +

∑∑

HR R

k k ki kl



, = 1,2,...,kn,

′′

=+×+

∑∑

KM r M

ki kl

Ok Ok



, = 1,2,...,kn,

(17.1.1')

where

is the resultant of the given external forces which act upon the particle

P ,

{

}

′

RM,

is the torsor of the given external forces which act upon the rigid solid

, while

′

and

′

represent the momentum and the moment of momentum,

respectively, of the rigid solid

, with respect to the pole

′

O , in the frame of

reference

′

. In general, the given forces can depend on the position vectors

′

= 1,2,...ip, on the position vectors

′

and on Euler’s angles

ψ ,

θ ,

ϕ , which

specify the position of a point of the rigid solid

, = 1,2,...,kn, as well as the

motion of rotation about this one.

The mechanical system

S is considered to be free, so that the +2np vector

equations (17.1.1), (17.1.1') (or, in components, the

()

+32np scalar corresponding

equations) can determine the

()

+32np parameters (co-ordinates and Euler’s angles),

which specify its position. These equations are completed by the initial conditions (at

the moment

tt), i.e.: the positions and the velocities of the particles, as well as the

positions and the velocities (the parameters which specify them) of the rigid solids

which form the mechanical system

S. In this case too, starting from the Theorem

11.1.1, corresponding to a system of particles, and taking into account the Theorem

14.1.12, corresponding to a rigid solid, we can state a theorem of existence and

MECHANICAL SYSTEMS, CLASSICAL MODELS

460

uniqueness of Cauchy-Lipschitz type for the free discrete mechanical system considered

above.

In the case of a mechanical system

S subjected to constraints (external or internal,

because of the contact between the rigid solids or because of other causes), one must

introduce also the constraint forces (external or internal). If a particle

∈ S

P , e.g., is

constrained to move on a surface

∈ SS , then the constraint is internal, while if

∉ SS , then the constraint is external. Analogously, if a rigid solid ∈ S

S remains

in contact with another rigid solid appears a torsor of internal or external constraint

forces, as this solid belongs or not to the mechanical system

S. The holonomic

constraint relations are of the form

() () ()

()

′′′′ ′ ′

123

,,,,,,,,;0

kkk

iii

kk k

OOO

fxxxx x x t

ZRK

= 1,2,...,qB

(17.1.2)

the non-holonomic constraints being expressed by the relations

() () () () () ()

(

() () ()

′′′′′′′ ′ ′

123123

123

,,,,,, , ,

kkk

iiiiii

OOO

gxxxxxxx x x

 ,

() () ()

)

′′′

123

, , ,,,,,,; 0

kkk

kk k kk k

OOO

xxx tZRKZRK



 

, = 1,2,...,rC ,

(17.1.2')

linear in the linear and angular velocities. Obviously, the number of the unknowns

increases by

=+mqr, corresponding to the constraint forces; but also the number of

relations which link the unknown functions increases analogously (by the relations

(17.1.2), (17.1.2')). We can enounce a first basic problem (the direct problem), the

solution of which is unique in certain conditions, sufficiently large (e.g. the Cauchy-

Lipschitz theorem). A second basic problem (the inverse problem), as well as the mixed

basic problem have not, in general, a unique solution; to have uniqueness, it is

necessary to impose some supplementary conditions (see Sect. 11.1.1.4 too).

17.1.1.2 The Double Pendulum

The double pendulum is a mechanical system

S formed of two rigid solids S

and

, subjected to the action of the own weights =Gg

M and =Gg

M at the

centres of mass

C and

C , respectively; the rigid solid S

oscillates about a fixed

horizontal axis

′

Ox , while the rigid solid S

oscillates about an axis

Ox , parallel

to the first axis and rigidly connected to the solid

. We assume, for the sake of

simplicity, that the vertical plane normal to these axes, which passes through the poles

O and

O , is a plane of geometric and mechanical symmetry for the mechanical

system

S, hence containing also the mass centres

and

; we assume that

∈

112

COO

too. We choose the

′

Ox -axis along the descendent vertical, the

′

Ox -axis

being horizontal; the axes

and

are chosen analogously. The position of the

system

S (the motion is plane-parallel, the point

O is fixed (two constraint relations),

while the point

O is moving on a fixed circle (one constraint relation), hence the

mechanical system has

()

⋅− + =23 2 1 3degrees of freedom) is specified by the

17 Dynamics of Systems of Rigid Solids

461

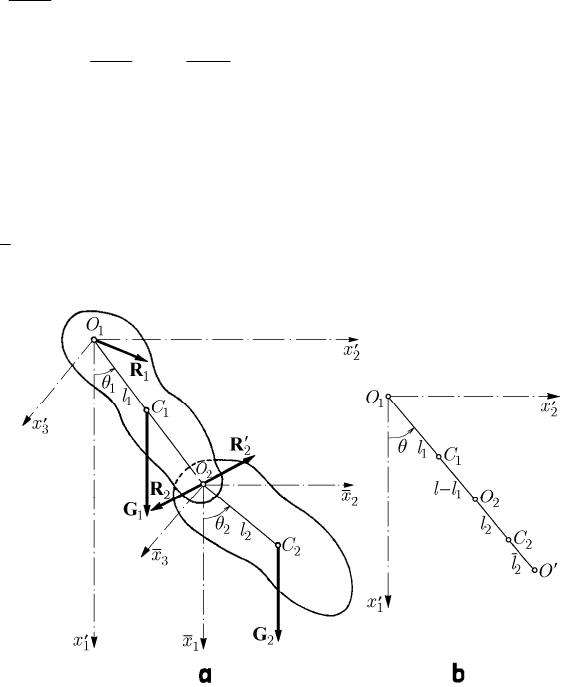
MECHANICAL SYSTEMS, CLASSICAL MODELS

distance =

OO l between the two poles (constant for a given double pendulum) and

by the angles

R and

R made by

OC and

OC , respectively, with the descendent

vertical; we notice

11 1

OC l , =

22 2

OC l too (Fig. 17.1,a). Upon the rigid solid S

act

the own weight

=Gg

M , the constraint force R

O and the constraint force R

exerted by the rigid solid

upon the rigid solid S

at the cylindrical hinge

O , while

upon the rigid solid

act the own weight =Gg

M and the constraint force

′

exerted by the rigid solid

upon the rigid solid S

O ; obviously, we

have

′

RR 0

. We neglect the friction couples which appear on the axes

′

and

Ox . The motion of both centres of mass is given by the equation (the

differentiation takes place with respect to the fixed frame of reference)

Fig. 17.1 Double pendulum

=++gR R

11 1 1 2



ρ ,

′

22 2 2



ρ ,

where

()

′′

11 11 12

cos sinl RR

()()

′′

=+ ++

212211222

cos cos sin sinll llRR RRρ

are the corresponding position vectors; projecting on the axes

′

Ox ,

′

Ox and

calculating the components of the accelerations, one obtain the components of the

constraint forces in the form

()

=− + +

11 1 1 2 1 1 1 1

cos sinRMlMlRR RR



()

−+−+

22 22 22 1 2

cos sinMl M M gRR RR



()

()( )

=+ − + −

12 1 1 2 1 1 1 1 2 2 2 2 2 2

cos sin cos sinRMlMl MlRR RR RR RR

   

(17.1.3)

462

()( )

′

=− = + + + +

ªº

¬¼

21 21 2 11 11 2 22 22

cos sin cos sinRRMl l gRR RR RR RR

 

()( )

′

=− =− − + −

ªº

¬¼

22 22 2 1 1 1 2 2 2 2 2

cos sin cos sinRRMl lRR RR RR RR

   

(17.1.3')

Taking into account the Huygens-Steiner theorem (formulae (3.1.113), (3.1.113'), we

can write the moment of inertia of the rigid solid

with respect to the

′

Ox -axis in

the form

()

11 1

Ml i , where

i is the gyration radius corresponding to the mass

centre

C , taken with respect to an axis parallel to

′

Ox ; the moment of inertia of the

rigid solid

with respect to an axis parallel to the

Ox , which passes through the

mass centre

C , is given by

Mi , where

i has an analogous significance. The

theorem of moment of momentum for the rigid solid

, in the frame

′

R , with

respect to the

′

Ox -axis, reads

()

+=− + −

11 1 1 11 1 22 1 21 1

sin cos sinMl i Mgl lR RRRRR



As well, writing the theorem of moment of momentum for the rigid solid

, in a

frame of reference of Koenig, with respect to an axis parallel to the

′

Ox -axis, we get

()

′′

=−

22 2 2 21 2 22 2

sin cosMi l R RRRR



Replacing the constraint forces given by (17.1.3'), it results the system of differential

equations of second order

() ()

+−−−+ =

11 2 1 2 2 1 2 1

cos sin sin 0

BR R R R R R R C R

  

() ()

+−+−+ =

22 2 1 1 2 1 1 2

cos sin sin 0

BR R R R R R R R

  

(17.1.4)

where

()

22 2

li l

B ,

To determine the motion, one must add also the conditions

()

10 1

tRR,

()

20 2

tRR,

()

10 1

tRR



()

20 2

tRR



, where

R ,

R and



specify the

position and the velocity, respectively, of the double pendulum at the initial moment.

Being impossible to give an exact solution to this non-linear problem, we will

consider the case of small motions for which

()

−≅

cos 1RR , ≅

sin RR,

≅

sin RR and

()

−≅−

21 21

sin RR RR; we find thus

()

+− − + =

11 2 2 1 2 1

BR R R R R CR

  

()

22 1 2 1 1 2

BR R R R R R++ − + =

  

(17.1.4')

17 Dynamics of Systems of Rigid Solids

463