Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems
Подождите немного. Документ загружается.


ends of the axle of the flywheel are sustained by a reinforcement which is rotating about
the axle
AOA
′
, which is transversal to the ship (Fig. 16.32); at the bottom of the
reinforcement is put a weight
G, so that – in the normal position – the
3
Ox
-axis be
vertical. If, under the action of the waves, the steamer is inclined and rotates about the
longitudinal axis
3
Ox
′
with the angular velocity
′
ω
(motion of rolling), then arises a
gyroscopic moment
g
M
,
of magnitude
3
I ωω
′
, which imparts to the flywheel a rotation
about the axle
AOA
′
(motion of pitching); this leads to a new gyroscopic moment
g
′
M
which, by means of the bearings
A and A
′
, is in opposition to the motion of pitching,
diminishing thus the inclination of the ship about its longitudinal axis. This gyroscope
proves its utility in the rectilinear motion of the steamer, as well as in the case of the
rotations about the vertical line in the same sense as its rotation; in the case of a rotation
in an opposite sense, take place supplementary motions of pitching, which can be
dangerous. For this reason, there have been invented and built also other anti-pitching
gyroscopes much more perfected, used to stabilize the steamers (e.g., the Sperry
gyroscope); in this order of ideas, we mention the pilot gyroscope too, which
determines the motion of precession.
Fig. 16.32 Schlick’s gyroscope
The stabilization of the cars with only one rail (monorail) is analogously realized.
The gyroscope with a vertical axle considered by Scherl to this purpose is analogous to
Schlick's gyroscope. Brennan has introduced a gyroscope with a horizontal axle, useful
in case of a rectilinear motion. To increase the precession, other auxiliary apparatuses
are used. We mention also the realization of the monorail coach, of the gyroscopic
motorcar on two wheels and of the gyroscopic bicycle with only one wheel.
The motion of the bicycle with two wheels is also stabilized by the gyroscopic
moments which appear. If the linear velocity is
v, then the angular velocity is given by
/vrω = , where r is the radius of the wheel. Assuming that, for some reason, the
bicycle is inclined with an angular velocity
′
ω
, arise the gyroscopic moments
16 Other Considerations on the Dynamics of the Rigid Solid
433
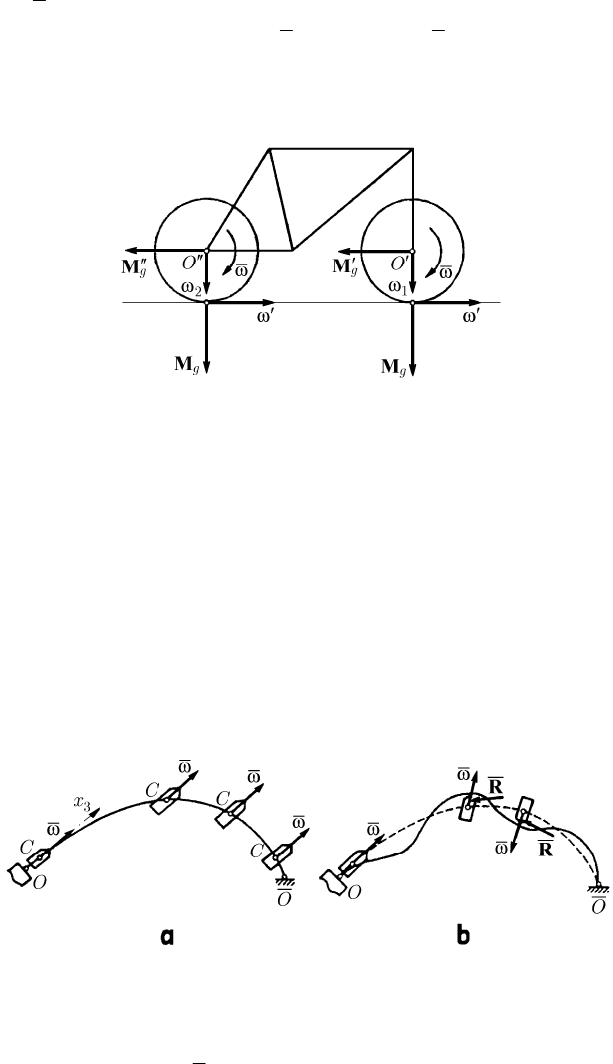
3
g
I
′
=×ωωM , to which correspond the angular velocities
1
ω and
2
ω , which lead to
the new gyroscopic moments
31
g
I
′
=×ωωM ,
32
g
I
′′
=×ωωM , of a sense opposite
to that of
′
ω
(Fig. 16.33); these moments tend to bring back the bicycle in the vertical
position, stabilizing its motion. Obviously, this modelling of the phenomenon is
approximate; the problems which arise are multiple and much more difficult.
Fig. 16.33 The bicycle with two wheels
We meet applications of the gyroscopic effect also in case of mills with movable
pulleys, of pendulary mills or in case of other mills used to grind cereals, grains or other
materials.
As we have seen in Sect. 16.2.2.3, the gyroscope can be used successfully also as an
orientation device. Thus, the gyroscopic compass, with the mobile axle in the local
horizontal plane is used to determine the direction north-south in the motion of ships
and, especially, of submarines. The azimuth gyroscope (with the mobile axle in the local
meridian plane) is used to determine the latitude at the respective position on
the surface
of the Earth. As well, a heavy gyroscope, with the fixed point over the centre of gravity,
allows to determine the gyroscopic horizon (the artificial horizon), even when – on the
sea – this one is in a thick fog; the gyroscopic inclination compass determines the
inclination with respect to the horizon of the longitudinal axis of an aircraft, as well as
of its transverse axis.
Fig. 16.34 Motion of a projectile. Constant direction of it (a). Screw motion of its vertex (b)
We meet gyroscopic effects which must be taken into consideration in ballistics too;
thus, a projectile, besides the motion of its centre of gravity
C, has also a motion of
rotation of angular velocity
ω
about its axis of symmetry
3
Ox . If the motion takes
MECHANICAL SYSTEMS, CLASSICAL MODELS
434
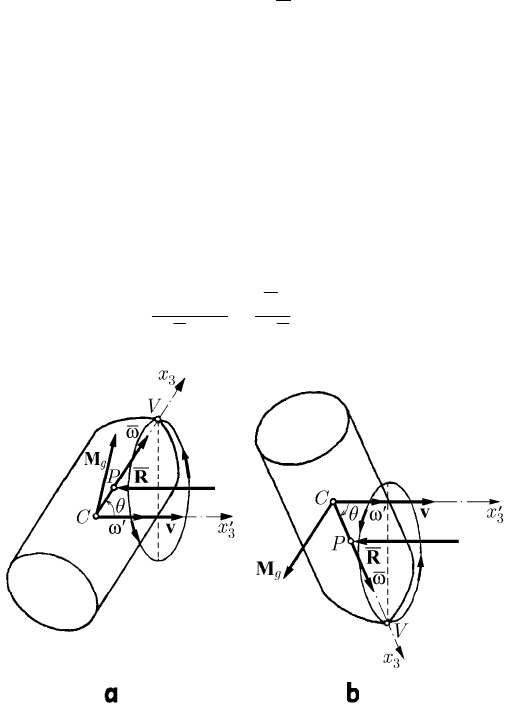
place in vacuum or in the air of resistance
R , passing always through C, we have
O
=M0
, so that the
3
Ox
-axis does not change its direction (Fig. 16.34a); the axis of
the projectile moves away from the
tangent to the trajectory and comes up against a
resistance of the air more and more greater, while the target is reached with the inferior
part of the projectile. In reality, the resistance of the air
R does not pass through the
centre
C, but through a point P at the distance l from C; we assume that this resistance
is approximately parallel to the velocity
v of the centre of gravity. There appears a
gyroscopic moment
g
M
applied at C, normal to the plane of the trajectory, which leads
to a motion of precession of the projectile about the vector
v with an angular velocity of
magnitude
33
sin
g
M
Rl
II
ω
ωθ ω
′
==
.
(16.2.40)
Fig. 16.35 The direction of the vertex of a projectile: upwards (a) or downwards (b)
Thus, the vertex
V of the projectile is directed upwards (Fig. 16.35a) and then
downwards (Fig. 16.35b); the vertex of the projectile tends to the tangent to the
trajectory (the projectile runs after its tangent). In the real motion, the projectile vertex
describes a screw motion around the trajectory of its centre of mass (Fig. 16.34b). By a
convenient choice of the form and of the dimensions of the projectile, the point
P will
be situated between the points
C and V, the angle remaining sufficiently small, so that
the projectile be falling with its vertex.
An important rôle is played by the directional gyroscopes, e.g., by those used to
maintain the direction of the automobile torpedo; we mention also the automatic
directional gyroscopes (e.g., the gyropilot). We put in evidence the navigation by
inertia and the gyroscopic directing of the rockets, useful for the guided rockets, the
intercontinental rockets and the interplanetary rockets.
16 Other Considerations on the Dynamics of the Rigid Solid
435
16.3 Dynamics of the Rigid Solid of Variable Mass
We take again the problem of dynamics of the mechanical systems of variable mass by
some considerations concerning
the application of variational methods of calculation;
we apply then these methods to some particular cases of motion. As well, we consider
the case of the aircraft fitted with jet propulsion units.
16.3.1 Variational Methods of Calculation
In the following we present firstly the approximate variational methods of R. Goddard
and H. Oberth, passing then to considerations concerning the general methods of
calculation with a variational character. We will assume a particle model of the rigid
solid, using the results obtained in Chap. 10, Sect. 3.
16.3.1.1 Goddard’s Approximate Method
Let us consider the rectilinear motion of a particle of variable mass in a gravitational
field, with a resistance of the medium
(, )vx=QQ , where v is the velocity along the
Ox-axis; the equation of motion, corresponding to the equations obtained in Chap. 10,
Sects. 3.1.2 and 3.2.3, reads
sin ( , )mv mg Q v x mwθ=− − −
,
(16.3.1)
Fig. 16.36 Goddard’s approximate method of calculation
where
w is the relative velocity of the emitted mass with respect to a non-inertial frame
of reference rigidly linked to the particle in motion while
θ is the angle made by the
trajectory with the horizontal line (Fig. 16.36). Taking the mass of the form (10.3.11')
and putting
0
(, ) (, )Qvx m vxϕ= , we may write
sin
f
vfg gfwθϕ=− − −
,
(16.3.1')
finding thus solutions of the form
1
(; , ; )vvtffC=
,
12
(; , ; , )xxtffCC=
, where
12
,CC are integration constants; these solutions can be taken as functional equations of
some problems of optimization, where various characteristics of the motion (the
distance travelled through, the time in which a certain position can be reached, the work
and the resistance of the medium) take extreme values. In 1919, R. Goddard proposed
an approximate solution to determine the function
()vvx= , so as to reach a given
MECHANICAL SYSTEMS, CLASSICAL MODELS
436

height with a minimal mass; the total height is divided in
n parts and on each part the
resistance of the medium is considered to be constant (
constϕ =
). As well, one
assumes that
/2θπ= ,
constva==
, obtaining an equation of the form (10.3.13')
with constant coefficients
0
g
ag
ff
ww
ϕ
+
++=
.
(16.3.2)
The solution (10.3.13") of this equation leads to
{
}
[( )/ ] [( )/ ]
0
() e e
ag wt ag wt
g
m
ft C
mag
ϕ
−+ +
== −
+
,
(16.3.2')
with
1/()Cgagϕ=+ + (we notice that (0) 1
f
= ). If the mass used up at a given
moment is
0
mm− , hence if
00
1( )/
f
mmm=− − , then it results
{}
0
[( )/ ]
0
11e
ag wt
mm
g
mag
ϕ
−+
−
⎛⎞
=+ −
⎜⎟
+
⎝⎠
,
(16.3.2'')
Imposing, together with Goddard, that that the final mass be equal to unity (
1m = ),
we get
{}
[( )/ ] [( )/ ]
0
e1e
ag wt ag wt
Q
m
ag
++
=−−
+
.
(16.3.3)
To
0Q = and 0g = corresponds
(/ )
0
e
awt
m
∗
= , so that the problem of extremum
of the mass, in the given conditions, consists in minimizing the ratio
(/ )
00 0
/e
awt
mm m
∗−
= .
The calculation is made successively for each of the
n intervals, till the final mass
equates the unity. Thus, we obtain also the time in which the displacement takes place
and which corresponds to the minimum of the ratio of the masses.
16.3.1.2 Oberth’s Approximate Method
For the same problem, H. Oberth assumes in 1929 that the velocity of the particle is
negligible with respect to the relative velocity of emission of the mass of combustible
(
vw
); denoting m=+RQ g, it results the equation of motion along the
ascendent vertical (Fig. 16.37)
mv R mw=− −
. (16.3.4)
We notice that
(d /d )vvxv=
, (d /d )mmxv= , so that we can also write
dd
0
dd
vR m
mw
xv x
++ =
.
(16.3.4')
16 Other Considerations on the Dynamics of the Rigid Solid
437

If at the height
x we impose a condition of minimal consumption of combustible
(
d/d 0mx= ) and if we differentiate the equation (16.3.4') with respect to v, then we
get
()()
d
0
d
vR
m
vxvv
∂∂
+=
∂∂
.
Fig. 16.37 Oberth’s approximate method of calculation
In the hypothesis
dconstmv= , it results
() ()
0
RmgQ
vv v v
∂∂+
==
∂∂
,
(16.3.5)
where the force
R is opposed to the motion ( /Rv is the resistance on unit of path and
time). One obtains thus the optimal velocity to raise a particle of variable mass (for
which the unit loss caused by the force
R is minimal). We have seen in Chap. 10,
Sect. 3.2.5 that the resistance can be taken in the form
2
() /2Qv bAvρ= , where
()bbv= is the aerodynamic coefficient, ρ is the density of the air, while A is an area
characteristic for the rigid solid modelled as a particle (in case of the aircraft, the area of
the wing). If we assume that
constm = on a stratum of width dx, then the relation
(16.3.5) leads to
2
11d
0
22d
mg b
bA Av
v
v
ρρ−+ + =,
wherefrom
2
2
[(/)]
mg
v
Ab v db dvρ
=
+
.
(16.3.6)
Taking
constb = , it results
2mg
v
bA
ρ
= .
(16.3.6')
MECHANICAL SYSTEMS, CLASSICAL MODELS
438

Hence, if the resistance of the medium
()Qv is in direct proportion to the square of
the velocity, then it will be equal to the weight of the particle (
Qmg=
); in this case,
the optimal velocity of the rigid solid of variable mass is the velocity which must have
the particle of mass
m in free falling in a homogeneous medium of given density ρ.
From the above results, one obtains easily all the kinematic and dynamic characteristics
of the motion.
16.3.1.3 General Considerations on the Application of Variational
Methods of Calculation
The methods of calculation of Goddard and Oberth have an approximate character; we
give a formulation of the same problem, in what follows, in a rigorous variational
calculus. We have seen in Chap. 7,
Sect. 2.1.4 that, in case of a functional
12
( , ,..., )
n
Iy y y of the form (7.2.13) for the functions ()
k
yx, 1,2,...,kn= , of the
same independent variable
x, we are led to the Euler-Lagrange equations (7.2.13').
Imposing the supplementary conditions
12 12
( ; , ,..., ; , ,..., ) 0
nn
j
f
xy y y y y y
′′ ′
= , 1,2,...,jh= ,
(16.3.7)
too, we introduce the auxiliary function
1
h
j
j
j
FF fλ
∗
=
=+
∑
,
(16.3.7')
where
12 12
( ; , ,..., ; , ,..., )
nn
FFxyy yyy y
′′ ′
= is the function under the integral operator
in the functional (7.2.13), while
()
jj
xλλ= , 1,2,...,jh= , hn< , are Lagrange’s
multipliers which must be determined; the equations (7.2.13') lead to
()
d
0
d
k
k
y
y
FF
x
∗∗
′
−=, 1,2,...,kn= ,
(16.3.7'')
,
k
k
y
y
FF
′
being the partial derivatives with respect to the corresponding arguments (
k
y
and
/
kk
yyx
′
=∂ ∂ ). We obtain thus a system of n differential equations (16.3.7") and a
system of
h non-holonomic constraint relations (16.3.7) for the n functions
12
, ,...,
n
yy y and for the h parameters
12
, ,....,
h
λλ λ.
In our case, the problem of determination of the law of variation of the particle mass
is put, so that the path travelled through
00
dd
xT
xvt=
∫
∫
have a maximum, T being the
time in which the motion of the particle takes place, while
X is the space travelled
through. In this variational problem the function
v under the integral must verify the
differential equation of the particle of variable mass (16.3.l') on the active segment
[
]
1
0,t (till the end of the process of emission, hence of combustion of a rocket) and the
differential equation of the particle of constant mass (
11
()mmt= ,
11
()
f
ft= )
16 Other Considerations on the Dynamics of the Rigid Solid
439
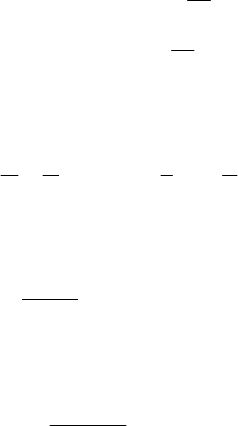
11
sin
f
vfg gθϕ=− −
, (16.3.8)
on the passive segment
[
]
1
,tT. To apply the general method of calculation, we
assume, after A.A. Kosmodemyanski, some simplifying hypotheses. Thus, we consider
that, on the active segment, the consumption of mass on a second is a finite magnitude,
being negligible on the passive segment; thus, the function
f, partially continuous on the
interval
[
]
0,T
, is replaced by a continuous function, sufficiently close to that one. In
what concerns the condition (16.3.8), we can have any velocity at the initial moment, as
well as any value for
1
0
f
> ; hence, this condition may be overlooked in the
variational problem which was put, remaining with the condition (16.3.1'), written in
the form (
d/dvvvx=
, d/d
f
vf x=
)
sin ( , ) 0
xx
f
vv fg g v x vwfθϕ
′′
++ +=
.
(16.3.8')
In our case,
1F = , while
1
()yfx= ,
2
()yvx= , so that
[
]
1sin(,)Ffvvfggvxvwfλθϕ
∗
′′
=+ + + +
.
The equations (16.3.7") lead to
d
()()0
d
v
fv g wf vw
x
λϕ λ
′′ ′
++ − =
,
d
(sin)()0
d
vv g vw
x
λθλ
′
+− =
.
Developing and eliminating
λ and
x
λ
′
between these equations, we get
() sin0
v
f
vgg
vw
f
wfw
ϕθ
′′
⎛⎞
′
+−−+ =
⎜⎟
⎝⎠
.
Eliminating the sum
//
f
fvw
′′
+ between this relation and (16.3.8'), we obtain
[]
1
()
sin
v
fvwvw
w
ϕϕ
θ
′
=−+
.
(16.3.9)
Taking
2
0
() () /2vbvAv mgϕρ= , as in aerodynamics, we can write
[]
2
0
()
2sin
v
Av
mmf vwbvwb
gw
ρ
θ
′
== ++
,
(16.3.9')
where we assume, usually, that the gravity acceleration does not
-
vary with the altitude;
we have thus determined the relation between the mass and the velocity of the particle
in case of an optimal regime. In the hypothesis in which
constb =
, the relation
(16.3.9') is reduced to
MECHANICAL SYSTEMS, CLASSICAL MODELS
440

(
)
2
1
2sin
Abv
v
m
gw
ρ
θ
=+
,
(16.3.10)
while, in case of the motion on the vertical, it results
(
)
2
1
1
2
v
mg Abv
w
ρ=+
.
(16.3.10')
If
vw , then we find again Oberth’s formula.
16.3.2 Applications to Dynamics of the Rigid Solid of Variable Mass
Using again the modelling as a particle of the rigid solid of variable mass, we apply the
above results to the study of the motion in a homogeneous atmosphere and of the
motion by simultaneous capture and emission; as well, we make some considerations
concerning
-
the motion of the rocket.
16.3.2.1 Motion in a Homogeneous Atmosphere
In 1946, A.A. Kosmodemyanski dealt with the motion of the particle of variable mass
in a homogeneous atmosphere (
constρ = ), using the above considerations. Noting
that
d/d
f
vf x=
, the equation (16.3.1') reads
()
[
]
sin ( )
v
f
wf v g f vθϕ
′
+=− +
.
(16.3.11)
In this case, the length of the path travelled through the rectilinear trajectory is given by
[]
0
00
()d
d(;,)d
sin ( )
TV V
v
v
v
f
wf v v
vt Fvf f v
gf vθϕ
′
+
′
==−
+
∫∫ ∫
,
(16.3.12)
where
0
v
is
the initial velocity.
Writing the Euler-Lagrange equation corresponding to this functional, we get
2
( sin ) ( ) sin
d
0
dsin
(sin )
v
vf f wf v
vw
vf
f
θϕ θ
θϕ
θϕ
′
+−+
−=
+
+
,
being thus led to the relation (16.3.9) in the particular case in which
constg = and
()vϕϕ= .
The relation (16.3.11) allows to write
[]
0
d
sin ( )
v
v
v
f
wf
tv
gf vθϕ
′
+
=
+
∫
,
(16.3.13)
where
()
f
v is given by the relation (16.3.9); we obtain thus the velocity ()vvt= .
Associating the relation
()
f
fv= too, we determine the variation law of the particle
mass, hence the optimal regime of work of the motor, in case of a rocket.
16 Other Considerations on the Dynamics of the Rigid Solid
441

16.3.2.2 Motion by Simultaneous Capture and Emission
Let be a particle of variable mass which is moving in the same conditions as above in a
uniform gravitational field, with the initial condition
0
(0)vv= . In the case of a
phenomenon of simultaneous capture and emission, the differential equation of motion
is of the form
0
sin ( ) ( ) ( )mv mg m g v m u v m u vθϕ
−+
−
+
=− − + − + −
,
(16.3.14)
where
0m
−
< and 0m
+
> correspond to the variations of the emission and of the
capture of mass, while
u
−
and
u
+
are the absolute velocities, respectively. Denoting by
wuw
−−
=−
the relative velocity – considered to be constant – of the emitted masses,
with respect to the non-inertial frame of reference, assuming that
0u
+
= (case
considered by Levi-Civita) and that
/mmγ
+−
=−, we also can write
[]
sin ( )
v
mv mg v m wθϕ
γ
−
−
⎛⎞
=− + + +
⎜⎟
⎝⎠
.
(16.3.14')
Because
constw
−
= at the end of the active segment (
1
tt= ), when 0u
−
= , we
have
1
wv
−
= , where
1
v is the velocity at the respective moment.
If we denote
0
() ()mt mft
−
= , with (0) 1
f
= ,
0
(0)mm
−
= , then it results
0
(1 1/ ) (1 1/ )mm m m mfγγ
−+ −
=+= − = −
, because
0
() ()mt m m t
−
=+
()mt
+
+ ; we get thus
[
]
0
() ()mt mbft a
+
=− + and
[
]
0
() ()mt m af t b=+,
11/a γ=− , 1/b γ= , 1ab+=. Replacing in the equation (16.3.14'), we obtain
[
]
1
() ()sin ( )af b v g af b f v bvθϕ+=− + +− −
.
(16.3.14'')
Choosing
v as independent variable, we can write
[
]
[]
00
11
1
( ) () ()
(;, )d d
() sin ()
vv
v
v
vv
vbvfvafvbv
gx F v f f v v
af v b vθϕ
′
−++
′
==
++
∫∫
.
(16.3.15)
We impose a variation of mass given by
()
f
v , so that the displacement x have a
maximum. Writing the corresponding Euler-Lagrange equation, we get
[
]
111
1
()()(2) ()(2)sin
()
(2)sin
v
vv bv v a bv v v bv bv
fv
av bv
ϕϕθ
θ
′
−++−−−
=
−
.
(16.3.16)
As well, starting from the same relation (16.3.14"), we can write
[]
1
1
( ) () ()
d
() sin ()
v
v
v
vbvfvafvb
gt v
af v b vθϕ
′
−++
=
++
∫
.
(16.3.15')
MECHANICAL SYSTEMS, CLASSICAL MODELS
442
