Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

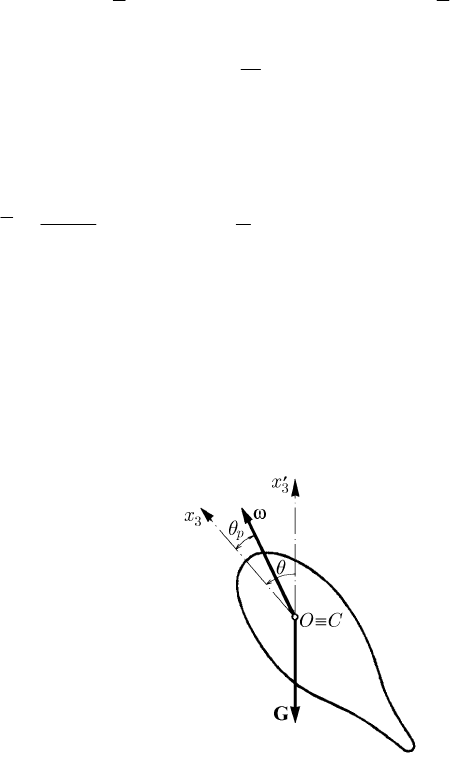
16 Other Considerations on the Dynamics of the Rigid Solid

(obviously,

ωω= , the magnitude of the angular velocity being constant). Noting

that

=M0, the formula (15.2.17') leads to the relation

()

/cos 0IJIωω θ

′

−− =. Eliminating the ratio /ωω

′

, these results lead to

tan tan

θθ=

(16.2.5)

so that we can determine the position of the fixed axis

′

in the plane formed by the

Ox -axis and the initial angular velocity

ω . We obtain, as well,

cos

ωωθ

−

()

1/2

22 2 2

sin cos

ωθθ

′

(16.2.5')

the last relation corresponding to the first relation (16.2.2). Hence, if to a heavy

gyroscope, hanged at its centre of gravity, one gives an initial rotation about an axis

inclined with the angle

θ with respect to its axis, then the gyroscope becomes a motion

of precession about a fixed axis situated in the plane determined by its initial position

and by the axis of initial rotation and which makes the angle

θ (specified by the formula

(16.2.5)) with the initial position. We must notice that the fixed axis (the

′

-axis) is

not necessarily vertical.

Fig. 16.13 The motion of the gyroscope acted upon by its own

weight G and for which

OC≡

The first formula (16.2.2) gives

′

, while the second formula leads to 0δ = ;

hence, the moment of momentum

′

K is directed along the fixed axis

′

. Indeed,

from the theorem of moment of momentum it results

′



, hence

′

K has a fixed

direction in space; but this vector is contained in the

Ox x

′

-plane, which has only one

fixed direction, i.e.

′

403

In the particular case in which

θ = it results 0θ = , 0ω

′

= , ωω= , while the

′

-axis will coincide with the

Ox -axis; we are in the case considered in Sect.

16.2.1.1.

16.2.1.3 The Motion of Regular Precession of a Heavy Gyroscope

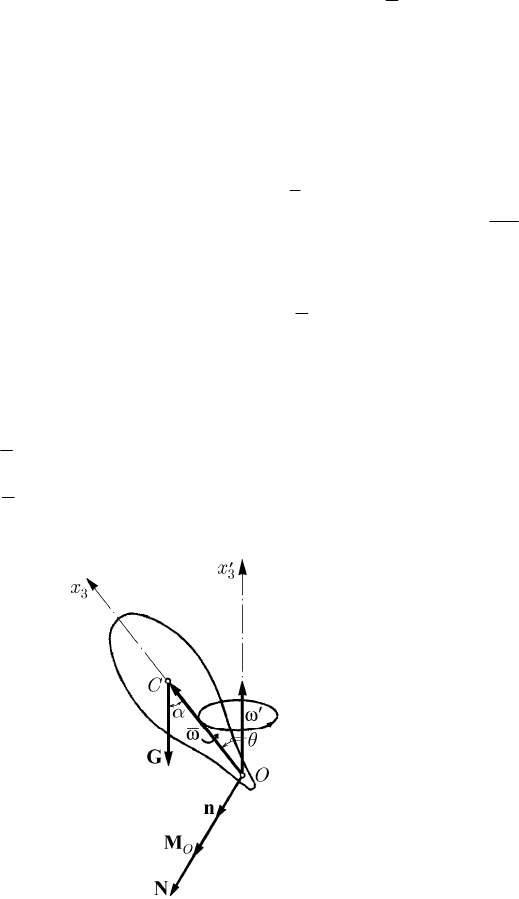
Let be a gyroscope of weight G, having the fixed point O situated on the symmetry axis

Ox , subjected to a proper rotation of angular velocity ω . The moment of the given

external forces is

OC=×

JJG

MG, of magnitude sin

MGlα= , where lOC= ,

while

α is the angle made by the

-axis with the vertical line (Fig. 16.14) (we are in

the Lagrange-Poisson case). To obtain a motion of regular precession (

constω

′

= and

constθ = ), together with a uniform proper rotation ( constω = ), we must have

const

M = , in conformity to the formula (16.2.3'), wherefrom it results constα = .

The support of the vector

M must be, during the motion, normal to the

Ox x

′

-plane

(along the line of nodes), corresponding to the formula (15.2.17'); it describes a

horizontal plane, the

′

-axis being thus vertical and αθ= . At the initial moment,

the angular velocities

ω and ω

′

must verify the condition

()

cosIIJ Glωω ω θ

′′

+− =,

(16.2.6)

Fig. 16.14 The motion of the gyroscope with a progressive precession

MECHANICAL SYSTEMS, CLASSICAL MODELS

404

16 Other Considerations on the Dynamics of the Rigid Solid

′

(16.2.6')

which specifies the angular velocity

′

; this formula is exact if /2θπ= . If these

initial conditions do not hold, then a supplementary motion of nutation (

constθ ≠ )

appears. In general,

()

33 3

4cos

2cos

II GlIJ

ωωωθ

⎡

⎤

′

=±+−

⎣

⎦

−

(16.2.6'')

obtaining two values for the angular velocity

′

, with the condition

()

2/ cosIJIGlωθ>−, if

JI>

; if

JI<

then the quantity under the

radical is always positive (we assume that

cos 0θ >

Practically, it is difficult to obtain angular velocities which fulfil the above

conditions; as well, the frictions and the resistance of the air have an influence on the

angular velocities

ω and

′

, which can remain constant only with a certain

approximation.

In the case considered in Fig. 16.14 (

JJG

has the same sense as ω ), the moment

is directed in the positive sense of the ON-axis, the precession being progressive

(such a gyroscope can be, e.g., a top, as that in Fig. 16.7b, but with an axis inclined with

respect to the vertical line). If the fixed point

O is on the other part of the mass centre

C, so that ω has an inverse sense with respect to OC

JJG

, then the angular velocity

′

directed in a opposite sense with respect to the

′

-axis and the moment

M has a

sense opposite to that of the

ON-axis; thus the precession is retrograde. The gyroscopic

balance allows to put in evidence this phenomenon. If, on the

-axis, on one part of

the fixed point

O we have a gyroscope of weight G (the symmetry axis of the

gyroscope is along

Ox ) and if on the other part acts a weight P (which can glide along

the axle), then the centre of gravity

C, were acts the force +GP, will be on one part

or on the other one with respect to the point

O; thus, the motion of precession about the

fixed vertical axis

′

can change its sense.

corresponding to the condition (15.2.11), to can obtain the wanted motion. In the case

in which

/1ωω

′

 or in the case in which

()

/1IJI−  , we get the

approximate formula

405

Fig. 16.15 The motion of the gyroscope for which the resultant R is

applied at Q on the symmetry axis

More general, if the resultant of the given external forces to which is subjected the

gyroscope is a force

R applied at the point Q on the symmetry axis, inclined by the

angle

α with respect to the

Ox -axis (Fig. 16.15), then we obtain

OQ=×

JJG

MR and

sin const

MRlα==

, where lOQ= . Making the same considerations as in the

preceding case, we obtain analogous results; thus

αθ=

, with the only difference that

the

′

-axis is not necessarily vertical, but is parallel to the resultant R. If the angular

velocity

ω is sufficiently great, the velocity

′

is given, with a good approximation,

by the formula (16.2.6'), the angle being practically constant. For an illustration of these

results, we present the experiment of Charron. In this case, the

Ox -axis of the

gyroscope is formed by a magnet

NS, the point O being the pole S (Fig. 16.16). We

bring close to the pole

N a horizontal magnet m with a pole P; if the gyroscope is

immobile, then to can attract the pole

N it is necessary that the pole P be a south pole. If

we impart to the gyroscope an angular velocity

ω and if we bring near the pole N the

magnet with the pole

P as north pole, then we see that the point N of the gyroscope

comes close to this one, instead to move away; it seems that, paradoxically, the two

poles are attracted instead to be repulsed. As a matter of fact, the pole

N is repulsed

with a force

F which is composed with the weight G of the gyroscope, giving the

resultant

R, which pierces the

Ox -axis at the point Q; in conformity with the results

obtained above, the gyroscope will have a motion of precession about the

Ox -axis,

parallel to the resultant

R, coming

near to the magnet m. As we come closer to the

gyroscope with the magnet

m, as the force F grows in intensity, while the resultant R

and the

′

-axis are inclined more, the point N coming closer to the magnet. If the

pole

P is a south pole, then the gyroscope is moving away from the magnet, giving the

paradoxical impression that poles of opposite sense are repulsive.

MECHANICAL SYSTEMS, CLASSICAL MODELS

406

16 Other Considerations on the Dynamics of the Rigid Solid

Fig. 16.16 Charron’s experiment

One can establish an interesting analogy between the motion of regular precession of

the gyroscope and the uniform circular motion of a particle. Thus, to the constant

velocity

v of the particle corresponds a constant angular velocity ω of the gyroscope, to

the constant force

F which acts upon the particle corresponds the constant moment

which acts upon the gyroscope and to

⊥Fv corresponds

⊥M ω , hence the work

of the force

F vanishes ( 0⋅=Fv ), corresponding 0

⋅=M ω (the work of the mo-

ment

M is, as well, zero). The momentum vector mv, of constant magnitude, is

rotating about the fixed point with a constant velocity, while the moment of momentum

vector

′

K , constant in magnitude, rotates with a constant velocity about the fixed axis

′

. If the force F is no more acting, then mv maintains a fixed direction and the

particle has a uniform and rectilinear motion; if the moment

M does no more act,

then the vector

′

K maintains a fixed direction, while the gyroscope has a natural

regular precession about it.

16.2.1.4 The Gyroscopic Effect in Case of the Gyroscope Acted

Upon by its Own Weight

Let us consider a heavy gyroscope fixed at the point

O on its axis of symmetry (the

Lagrange-Poisson case) (Fig. 16.14). We assume that, in the initial position, determined

by Euler’s angles

00 0

,,ψθϕ,

0 θπ<<, a rapid initial rotation is imparted to the

gyroscope about its axis (

0ψθ==



, hence

0ωω==, and

constϕω== ,

the spin

ω being non-zero); the first integrals (15.2.2) lead to the relations

cosaαω θ= ,

cosbβθ= . In this case, the relations (15.2.3), (15.2.8) lead to

()

220

() 1Pu u u b u a u uω

⎡

⎤

=− −− −

⎣

⎦

(16.2.7)

ψω

−



()

uuu

ϕω ω

−

=−

−

 ,

(16.2.7')

407

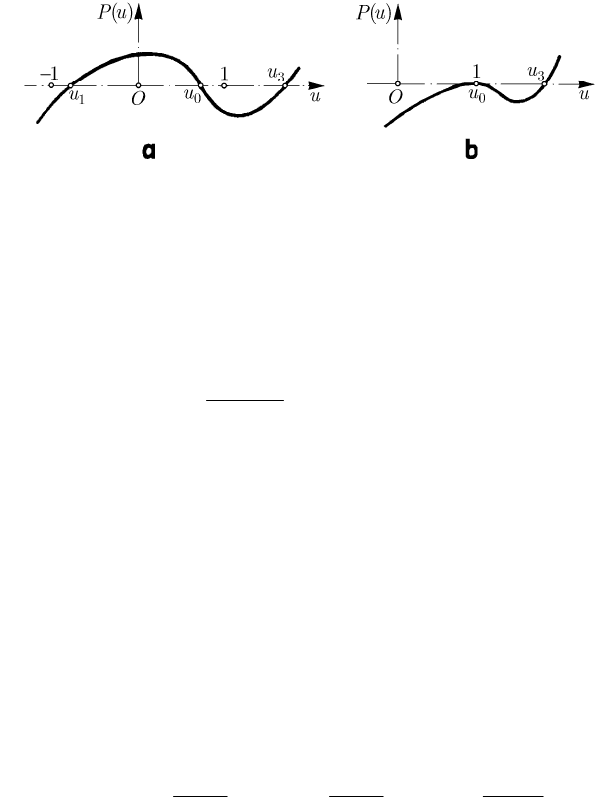
Fig. 16.17 The zeros of the polynomial ()Pu : general case (a); particular case (b)

where

cosu θ= and where we use the notations in Sect. 15.2.1.1. Following the

general theory exposed in Sects. 15.2.1.1 and 15.2.1.2, in conformity to which

102

uuu≤≤,

uuu

′

<≤, one can have only

uuu

′

==, so that

uuu≤≤

(Fig. 16.17a). Hence, the zeros

u and

u of the polynomial ()Pu will be given by the

equation of the second degree

()

uu u

a ω

−= − .

(16.2.7'')

But their calculation is not very useful, because we are interested in the behaviour of

the solution for a great spin

ω . From (16.2.7') it is seen that

sign signψω=



, so that

the

Ox -axis is rotating about the

′

-axis (motion of precession) in the same sense as

that of the initial rotation imparted to the gyroscope (about the

Ox -axis) (Fig. 16.15).

From (16.2.7") one observes that

202

0/()uubaω<−<

so that, for a great

spin

or for a very small b (hence, for a fixed point O close to the mass centre C),

the interval of variation of

u is very small; practically,

uu≅ , wherefrom

θθ≅

, the

motion of nutation being, with a good approximation, negligible. For a more exact

calculation, we put

/( )θθ εω=+ , where ()tεε= is a small parameter; it results

thus that

() () ()

00 0

222

000

333

sin

cos cos cos sin sin cos

εθ

εε

θθ θ θ

ωωω

=−≅−

which corresponds to an expansion into a Taylor series. Hence,

sin /( )uu εθω=− ,

sin /( )u εθω=−



; taking into account (16.2.7) and

neglecting the terms of higher order, the differential equation (15.2.3) with (16.2.7),

reads

()

20 2

sinbaεεω θ ε=−



(16.2.8)

Noting that

() 0tε = , we find the solution

MECHANICAL SYSTEMS, CLASSICAL MODELS

408

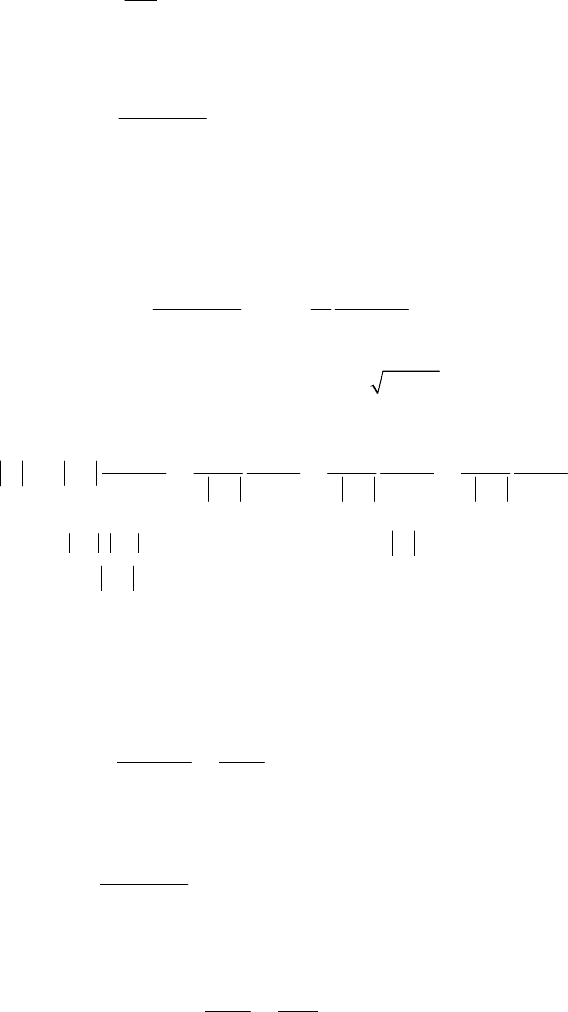
16 Other Considerations on the Dynamics of the Rigid Solid

()

[]

() sin 1 cos

tatt

εθω=−−,

(16.2.8')

wherefrom

()

[]

00 0

() sin 1 cos

tatt

θθ θ ω

=+ − −

(16.2.9)

Hence, the nutation is periodical, of period

333

2/ (/ )2/TaJIπω πω== , which

decreases at the same time with the increasing of the spin

ω (the nutation is small in

amplitude, but very rapid). The mean value of the angle of nutation will be

() ()

med

20 20

333

θθ θ

ωω

=+ =+

(16.2.9')

where we have introduced the radius of gyration

/iIM= .

From the first formula (16.2.7') it results

000

2 222

333

1 111

uu u

bbb

aaa

uuuu

ψω

ωωω

∗

−−

<< = < <

− −−−



with

max( , )uuu

∗

= ; hence, the angular velocity



is very small (of the order

of magnitude of

1/ ω or of b, if the fixed point O is very close to the centre of

gravity

C ), the motion of precession being very slow. The piercing point Q of the

-axis on the unit sphere describes a series of cycloids (we are in the case of

Fig. 15.21c). Neglecting, as above, the powers of higher order of the small parameter

ε, we find, analogously,

()

[]

1cos

sin 2

att

ψω

ωθ ω

==− −



wherefrom

()

() ()

[]

000

() sin

tattatt

ψψ ω ω

=+ −− −

(16.2.10)

The velocity of precession oscillates about the mean value

med



(16.2.10')

409

We notice also that the symmetry axis of the gyroscope does not shift in the vertical

plane (as it would be expected, due to the initial conditions and because the rigid solid

is acted upon only by its own weight – a vertical force

G), but is shifted very slowly in

a direction normal to this plane (normal to the force

G); this effect, which is in

contradictions with the direct intuition, being due to the spin

ω , is called gyroscopic

effect.

The second formula (16.2.7') allows to write

()

uuu

ϕω ω

−

<− < =

−−



bu bu

ωω

∗

−−

where

∗

has the same significance as above; hence, the angular velocity ϕ differs

very little from

ω (with a magnitude of the order of

1/ ω ), so that, from a practical

point of view, the gyroscope is rotating about its axis with the initial angular velocity.

Proceeding as above, we find

()

[

]

00 0

33 3

( /2 )cos 1 cosba a ttϕω ω θ ω=− − − ,

wherefrom

()

00 0

cos cos

() sin

tttatt

θθ

ϕϕω ω

⎛⎞

=+ − − + −

⎜⎟

⎝⎠

(16.2.11)

the mean value of the velocity of proper rotation being

med

cos

ρθ

ϕω ω

=− =−



(16.2.11')

These results are analogue to those in Sect. 16.1.2.3, corresponding to the same

mechanical phenomenon.

16.2.1.5 The Sleeping Gyroscope

In the particular case in which

0θ =

, hence

1u =

, we are led to

()()

()

220

() 1 1Pu ub uaω

⎡⎤

=− +−

⎣⎦

; the differential equation (15.2.3) reads

()()

()

11uubuaω=− +− .

(16.2.12)

The Lipschitz condition is fulfilled by the second member in the neighbourhood of

1u = ; on the basis of the theorem of existence and uniqueness, it results that the only

solution which satisfies the initial condition

1u = is () 1ut = (hence, cos 1θ = and

0θ = ). As a matter of fact, this result is illustrated in the Fig. 16.17b. The

Ox -axis of

the gyroscope remains all the time vertical, while the gyroscope “sleeps”! We obtain

MECHANICAL SYSTEMS, CLASSICAL MODELS

410

16 Other Considerations on the Dynamics of the Rigid Solid

thus a configuration called the sleeping gyroscope (the sleeping top). From (16.2.7') one

obtains

aψω=



aϕω ω=−

 ,

ψϕ ω+=



(16.2.13)

the last relation corresponding to the third kinematic equation (5.2.35) too.

Putting

1u ε=−, 1u η=− and ()tηη= being small parameters, hence giving

a small perturbation to the vertical position, we obtain

()()

()

() 2Pu b aηε η η ω ηε

⎡

⎤

=− −− −

⎣

⎦

;

neglecting the powers higher to the second one, the equation (15.2.3) reads

() () ()

222

220220202

333

22ba ba aηωηωεηωε

⎡⎤⎡⎤

=− −− −

⎣⎦⎣⎦

 .

Differentiating with respect to time and simplifying by

2η (if 0η = , then we have

constη = and we are led to a stable position of

equilibrium), we can write

() ()

20 20

2ababηω η ω ε

⎡⎤⎡⎤

+−=−

⎣⎦⎣⎦

 .

(16.2.14)

()

2abω >

, then one obtains a periodic motion of very small amplitude around

the initial position, the motion being stable; if

()

2abω ≤ , then it results an

aperiodic motion, the amplitude of which increases in time, so that the motion is labile.

Using the notations in Sect. 15.2.1.1, we can state that the motion is stable if

202

33 3

(/4 )()IJMgρω< ; hence, if the centre of gravity of the gyroscope is under the

fixed point

()

0ρ < , then the motion is stable. If the centre of gravity C is situated

over the fixed point

O (see Fig. 16.7b), then the motion of the gyroscope is stable only

if we impart to it an initial rotation

ωρ>

(16.2.15)

If, practically, we would have

() consttωω== , then the gyroscope would

continue to “sleep” for ever. But, because of the resistance of the air and of the friction

O, the velocity of proper rotation

ω decreases in time; the condition of stability

(16.2.15) does no more hold and the axis of the gyroscope is inclined more and more,

till this one falls.

16.2.1.6 The Gyroscopic Effect in Case of a Gyroscope Acted Upon

by a Concentrated Force. The Gyroscopic Moment

In the case considered in Sect. 16.2.1.4, the moment of momentum

′

is directed, at

the initial moment along the

Ox -axis of the gyroscope (Fig. 16.18a); we assume that

411

/1ωω

′

 , to can be in the case of the regular precession, so that ()

′′

=KK be at

any moment along the

-axis. The action of the own weight G leads to the moment

M applied at O, while the theorem of moment of momentum reads

′



KM; for

an interval of time

Δt we have

′

Δ=ΔKM. The extremity N of the vector

′

K will

describe a director circle of the precession cone till the point

N in the time interval Δt.

Thus, the vector

OOO

′′′

=Δ = −

JJJG



KKK will tend at the limit to d

′

being normal

to the

Ox x

′

-plane

which contains also the force G. The moment

M will be along

the same direction, the gyroscopic effect being thus put in evidence; this moment is

given by the formula (15.2.17") or, more exactly, by the formula (15.2.17'). We notice

also that, on the basis of the principle of action and reaction, the axis of the gyroscope

will exert upon the exterior with which it comes in contact a gyroscopic moment

=−MM. In this case

()

() cos

tIJI

′

⎡⎤

′

=−− ×

⎢⎥

⎣⎦

M ωω

(16.2.16)

or, with a good approximation,

()

′

=×M ωω

(16.2.16')

These two formulae are particularly useful in practice.

Fig. 16.18 The gyroscopic effect: the case

′

&K (a) and the case

′

&F (b)

Let us assume now that the moment

M is due to a concentrated force F, which acts

normal to the axis of rotation

′

, at the point Q of it; intuitively, we would expect

that, under the axis of this force, the axis does oscillate in the plane determined by its

MECHANICAL SYSTEMS, CLASSICAL MODELS

412