Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

15 Dynamics of the Rigid Solid with a Fixed Point

Multiplying the first equations (15.2.55) by

ω and

ω , respectively, we get

()

12 23

2d /dtaωω ωα+=; taking into account also the third equation (15.2.55), it

results

()

[]

()

22 22

31 2 21 2 323

ω ω ω α ω ω αωω+=− ++

Using the equations (15.1.54) and the first equation (15.2.55), we have

()

d/dtαω

()

323 1 12 21

3/4αωω ω αω αω=+−, so that

()

[]

(

)

31 2 31 211 22

ωα

ωω ω αω ωωα ωα+− =− + +

;

the first first integral (15.2.55') leads then to the fourth first integral

()

31 2 31

aCωω ω αω+− =

, constC = .

(15.2.55'')

By convenient changes of variable, the problem can be reduced to the calculation of

some hyperelliptic integrals. In 1902, R. Marcolongo showed that

ω ,

α ,

1,2, 3i =

can be expressed by means of theta functions of two arguments, each function being

linear in the time

Later, in 1946, N.I. Merkalov introduced a new variable

η, with

d/dtηω= ,

obtaining a fourth first integral in the form

() ()

22 22

12 1 12

d2d 4

ωω ω ωω η

ηη

′

+− +=− +

, constC = ,

(15.2.56)

corresponding to the case in which

′

≠

. If

′

, then we find again the

first integral (15.2.55'') (we take into account the first equation (15.2.55) and the

relation

()

12 23

2d /dtaωω ωω+=).

15.2.3.4 The Bobylev-Steklov Case

In this case, which has been – independently – put in evidence by D. Bobylev and

V.A. Steklov in 1896, one assumes that

2II= , the centre of mass being on the

Ox -axis (

0ρρ==,

0ρ > ). Euler’s system of equations becomes

()

21 2 3 23

20IIIωωω−− =



()

22 2 3 31 13

2III Mgωωωρα+− =



33 212 12

II Mgωωω ρα−=−



(15.2.57)

We obtain the particular solutions (we take into account the equations (14.1.54))

constωω== ,

kωα= ,

0ω = ,

const

==.

(15.2.57')

373

MECHANICAL SYSTEMS, CLASSICAL MODELS

In this case, the equations (14.1.54) take the form

123

kααα=−



213

αωα=



()

3211

kαααω=−



(15.2.58)

We get the first integral

11 2

2 kCωα α+=

, constC = ,

(15.2.58')

using the first two above equations. Taking into account also (15.1.44), we can write

()

22 2

32 2

1ααλμα=− − − ,

and, replacing in the second equation (15.2.58), we are led to the elliptic integral

()

02 2

ωξλμξ

−−−

∫

(15.2.58'')

the problem being thus completely solved.

15.2.3.5 Other cases of integrability of Goryachev, Steklov and Chaplygin

At the beginning of XXth century, Goryachev, Steklov and Chaplygin have put the

problem to find new cases of integrability, where the first integrals, independent of

time, be algebraical, not containing arbitrary constants. Thus, assuming that

0ρρ==, Chaplygin searched the conditions in which there exist integrals of the

form

12 12 1 2

ρα δωω λω ω−= + ,

13 13 1 3

ρα εωω μω ω−= +

(15.2.59)

for the equations of Euler and Poisson; the constants

δ, ε, λ and μ remain to be

determined.

Goryachev considered in 1898 the case in which

0λ = and 3n = . Assuming that

()()

13 1 2 2 3

82II I I I I=− −, he put into evidence the existence of the integrals

(15.2.59), with

−

=−

()( )

23 2 3

22 2 3II I I

−−

=−

()()

()

12 3 2 3

123 2 3

4345

II I I I

II I I

δε

−−

−

(15.2.60)

which contain only one arbitrary parameter.

In 1899, Steklov studied the case in which

0λμ==, finding

()()()()

31 21 3121

22II II IIIIδε−=−=− −,

(15.2.61)

374

15 Dynamics of the Rigid Solid with a Fixed Point

in the hypothesis in which

21 3

2II I>> . The components

123

,,ωωω of the vector ω

are, in this case, in direct proportion to

cn tκ , sn tκ and dn tκ , respectively, where κ

depends on

123

,,III and

ρ .

Chaplygin assumed in 1904 that

1/3n =− and that the relation

()()

1213 23

92 24IIII II−−= takes place, with

0.5965 / 0.6000II<<,

1.5000 / 1.5965II<<. He showed that the integrals (15.2.59) exist for

()()()()

31 21 2131

22II II IIIIδε−=−=− −,

()

31 2

II I

−

()

21 3

II I

−

(15.2.62)

where

s verifies the equation

()

[]

()()

21 31

33 2

1231 1

1213

42 2

93232

II II

IIIIs

IIII

−−

+− =

−−

(15.2.62')

By a transformation of Hermite type, the solution of the problem can be represented

with the aid of the elliptic integrals.

Chaplygin showed also that these are the only cases in which one can find integrals

of the form (15.2.59).

15.2.3.6 Other Particular Cases of Integrability

N. Kovalevski considered in 1908 the case in which the mass centre is on the principal

axis

Ox (

0ρρ==), searching all the cases in which

ω and

ω can be expressed

in the form of polynomials of the third degree in

ω . Thus, he found again the

particular cases studied by Goryachev, Steklov and Chaplygin (see Sect. 15.2.3.5), as

well as a new case in which the relation

()()

12 3 223

910 18II I III−= − takes

place. Much later, in 1932–1934, J.J. Corliss assumes also that

0ρρ==, but

imposes the condition

′

too, limiting thus the generality of the initial

conditions. A particular case of the above one has been considered by P. Field in the

same period of time. He deals also with the interesting case in which

I is close to

I ,

while

I is small, so that the ratio

()

123

/III− be practically indeterminate.

P.V. Myasnikov proposed in 1954 a new method to find cases of integrability in a

unitary mode, assuming that the centre of mass

C lies in the characteristic plane,

determined by the vectors

ω and

′

K ; in this case, one obtains a fourth first integral of

the form

11 1 22 2 33 3

constII Iρω ρω ρω++=

. (15.2.63)

If the point

C is situated at the same time in the characteristic plane and on one of the

principal axes of inertia at

O, one obtains again various classical cases previously

considered (Euler-Poinsot, Lagrange-Poisson, Bobylev-Steklov etc.).

375

MECHANICAL SYSTEMS, CLASSICAL MODELS

In 1950, T. Manacorda and A. Nadile have considered the planar case of motion of a

rigid solid with a fixed point (after P. Stäckel’s terminology), hence the case in which

the mass centre is situated in one of the principal planes of inertia; there have been thus

put in evidence various relations which take place, as well as the cases of integrability

which can be obtained.

In 1959, E.I. Harlamova formed a new case of integrability of the equations of Euler

and Poisson, assuming that

0ρ = ,

0ρ < ,

()()()()()()

131 132 31 33 1 3123 1

22220II III II I I IIII Iρρ−−−+− −−=

and

312

22III>>; but the last hypothesis is not possible from a physical point of

view. M.P. Gulyev showed in 1961 that this solution is however possible in the case of

a body filled up with an incompressible perfect fluid. This is the only case of regular

precession with respect to a vertical line, dynamically possible.

The possibility to find linear integrals has been investigated by P.V. Harlamov in

1962, being stimulated by Chaplygin’s affirmation in conformity to which linear

integrals other than those known at the respective moment do not exist, but which was

afterwards contradicted by the discovery of such integrals.

A.N. Filatov introduced in 1963 the notion of generalized Lie series, which allowed

the systematic determination of a fourth first integral in various known cases of

integrability.

15.2.3.7 Permanent Axes of Rotation

In 1894, O. Stande and B.K. Mlodzeevski have shown – independently – that the

equations of Euler and Poisson allow a simple infinity of solutions if no one restriction

concerning the rotations of the rigid solid about fixed axes in the solid and in the space

is imposed. Mlodzeevski showed that such permanent axes of rotation can be the

principal axes of inertia, if these axes are horizontal (the case of the physical pendulum)

or a family of vertical axes; in the latter case, studied in detail by Stande, the magnitude

of the instantaneous angular velocity is constant.

In this order of ideas, we search a constant unit vector

′

i satisfying these equations.

We notice that Poisson’s equation is reduced to

′

×=

i0ω (because

′



i0; hence,

′

=± iω ,

(15.2.64)

so that

ω is a constant vector too. The equation (15.1.21'') becomes

()

33 3

Mgω

′′ ′

×=×iIi i

(15.2.65)

Hence, if the constant unit vector

′

i and the constant scalar ω satisfy the equation

(15.2.65) and the equation

′

=i , then

const

′





i and (15.2.64) represents a

solution of the equations of Euler and Poisson. If – in the above conditions – a rigid

solid with a fixed point

O begins to move with an angular velocity of rotation ω about

an axis rigidly linked to the rigid solid, specified by the unit vector

′

i and if this axis is

situated along the ascendent vertical, then the rigid solid remains in a state of

376

15 Dynamics of the Rigid Solid with a Fixed Point

permanent rotation about the respective axis. A scalar product of the equation (15.2.65)

′

Ii allows to write

()

,, 0

′′

Ii i

(15.2.66)

or, in a scalar form

() () ()

11 22 33

123

2 3 123 3 1 231 1 2 312

III

II II II

ααα

ρρρ

ραα ραα ραα=− +− +− =

(15.2.66')

this is the condition which must be verified by the unit vector

′

i , hence by the direction

cosines

α ,

1,2, 3i =

. We can thus state that the permanent axis of rotation must be on

the cone of the mass centres relative to the fixed point

O, of equation

() () ()

11 22 33

123 231233123112312

123

Ix Ix Ix

xxx IIxxIIxxIIxxρρρ

ρρρ

=− +− +− =.

(15.2.66'')

This cone is concentric with the ellipsoid of inertia at

O, but is not coaxial with this

one. If we take an element of the cone, to which we impose a certain sense, then we

obtain the direction cosines

α , 1, 2, 3i = , while the formula (15.2.65) allows to

calculate the quantity

ω; we notice that the signs must be chosen (we can have

α± ) so

that the quantity

ω be positive. We still observe that the moment of momentum is

situated along the axis of direction parameters

I α ,

I α , called secondary axis

too; hence, the centre of mass lies on a plane determined by the axis of rotation and by

the secondary one. It can be easily seen that the three principal axes of inertia, the

OC-axis and the OC

′

-axis, where C

′

is a centre associated to the mass centre, of co-

ordinates in direct proportion to

/Iρ ,

/Iρ , are five exceptional axes

situated on the cone of the mass centres. The intersection of this cone with the unit

sphere of centre

O is called the mass centre curve and plays an important rôle in the

study of the motion too; considering that

α ,

1,2, 3i =

, are the co-ordinates of a point

on the sphere, it results that the equations (15.2.66), (15.2.66') are just the equations of

this curve.

In the case of an ellipsoid of inertia of rotation (

123

III=> or

123

III>=) one

obtains interesting particular results, after the position of the mass centre. If

= 0

then we are in the Euler-Poinsot case, the corresponding problem being studied in Sect.

15.1.2.7.

377

MECHANICAL SYSTEMS, CLASSICAL MODELS

15.2.3.8 Other Cases of Loading. The Nadolschi Case

Euler considered in 1758 the most simple case of loading of the rigid solid with a fixed

point, i.e. the case in which the resultant moment of the given forces vanishes

(

=M0). Another case, particular too, is that in which the direction of the moment

M is rigidly connected to the rigid solid ( ()

Mt=Mu, const=





u in the frame

of reference

R ), but is movable with respect to the fixed frame

′

R . R. Grammel calls

autoexcited rigid solid that solid which is acted upon by a moment

()

tM resulting

from internal actions of the respective solid, which does not change in an appreciable

manner the distribution of masses. One can consider also the case in which the vector

function

()t=uu is given. Firstly was studied the simpler case in which const

M =

(stationary autoexcitation) and then the case

()

MMt= (non-stationary

autoexcitation). One obtains different results, as the moment

M is situated along the

minor axis, the major axis or the mean axis of the ellipsoid of inertia. We mention also

that in the phase space one obtains diagrams of the type of those in Figs 7.22 and 7.25.

In 1952, U.T. Bödewadt considers the case of a symmetric ellipsoid of inertia

(

II= ), the rigid solid being stationary autoexcited, with const=





u ; realizing a

partial decoupling of Euler’s equations, he could give a solution by means of some

Fresnel’s integrals. W. Braunbeck studied in 1953 the case of a symmetric rigid solid

hanged up at its mass centre

C and acted upon by a moment of the form (external

excitation)

()

[

]

()t μ=×−MuHH,

(15.2.67)

generated by a bar of magnetic moment

μ, situated along the symmetry axis and

subjected to the action of a homogeneous magnetic field

=+HH H, where

H is a

constant field, while

H is a field which varies periodically with t; the unit vector u is

situated along the axis of symmetry. If

=HH (

=H0), then the motion of the rigid

solid is identical to that due to the influence of a gravitational field. Interesting results

have been obtained for

HH or

⊥HH.

The case of gravity forces, which has been studied at large, is a conservative case.

We will consider also the case of arbitrary conservative forces, of potential

()

123

,,UU

′′′

= iii , where

′

, 1, 2, 3j = , are the unit vectors of the fixed frame of

reference

′

R ; we assume the presence of a gyrostatic moment

m (of the nature of a

moment of momentum) and of some intrinsic cyclic motions (due, e.g., to symmetric

rotors or to voids completely filled with an incompressible ideal fluid) too. The

equations of Euler and Poisson are then of the form

()

′

+× =−× − ×∇



II miωω ω ω

, constL = ,

(15.2.68)

′′

+× =



ii0

1, 2, 3j =

(15.2.68')

Excepting the obvious six first integrals

378

15 Dynamics of the Rigid Solid with a Fixed Point

kjk

′′

⋅=ii ,

,1,2,3jk=

(15.2.69)

we mention the first integral of the mechanical energy

()

Uh⋅=+I ωω , consth = .

(15.2.69')

The problem has been dealt with in detail, in 1986, by H.M. Yehia, in the case in which

the conservative and the gyroscopic forces allow a common axis of symmetry, which

passes through the fixed point

O. In the symmetric case, F. Brun, in 1907, O.I.

Bogoyavlenski, in 1984, and H.M. Yehia, in 1986, have put in evidence six cases of

integrability. Thus, if

12 3

2II I== ,

303

I ω=mi,

constω = ,

′

=⋅i

1, 2, 3j = , being constant vectors in the plane

Ox x

; the dimensions of all these

quantities are chosen so as to verify the dimensional equations (

ω is an angular

velocity and

is an angular acceleration). We find the first integral

()

[

]

12 11 22 12 12 21

jj jj jj jj

ii iiωωγ γ ωω γ γ

′′ ′′

−− + + − +

()

03 0 1 2 011 223

24const

jjj

iωω ω ω ω ωωγ ωγ

′

+− +− + =

(15.2.70)

where

γ ,

′

, ,1,2,3jk= , are the components of the vectors

and

′

i ,

respectively, along the

Ox -axis. By particularization, one obtains various interesting

results, among them the first integral of Sonya Kovalevsky.

In 1944, V.L. Nadolschi studied the case in which the ellipsoid of inertia is

symmetric (

IIJ==), the moment of the given forces being of the form

()

t=MM. Euler’s equations are of the form

()

ωω−=



()

ωω+=



()

ω =



(15.2.71)

where

()

() / ()

tJ JI tω=− . Eliminating successively

ω and

ω ,

respectively, we find the equations

1111

() () ()

tft tωωωΦ++=



 

{

}

()

() () () ()

tMtMtft

Φ =+

⎡

⎤

⎣

⎦

2222

() () ()

tft tωωωΦ++=



 

{

}

()

() () () ()

tMtMtft

Φ =+

⎡

⎤

⎣

⎦

(15.2.72)

379

MECHANICAL SYSTEMS, CLASSICAL MODELS

The third component of the angular velocity is given by (

()

330

tωω= )

()

() d

tMtt

ωω=+

∫

(15.2.72')

By a change of independent variable

()

ττ ω

−

=−

∫

(15.2.73)

we get

d()

() ()

ωτ

ωτ Φτ

d()

() ()

ωτ

ωτ Φτ

wherefrom (we use the method of variation of constants)

11 12

() ()sin( )d cos sinuuuCC

ωτ Φ τ τ τ=−++

∫

22 12

( ) ( )sin( )d sin cosuuuCC

ωτ Φ τ τ τ=−+−

∫

(15.2.74)

We notice also that, using only the function

()Φτ, we obtain

()

21 12

()

( ) ( )cos( )d sin cos

()

uuuCC

ωτ Φ τ τ τ

ωτ

=− − + − −

−

∫

(15.2.74')

C and

C being, as above, integration constants. Euler’s angles are then obtained by

quadratures.

380

Chapter 16

Other Considerations on the Dynamics of the Rigid Solid

The modelling of a continuum as a rigid solid allows the study of many problems of

practical interest. In this order of ideas, we consider, in the frame of this chapter, the

motions of the Earth and make a presentation of the theory of the gyroscope; as well,

we deal with the model of the rigid solid of variable mass, with applications to the

motion of the aircraft.

16.1 Motions of the Earth

The theory developed in the previous chapters concerning the dynamics of the rigid

solid may be applied successfully to the study of the motion of the Earth with respect to

a heliocentric frame of reference

′

, considered to be inertial (fixed) and with respect

to a geocentric non-inertial (movable) frame

R. Modelling the Earth as a rigid solid,

one can put in evidence the motion of revolution about the Sun, the motion of rotation

about its axis, as well as the motions of precession and nutation. We mention other

motions of the Earth too, as: the displacement of the geographic poles of the Earth on

its surface, the tides (studied in Chap. 10, Sect. 2.2.3), the displacement (drift) of the

continents etc.

16.1.1 Euler’s Cycle. The Regular Precession

In what follows, we give firstly some general results concerning Euler’s cycle, passing

then to the calculation of the regular precession; we put thus in evidence the

corresponding secular variations. By analogy, we consider then the Larmor precession.

16.1.1.1 General Considerations

In a modelling as a particle, the Earth is attracted by the Sun (modelled as a particle

too), considered to be fixed, after the law of universal attraction, having a Keplerian

motion with respect to the latter one; as a matter of fact, this is the motion of the mass

centre C of the Earth, if we assume that the forces of attraction which act upon it have a

resultant passing through this point. In reality, the Earth is not a homogeneous sphere or

is not formed by homogeneous spherical strata, the above condition concerning the

resultant of the attraction forces being fulfilled only approximately (see Chap. 9, Sect.

1.2 too); hence, the trajectory of the point C differs from an ellipse, this one being only

a first approximation of the real one. However, we will assume that the mass centre C

describes an ellipse, the Sun being situated at one of the foci, as it was shown in Chap. 9,

P.P. Teodorescu, Mechanical Systems, Classical Models,

381

MECHANICAL SYSTEMS, CLASSICAL MODELS

Sect. 2.1.4; this approximation is as more acceptable as the perturbations due to the

presence of other celestial bodies are less important. The respective motion of

translation is called motion of revolution about the Sun during a sidereal year; it has

been put in evidence by considerations concerning the aberration of light and the stellar

parallax.

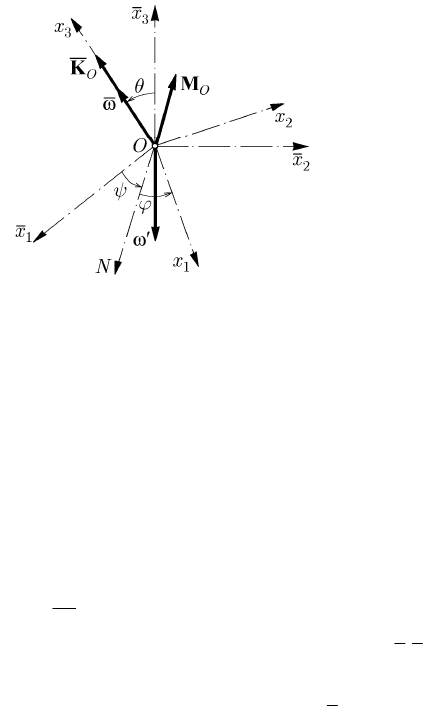
Fig. 16.1 Non-inertial frames of reference in case of the motions of the Earth

The motion of rotation of the Earth about the centre C is independent on its motion

of revolution about the Sun, mentioned above. To study this motion, we will consider a

non-inertial (movable) frame of reference

R, rigidly linked to the Earth and having the

pole at its centre (

OC≡ ); the central principal axes of inertia of the Earth will be

taken as axes of the frame

R. We will assume, in a first approximation, that the Earth is

an oblate spheroid (ellipsoid of rotation with respect to the minor axis), choosing the

axis of the poles as

Ox -axis (directed towards the north pole, putting thus in evidence

the sense of the diurnal motion of the Earth); the plane

Ox x will be the equatorial

plane of the Earth and it results

312

IIIJ>== (the hypothesis thus made is

acceptable, because

()

123

/10/3III

−

−<). It is convenient to introduce also a

geocentric frame of reference

R with the axes parallel to the axes of the heliocentric

frame

′

and with the pole at the same pole O. We choose as plane

Ox x

the plane

of the ecliptic (which contains the trajectory of the pole

O), the heliocentric frame

being, as well, an ecliptic heliocentric frame; the sense of the

-axis will be chosen

so that the motion of the mass centre on its trajectory have a positive sense with respect

to this axis. The line of nodes

ON will be at the intersection of the ecliptic plane with

the equatorial plane of the Earth, being directed towards the first point of Aries, which

indicates the vernal equinox (Fig. 16.1).

16.1.1.2 Diurnal Rotation of the Earth. Euler’s Cycle

By means of the usual notions in the dynamics of the rigid solid, we can write Euler’s

equations (15.1.11") in the form,

382