Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

15 Dynamics of the Rigid Solid with a Fixed Point

We present firstly a general study of the motion, determining the rotation angular

velocity vector and putting stress on the motion of precession; we pass then to a

geometric representation of the motion, using the results obtained by Poinsot in this

direction.

15.2.1.1 Integration of the Equations of Motion

The motion of the heavy rigid solid with a fixed point is governed by Euler’s equations

(15.1.21); these equations take the form

()

13 23 32

JIJ Mgωωωρα+− =



()

233131

JJI Mgωωωρα+− =−



0ω =



(15.2.1)

in the Lagrange-Poisson case. We obtain

()tωω= ,

(15.2.1')

the constant

ω being called spin, while the first integrals (15.1.42'), (15.1.43') take the

form

()

11 22 33 3

JIKωα ωα ω α

′

++ =

()()

22 0

12 33 33

22JIMghωω ω ρα++ =− +.

(15.2.1'')

The first integrals (15.2.1'), (15.2.1''), together with the first integral (15.1.44), form the

system of four first integrals necessary in the general theory to solve the problem.

Unlike the Euler-Poinsot case, the kinetic and the kinematic aspects cannot be

separated in this case. It is convenient to replace the direction cosines

123

,,ααα of the

′

-axis with respect to the frame of reference R by the relations (5.2.36); it results

()

12 33

sin cos sin cos

JIKωϕω ϕθ ω θ

′

++=

()()

22 0

12 33 3

2cos2JIMghωω ω ρ θ++ =− +.

(15.2.1''')

Associating the relations (5.2.35) and eliminating the components

ω and

ω , we get

the system of equations

sin cosaψθαω θ=−



sin cosbψθθβ θ+=−



cosψθϕω+=



(15.2.2)

where we have introduced the notations

KJα

′

()

2/hI Jβω

⎡

⎤

=−

⎣

⎦

/0aIJ=>,

2/0bMgJρ=>; we notice that α and β are constants which

depend on the initial conditions, while the constants

a and b are functions only of the

geometry and the mechanical properties of the rigid solid.

343

MECHANICAL SYSTEMS, CLASSICAL MODELS

The system of differential equations (15.2.2) will determine Euler’s angles

()tψψ= , ()tθθ= and ()tϕϕ= . Eliminating ψ



between the first two relations,

we obtain

()

0222

cos ( cos )sin sinabαω θ β θ θθ θ−=− −



Denoting

cosu θ= , it results the differential equation

()uPu=



()

()( )

() 1Pu bu u a uβαω=− − −−

(15.2.3)

wherefrom

()

∫

(15.2.3')

with

cosu θ= ,

()

tθθ= ; the radical is taken with the same sign as

()



assuming that

()

0ut ≠



, ( ()ut



has a continuous variation, beginning from

()



Fig. 15.19 The graphic ()Pu vs u. The cases

uu≠ (a) and

uuu== (b)

0θ ≠ and

θπ≠ , then we have

()

1,1u ∈− ; we notice that ()0P −∞ < ,

() 0P ∞> and (1) 0P ±<, in the hypothesis in which

aαω≠± , hence

KIω

′

≠±

. Because the equation (15.2.3) allows a solution only if

()

0Pu ≥ , it

results that the polynomial

()Pu is of the form

12 3

() ( )( )( )Pu bu u u u u u=− − −,

(15.2.3'')

where

123

,,uuu are the real zeros of the polynomial of the third degree ()Pu , so that

102 3

11uuu u−< ≤ ≤ < < <∞; the graphic of this polynomial is given in

Fig. 15.19a (to draw this graphic, we assume that

/2θπ≤ , hence

0u > ) for

uu≠

and in Fig. 15.19b for

120

uuu==. Because

uu≤ , it results that

θθ≥

(we have

0 θπ≤≤), so that the nutation

[

]

,θθθ∈ . We notice that the integral

(15.2.3), (15.2.3') is of the form (7.1.4) to (7.1.5); following the same reasoning as in

344

15 Dynamics of the Rigid Solid with a Fixed Point

Chap. 7, Sect. 1.1.1, we can state that

()ut varies periodically between

u and

u , the

duration of a complete period being

()

∫

(15.2.3''')

Hence,

()()ut T ut+= and ()()ut T ut+=



; it results, as well ()()tT tθθ+= .

By the change of variable

/uvcc

′

, where

/4cb=

and

()

/3ca bβω

⎡⎤

′

⎣⎦

, we can replace the polynomial ()Pu by a polynomial of

the form

() 4Qv v gv g=−−,

,constgg= ; the relation (15.2.3') becomes

()

ct t

−=

∫

(15.2.4)

where

()

vcuc

′

=−

. Denoting

()

;,vggα= P , we introduce the variable α

through the agency of the elliptic function

P of Weierstrass, corresponding to the

constants

g and

g ; this function verifies the differential equation

d()

4() ()

αα

⎡⎤

=−−

⎢⎥

⎣⎦

so that

()

ct tαα−= −, where

α is given by

()

0023

;,vggα= P . The function

()ut (and, implicitly, the angle of nutation ()tθ ) will be given by

()()

() cos ()

ut t c c t t

θα

′

==+ −+P .

(15.2.4')

We can introduce a new variable

κ by the relation

()

22 2

12121

cos sin sinuu u u u uκκ κ=+=+−

()

221

cosuuu κ=− −

()

331

1sinuuu k κ=− − −

−

(15.2.5)

Replacing in (15.2.3'), (15.2.3''), we get

()

1sin

pt t

−=

−

∫

()

bu u

−

(15.2.6)

345

MECHANICAL SYSTEMS, CLASSICAL MODELS

where

κκ= corresponds to

uu= . Denoting sinw κ= , we can write

()

()( )

pt t

ζζ

−=

−−

∫

(15.2.6')

too, with

sinw κ= . By means of the elliptic integral of the first kind

()

,Fkκ ,

given by (7.1.41), one can use also the formula (15.1.51'). Introducing Jacobi’s elliptic

functions, it results, as well,

() () ( )()

22 2

102 0121 0

( ) cn sn snut u ptt u ptt u u u ptt=−+ −=+− −

()()()()

221 0 331 0

cn dnuuu ptt uuu ptt=− − − =− − − . (15.2.5')

Taking into account the relation (

123

,,eee are the zeros of the polynomial ()Qv )

()

sn ;

−

⎛⎞

⎜⎟

−

⎝⎠

P ,

(15.2.7)

which links the elliptic function of Weierstrass to the Jacobi elliptic functions, we can

pass from the formula (15.2.4') to the formulae (15.2.5'). The period (15.2.3''') can be

expressed by a formula of the form (15.1.54). The motion of nutation is thus put in

evidence. We can set up two circular cones of common axis

′

and angles at the

vertex

2θ and

2θ , respectively; the

Ox -axis describes a cone contained between

these two cones (Fig. 15.20a). If the two mentioned cones form only one cone

(

() 0Pu = has a double root, hence

θθ= ), then this cone will be a circular one. The

other angles of Euler will be given by the equations (15.2.2), in the form

αω

−



()

auu

αω

ϕω

−

=−

−



(15.2.8)

It results that ()()tT tψψ+=



and ()()tT tϕϕ+=



, so that

()()tT tψψΨ+= +,

()()tT tϕϕΦ+= +,

(15.2.8')

where

Ψ and

Φ are constant in time.

Research in this direction has been made by C.G.J. Jacobi, E. Lottner, O.I. Somov,

C. Frenzel, A. Söderblom, J. Chrapan etc.

15.2.1.2 Motion of Precession. Regular Precession

As in Sect. 15.1.2.2, to can appreciate easier the motion of the rigid solid and to can

make easier the determination of its position, we will consider the motion on the unit

sphere of centre

O of the point Q at which the movable

Ox -axis pierces it

(Fig.15.20a); the position of the point

Q will be specified by the colatitude θ and by the

346

15 Dynamics of the Rigid Solid with a Fixed Point

longitude

/2ψπ− . The point Q will describe on the sphere a curve Γ of equation

()

ψψθ=

, contained between the parallels

θθ= and

θθ= ; taking into account

(A.1.41') and adapting the notations, the element of arc on the curve will be given by

the relation

222222

ddsind ddsss

θθψ=+ =+ (Fig. 15.20b). The angle V made by

the curve

Γ with a meridian circle at the point Q is given by tanV

d/d sind/dss

θψ θ== . Due to

cosu θ=

, we have d/d sind/duψθ θψ=−

sin d /dtuψθ=−



; taking into account (15.2.3), (15.2.8), we may write

Fig. 15.20 Motion of precession on the unit sphere (a). The curve Γ on a spheric zone (b)

()

tan

1()

uPu

αω−

−

(15.2.9)

where we have no more mentioned the sign before the radical. Let us denote by

333

//1

uaKIαω ω

′

′′

== ≠±

(corresponding to the previous hypothesis) the

value of

u which equates to zero tanV ; from (15.2.8) it results that ψ



vanishes for

′

= too. If

[]

,uuu

′

∈ 

, hence if u

′

is not a possible value for u, then ψ



has

always the same sign (it never vanishes), while

ψ varies in the same sense (increasing

or decreasing); the meridian plane is rotating in the same sense and the point

describes the curve

Γ (Fig.15.21a). We notice that for

uu= and

uu= we have

/2V π= , the curve being tangent to the parallels

θθ= and

θθ= . If

()

,uuu

′

∈ , then ψ



changes of sign when u passes through the value u

′

; the angle

of precession varies in both senses, while the curve forms loops, being tangent to the

parallels

θθ=

and

θθ=

(because /2V π= ) and normal to the parallel θθ

′

(which corresponds to

′

= ), because

tan 0V =

. Obviously, the double points are

347

MECHANICAL SYSTEMS, CLASSICAL MODELS

on the same parallel and on the meridians which pass through the points of tangency of

the curve

Γ with the parallel uu

′

= (Fig. 15.21b). It remains to consider the case in

which

′

= or

′

= ; in this case

()

0Pu

′

= , while from (15.2.3) it results

/ubβ

′

= . We calculate the derivative ()Pu

′

starting from the relation (15.2.3) or

from the relation (15.2.3''); in the first case,

()

10Pu b u

′

=− − <

and

()

10Pu b u

′

=− − < , while in the second case we have

() ( )( )

12131

0Pu bu u u u

′

=− −> and

() ( )( )

22132

0Pu bu u u u

′

=− − − < .

Hence, we cannot have

′

= , but only

′

= . The corresponding curve Γ is

tangent to the parallel

θθ=

. We notice that the difference

auαω− is of the order

of magnitude of

uu− , while

()Pu

is of the order of magnitude of

uu− , so

that

tan 0V → for

uu→ , the curve Γ being tangent to the meridian circle on the

parallel

θθ= . On the other hand, from (15.1.95) it results that

()

sign sign auψαω=−



()

sign 1uu=−= for

uu< , while

()

0uψ =



;

hence, the angle

ψ is constantly increasing, the points at which the curve Γ reaches the

parallel

θθ= being cuspidal points (Fig. 15.21c).

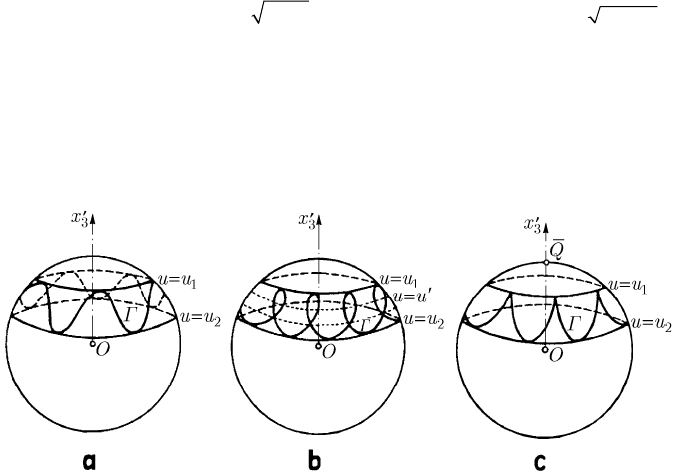
Fig. 15.21 The drawing of the curve Γ on a zone of the unit sphere. The cases

[]

,uuu

′

∈ 

(a),

(, )uuu

′

∈

(b) and

′

= or

′

= (c)

In conclusion, the point

Q (hence the axis

Ox too) has a motion of nutation and a

motion of precession between the two parallels

θθ= and

θθ= , with the velocity

sinθψθ

′



vn i

2222

sinv θψ θ=+



. Taking into account (15.2.8'), we can show

that the curve

Γ is, in general, an open curve, excepting the case in which

commensurable with

π.

It remains to consider also the case in which

333

//1

uaKIαω ω

′

′′

== =

. From

(15.2.3) we notice that we can write

348

15 Dynamics of the Rigid Solid with a Fixed Point

2202 2

() ( )(1 ) ( )( )Pu bu u a u uβω

′

=− − − −.

Hence, if

′

= , then we have

()

10P = , so that

cos 1u θ== and

0θ = , while

the superior parallel

uu= is reduced to the piercing point Q of the

′

-axis on the

unit sphere; the curve

Γ has the form drawn in Fig. 15.21c, the point Q being a

multiple cuspidal point. Such a situation takes place, for instance, if the

Ox -axis

coincides with the

′

-axis at the initial moment (hence

0θ = ). We cannot have

′

=− because, in this case, we would have

1u =− too, hence

′

= , which we

have seen that it is not possible.

The first formula (15.1.95) can be written also in the form

33 33

()

uu uu u

ωω

′′

−−

wherefrom

()()()

33 1 2 3

Jb u u u

Iuuuuuuu

′

−

−−−−

∫

(15.2.10)

Ψψ ψ=− representing the variation of the precession in the semi-period T/2.

Projecting the curve

Γ on the equatorial plane (normal to the

′

-axis), one obtains a

curve contained in a circular annulus and successively tangent to the limit circles; the

angle at the centre in this plane, formed by two successive points of tangency, is the

apsidal angle

Ψ (the angle formed by two meridian planes which pass through two

successive points of tangency to the parallels

uu= and

uu= ). If the above integral

has a positive value (e.g., if

′

≥ ), then

()

21 3

sign signψψ ω−=

, while if the

integral has a negative value (e.g., if

′

< ), then the precession verifies the relation

()

21 3

sign signψψ ω−=− . Following a demonstration given by J.B. Diaz and F.T.

Metcalf in 1962, if

()

,uuu

′

∈ , then we can write

()()() ()()()

2 2

1 1

12 3 12 3

1d 1d

uu uu

uu u uu u uu u uu u

′′

+−

=−

−−− −−−

∫∫

()()()

()()

()

()()

123 12

11d

111 1

uuu

uuu uuuuu

′

+++ + − −

∫

()()()

()()

()

()()

123 12

11d

11 11

uuu

uuu uuuuu

′

−−

−

−− − − − −

∫

where we have used the inequalities

33 3

11uuuu−< − < +. But from

(15.1.90'') one observes that

349

MECHANICAL SYSTEMS, CLASSICAL MODELS

()()()

()

()()

()

020

123

111

aa u

uuu

bb b

αω ω

′

−

+++=− = =

;

analogously,

()()()

()

()()

()

020

123

11 1

aa u

uuu

bb b

αω ω

′

−−

−− −=−= =

It results thus

()()

()

()()

()( )( )

12 12

312112

11d 11d

uuu uuu

uuuuu u uuuu

++ −−

⎡⎤

>−

⎢⎥

+−− − − −

⎣⎦

∫∫

By the substitution

uv=− we notice that the second integral in the parenthesis is

equal to the first one. Moreover, by the substitution

()

1/ 1vu=+ we have

()

()()

()()( )

12 12

11 2 1

uuuuu

uuv uuv

=−

+−−

−+ + + + + −

∫∫

()()

12 1 2

2211

arc sin

uu u uv

++− + +

−

so that the two above equal integrals equate

π; as a consequence, 0J > . We find thus

again a proposition obtained in 1895 by J. Hadamard (corresponding to an affirmation

of Halphen, based on fastidious demonstrations), by using the method of residues of the

functions of complex variables; we can state

Theorem 15.2.1 (Halphen-Hadamard) The apsidal angle Ψ has the same sign as the

spin

ω (

sign signΨω= ) if

′

> and an opposite sign (

sign signΨω=− ) if

′

< .

We can show also that the sign of

Ψ is the same as the sign of dψ for

uu= (the

lowest position of the point

Q on the curve Γ).

Other researches in this direction have been made by A. Métral. Superior and

inferior limits for the apsidal angle

Ψ have been put in evidence by W. Kohn in 1946,

being found again – using simpler methods – by Diaz and Metcalf in 1964.

Analogously, the second formula (15.2.8) allows to calculate the variation of the

angle of proper rotation in the form (

Φϕ ϕ=−)

()

()()()

3123

uuu

uuuuuuu

′

−

⎡⎤

=−

⎢⎥

−−−−

⎣⎦

∫

(15.2.10')

We assumed above that

uu< ; in the case of a double root (

120

uuu==,

Fig. 15.19b) we have

()ut u= , hence

()tθθ= . From the relations (15.2.8) it results

350

15 Dynamics of the Rigid Solid with a Fixed Point

that ψ



and ϕ



are constant. Hence, the

Ox -axis (rigidly linked to the rigid solid)

describes a circular cone around the

′

-axis, called cone of precession, with a

constant angular velocity



(of precession), while the rigid solid is uniformly rotating

(with the velocity of proper rotation



) about the

Ox -axis. This is the case of a

regular precession (a uniform motion of precession). The double root

u must verify

the relations

()

0Pu = and

()

0Pu

′

= ; eliminating the differences

buβ − and

auαω− and taking into account the relations (15.2.8) written for the initial moment

(

()

tψψ=



and

()

tϕϕ=



), we get the equivalent conditions

()

02 2

330 0 300 3 0 0 3

cos cosIJ I JI Mgωψ ψθϕψ ψθ ρ−=−− =

  



(15.2.11)

which must be verified by the initial conditions in the case of the regular precession. If,

in the Euler-Poinsot case, the ellipsoid of inertia would be of rotation, then the motion

of precession would be always regular; but, in the Lagrange-Poisson case (the ellipsoid

of inertia being always of rotation), the regular precession takes place only for

particular initial conditions. If the conditions (15.2.11) are only approximately verified

(e.g., in the motion of the Earth, when the angle

θ is no more constant), then the motion

is called pseudoregular precession.

As a matter of fact, we must mention that also other motions for which the imposed

integrability conditions are only approximately verified have been considered. Thus, A.

Pignedoli studied a pseudocase Lagrange-Poisson, in which the mass centre

C is no