Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

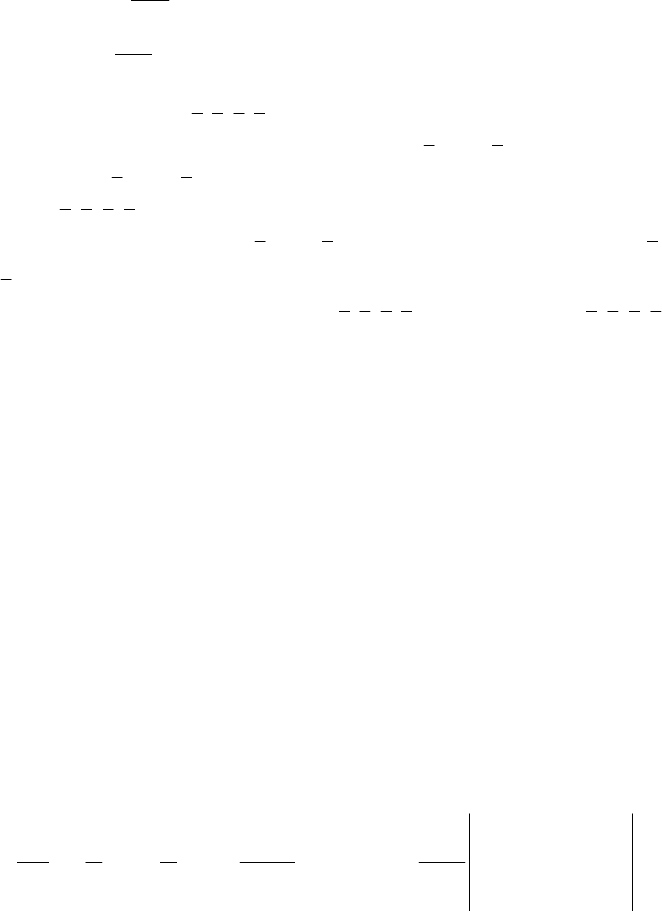
15 Dynamics of the Rigid Solid with a Fixed Point

()()()()

[]

222

12131 2 3

IIIIx IIIIh

ρ =−−+−−

()()()()

[]

13233 1 2

IIIIx IIIIh

=−−+−−.

Considering the ellipse

1212

AAAA

′′

(Fig. 15.11a), which is entirely travelled through for

II<

, we see that

min

ρ corresponds to the points

A and

′

(

0x =

), while

max

to the points

and

′

(

()( )

13113

/xhIIIIII=− −

); as well, noting that the

ellipse

2323

AAAA

′′

(Fig. 15.11b) is entirely travelled through for

II> , we find that

min

ρ corresponds to the points

A and

′

(

0x = ), while

max

ρ to the points

A and

′

(

()( )

31313

/xhIIIIII=− −). Hence, the arc of helpolhode



max

min

PQP

corresponds to a quarter of the ellipse

1212

AAAA

′′

or of the ellipse

2323

AAAA

′′

, as

II< or

II> , respectively. To a complete travelling through of the polhode P by

the point

P corresponds on the herpolhode H an arc of curve of length



max

min

4PQP

(between corresponding points one has equal lengths on the curves

P and H ), while

the angle described by the radius vector

QP is



max

min

4PQP . If the measure in radians

of the angle



max

min

PQP is not commensurable with π, then the herpolhode is an open

curve; the pole

P does not take again the same position, at the same moment, on the

ellipsoid

E and on the plane Π. If, in particular, the measure in radians of the angle is

commensurable with

π, then the herpolhode is a closed curve.

Taking into account the formula (5.1.16') (see Chap. 5, Sect. 1.1.4 too), we can state

that the double of the areal velocity of the point

P in the plane Π is equal to the

projection on the fixed direction of the moment of momentum

′

K of the moment with

respect to the fixed point

O of the velocity of the point P (calculated with respect to the

same point

O), that is the moment of this velocity with respect to the OQ-axis, given by

(we take into account the formula (15.1.15') and the notations previously introduced)

()()

()

11 22 33

123

223

123

III

hh h K

ωωω

ΩΩ

ωωω

′

⎡⎤

′

⋅×= ,=

⎢⎥

′

⎣⎦

′





Kωω ωω

Consequently, we can write

323

MECHANICAL SYSTEMS, CLASSICAL MODELS

()

[]

()

[]

()

[]

11 22 33

123

23123 31231 12312

///

III

III III III

ωωω

ρκ ω ω ω

Ω

ωω ωω ωω

−−−



in polar co-ordinates

ρ, κ, where we have used Euler’s equations (15.1.40). Developing

the determinant after the last line, it results

() () ()

222

23 31 12

2222222

23 31 12

123

II II II

III

ρκ ωω ωω ωω

Ω

−−−

⎡⎤

=++

⎢⎥

⎣⎦



Taking into account (15.1.56), we can write

()()

123

22 2222

1213

III

IIII

ρκ γ ω ω γ

Ω

⎡

=−−

⎢

−−

⎣



()()

2222

2312

IIII

ωγωγ+−−

−−

()()

2222

1323

IIII

ωγγω

⎤

+−−

⎥

−−

⎦

while, by means of the relation (15.1.69'), we have

()()()

()

[]

{

123

22222

232 3 2

231312

sign

III

II II

KIIIIII

Ω

ρκ δ ρ ρ δ=−−−−

−−−



() ()

[

]

()

[

]

22 22

13 3 2 1 2

sign signII II IIρδ ρδ+− − − − −

() ()

[

]

()

}

22 22

12 1 2 2

signII IIρδ δρ+− − − − .

Effecting the calculations, we obtain the differential equation

()

[

]

222

sign IIρκ Ω ρ δ=+ −



(15.1.71)

where

()()

132

123

I III II

IIII

−− −

(15.1.71')

which determines the angle

κ. We notice that

()

sign 0IIδ −> for

II>

; if

II<

one finds

222

min 1

ρδδ=>. Hence,

0κ >



, the angle κ being thus increasing in

time; the herpolhode surrounds thus the point

Q always in the same sense, attaining

successively the internal and the external circles of the annulus

324

15 Dynamics of the Rigid Solid with a Fixed Point

Eliminating the time between the equations (15.1.70) and (15.1.71), we can write the

differential equation of the herpolhode in the form

()

[

]

()

[]

()

[]

22 2222

12 2 3 2

sign d

sign sign

II II

ρδ ρ

κκ

ρρ δ δ ρ ρ δ

+−

==±

−−−−−

(15.1.72)

One observes thus that between the constants which intervene in this equation take

place the relations

2222

12 3

123

11 1

III

δδδδ

⎛⎞ ⎛⎞

=− =− = −

⎜⎟ ⎜⎟

⎝⎠ ⎝⎠

(15.1.72')

The equation (15.1.72) is with separate variables and can be integrated by a quadrature

with the aid of elliptic functions. The angle

α made by the radius vector QP with the

tangent to the herpolhode (Fig. 15.12) is given by

tan d /dαρκρ= . We notice that

for

min

ρρ= or for

max

ρρ= , hence at the points

min

P and

max

P , respectively, this

tangent tends to infinity; hence, the herpolhode is tangent to the circles which form the

annulus

C. The curvature at a point P is given by

()

222

3/2

2d /d d /d d /d

1d/d

κρρκρ ρ κρ

ρκρ

⎡ + ⎤

⎣⎦

in polar co-ordinates. We study the sign of the numerator of this expression or, which is

equivalent, the sign of the function (we take into account that

d/d 0κρ≠ )

()

21dd d

dd d

κκ

ρρ ρ ρ

⎛⎞

=+ +

⎜⎟

⎝⎠

because the denominator is always positive. Taking into account the equation (15.1.72),

the notations (15.1.70'), (15.1.71') and the relations (15.1.72'), we can write

()

()()

()

12 3 1

22 22

1213

212

sign sign

IIII

II I I

ρδ ρδ

+−

−−

+− − −

()

()()

()

()()

()

23 1 2 31 2 3

22 22

2312 1323

232

sign

II I I II I I

IIII IIII

δρ ρδ

+− +−

−− −−

−−−

By reduction to a common denominator, one finds that the numerator is a polynomial of

second degree in

ρ (the coefficient of

ρ vanishes), which has two real zeros (we

notice that

()

= ). Because

222

max

min

ρρρ<< (excepting the points of tangency

with the circular annulus, for which we have equality), where

min 1

ρδ=

for

II<

325

MECHANICAL SYSTEMS, CLASSICAL MODELS

(we have

δδ< too, in conformity to the formula (15.1.72'), while

()

sign 1II−=−) and

min 3

ρδ= for

II> (we have

()

sign 1II−= too),

while

max

ρδ= , it results that

()

ρ > for any point of the herpolhode; in

conclusion, this curve has always the concavity directed towards the fixed point

(hence without points of inflection, as it has been stated by Poinsot in his memories).

15.1.2.7 Permanent Rotations

We notice that the system (15.1.40) has three obvious systems of particular solutions

ωω= ,

const

ω = , 0

ωω==, ijki≠≠≠, ,, 1,2,3ijk= ,

(15.1.73)

which must correspond to the initial conditions. If, e.g., we consider the solution

ωω= ,

0ωω==, this one must verify the system (15.1.40) at any moment t,

hence also at the initial moment; thus, the initial conditions must be of the same form.

In this case, the theorem of existence and uniqueness ensures that the motion of the

rigid solid is a uniform (finite) rotation about the

Ox -axis (

constω==





iω );

because the derivative with respect to time of the vector

ω is the same in the two frames

of reference (

′

and R ), it results that the vector ω is constant also with respect to

the inertial frame (the direction of the

Ox -axis remains constant with respect to this

frame too). Analogously,

ω= iω and

ω= iω , respectively, can represent uniform

rotations about the corresponding axes if the initial conditions are compatible with these

solutions. The respective axes of rotation are called permanent axes of rotation, the

corresponding rotations being permanent rotations. This result corresponds to the

Theorem 14.2.1, obtained as a particular case of motion of the rigid solid about a fixed

axis.

We consider now the permanent rotations as limit cases of the general results

obtained above, corresponding to the situation in which the inequalities concerning the

position of the constant

I with respect to the principal moments of inertia (not equal one

to the others) become equalities. Thus, if

II= , then the relation (15.1.66) leads to

() () 0ttωω==, because

II≠ and

II≠ , while the second relation (15.1.49)

shows that

() consttωΩ== ; moreover, the relations (15.1.48') lead to the same

result (the last relations can take place only if

0ω = , while the first relations lead to

0ω = ). We are thus in the case (15.1.73) for 3i = ,

1j =

and 2k = . As we have

seen, the

Ox -axis is fixed with respect to the rigid solid (hence with respect to the

frame of reference

R too) and with respect to the fixed frame

′

. From (15.1.58) it

results

sin sin sin cos 0θϕ θϕ==, cos 1θ = , hence 0θ = ; the angle ϕ, as well as

the angle

ψ given by (15.1.59'), will be arbitrary (the planes

Ox x

′′

and

Ox x are

superposed). Thus, the

Ox -axis coincides with the

′

-axis, the support of the

moment of momentum

′

K ; the formula (15.1.46) leads to the same result if we make

ωω Ω==, noting that ω and

′

K have the same direction (including the same

326

15 Dynamics of the Rigid Solid with a Fixed Point

sense). We can choose the angle

ψ arbitrarily ( () consttψ = , eventually 0ψ = ), the

angle

()

()tttϕΩ ϕ=−+ corresponding to a uniform rotation about the fixed axis

(Fig. 15.13a). We have seen that, in this case, the polhode is reduced to the points

and

′

at which the polhodic cone, degenerated into a straight line along the major

axis of the ellipsoid of inertia pierces this ellipsoid. Because we are in the case

II< ,

it results that

min 1

0ρδ==,

max

0ρδ==, so that the herpolhode is reduced to the

point

A (or to the point

′

), the plane Π being tangent to the ellipsoid at this point.

Fig. 15.13 Permanent rotations about the fixed axis

′

if it coincides with the

Ox -axis (a), the

Ox -axis (b) or the

Ox -axis (c)

II= , then the relation (15.1.66) leads to

() () 0ttωω==, because

II≠

and

II≠ ; we obtain, analogously,

() consttωΩ== . We find thus again the case

(15.1.73) for

1i = , 2j = , 3k = . The

Ox -axis coincides with the fixed axis

′

because

sin sin 1θϕ= , sin cos cos 0θϕ θ== (so that /2θϕπ== ), the angular

velocity vector

ω being along the moment of momentum

′

K too (in direction and,

obviously, sense). Using the relation (15.1.59'), we notice that the uniform rotation

about the fixed axis specified by the angle of precession

()

()tttψΩ ψ=−+,

corresponding to the initial conditions too (Fig. 15.13b). The polhodic cone is reduced

to a straight line along the minor axis of the ellipsoid of inertia and pierces this ellipsoid

at the extremities

A and

′

of the respective axis; the polhode is thus formed by the

points

A and

′

. Being in the case

II> , we have

min 3

0ρρ==,

max

0ρρ==, the herpolhode being reduced to the point

A (or to the point

′

) and

the plane

Π being tangent to the ellipsoid at this point.

Finally, if

II= , then the notations (15.1.56') lead to

22 2

γγΩ==,

()

22 31231

/IIIIIIγΩ=+−, while the equation (15.1.57') becomes

()

2222

ωΩ γΩ=± − −

327

MECHANICAL SYSTEMS, CLASSICAL MODELS

so that

222

Ωωγ≤≤. We denote

222 22

cos sinωΩ χγ χ=+, 0 χπ≤≤ (as a

matter of fact,

χχπ≤≤

0χ ≥

); it results (we have taken the sign + before the

radical, corresponding to an increasing of

)

sin

()()

1223

IIII

λγΩ Ω

−−

=−= .

By integration, we have

ln tan ( )

λτ=+

ln tan

=−

wherefrom

()

tan e

tλτ

= ,

()

22 22 2

tanh ( )tωγ γΩ λ τ=− − +.

(15.1.74)

Then, the relations (15.1.56) lead to

cosh ( )t

λτ

222

tanh ( )tωΩ λ τ=+,

cosh ( )t

λτ

(15.1.74')

where we took into account (15.1.49') and we noticed that

ββΩ==. In the

hypothesis in Sect. 15.1.2.1 (

()

0tω > ,

()

0tω < ,

()

0tω > ) we have

()

cosh ( )

λτ

=−

() tanh ( )ttωΩλτ=+,

()

cosh ( )

λτ

(15.1.74'')

observing that the pole

P travels through an arc of ellipse in an infinite time

(

lim 0 0

→∞

=−,

lim 0 0

→∞

=+,

lim 0

ωΩ

→∞

=−), stopping at the point

A .

Starting from (15.1.51) and making

p λ= , 1k = ,

βΩ= , it results

ωΩ

−=

−

∫

wherefrom, by a change of variable

tanhz κ= , we find again the above results (we

use the relations (15.1.49'') too). We notice that, for

t →∞, the relations (15.1.58),

(15.1.59') lead to

sin sin 0θϕ→ , sin cos 1θϕ→ , ψΩ→



, wherefrom /2θπ→ ,

0ϕ → ,

()

ttψΩ ψ→−+ (we have put in evidence the initial conditions too);

thus, the

Ox -axis tends to the fixed axis

′

(being thus also a fixed axis), the

rotation taking place about the moment of momentum

′

K (Fig. 15.13c). If the initial

conditions correspond to the motion determined for

t →∞, then we obtain a

328

15 Dynamics of the Rigid Solid with a Fixed Point

permanent rotation of the form (15.1.73) about the mean axis of the ellipsoid

E (the

mean principal axis of rotation) for

2i = ,

3j =

, 1k = .

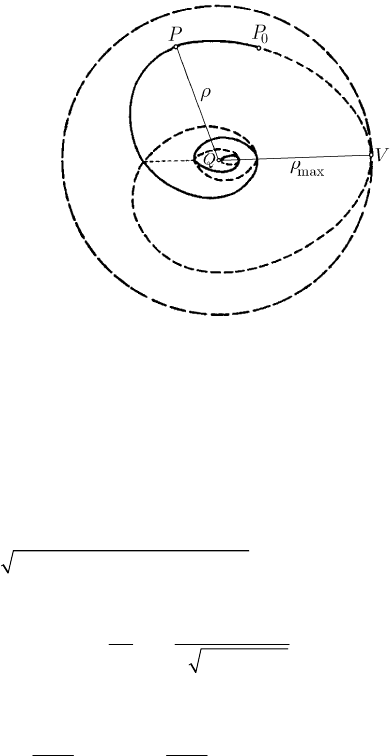
Fig. 15.14 The double spiral of a herpolhode in the limit case in which

the circular annulus is reduced to a circle

We have seen, in this case, that the polhode is formed by two ellipses (

ε and ε

′

contained in the planes (15.1.68) in which degenerates the polhodic cone; as a matter of

fact, the case which corresponds to the formulae (15.1.74'') leads to an arc of ellipse

ε,

the sense of travelling through towards the point

A being that indicated in Fig. 15.10.

In what concerns the herpolhode, we notice that

min 1 3

0ρδδ===, while

()()

max

21223123

/KI I I I IIIρδ== − − , hence the circular annulus is reduced

to a circle. The equation (15.1.72) of the herpolhode becomes (we have

0δ =

)

max

hκ

ρρ ρ

=±

−

By integration, we get

()

(

)

max max

cosh

ρρ

κκ

=± −

(15.1.75)

329

MECHANICAL SYSTEMS, CLASSICAL MODELS

hence a double spiral, with an axis of symmetry, which tends asymptotically towards

the point Q (the vertex V corresponds to

max

ρ , being the only point of tangency with

the circle) (Fig. 15.14).

As a matter of fact, the point P travels through only an arc of spiral, from the point

P (corresponding to the initial position) till the asymptotic point Q (to which the pole

arrives in an infinite time, although the length of the spiral is finite), through which

passes the rotation axis.

In conclusion, in the particular case in which the rigid solid begins to rotate about a

principal axis of inertia, corresponding to the fixed point, this motion continues

indefinitely; the axis of rotation is fixed in the solid and in the space (with respect to the

frames of reference

R and

′

, respectively). Assuming now that /

ωω, 1,2, 3i = ,

are the constant direction cosines of an arbitrary permanent axis of rotation Δ with

respect to the frame of reference

R, the formula (15.1.47'') shows that constω = , so

that the components

ω , 1, 2, 3i = , must be constant too; Euler’s equations (15.1.40)

become

()

2323

0IIωω−=,

()

3131

0IIωω−=,

()

1212

0IIωω−=,

and hold only if two of the components of the vector ω vanish (if the principal moments

of inertia are distinct). Hence, the principal axes of inertia are the only instantaneous

axes of rotation which remain fixed in the rigid solid (as well as in space – the frame of

reference

′

). Analogously, imposing the condition constω = (hence 0ω =



), the

relation (15.1.57') shows that we can have only

ωγ= , or

ωγ= or

ωγ= , while

from (15.1.56) it results that we have

0ω =

(as a matter of

fact, to this conclusion leads also the relation (15.1.57)). The equations (15.1.40) show

then that the only axes of uniform rotation are the principal axes of inertia.

Poinsot’s geometric representation allows also an intuitive study of the stability of

the three possible permanent axes of rotation. The quantity I of the nature of a moment

of inertia depends on the initial conditions (15.1.19) for the angular velocity ω. Taking

into account (15.1.48), we have

() () ()

222

20 20 20

11 22 33

222

000

11 22 33

III

ωωω

(15.1.76)

so that

I depends continuously on the initial conditions; if

=ω 0 , then we are in the

case of equilibrium, while

I is non-determinate (it is a quantity of dynamic character).

Let us assume that

0ω >

0ωω==

; in this case

II= , the polhode reducing

to the point

A (if

0ω < , then there corresponds the point

′

) on the ellipsoid E.

By an arbitrary variation of the initial conditions, the point

P moves away from the

point

A (because I will vary with respect to

I ), describing a polhode (closed curve)

around this point. The plane tangent at

P to the ellipsoid of inertia will have a variation

330

15 Dynamics of the Rigid Solid with a Fixed Point

with respect to the plane

Π tangent to the same ellipsoid at the vertex

A , while the

herpolhode will be contained in a circular annulus of non-zero radii. All these variations

are of the same order of magnitude, as it can easily verified (as a matter of fact, as the

polhodic and herpolhodic cones). If we assume that

0ω > ,

0ωω==, then we

have

II= , the polhode being reduced to the point

A on the ellipsoid E ; in case of

an arbitrary variation of the initial conditions we can make analogous considerations.

But if

0ω > ,

0ωω==, then we have

II= , while the polhode is reduced to

the point

A (intersection of the ellipses ε and ε

′

) on the ellipsoid of inertia. To an

arbitrary variation of the initial conditions, the quantity

I will vary with respect to

while the pole

P describes a polhode around one of the points

A and

′

(or

A and

′

), which leads to a corresponding herpolhode; obviously, the variations

corresponding to the polhode and to the herpolhode are no more of the order of

magnitude of the variations of the initial conditions. In conclusion, we can state

Theorem 15.1.11 A permanent rotation about the major or of the minor axis of the

ellipsoid of inertia corresponding to the fixed point represents a stable motion, while a

permanent rotation about the mean axis of this ellipsoid constitutes a labile motion.

We notice that the ellipses

ε and ε

′

(which pierce at the points

A and

′

) divide

the ellipsoid in four zones, each one of them containing one of the points

113

,,AAA

′

. After Bour, one can take as measure of the stability of the rotation about the axis

′

, for instance, the ratio between the area of the zone which contains one of the

points

A or

′

and half of the area of the ellipsoid E. One observes that for

I close

I (hence, for an ellipsoid of inertia close to an ellipsoid of rotation) the area of the

zone which contains the point

A is small with respect to half of the area of the

ellipsoid, hence the considered measure is small, the stability of the rotation about the

Ox -axis being small too.

Projecting the pole

P of the polhode on the plane

Ox x at

P and taking into

account (15.1.15'), we notice that the angle

χ formed by

OP with the

Ox -axis is

given by

132

tan /χωω= (Fig. 15.11b); differentiating with respect to time, we obtain

(

()

111

dtan /d 1 tantχχχ=+



)

23 32

ωω ωω

ωω

−





Using the equations (15.1.40) and then the second equation (15.1.49''), we get, finally,

()

23 2 3

II I

Ω

χω

ωω

−



(15.1.77)

Analogously, if

P is the projection of the pole P on the plane

Ox x , we can write

331

MECHANICAL SYSTEMS, CLASSICAL MODELS

()

12 1 2

II I

Ω

χω

ωω

−

=−



(15.1.77')

for the angle

χ formed by

OP with the

Ox -axis (Fig. 15.11a). It results that

sign signχω=



and

sign signχω=−



. Let us suppose firstly that the stationary

rotation takes place counterclockwise (positive sense) about the

Ox -axis, so that

0ω > , hence that

0χ >



too; in the perturbed motion, the instantaneous axis of

rotation will be rotated about the

Ox -axis in the same sense, so that the pole P will

describe the polhode which surrounds the point

A counterclockwise too. If the

permanent rotation takes place about the

-axis, counterclockwise (positive sense)

too, so that

0ω >

, hence

0χ >



, then, in the perturbed motion, the instantaneous

axis of rotation will rotate about the

-axis clockwise (negative sense). Obviously,

we obtain similar results if we take

0ω <

(see Fig. 15.10 too). Hence, we

can state

Theorem 15.1.12 The permanent rotations about the minor axis and about the major

axis, respectively, of the ellipsoid of inertia corresponding to the fixed point are

different because, in the perturbed motion, the pole of the instantaneous axis of rotation

describes a polhode in the same sense as the rotation of the rigid solid, in the first case,

and in the opposite sense with respect to the rotation of the rigid solid, in the second

case, respectively.

This result can be easily put in evidence with the aid of Maxwell’s top.

15.1.2.8 Case of an Ellipsoid of Inertia of Rotation

In case of an ellipsoid of inertia of rotation (we suppose that the axis of rotation is the

major axis of the ellipsoid,

12 3

IIJII==>>), of equation

()

22 2 2

12 33

Jx x Ix K++ =,

(15.1.78)

the system of equations (15.1.40) is reduced to (we suppose that

0ω > )

0pωω−=



0pωω−=



ωω= ,

constω = ,

()

ω=− .

(15.1.79)

We get thus

0pωω+=



0pωω+=



(15.1.79')

It results (we are in the case

II< , while 0k = , the elliptic functions becoming

circular ones)

() ()

11 02 0

() cos sintptt pttωω ω=−+−,

() ()

22 01 0

() cos sintptt pttωω ω=−−−,

(15.1.79'')

332