Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

15 Dynamics of the Rigid Solid with a Fixed Point

()tθθ= ,

(15.2.14'')

where

is the nutation at the initial moment

tt=

. In this case, the relations (5.2.35)

give the components of the vector

ω along the axes of the movable frame of reference

R in the form

()

1000

() sin sintttωωθω ϕ

′

=−+,

()

2000

() sin costttωωθω ϕ

′

=−+

() costωωθω

′

(15.2.15)

Knowing the components of the tensor of inertia

I with respect to the frame R, the

formulae (15.1.11') allow to calculate the moment of the given forces with respect to the

pole

O, characterizing thus the loading which leads to the considered motion.

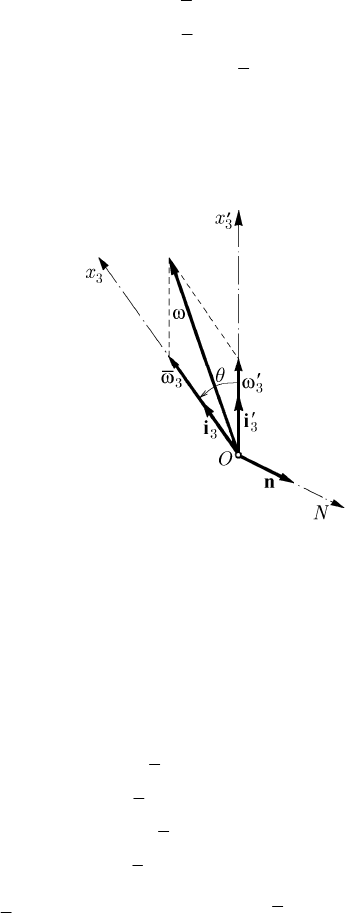
Fig. 15.22 Canonical decomposition of the vector ω in the problem of the regular

precession in the general motion of a rigid solid with a fixed point

In the particular case in which the

Ox -axis is a principal axis of inertia of the rigid

solid

S with respect to the pole O (if

31 32

0II==), we can assume that the axes

Ox and

Ox are the other principal axes of inertia. Replacing the components of the

vector

ω in the relations (15.1.11'') of Euler, we find the components of the moment

M in the form

()()

[

]

000

123 23 0

() cos

Mt I I I I Iωωθω

′′

=−+ −−

()

000

sin cos ttθω ϕ⋅−+

()()

[

]

000

231 13 0

() cos

Mt I I I I Iωωθω

′′

=− + + − −

()

000

sin sin ttθω ϕ⋅−+

()

02 0

12 0 0 0

() sin sin2

Mt II ttωθω ϕ

′

=− − − + .

(15.2.16)

353

MECHANICAL SYSTEMS, CLASSICAL MODELS

If the ellipsoid of inertia is an ellipsoid of rotation with respect to the

Ox -axis (a

prolate spheroid for which

IIJ==), then we are led to

()

[

]

()

0000

3300 00

( ) cos sin cos

Mt I JI ttωωθωθωϕ

′′

=−− −+,

()

[

]

()

0000

3300 00

() cos sin sin

Mt I JI ttωωθωθωϕ

′′

=− − − − +

() 0

Mt= .

(15.2.17)

In this case, the moment

M is in the plane

Ox x (hence,

⊥ ωM ) and one can

easily see that

OOi

M ω⋅= =ωM (hence

⊥ ωM , so that we have

′

⊥ ω

too); hence, the moment

M is directed along the line of nodes ON (Fig. 15.22) and

we can write

()

33 0 0

() cos sin

tIJI

θωω θ

′

⎡⎤

′

=−−

⎢⎥

⎣⎦

()

33 0

cosIJI

′

⎡⎤

′

=−− ×

⎢⎥

⎣⎦

ωω.

(15.2.17')

If the support of the angular velocity vector

ω is close to the

Ox -axis, it results that –

in a first approximation – one can neglect the ratio

/ωω

′

with respect to unity. We

get thus

()

′

=×ωωM ,

(15.2.17'')

a formula useful in various applications; this formula can be used also if

()

/1JI I−<<, becoming an exact one if the ellipsoid of inertia is a sphere.

15.2.1.5 Geometric Representation of the Motion. Jacobi’s Theorem

The first integrals (15.2.1'), (15.2.1'') which appear in the motion of the rigid solid

with a fixed point, in the Lagrange-Poisson case, may be written also in the form

11 22 3

auωα ωα ω α++=

buωω β+=−

ωω=

(15.2.18)

using the notions previously introduced. Let be, as well, a rigid solid

Σ which has a

motion of constant rotation

()

ωω− i ,

constω = , about the axis of dynamical

symmetry of the rigid solid

S; if ω is the angular velocity of the rigid solid Σ with

respect to the inertial frame of reference

′

R , then we have

ωω= ,

()

000 0

33 3

ωω ωω ω=+ − =. We choose the angular velocity

ω so as to have

33 3

IJωω= ; in these conditions, the first integrals (15.2.18) become

354

15 Dynamics of the Rigid Solid with a Fixed Point

11 22

uωα ωα ω α++=,

buωω β+=−,

ωω= ,

(15.2.18')

where we have introduced a new constant

()

2/hI aJβω

⎡

⎤

=−

⎣

⎦

. If, in

particular, the ellipsoid of inertia at the fixed point, in the Lagrange-Poisson case, is a

sphere, then we have

1a = , the first integrals (15.2.18), (15.2.18'), corresponding to

the motion of the rigid solid

S or of the rigid solid Σ, respectively, having the same

form.

The motion of the rigid solid

Σ, considered independent of the rigid solid S, takes

place as it would be acted upon by its own weight, its ellipsoid of inertia being a sphere.

We can thus state that, in general, the motion of a heavy rigid solid with a fixed point,

in the Lagrange-Poisson case, may be obtained by the composition of the motion of a

heavy rigid solid for which the ellipsoid of inertia is a sphere with a motion of constant

rotation about the axis of symmetry of the ellipsoid of inertia of the considered rigid

solid. Research concerning the geometric representation of the motion is due to C.G.J.

Jacobi, E. Lottner, J.J. Sylvester, N.B. Delone etc.

Using the theory of conjugate motions in the sense of Darboux, one can show that

the motion of a heavy rigid solid

Σ with a fixed point, for which the ellipsoid of inertia

is a sphere, may be obtained by the composition of a motion of Poinsot type with an

inverse motion of Poinsot type. The demonstration of this theorem is particularly

arduous; one puts in evidence, in a constructive form, the two motions, with arbitrary

initial conditions.

We notice that the motion of rotation of the rigid solid

S with respect to the rigid

solid

Σ may be considered as a motion of rotation about the normal to the fixed rolling

plane in the motion of Poinsot type, component of the motion of the rigid solid

Σ.

Taking into account Sylvester’s theorem (see Sect. 15.1.2.10), we can show that, by the

composition of the motion of rotation considered above with a motion of Poinsot type,

one obtains a motion of Poinsot type too. The previous results allow to state

Theorem 15.2.2 (Jacobi) In general, the motion of a heavy rigid solid with a fixed

point, in the Lagrange-Poisson case, can be obtained by the composition of a motion of

Poinsot type with an inverse motion of Poinsot type.

Studies in this direction have been made by E. Padova, G.H. Halphen, G. Darboux,

W. Hess, E.J. Routh, R. Marcolongo, A.G. Greenhill and F. Kötter too.

15.2.2 The Sonya Kovalevsky Case

In 1888, a century after Lagrange’s researches of 1788, Sonya Kovalevsky has been

awarded by the Academy of Sciences of Paris for her studies concerning what we call

now the Sonya Kovalevsky case (considered as the IIIrd case of integrability). In this

case, the ellipsoid of inertia is of rotation, the centre of mass

C is situated in its

equatorial plane, the squares of the semi-axes in this plane being half of the square of

the semi-axis corresponding to the axis of symmetry (

12 3

2II I== ,

0ρ = , the

ellipsoid of inertia being a prolate spheroid); without any loss of generality (the axes in

355

MECHANICAL SYSTEMS, CLASSICAL MODELS

the equatorial plane are equivalent from the point of view of the properties of inertia),

we can assume that

0ρ = , the centre C being thus situated on the

Ox -axis.

After obtaining the fourth first integral found by Kovalevsky, one passes to the

systematic determination of the components of the angular velocity vector

ω and to the

specification of the position of the rigid solid with respect to the inertial frame of

reference.

15.2.2.1 First Integrals of the Motion

In the Sonya Kovalevsky case, the equations (15.1.21) read

123

20ωωω−=



231 3

2ωωωγα+=



ωγα=−



, (15.2.19)

with

/constMg Iγρ==, while the first integrals (15.1.42)–(15.1.44) take the

form

()

11 22 33

22ωα ωα ωα Ω++=,

()

22 2

12 3 1

22ωω ω γαγ++=− −

222

123

1ααα++=,

(15.2.20)

where we have introduced the constants

KIΩ

′

/hIγ = .

Amplifying the second equation (15.2.19) by

i1=− and summing with the first of

these equations, we obtain

()()

12 312 3

2iiii

ωω ωωω γα++ +=

Proceeding analogously with the equations (14.1.54), we may write

()()()

12 312 312

ii ii i

αα ωαα αωω++ += +

If we eliminate

α between these relations, then we get

()() ()()

12 12 312 12

iiiii

ω ω γα α ω ω ω γα α+−+=− +−+

⎡⎤⎡⎤

⎣⎦⎣⎦

()()

12 12 3

ln i i i

ωω γαα ω+−+=−

⎡⎤

⎣⎦

Replacing

i by −i, we obtain an analogous relation; eliminating

ω between this relation

and the previous one, it results

()()()()

12 12 12 12

ln i i i i 0

ωω γαα ωω γαα+−+ −−−=

⎡⎤⎡⎤

⎣⎦⎣⎦

356

15 Dynamics of the Rigid Solid with a Fixed Point

Integrating, we get a fourth algebraic first integral (the Kovalevsky integral)

()()()()

12 12 12 12 0

iiiiωω γαα ωω γαα γ+−+ −−−=

⎡⎤⎡⎤

⎣⎦⎣⎦

constγ = ,

(15.2.21)

which can be written also in the form (separating the real parts from the imaginary ones

in the right parentheses, one obtains a product of sum by difference)

()

22 2

12 1 12 2 0

2ωωγα ωωγα γ−− + − =.

(15.2.21')

The constants

γ,

and

γ introduced above have the dimension of an angular

acceleration, while the constant

Ω has the dimension of an angular velocity.

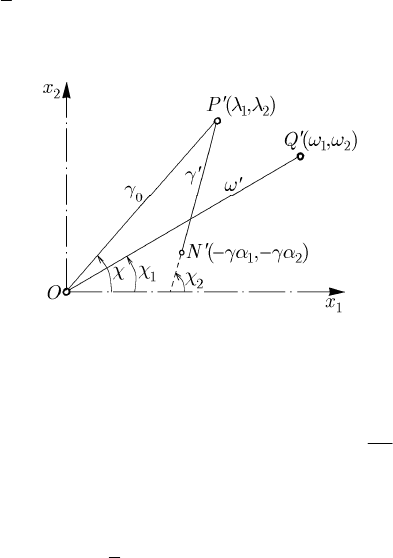
Fig. 15.23 The angle χ in the Sonya Kovalevsky case of integrability

Introducing the notations

112 1

λωωγα=−−,

2122

2λωωγα=−,

λω=+

(15.2.22)

we can express the first integral of the mechanical energy and the Kovalevsky integral

in the form

λλ γ−=,

22 2

12 0

λλ γ+=.

(15.2.22')

We notice thus that the trajectory of the representative point

P of co-ordinates

123

,,λλλ

is the intersection of a circular cylinder with a plane, hence an ellipse. The

components of the velocity of this point are

132

λωλ=



231

λωλ=−



332

λωλ=



(15.2.22'')

where we took into account the equations (14.1.54) and (15.2.19); therefore, we obtain

()

22 2

12 12 3 1 2 0 3

λλ λλ ω λ λ γ ω−=− +=−



. Projecting the point P along the generatrix

of the cylinder at

′

, on the plane

Ox x , we introduce the angle χ made by the radius

357

MECHANICAL SYSTEMS, CLASSICAL MODELS

′

with the

Ox -axis (Fig. 15.23); observing that

tan /χλλ= and differentiating

with respect to time (we have

()

d tan /d 1 tantχχχ=+



), we get

χω=−



. (15.2.22''')

Hence, the motion of the point

′

takes place as this one would be at the end of a rigid

bar of length

a, articulated at the fixed point, in the equatorial plane (considered to be

perfectly smooth) of the ellipsoid of inertia. The point would participate to the rotations

ω and

ω , without being involved in the rotation

ω ; the angular velocity of the bar

with respect to the rigid solid is thus

ω− i .

Let

N be the extremity of the vector

′

− i and N

′

the projection of this point on the

Ox x

-plane; in this case,

11 2

cosλγα γ χ

′

+= ,

22 2

sinλγα γ χ

′

+= , where

||NPγ

′′′





, while

()

,NP Oxχ

′′







. As well, let Q be the extremity of the vector

ω applied at O and

′

its projection on the

Ox x

-plane; denoting ||OQω

′′





and

()

,OQ Oxχ

′







, it results

cos2 cosωχγχ

′′

sin 2 sinωχγχ

′′

. One

obtains thus

ωγ

′′

2χχ= .

(15.2.23)

The third relation (15.2.22) and the relations (15.2.23) allow to write

()

33 2

221cosωλγ χ

′

=− +

(15.2.23')

Using the relations (5.2.35), (5.2.36), we may express the first two first integrals

(15.2.20) by means of Euler’s angles; we get

()

2 sin cos cos 2ψθϕψθθΩ++ =





()

2sin cos2sinsinθψ θ ϕψ θ γ θ ϕγ+++=− −







(15.2.24)

As well, the Kovalevsky first integral may be written in the form

()

222

sin cos 2 2 sin sin 2 sin sinθψ θ ϕθψθ ϕγθϕ−+−

⎡

⎤

⎣

⎦



()

222 2

2 sin cos2 sin sin 2 sin cosθψ θ ϕ θ ψ θ ϕ γ θ ϕ γ+−−−=

⎡⎤

⎣⎦



wherefrom

()()

222 222

sin 2 sin sinθψ θ γθψ θ ϕ++−

⎡

⎣



22 2

2 sin cos sin sinθψ θ ϕ θ γ θ γ−+=

⎤

⎦



(15.2.24')

358

15 Dynamics of the Rigid Solid with a Fixed Point

Thus, we have at our disposal three differential equations for the three unknown

functions (Euler’s angles).

The system of equations (14.1.54), (15.2.19) contains the time only under the

differential operator; taking into account the results in Sects. 15.1.1.4 and 15.1.1.5, we

can affirm that this system, of the form (15.1.22), may be replaced by a system of only

five differential equations, of the form (15.1.24), for which we know the four first

integrals (15.2.20), (15.2.21'). Using Jacobi’s last multiplier theory, one obtains the fifth

first integral. Hence, the complete system of first integrals of the system of equations

(14.1.54), (15.2.19) is obtained with the aid of two quadratures. Euler’s angles

θ and ϕ

are then given by the relations (5.2.36) in the form

arc cosθα= ,

arctan

= ,

(15.2.25)

while the angle

ψ results from the third relation (5.2.35) (we use the equations (14.1.54)

and the first first integral (15.2.20))

()

12 21

cos

αα αα

ψωϕω

θα

αα

−

⎛⎞

=−=−

⎜⎟

⎝⎠





()

33 3

11 22

22 2 2

12 3

/2 /2 cos

1sin

Ωωα Ω ω θ

αω αω

αα α θ

−−

===

+−

(15.2.25')

by a quadrature.

The general problem put by Sonya Kovalevsky has been considered again by N.E.

Jukovskiĭ, G.K. Suslov, F. Kötter, G.V. Kolosov and W. von Tannenberg; the particular

case

0γ = has been studied by N.B. Delone, G.G. Appelrot and B.K. Mlodzevenski.

Various researchers hoped that one can use the method introduced by Kovalevsky also

for other problems, expressing – conveniently – the given conservative forces by means

of certain potential functions; but E. Padova showed in 1895 that this is not possible,

the problem being always reduced – from the mathematical point of view – to the

problem studied by Kovalevsky.

15.2.2.2 Changes of Variables

The problem is put to give to the first integrals a convenient form, so that the two

quadratures which must be effected have a much simpler form. Introducing the complex

variables

11 2

ix ωω=+,

21 2

ix ωω=−,

11 2

iξλ λ=+,

21 2

iξλ λ=−, (15.2.26)

Sonya Kovalevsky succeeds to express all the searched quantities by means of some

hyperelliptic functions of the first kind. Therefore, it results

112

2 xxω =+,

()

221

2ixxω =−,

112

2λξξ=+,

()

221

2iλξξ=−,

and the relations (15.2.22) give

359

MECHANICAL SYSTEMS, CLASSICAL MODELS

()

112 12

2 xxγα ξ ξ=+− + ,

()

221 21

2i ixxγα ξ ξ=−−−.

Taking into account the first two equations (15.2.19), we find the differential equations

which are verified by the functions

()xxt= and

()xxt= in the form

131 3

2ixxωγα=−



232 3

2ixxωγα−= −



. (15.2.26')

The first integrals (15.2.20) take the form

()( )

12 1 2 12 21 3 3

2xx x x x xξξγωαγΩ+− + + = ,

()()

12 12 3

2xx ξξ ω γ+−++=,

()

22 2 2 2 2 2 2

12 12 21 3 0

xx x xξξγαγγ−++=−,

(15.2.27)

where we took into account the Kovalevsky integral

12 0

ξξ γ= .

(15.2.27')

We amplify successively the first two equations (15.2.27) by

2x− ,

()

xx−+ and by

1212

,,xxxx, respectively; summing then with the third equation

(15.2.27), we obtain

()

() ( )

31 3 1 1 1 2

xPxxxωγα ξ−= +−

()

() ( )

32 3 2 2 1 2

xPxxxωγα ξ−= +−,

()()

()

31 3 32 3 1 2

,xxRxxωγαωγα−−=,

(15.2.28)

where we have denoted

() 2Px Ax Bx C=++,

() ( )

12 12 1 2

,Rx x Axx Bx x C=+++,

()

2Axxγ=− + ,

()

12 1 2

2BxxxxγΩ=− + + ,

2222

012

Cxxγγ=−− .

(15.2.29)

Eliminating

ξ and

ξ between the first two equations (15.2.28) and the equation

(15.2.27'), we find

()

() ( )

31 3 1 32 3 2 0 1 2

xPxxPxxxωγα ωγα γ−− −− = −

⎡⎤⎡⎤

⎣⎦⎣⎦

. (15.2.28')

From this equation and the third equation (15.2.28), we can express the binomials

31 3

xωγα− and

32 3

xωγα− as functions of

x and

x , finding thus the differential

equations of first order verified by the functions

()xxt= and

()xxt= .

Eliminating the above mentioned binomials between the relations (15.2.28) and taking

into account (15.2.27'), we find the relation

360

15 Dynamics of the Rigid Solid with a Fixed Point

() () ( ) ( )

12 21 012 12

,Px Px x x Qx x B ACξξγ++−= =−

(15.2.30)

The identity

()()( )()()

1 2 1 2 12 12

,,Px Px x x Qx x R x x+− =

(15.2.30')

holds too.

The equations (15.2.27') and (15.2.29) may be written also in the form

()

[

]

()

[

]

()( )

12 21 12012

,Px Px Qx x x xξξ γ+=−−,

12 0

ξξ γ= ,

wherefrom

() ()

[

]

()

12 21 12

,Px Px Qx xξξ±=

() () ()

120012

2 Px Px x xγγ±−−.

We may write

() ()

()()

12 1020

12 12

Px Px

xx xx

ξξ γγ

⎡⎤

±=±

⎢⎥

−−

⎣⎦

∓

()

12 0 1 2 0

ww w wγγ=± −−

(15.2.31)

too, where

()

() ()()

[]

1,2 1 2 1 2

,w Rx x Px Px

=±

−

(15.2.31')

are the roots of the equation (we take into account also the identity (15.2.30'))

()

12 12

Rx x Qx x

xx xx

−+=

−−

(15.2.31'')

which has always real roots for

,xx complex conjugate numbers.

15.2.2.3 Reduction of the Problem to Ultraelliptic Integrals

We introduce also the polynomial

42 22

() 2 4Px x x xγγΩγγ=− + − + − ,

(15.2.29')

which has the properties

() ()

Px Px= , 1, 2j = . Following Weierstrass’s theory

concerning the elliptic integrals, one can verify the relations

361

MECHANICAL SYSTEMS, CLASSICAL MODELS

() () ()

12 1

dd d

xx s

Px Px s

−+ = ,

() () ()

12 2

dd d

xx s

Px Px s

(15.2.32)

where

()

22 22

() 2sssϕγγγγΩ=−+−−

⎡⎤

⎣⎦

(15.2.32')

is the Euler resolvent of the equation

() 0Px = and where we have introduced Sonya

Kovalevsky’s variables

swγ=+,

swγ=+. (15.2.32'')

The zeros

123

,,eee of the polynomial ()sϕ can be expressed by means of the zeros

123

,,,εεεε of the polynomial ()Px in the form

()

112

εε=+,

()

213

εε=+,

()

εε=+.

(15.2.33)

We mention that one may use the Aronhold resolvent too in the form

() 4ssgsgψ =−−,

()

22 2

γγ γ=− − + ,

()

22 22 3

327

γγ γ γΩ γ=− − + −

(15.2.34)

Starting from the equations (15.2.31) and using the Kovalevsky variables and the

notations

e γγ=+ ,

e γγ=−, (15.2.33')

we obtain

()

()()

()

11212

sese sese

ξ =− −+− −

−

()

()()

()

21212

sese sese

ξ =− −−− −

−

(15.2.35)

Noting that

()()

()

()()

12 12

Px Px

ww ss

=− =−

−

and taking into account the relations (15.2.35) and the identities

362