Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

16 Other Considerations on the Dynamics of the Rigid Solid

()

13 23

JIJ Mωωω+− =



()

23 31

JIJ Mωωω−− =



IMω =



(16.1.1)

where

M is the moment of the given external forces with respect to the centre of the

mass of the Earth.

Assuming, in a first approximation, that

=M0 it results the system of equations

0nωω+=



0nωω−=



−

=>,

(16.1.2)

where we took into account that

constωω== ,

0ω > . Hence, the Earth has a

uniform motion of rotation about the

Ox -axis, with a constant angular velocity

rad/h rad/day,0.0000729rad/s 0.0043753rad/min 0.2625161 6.3003876ω == ==

effecting a complete rotation in a mean solar time

T πω=

86164.098s=

23h56min04.098s= 0, equal to a sidereal day. The equatorial velocity of the Earth is,

in this case, given by

0.0000729 6378246m/s 465.11m/s

vaω== ⋅ ≅ , where

is the semi-diameter of the terrestrial spheroid at the equator. This motion of the Earth

has been put in evidence by various experiments, e.g.: the deviation towards the east

point in the free falling to the surface of the Earth (see Chap. 10, Sect. 2.2.8), Foucault’s

pendulum (see Chap. 10, Sect. 2.2.10) etc.; as well, in the last time, direct observations

in the cosmic space have been made.

The two differential equations can be written also in a unitary form

i0nωω−=





iωω ω=+



, i1=−,

wherefrom

ωκ=

, κ ∈ ^ ; we get

()

() costntωω γ=−,

()

() sintntωω γ=−,

(16.1.2')

where the constants

and γ may be determined by means of the initial conditions

10 1

()tωω= ,

20 2

()tωω= , obtaining

()()

000

ωωω=+,

arctannt

=− .

(16.1.2'')

As it has been shown in Sect. 15.1.2.8 too, it can be seen that the corresponding motion

is a regular precession with the period

2/Tnπ= . The instantaneous axis of rotation

describes the polhodic cone around the

Ox -axis, with the angular velocity n;

383

taking

()

/ 1/ 306IJI−=, we find

()

/1/305IJJ−≅, so that

0.0207rad/dayn ≅ . We notice that

()

2/ /TJIJπω=−

()

[

]

//305

TIJJ T=−=; hence, the polhodic cone will be entirely described’ in

305 sidereal days (hence in 304 days 4h 49.89s mean solar). This period is known as

Euler’s cycle.

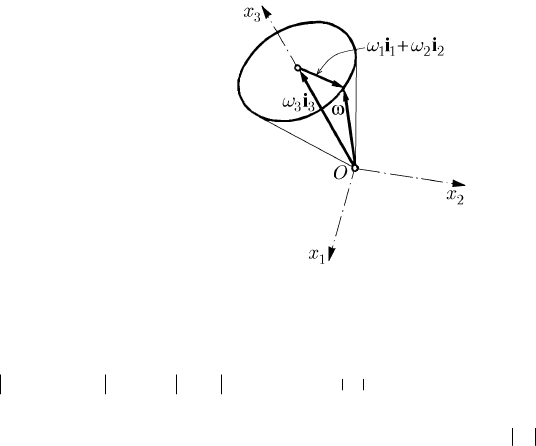
Fig. 16.2 The motion of precession of the extremity of the vector ω

The motion of precession of the extremity of the vector ω on a director circle of the

polhodic cone is put in evidence in Fig. 16.2, taking into account that

11 22

ωω ω+=ii

33 3

ωω=i

, hence const=ω . The intersection of the Earth’s

oblate spheroid with the polhodic cone will be also a circle, called Euler’s circle.

Introducing a vector

n= iΩ along the

Ox -axis, so that

n=Ω

, the system of

equations (16.1.2) may be written in the vector form (

ω= iω )

=×



ωΩω

(16.1.2''')

too. We find thus the equation of motion of a vector ω of fixed origin and constant

modulus, which describes a cone around a direction specified by the vector Ω, with an

angular velocity Ω (in our case

nΩ = , corresponding to a regular precession).

Observations made with the greatest precision, corresponding to a much more

complex modelling of the Earth (which takes into account the displacement of masses

of air, the deformability of the Earth, which assumes that it is elastic etc.), show that the

positions of the poles are not fixed on its surface (the axis of rotation of the Earth does

not coincide with the axis of the geographic poles). Thus, instead of Euler’s period of

approximate 10 months, one finds a period of 14 months (Chandler's period). One sees

that the displacement of a pole on the surface of the Earth can be obtained by the

composition of this periodic displacement with another displacement having a period of

one year (due to the displacement of the masses of air at the surface of the Earth, to the

loading of the continents with masses of snow and to other phenomena, with an annual

period); the positions of the pole are contained in the interior of a square of 20 m side.

MECHANICAL SYSTEMS, CLASSICAL MODELS

384

16 Other Considerations on the Dynamics of the Rigid Solid

Phenomena analogous to those exposed at the preceding subsection take place in the

microcosmos too. Let thus be a system

S of particles P loaded with electric charges of

the same sign, which have a finite motion in a central field; we assume that at the centre

of the field stays a charge considered to be fixed, the motion taking place with respect

to it. We suppose also that this system is situated in a homogeneous and constant

exterior magnetic field, characterized by the magnetic induction

B. Such a system is,

e.g., an atom placed in a magnetic field; the fixed charge is the nucleus, the electrons

being the charges in motion. Assuming that all the particles in motion have the same

specific charge

/em, e being the electric charge and m the mass, one obtains a motion

quite simple but particularly important in atomic physics.

The magnetic moment of the current distribution can be expressed in the

form

(/2 )

emK , where

is the moment of momentum of the considered motion,

of constant modulus, applied at the point

O, where we assume that the nucleus of the

atom (the fixed charge) stays. The magnetic field is uniform, so that the resultant of the

forces which act upon the system

S vanishes, its moment being given, with a good

approximation, by

(

)

(

)

OO O

×= × =×KBK B KΩ

=− BΩ

The theorem of moment of momentum reads

=×



KKΩ

(16.1.2

)

and is a relation of the form (16.1.2"'). We are thus led to a mechanical-magnetic

analogy which allows to state that the moment of’ momentum

describes a cone

(analogue to the polhodic cone) with a retrograde regular precession, called the Larmor

precession; the corresponding angular velocity

(/2 )emB=Ω is called the Larmor

pulsation. Because

0e <

for electrons, the motion of rotation takes place

counterclockwise about the support of the vector

We notice that the introduction of the moment

× KΩ is entirely justified in case of

a permanent magnetic dipole, the magnitude of which is independent on the orientation

of the system

S. The approximation of calculation remains very good even in the

absence of rigid links, in case of a weak magnetic field (

≅B0).

The velocity of precession of the vector

K can be measured experimentally by

using the Zeeman effect, resonance methods etc.

16.1.1.4 Calculation of the Regular Precession. The Secular Variation

The hypothesis made in the preceding subsection, in conformity to which

=M0 is

correct only if the external forces which act upon the Earth are reduced to a resultant

which passes through the point

O. Taking into account that the Earth is an oblate

spheroid with the minor axis along the

-axis, one sees that

≠M0

. Indeed,

taking into account only the attraction of the Sun, the two halves in which the Earth is

16.1.1.3 The Mechanical-Magnetic Analogy. The Larmor Precession

385

bisected by the ecliptic plane have different contributions in the calculation of this

moment (the half over this plane will be acted upon less than the half under it); the

resultant moment will be thus non-zero and, qualitatively, will tend to diminish the

angle of nutation between

′

and

Ox . The components

M ,

1,2, 3i =

, depend on

the relative position of the Earth with respect to the Sun, being periodical functions of

time; they will play the rôle of perturbing terms in the solution of the system (16.1.1),

considered to be homogeneous. The variations of the angles ψ (of precession) and θ (of

nutation) due to some mean values of the moments

M are called secular variations;

expanding these moments into power series, one is led to secular variations of superior

order. As well, one can obtain variations due to moments

M periodic functions of

time (expressed by means of Fourier series), the mean values of which vanish.

To establish the secular variations of the trajectory of a planet

P due to another

neighbouring one

P , one can assume, after Gauss, that the mass of the second planet is

distributed along its trajectory (Kepler’s ellipse); more precisely, one assumes that on

two arcs of ellipse traveled through are distributed equal masses in equal times. In the

case of our interest, we suppose that the mass of the Sun is distributed along its

trajectory; for the sake of simplicity, we approximate the ellipse (which has a very small

eccentricity) by a circle of radius

r , the mass

m of the Sun being uniformly

distributed (a linear density

mrπ ). In the Euler-Poinsot case concerning the

motion of the rigid solid with a fixed point, this one intervenes only by its principal mo-

ments of inertia; we can thus vary the distribution of the masses of the solid, if one

maintains the quantities

J and

I . This property remains valid also in the case of

moments

, 1,2, 3i = , due to perturbing forces which act at a sufficiently great

distance (as it is the distance Earth-Sun with respect to the dimensions of the Earth).

Indeed, the potential of these forces of attraction is in direct proportion to

∫

()()

iiii

rxxξξ=− −

, where

ξ are the co-ordinates of the mass centre of the Sun,

while

x , 1, 2, 3i = , are the co-ordinates of an element of mass dM of the Earth (all

the co-ordinates are considered with respect to the frame of reference

R ), the integral

being extended to the whole mass

M of it. Expanding the ratio 1/r after the powers of

the ratios

xr, 1,2, 3i = , and noting that these ratios are very small with respect to

unity, one obtains a rapidly convergent series. The terms of first degree disappear,

having as factors the integrals

∫

, 1, 2, 3i = , while the terms of second degree

lead to factors of the nature of principal moments of inertia; neglecting the terms of

higher degree, we justify the above statement. In this order of ideas, we replace the

Earth by a system formed by a homogeneous sphere of moment of inertia

with

respect to one of its diameters (with a length equal to the mean diameter 2

R of the

Earth) and a homogeneous material equator of mass

m . In this case,

IImR

=+ ,

/2JI mR

=+ , wherefrom

MECHANICAL SYSTEMS, CLASSICAL MODELS

386

16 Other Considerations on the Dynamics of the Rigid Solid

2IJI

=−

()

mIJ

=−

(16.1.3)

Because of its symmetry, the homogeneous sphere has no one contribution to the

perturbations due to the Sun, remaining only the material equator. The resultant couple

M tends to diminish the angle θ, hence the inclination of the equatorial plane of the

Earth on the plane of the ecliptic, being directed along the axis of nodes, in its opposite

sense (towards the autumnal equinox) (Fig. 16.1). Taking into account the diurnal

motion of rotation of the Earth, this one behaves as a gyroscope, the effect of the

moment

M being, in fact, a gyroscopic effect (this effect will be studied in

Sect. 16.2.1.4).

Assuming, with a good approximation, that the axis of rotation of the Earth is just

the

Ox -axis, the polhodic cone being reduced to this axis (its vertex angle is very

small), we can take the moment of momentum

K along it, with

333

IIω==Kiω .

The rotation angular velocity vector is decomposed in the form (15.2.14) along the axes

′

and

Ox , the vector components being ω (corresponding to the proper rotation)

and

′

(corresponding to the motion of precession), respectively; supposing that these

motions are uniform and that the ratio

()

/IJI− can be neglected with respect to

unity (the factor

()

/cosωω θ

′

being subunitary too), we can assume that the

moment

is given by the relation (15.2.17"). Noting that ωψ

′



, the vector

′

being directed towards the negative sense of the

′

- axis, we can write (Fig. 16.1)

sin

ωθ

=−



(16.1.4)

Fig. 16.3 The retrograde annual precession due to the attraction of the Sun

To calculate the modulus of the moment

M , we will consider the circles (, )OR (in

the terrestrial equatorial plane, corresponding to this equator, of radius approximately

equal to

R, a point P on the circumference being of position vector R) and (, )

Or (in

the plane of the ecliptic, corresponding to the approximate trajectory of the Sun, of

radius

r , a point Q of the trajectory being of position vector

r , so that

=−rr R

(Fig. 16.3). The potential of the force of reciprocal attraction between the points

P and

Q of masses

dm and d

m , respectively, is

387

()

2cos,

SSS

rrRrR=+− rR.

(16.1.5)

Expanding

1/r after the ratio /

Rr, we have (we use the formula of the Newtonian

binomial)

{

() ()

[]

11 1

1cos, 3cos, 1...

SS S

rr r r

⎫

⎛⎞

=+ + −+

⎬

⎜⎟

⎝⎠

⎭

rR rR .

The ratio

Rr is very small, so that the power series is rapidly convergent. The

searched potential is given by

∫∫

(16.1.6)

where the integral is extended to the circles

c and C of radii

r and R, respectively.

We notice that

mm mm=

∫∫

()

cos , d d 0

mm=

∫∫

because of symmetry reasons. To calculate the latter integral, we refer to the frame of

reference

R and we suppose that, in the further calculations, the

-axis coincides

with the line of nodes

ON. We denote by ε and η the angles made by the position

vectors

r and R, respectively, with the

Ox -axis; the co-ordinates of the point Q are

cos

rξε= ,

sin

rξε= ,

0ξ = , while the co-ordinates of the point P are written

in the form

cosxRη= ,

sin cosxRηθ= ,

sin sinxRηθ= . It results

()

cos , cos cos sin sin cos

εη εηθ== +rR

mmε

= ,

dm m

= ,

so that

()

cos , d d cos cos sin sin cos d d

ππ

εη εηθεη

∫∫ ∫ ∫

()

1cos

θ=+.

In this case,

()

13cos1...

fm m

⎡⎤

⎛⎞

=+ −+

⎜⎟

⎢⎥

⎝⎠

⎣⎦

(16.1.6')

MECHANICAL SYSTEMS, CLASSICAL MODELS

388

16 Other Considerations on the Dynamics of the Rigid Solid

Restricting us to these terms in the expansion into a series, one observes that the

equipotential surfaces are circular cones with the vertex at

O, of axis

Ox . The moment

which tends to diminish the angle /2θπ< is given by the forces of attraction

equal to the gradient of the potential

U at an arbitrary point; this gradient is normal to

the equipotential surface, so that the modulus

M is obtained by multiplying the

modulus of the gradient by the distance to the above mentioned point. It results

sin cos

fm m

θθ

∂

M .

Finally, the formula (16.1.4) allows to write (

ωω=

)

03 03

33 3

cos cos

mm R m

Ir r

ψθ θ

ωω

−

=− =−



(16.1.7)

Taking into account that

83 2

6.673 10 cm / g s

−

=⋅ ⋅,

()

/ 1/306IJI−=,

7.29 10 rad / sω

−

=⋅ ,

1.989 10 g

m =⋅,

1.496 10 cm

r =⋅ , 23 27θ

′

, we

get

2.4454896 10 rad / s

−

=− ⋅



7.7172197 10 rad/year

−

=− ⋅ , where we took

into account that

1 sidereal year has 365.2436 mean solar days, 1 mean solar day

having

86400 mean solar seconds; to 1 radian correspond 180 3600/ π⋅

206264.81

′′

≅ , so that we obtain 15.917908

′′

=−



in a mean solar year. We may

thus state that, due to the attraction of the Sun, the Earth has a retrograde annual

precession of approximate

′′

To put in evidence the influence of the attraction of the Moon, we make an

analogous calculation; noting that

7.347 10 g

m =⋅ and

3.844 10 cm

r =⋅ and

taking

23 27θ

′

too (as a matter of fact, the plane of the trajectory of the Moon does

not coincide with the plane of the ecliptic, making an angle of

509

′

with this plane,

the Moon being in an interval of time over this plane and in another interval under it),

we find

34.658192

′′

=−



in a mean solar year, hence a retrograde annual pre-

cession, of approximate

34.7

′′

. Summing the two effects, we get a precession of

50.5761

′′

for a sidereal year. But the above calculations concerning the secular

variations have an approximate character, due to the mathematical model used (Gauss’s

hypothesis, the approximation of the ellipse by a circle, the superposition of the effects,

the non-introduction of other influences etc.). If we compose the Moon-Sun precession

(the displacement of the equinoctial points along the ecliptic) with the planetary

precession (along the celestial equator), then we obtain the general precession (in

longitude), which is now of

50.27 / year

′′

. In this case, the line of nodes ON

describes the whole plane of the ecliptic in

360 3600/50.27 2.5780784 10 years⋅=⋅

, hence in approximate 26000 years, while

the axis of the Earth poles describes the cone of precession (a circular cone of

Ox -axis

and vertex angle

46 54

′

) in the same period of time.

389

16.1.2 Free Nutation. Pseudoregular Precession

We give some general results and then we calculate the free nutation and the

pseudoregular precession in the Lagrange-Poisson case; as well, we make some

considerations concerning the general motions of the Earth.

16.1.2.1 General Considerations

We have put in evidence, in the preceding subsection, a polhodic cone, linked to

Euler’s cycle, which is rolling over a circular herpolhodic cone, the axis of which is the

axis of the ecliptic; as well, we have considered the cone of precession, which can play

the rôle of a herpolhodic cone. We mention that it does not exist one mechanical link

between the polhodic cone with the Eulerian period (for which

=M0,

corresponding to the Euler-Poinsot case, taking place a rolling of the polhodic cone

over the herpolhodic one) and the precession cone with a

26000 years period (for which

the constant moment

≠M0

corresponds to the secular variation which leads to the

Lagrange-Poisson case, where a precession cone intervenes only in a particular case). In

the first case, one obtains an arbitrary nutation (the polhodic cone has a non-

determinate vertex angle), while in the second case the nutation vanishes (

constθ =

hence

0θ =



), because we have taken into account only the secular terms of the

perturbing moment

M ; using the periodic terms too, the nutation would be non-zero

(

0θ ≠



), obtaining thus the nutation of the Earth.

In the Lagrange-Poisson case, the total absence of nutation (

constθ = ) takes place

only if a condition of the form (15.2.11) is fulfilled, so that the polynomial

()Pu have

a multiple solution; if this condition holds only approximately, then the angle

θ is no

more constant, appearing a nutation (

0θ ≠



). In case of the Earth (because of the

secular terms in the expression of the perturbing moment), this nutation is called free

nutation. The nutation due to the periodic terms is called constraint nutation.

16.1.2.2 Calculation of the Free Nutation

To may calculate the free nutation of the Earth, we model the corresponding problem as

a particular Lagrange-Poisson case (a case which differs very little from that of the

multiple root of

()Pu ). Let be thus the problem of the rigid solid with a fixed point O

upon which acts the moment

, of modulus

sin 2

−

(16.1.8)

along the axis of nodes

ON, in its negative sense. As in the Lagrange-Poisson case, we

can use the first integral (15.2.1'), which introduces the spin, as the first integral

corresponding to the theorem of moment of momentum (15.2.1"'). The theorem of

kinetic energy reads

()()

()

22 0

12 32 1 2

cos sin

ωω ω ω ϕω ϕ

⎡⎤

++ =⋅= − +

⎣⎦

ω ,

MECHANICAL SYSTEMS, CLASSICAL MODELS

390

16 Other Considerations on the Dynamics of the Rigid Solid

where we took into account that the vector

M makes the angles πϕ− , /2πϕ− ,

/2π with the axes of the frame of reference R. The second relation (14.1.15) allows

to write

θ⋅=−



MMω

too, an obvious result, corresponding to the rotation in the

Ox x -plane (Fig. 16.1). Introducing the modulus of the moment

M given by

(16.1.8) and integrating with respect to time, we find a third first integral

()()

22 0 2

12 33

cos 2

JIfm h

ωω ω θ

−

++ = +

(16.1.9)

where

h is the constant of energy. Using the relations (5.2.35) and eliminating the

components

ω and

ω , we find again the first and the last equation (15.2.2), to which

we associate

22 2 2

sin coscψθθγ θ+=+



(16.1.10)

with

()

2/hI Jγω

⎡

⎤

=−

⎣

⎦

()

[

]

3/2 / / 0

cfIJJmr=− >; as in the

Lagrange-Poisson case, the constants α and β depend on the initial conditions and the

constants

a and b are functions only of the geometry of the considered mechanical

system, as well as of its mechanical properties.

Proceeding as in Sect. 15.2.1.1, we eliminate



between the first relation (15.2.2)

and (16.1.10); thus, we obtain

()

02222

cos cos sin sinacαω θ γ θ θθ θ−=+ −



Denoting

cosu θ= , it results the differential equation

()uQu= ,

()()

()

22 0

() 1Qu cu u a uγαω=+ − −−

(16.1.11)

wherefrom

()

−=

∫

(16.1.11')

with

cosu θ=

()tθθ= ; one takes the sign + or − before the radical as, at the

initial moment, we have an increasing or a decreasing of the motion. The polynomial

()Qu is of fourth degree, hence the integral (16.1.11') is an elliptic one. As in the

Lagrange-Poisson case,

[

]

012

,uuu∈ ,

()

,1,1uu∈−

being two roots of the

polynomial

()Qu . We obtain thus the free nutation

[

]

,θθθ∈ , the extreme values

corresponding to the roots

u and

u .

391

16.1.2.3 Calculation of the Pseudoregular Precession

Assuming that, at the initial moment

0tt== (for the sake of simplicity, without any

loss of generality), the

Ox -axis is situated along a generatrix of the cone of precession,

we have

23 27 'θ =

0ωω==, while the first integrals (15.2.1'''), (16.1.9) lead

to the relation

cos

KIωθ

′

, as well as to

cosaαω θ= ,

cos 0cγθ+=.

Let be

()

[

]

()

33 3

(3/2) / / /

IJImrεω=−

; it results

caεω=

and

cos 0aγεω θ+=. We can write

()()

()

020

00 0

() 1Quauu uu u auuωε ω=− +−−−

⎡

⎤

⎣

⎦

(16.1.12)

with the new notations. We notice that

uu= is a double zero of the polynomial

()Qu if

()

21 0au uωε −=, which can be assumed with a good approximation

(error of the order of magnitude of

ε, which is very small because of the denominator

r ).

Denoting by

2uu u=+ the zero of the square bracket in (16.1.12), we find the

condition

()()

12uu u u auεω+−+ −

⎡⎤

⎣⎦

() ()

00 0

115

... 0

uu uu

ωε ε

ωω

−−

⎡⎤

=−++=

⎢⎥

⎣⎦

where we have neglected the higher-order powers of

u ; we can assume the

approximate value

()

00 00

1cossinuuu

εε

θθ

ωω

=−=

(16.1.13)

with an error of the order of magnitude

()

()( )

022

00 0

/115au u uεω −−. If

θ is the

value of the angle

θ corresponding to

u , then we have

cos cos 2uθθ=+, 0u > ,

so that

θθθ≤≤. Noting that

()

[

]

()

[

]

10 10

sin /2 sin /2 0uθθ θθ−++= and

assuming that the arc

()

/2θθ− is sufficient small in modulus to can approximate

its sinus, we obtain (as well, we approximate

()

10 0

sin /2 sinθθ θ+≅)

00 0

sin 2

sin

θθ θ θ

=− =−

(16.1.13')

where we have used the approximate relation (16.1.13) too. Because the angle

θ is not

constant, having a variation of amplitude

()

/sincosaεω θ θ, it results a

pseudoregular precession.

MECHANICAL SYSTEMS, CLASSICAL MODELS

392