Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

()

′

+× = − ×

IIMa

OOOO



ωω ω ρ .

(14.1.69')

The equation (14.1.69') specifies the rotation about the point O (the vector ), then the

equation (14.1.69) determines the constraint force

R ; if

()

=MM

123

,, , , , ;

tψθϕω ω ω , then we associate to the vector equation (14.1.69')

the system of scalar equations (14.1.53'') too. We have thus introduced three relations of

finite constraints of the form (14.1.63) (

= 3p , = 0m ) and three scalar components of

the constraint force (

= 3q ).

In particular, if the pole O is fixed, then we have

′′′

===

rva0

OOO

, obtaining the

equations of motion of the rigid solid with a fixed point. If we introduce in these

equations also the influence of the complementary force

′

−

∫∫∫

ra() d

Vμ at the

centre of mass C, then we find again the system of equations (14.1.69), (14.1.69') (one

passes from the action of this force at C to the corresponding torsor at O).

If the point O is constrained to stay on a given perfectly smooth surface S (in

general, movable), then the constraint relation (14.1.67) (

= 1p , = 0m ) is written in

the form

()( )

′′′′

123

;,,;0

OOOO

ftfxxxt .

(14.1.70)

The liberation of constraints axiom leads to a constraint force

=R grad fλ , λ non-

determinate scalar, normal at O to the surface S (the moment

′

); the equations

of motion (14.1.60), (14.1.60') of the rigid solid take the form

()

[]

′′

+× +× +× = +

vv Rgrad

Mfλ



ωωρωρ ,

(14.1.71)

()()

′′

×+×++× =

vvI IM

OOO OO



ρω ωωω.

(14.1.71')

To determine the vector unknowns

′

and and the unknown scalar λ ( = 1q ; 7

scalar unknowns) we have the vector equations (14.1.71), (14.1.71') and the scalar

equation (14.1.70) (7 scalar equations).

As well, if the point O stays on a perfectly smooth curve C (in general, movable),

then the constraint relations (14.1.67) (

= 2p , = 0m ) become

()( )

′′′′

123

;,,;0

lO l O O O

ftfxxxt , = 1,2l .

(14.1.72)

As in the previous case, we can write the equations (14.1.60), (14.1.60') in the form

()

[]

′′

+× +× +× = + +

vv R

1122

grad grad

Mffλλ



ωωρωρ ,

(14.1.73)

()()

′′

×+×++× =

vvI IM

OOO OO



ρω ωωω.

(14.1.73')

233

14 Dynamics of the Rigid Solid

The vector equations (14.1.73), (14.1.73') and the scalar equations (14.1.68) (8 scalar

equations) determine thus the vector unknowns

′

and and the scalar unknowns

and

( = 2q ; 8 scalar unknowns).

Let us suppose that the points O and

of the rigid solid have known motions,

given by the equations

′′

rr()

t ,

′′

()

(14.1.74)

with respect to the inertial frame of reference

′

R ; because the points O and

O are at

an invariable mutual distance (equal to l), the equations (14.1.74) are not independent,

and the relation

′′

−=

⎡⎤

⎣⎦

() ()

ttl

(14.1.74')

takes place. Hence, there remain five independent finite constraint relations (

= 5p

= 0m ). As a matter of fact, the motion of any point

O on the straight line ≡

OOΔ

is determined by the position vector

()

′′ ′′

=+ −

rr rr

OO OO

λ , λ scalar; the case thus

considered is identical to that in which a straight line

Δ rigidly linked to the solid (e.g.,

an axis of the frame of reference

R ) describes a given motion, one of the points of this

axis (e.g., the pole O) having a given motion too. Using the axiom of liberation of

constraints, we introduce the constraint forces

′

R and R

at the points O and

O ,

respectively; the torsor of these forces at the point O is

()

{

}

′′′

+−×

RRr r R

The equations of motion (14.1.60), (14.1.60') are written in the form (the first equation

(14.1.74) allows to calculate the acceleration

′′

aa()

t too)

()

[]

′′

×+× × = − + +

RaRR



ωρ ω ωρ ,

(14.1.75)

()

′′′

+× = − × + − ×

IIMarrR

OOOOOO



ωω ω ρ ,

(14.1.76)

with respect to the non-inertial frame

For the three vector unknowns ,

′

R and R

of the problem (

= 6q

; 9 scalar

unknowns) we can use the vector equations (14.1.75), (14.1.76) and the second

equation (14.1.74), together with the relation (14.1.74') (8 scalar equations). We can

write the constraint relation also in the differential form (the velocity of the point

expressed with respect to the velocity of the point O)

()

′′ ′′

=+× −

vv rr

OO OO

ω ;

(14.1.74'')

14.1.2.3 Rigid Solid Two Points of Which have Imposed Motions

234

MECHANICAL SYSTEMS, CLASSICAL MODELS

a scalar product by

′′

−

leads to an identity, so that there result only two scalar

relations. Hence, the number of unknowns is with a unity greater than the number of

equations, the corresponding system being once indeterminate (as in the case of the

static equilibrium of the rigid solid with a fixed axis).

Choosing the axis

OO as axis

Ox , we can write the equations (14.1.75), (14.1.76)

in components, in the form

()

[]

23 32 1 11 22 33 1 1 1 11

MRMaRRωρ ωρ ω ωρ ωρ ωρ ωρ

′′

−+ ++ − =− ++



()

[]

31 13 2 11 22 33 2 2 2 12

MRMaRRωρ ωρ ω ωρ ωρ ωρ ωρ

′′

−+ ++ − =− ++



()

[]

12 21 3 11 22 33 3 3 3 13

MRMaRRωρ ωρ ω ωρ ωρ ωρ ω ρ

′′

−+ ++ − =− ++



(14.1.75')

()

111 122 313 33 2223 232 3 1312 123

III II I IIωωω ωω ωωωωω+++− + −+ −



()

′′

=− − −

23 12

132

OOO

MMa a lRρρ ,

()

22 2 23 3 12 1 11 33 3 1 31 3 1 2 12 3 23 1

III II I IIωωω ωω ωωωωω+++− + −+ −



()

′′

=− − −

31 11

213

OOO

MMa a lRρρ ,

()

33 3 31 1 23 2 22 11 1 2 12 1 2 3 23 1 31 2

III II I IIωωω ωω ωωωωω+++− + −+ −



()

′′

=− −

321

OOO

MMa aρρ.

(14.1.76')

As well, the condition (14.1.74'') leads to

′′

vvlω ,

′′

=−

vvlω ,

′′

33OO

vv.

(14.1.74''')

The first two equations (14.1.74'''), together with the last equation (14.1.76'), determine

entirely the vector . The last column of the matrix (3.2.11''') allows to specify Euler’s

angles

= ()tψψ and = ()tθθ in the motion of the Δ-line (if we know the direction

cosines of this line with respect to the frame of reference

R ); in this case, the relations

(5.2.35) allow to express the components of the vector as function of the angle of

proper rotation

ϕ. Replacing in the last equation (14.1.76'), this one becomes a

differential equation of second order in

ϕ; by integration, we get = ()tϕϕ and then

= ()

tωω, = 1,2, 3i . The first two equations (14.1.76') determine the constraint

forces

R and

R , while the first two equations (14.1.75') give the constraint forces

′

R and

′

R ; the third equation (14.1.75') specifies the sum

′

313

RR of the last

unknown components, the character of the non-determination being thus put into

evidence. As in the statical case (see Chap. 4, Subsec. 2.1.3), the non-determination is

due to the modelling as a rigid adopted for the solid body.

If the axis

Δ is a principal axis of inertia, the axes

and

having the same

property, we have

===

23 31 12

0III , so that the system of equations (14.1.76')

takes the simplified form

235

14 Dynamics of the Rigid Solid

()

′′

+− = − − −

11 3 2 23 2 3 12

132

OOO

III MMaalRωωω ρρ



()

′′

+− = − − +

22 1 3 31 3 1 11

213

OOO

III MMaalRωωω ρρ



()

′′

+− = − −

33 2 1 12 1 2

321

OOO

III MMaaωωω ρρ



(14.1.76'')

In particular, if the points O and

are fixed, then we have

′′′

===

Oi Oi Oi

vva ,

= 1,2, 3i , while from the conditions (14.1.74''') it results ==

0ωω , =

ωω; we

obtain thus the motion of the rigid solid with a fixed axis.

axis Δ of which passes through this point

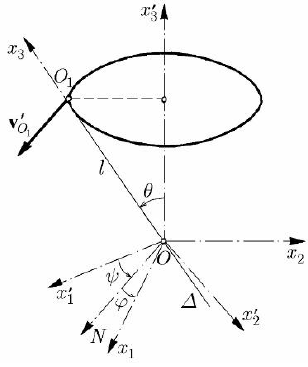
Let us suppose, in particular, that the point O is fixed and that the straight line

describes a circular cone, having a motion of uniform rotation about the cone axis. To

simplify the computation, we take

′

≡OO

, the

′

Ox -axis being the axis of the cone.

The point

O describes a circle in a plane normal to the fixed axis

′

Ox . Introducing

Euler’s angles

ψ, θ, ϕ, the angular velocity of the point

O will be ψ



, so that the

velocity

′

will be directed along the line of nodes ON , having the magnitude

′

sin

vlψθ



(Fig. 14.5); in components, there result

′

sin cos

vlψθϕ



′

=−

sin sin

vlψθϕ



. If we make

′′

vv in (14.1.74''') or if we make = 0θ



(because

= constθ

) in the relations (5.2.35), then we obtain

sin sinωψθϕ



, =

sin cosωψθϕ



, =+

cosωϕψθ



We assume also that the axes

Ox , = 1, 2, 3i , are principal axes of inertia; in this case,

replacing in the third equation (14.1.76'') (we notice that

= constψ



, the rotation being

uniform, and that

′′

aa ), one obtains the equation of motion

Fig. 14.5 Motion of a rigid solid a point O of which is fixed and an

236

MECHANICAL SYSTEMS, CLASSICAL MODELS

sin 2

ΦΦ+=



(14.1.77)

with the notations

2ϕΦ = ,

sin

ψθ

−



(14.1.77')

M (e.g., if the rigid solid is subjected to the action of the own weight, the

axis being a central principal axis of inertia), then the motion of rotation of the rigid

solid is determined only by the angle of proper rotation

()tϕϕ= , which is given by an

equation of the simple pendulum equation type.

More general, we can assume that a frictionless sliding of the rigid solid along the

Δ-axis takes place; the equations of this axis with respect to the inertial frame of

reference

′

R can be written, e.g., in the form (we put in evidence the point Ο on the

Δ-axis)

′′

() ()

xtxtαβ,

′′

() ()

xtxtαβ,

(14.1.78)

intervening thus two finite constraint relations; as above, knowing the motion of the

straight line

Δ, we can consider Euler’s angles ψ and θ as known, so that only the angle

of proper rotation

ϕ remains to be determined. We notice that, due to the frictionless

sliding, the constraint forces

′

R and

are normal to the Δ-axis. We have to

determine eight scalar unknowns

′′ ′

121112

,, , ,

RRR R x , = 1,2, 3i and ϕ, for which we

have eight equations (the equations (14.1.75'), (14.1.76'), where we make

′

313

0RR , and (14.1.78)), the problem being thus determined.

If in the particular problem considered above we have

′

()

OO x t





, then it

results

() ()sin

txtθ

′′



ψ , wherefrom

′′

sin cos

vxψθϕ



′′

=−

sin sin

vxψθϕ



′′

33OO



Observing that

′′ ′

=+×

av v

11 1

OO O



ω , where

′



is the derivative with respect to the

movable frame of reference, using the results previously obtained for the vector and

taking into account that = constψ



, we get

′′ ′

11 1

13 3

2 sin cos sin cos sin

OO O

ax xψθϕψ θθϕ





′′ ′

=− +

11 1

23 3

2 sin sin sin cos cos

OO O

ax xψθϕψ θθϕ





′′

=−

11 1

33 3

sin

OO O

ax xψθ





237

14 Dynamics of the Rigid Solid

In the system of equations (14.1.75'), (14.1.76') we take the movable frame at the point

O (maintaining thus the notations in Fig. 14.5) and we introduce the results obtained

above; the third equation (14.1.75') and the third equation (14.1.76') form a system of

two second order differential equations with the unknowns

′′

()

xxt

and

= ()tϕϕ . After integrating this system of equations, one obtains easily the other

unknowns of the problem. Obviously, in this case, as in the preceding one, certain

initial conditions of Cauchy type must be fulfilled too.

d Solid Subjected to Certain

Let us consider firstly the case of a rigid solid for which the point O is constrained to

stay on a given perfectly smooth curve C (in general, movable) of equation (14.1.72),

another point

O of which staying on a given perfectly smooth surface S (in general,

movable) of equation (14.1.70), where we replace the point O by the point

O ( = 3p ,

= 0m

). Using the axiom of liberation of constraints, the equations of motion of this

solid have the form

()

[]

1122

grad grad grad

Mfffλλ λ

′′

+× +× +× = + + +



vv R

ωωρωρ ,

(14.1.79)

()()

()

grad

OOO OOOO

Mfλ

′′ ′′

×+×++× =+ −×



vvI IMrrρω ωωω .

(14.1.79')

To determine the vector unknowns

′

and and the scalar unknowns λ,

λ and

( = 3q , 9 scalar unknowns) we have the vector equations (14.1.79), (14.1.79') and the

scalar equations (14.1.70), (14.1.72) (9 scalar equations).

Let be also the case of a rigid solid for which the points

O ,

= 1,2, 3, 4i

, are

constrained to move on a perfectly smooth surfaces (in general, movable)

S ,

= 1,2, 3, 4i

, respectively, of equations (

= 4p

, = 0m )

()( )

′′′′

123

;,,;0

iiii

OOOO

ftfxxxt, = 1,2,3, 4i .

(14.1.80)

The rigid solid remains thus with two degrees of freedom. Proceeding as in the

preceding case, we can write the equations (14.1.60), (14.1.60') in the form

()

[]

′′

+× +× +× = +

∑

vv R

grad

Mfλ



 ωωρωρ ,

(14.1.81)

()()

()

grad

OOO OO OO

Mfλ

′′ ′′

×+×++× =+ −×

∑



vvI IM rr

ρω ωωω ,

(14.1.81')

14.1.2.4 Other Cases of Motion of the Rigi

Constraint Conditions

238

MECHANICAL SYSTEMS, CLASSICAL MODELS

The vector equations (14.1.81), (14.1.81') and the scalar equations (14.1.80) (ten scalar

equations) determine thus the vector unknowns

′

and and the scalar unknowns

λ ,

= 1,2, 3, 4i ( = 4q ; ten scalar unknowns).

The general results previously obtained will be used, in what follows, to some

important cases of motion of the rigid solid; we study thus the motion of the rigid solid

about a fixed axis, as well as its plane-parallel motion.

An important particular case of that presented in Sect. 1.2.3 is that one in which

the axis is a fixed one (the two points O and

O of the rigid solid are fixed). E.g., we

mention the rigid pendulum. We will consider thus the pendulums of Borda, Kater and

Bessel, the annular pendulum of Voinaroski, the inclined pendulum of Mach and the

Weber-Gauss pendulum of torsion.

Choosing the straight line

≡

OOΔ as

Ox -axis ( =

OO l



) and noting that this

axis is fixed, it is convenient to take

′

≡OO

and

′′

≡

Ox O x ; in this case

0ωω , while =

ωω, the angular velocity vector being situated along the

′′

Ox -axis (Fig. 14.6). All the points of the rigid solid describe circular trajectories in

Fig. 14.6 Motion of a rigid solid about a fixed axis

planes normal to the

′′

Ox -axis, the centres of which are on that axis (the fixed and the

movable axoids are degenerated, coinciding with the axis). The motion has only one

degree of freedom, to which corresponds the angle

= ()tθθ (classical notation for the

14.2. Motion of a Rigid Solid about a Fixed Axis. Plane-parallel

Motion of the Rigid Solid

14.2.1 Motion of the Rigid Solid about a Fixed Axis

14.2.1.1 General Results

239

14 Dynamics of the Rigid Solid

angle of proper rotation in this motion, different of that corresponding to Euler’s

angles); we have, obviously,

=ωθ



. Taking into account the conditions

′′

vv0

, the relations (14.1.74''') are identically verified. If we put also

′

then the equations of motion (14.1.75'), (14.1.76') take the form

()

′

−+=++

211111

MRRRωρ ω ρ



()

′

+=++

122212

M RRRωρ ω ρ



′

=++

3313

0 RRR,

(14.2.1)

−=−

31 23 12

II MlRωω



+=+

23 31 11

II MlRωω



IMω



(14.2.1')

where

′

R and

are the constraint forces at the points

′

and

, respectively.

The third equation (14.2.1') can be written in the form

IMθ



(14.2.2)

too. If

()

MM tθθ



and if initial conditions of Cauchy type

()

tθθ,

() ()

===

0000

ttθωθω



(14.2.2')

are given too for the differential equation of second order (14.2.2), then we can

determine univocally the angle of proper rotation

= ()tθθ , using the theorem of

existence and uniqueness. If

, then the motion of rotation is uniform, and if

we have

0θ



(

()

,0; 0

Mtθ ) too, then the rigid solid is at rest with respect to

the fixed frame of reference. Observing that

′

and

()

′′

+=+⋅=

dd d d

RO O

WW tMtωω ,

and applying the theorem of kinetic energy in the form (14.1.66), we find again the

equation of motion (14.2.2). We mention that the pseudomoment of momentum is given

=+ +Kii

33 31 1 23 2

II Iωωω ;

we have

I ω, so that the pseudomoment of momentum is directed along the

fixed axis if and only if that axis is a principal axis of inertia.

240

MECHANICAL SYSTEMS, CLASSICAL MODELS

The first two equations (14.2.1') and then the first two equations (14.2.1) allow to

compute the constraint forces along the axes

Ox and

Ox ; we obtain

⎡

⎤⎡ ⎤

′

=−−+ −+

⎢

⎥⎢ ⎥

⎣

⎦⎣ ⎦

11223131

111

RMRM I M I

lll

ρωρω



⎡

⎤⎡ ⎤

′

=− − + + − +

⎢

⎥⎢ ⎥

⎣

⎦⎣ ⎦

22131223

111

RMRMI MI

lll

ρωρω



(14.2.3)

()

[]

=− − +

11 23 31

RMII

ωω



()

[]

=−−

12 31 23

RMII

ωω



(14.2.3')

The third equation (14.2.1) specifies only the sum

′

+=−

313 3

RR R of the other two

components of the constraint forces, the problem being thus indeterminate from this

point of view (as in the static case), due to the model of rigid solid adopted for the solid

body.

We notice that the constraint forces depend on the angular velocity and on the

angular acceleration



ω; for great values of these quantities (the square of the angular

velocity,

ω , or its non-uniformity given by



ω), e.g., for the rotation velocities of the

propellers and of the turbines, the constraint forces increase very much; the stress in the

axle increases also and it is possible to reach the state of fracture. As it was noticed by

L. Euler, this dependence disappears if

23 31

0II and ==

0ρρ , hence if the

axis of rotation is a central principal axis of inertia; it results

′

=−

RMR

′

=− −

RMR

(14.2.4)

=−

, =

(14.2.4')

corresponding to the formulae (4.2.7'') obtained in the static case (the dynamic

constraint forces coincide with the static ones). In this case, the constraint forces depend

only on the given external forces, which are equilibrating them from the statical point of

view, and are not influenced by the rotation of the rigid solid.

Putting the condition that the constraint force at the point

O be zero ( =R0

) for

any rotation of the rigid solid, we obtain

23 31

0II , ==

MM ; we get

thus the constraint forces

()

′

=− − +

11 21

RRMρω ρω



()

′

=− + −

22 12

RRMρω ρω



′

=−

RR,

(14.2.5)

the problem becoming statically determinate. Hence, for any rotation of the rigid solid,

it is sufficient only one point of support of the axis of rotation (the fixed point O) if and

only if that one is a principal axis of inertia, the given external forces having a resultant

moment with respect to the point of support, which is directed along this axis. Such an

axis is obtained, e.g., in the case in which the rigid solid is acted upon by a unique

241

14 Dynamics of the Rigid Solid

given force, situated in a plane normal to a principal axis of inertia, non-intersecting

this axis, the trace of which on the plane being a fixed point. We obtain an analogous

result if the support of the given force passes through a fixed point, the axis of rotation

(which is a principal axis of inertia) passing through the same point; in this case, we

have

M , hence =M0

too, being led to a motion of uniform rotation

(corresponding to the equation (14.2.2)), so that

′

=− −

111

RRMρω ,

′

=− −

222

RRMρω ,

′

=−

RR.

(14.2.5')

We can state

Theorem 14.2.1 If a rigid solid with a fixed point is subjected to the action of a system

of given forces equivalent to a resultant the support of which passes through this point

and if this solid has an initial uniform motion of rotation about a principal axis of

inertia which passes, as well, through the very same fixed point, then the rigid solid

continuous to have this motion indefinitely.

In this case, the axis of rotation is called permanent axis of rotation; sometimes, this

denomination (justified by the Theorem 14.1.21) is used also in the more general case

≠

M .

The supplementary condition which imposes the vanishing of the constraint force at

the point O too (

′

R0), for any rotation of the rigid solid, leads to ==

0ρρ ,

===

123

0RRR . If and only if the axis of rotation is a central principal axis of

inertia, the rigid solid being acted upon only by a couple contained in a plane normal

to this axis, then no point of support is necessary for that axis; in this case, the axis of

rotation is a free axis of rotation, and the fixed axle is not acted by a given force. If

M , hence if =M0

too, then we can state

Theorem 14.2.2 If a free rigid solid is not acted upon by any given force and has a

uniform motion of rotation about a central principal axis of inertia, then it will continue

to have this motion indefinitely, the axis remaining fixed.

In this case, the free axis of rotation is called spontaneous axis of rotation;

sometimes, this denomination (justified by the Theorem 14.2.2) is used also in the more

general case in which

≠

M . This result can be verified experimentally in a space

laboratory, in conditions of imponderability. The Theorem 14.2.2 can be considered as

a completion for the rigid solid of Newton’s “principle of inertia”, enounced for a

particle (eventually for the mass centre of the rigid solid).

We call physical (rigid, compound) pendulum a rigid solid which is rotating about a

horizontal fixed axis, being subjected only to the action of its own weight. We take the

′′′

Ox x -plane as horizontal plane, the fixed axis as

′′

Ox -axis, the

′′

Ox -axis being

along the descendent vertical. Without any loss of generality, the

Ox -axis will be

taken so as to pass through the centre of mass C, at which acts the own weight

G; the

position of the rigid solid will be thus specified by the angle of proper rotation

14.2.1.2 Physical Pendulum. Huygens’s Theorems

242

MECHANICAL SYSTEMS, CLASSICAL MODELS