Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

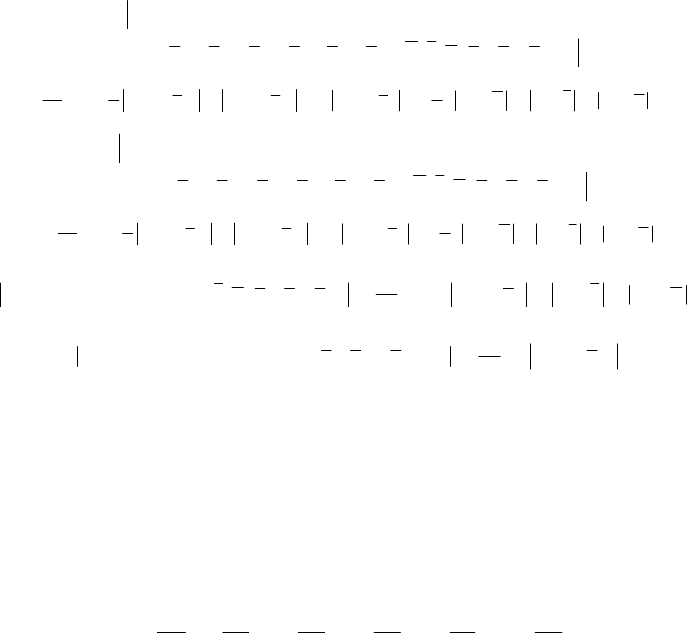
For the boundary value problem thus formulated, one can show

Theorem 14.1.12 (of existence and uniqueness; Cauchy-Lipschitz). If the functions



R ,



M ,

and

′

v , = 1, 2,3i , are continuous on the 13-dimensional interval D,

specified by

′′′

−≤≤+

00 00

Oi Oi Oi

xXxxX,

′′′

−≤≤+

00 00

Oi Oi Oi

vVv vV,

−≤≤+

00 00

ψΨ ψψΨ, −≤≤+

00 00

θΘ θθΘ,

[]

∉− +

0000

0,θΘθΘ

−≤≤+

00 00

ϕΦϕϕΦ

−≤≤+

00 00

iiiii

ωΩ ωωΩ, −≤≤+

00 00

tTttT,

00000

,,,,, const

ii i

XV TΨΘΩ , = 1,2, 3i ,

and defined on the space Cartesian product of the phase space (of canonical co-

ordinates

′′′

123

OOO

xxx, ψ, θ, ϕ,

′′′

123

,,,,,

OOO

Mv Mv Mv M M Mωωω) by the time

space (of co-ordinate t), and if Lipschitz’s conditions



()

′′′′′′

123

123123

,,,,,,,,,,,;

OOOOOO

Rx x x v v v tψθϕω ω ω



()

′′′′′′

−

123

123123

,,,,,,,,,,,;

OOOOOO

Rx x x v v v tψθϕω ω ω

()

⎧ ⎫

⎡⎤

′′ ′′

≤−+−+−+−+−+−

⎨ ⎬

⎢⎥

⎣⎦

⎩ ⎭

∑

Oj Oj Oj Oj

xx vv

λω ω ψ ψ θ θ ϕ ϕ

ττ



()

′′′′′′

123

123123

,,,,,,,,,,,;

OOOOOO

Mxxxvvv tψθϕω ω ω



()

′′′′′′

−

123

123123

,,,,,,,,,,,;

OOOOOO

Mxxxvvv tψθϕω ω ω

()

⎧ ⎫

⎡⎤

′′ ′′

≤−+−+−+−+−+−

⎨ ⎬

⎢⎥

⎣⎦

⎩ ⎭

∑

Oj Oj Oj Oj

Mxxvv

λω ω ψ ψ θ θ ϕ ϕ

ττ

()

⎛⎞

−≤−+−+−

⎜⎟

⎝⎠

∑

123 123

,, , , ,, , , ,

ii jj

ffθϕω ω ω θϕω ω ω τ ω ω θ θ ϕ ϕ

()()

′′′′ ′′′′ ′ ′

−≤−

∑

123 123

,,; ,;

Oi O O O Oi O O O Oj Oj

vxxxt vxxxt x x

where

T and L are positive (temporal and spatial, respectively) constants,

independent on

′′

Oi Oi

xv, ψ, θ, ϕ,

ω and t, while τ and λ are (temporal and spatial,

respectively) constants equal to unity, for

= 1,2, 3i , then there exists a unique solution

′′

= ()

Oi Oi

xxt,

′′

= ()

Oi Oi

vvt, ===(), (), ()tt tψψ θθ ϕϕ, = ()

tωω, = 1,2, 3i ,

of the system (14.1.53)-(14.1.53''), which satisfies the initial conditions (14.1.54) and is

defined on the interval

−≤≤+

tTttT, where

⎡

⎛⎞ ⎛⎞

⎤

⎛⎞⎛⎞⎛⎞

≤

⎜⎟⎜⎟⎜⎟

⎜⎟ ⎜⎟

⎢⎥

⎝⎠⎝⎠⎝⎠

⎣

⎝⎠ ⎝⎠

⎦

00 0

000

min , , , , , , ,

ii i

Ω

ΨΘΦ

τλλλλτ

VV V V V V

223

14 Dynamics of the Rigid Solid





⎡

⎛⎞ ⎤

⎛⎞

′

⎜⎟

⎢

⎥

⎝⎠

⎣⎝⎠

⎦

max , , , in

τλ

VD.

According to the theorem of Peano, the continuity of the functions



R ,



M ,

and

′

v on the interval D ensures the existence of the solution; for its uniqueness, the

conditions of Lipschitz must be fulfilled too. As a matter of fact, the conditions in the

Theorem 14.1.12 are sufficient conditions of existence and uniqueness, which are not

also necessary. As in the case of only one particle (see Chap. 6, Subsec. 1.2.1) or of a

discrete mechanical system (see Sect. 11.1.1.5), we can make a prolongation of

the solution for

[]

∈

,ttt, outside the interval

[]

−+

,tTtT (the time

t must

not be necessarily the initial one, but can be a time arbitrarily chosen). As well, we can

state a theorem on the continuous dependence of the solution on a parameter

(analogous to the Theorems 6.1.3 and 11.1.2), a theorem of Poincaré type on the

analytical dependence of the solution on a parameter (analogous to the Theorems 6.1.4

and 11.1.3) and a theorem on the derivability of the solutions (analogous to the

Theorems 6.1.5 and 11.1.4). Analogously, one can prove theorems concerning the

continuous dependence of the solution on the initial conditions or on several

parameters.

One can use also another representation of the motion than that based on Euler’s

angles; thus, if

()

123123

, , , , , ,,,,,,;

OOOOOO

RRxxxvvv tαααωωω

′′′′′′

= ,

()

′′′′′′

123123

,,,,,,,,,,,;

Oi Oi O O O O O O

MMxxxvvv tαααωωω ,

then we replace the subsystem (14.1.53'') by the subsystem (5.2.37'), written in the form

=−∈

ijk k

ωα

, = 1,2, 3i ,

(14.1.54)

passing to Euler’s angles by means of the relations (14.1.15), (14.1.16). The theorem of

existence and uniqueness is stated analogously for the system of equations (14.1.53),

(14.1.53'), (14.1.53'''), (14.1.54).

If, in particular, the given functions

R and

M , = 1, 2, 3i , depend on a smaller

number of variables, then the system of differential equations (14.1.53)-(14.1.53''') can

be decomposed in subsystems. Thus, if

()

′′′

123

,,,,,,,,;

OOO

RRvvv tψθϕω ω ω ,

()

′′′

123

,,,,,,,,;

Oi Oi O O O

MMvvv tψθϕω ω ω ,

then the system (14.1.53)-(14.1.53''') is decomposed in the subsystem (14.1.53''') and

the subsystem (14.1.53)-(14.1.53''), while if

()

′′′′′′

123

123123

,,,,,,,,;

OOOOOO

RRxxxvvv tωωω ,

()

′′′′′′

123

123123

,,,,,,,,;

Oi Oi O O O O O O

MMxxxvvv tωωω ,

224

MECHANICAL SYSTEMS, CLASSICAL MODELS

then this system is decomposed in the subsystem (14.1.53), (14.1.53'), (14.1.53''') and

the subsystem (14.1.53''). If

()

′′′

123

,,,,,;

OOO

RRvvv tωωω ,

()

′′′

123

,,,,,;

Oi Oi O O O

MMvvv tωωω ,

then the system (14.1.53)-(14.1.53''') is decomposed in the subsystem (14.1.53),

(14.1.53'), which specifies the velocity of the rigid solid, the subsystem (14.1.53'''),

which determines the motion of translation of the solid, and the subsystem (14.1.53''),

which puts in evidence its motion of rotation. Obviously, to each subsystem we add

initial conditions of Cauchy type in the form (14.1.54). We can state theorems of

existence and uniqueness for each of these subsystems.

We notice that one can replace the equations (14.1.53') by the equations (14.1.46'''),

passing to the principal axes of inertia.

As well, without any loss of generality, we can use the equations (14.1.47'),

(14.1.48'), (14.1.53'') in the form

′

, = 1,2, 3i ,

(14.1.55)



()

⎡

⎤

== +−

⎣

⎦

() ()

MMII

ωω ,



()

⎡

⎤

== +−

⎣

⎦

() ()

MMII

ωω ,



()

⎡

⎤

== +−

⎣

⎦

() ()

MMII

ωω

(14.1.55')

′

, = 1,2, 3i ,

(14.1.55'')

to which we associate the equations (14.1.53''); thus, the importance of the mass centre

C is put in evidence. Observing that

()

′′′′ ′ ′

123 12 3

123

,,, , , ,,,,,,;

CCC

RR vvv tρρρ ψθϕωωω ,

()

′′′′ ′ ′

123 1 2 3

123

,,, , , ,,,,,, ;

Ci Ci C C C

MM vvv tρρρ ψθϕωωω ,

()

′′′′′

123

,,;

Ci Ci

vv tρρρ , = 1, 2, 3i ,

we can adapt the Theorem 14.1.12, correspondingly. As above, if

R and

M ,

= 1,2, 3i , depend on a smaller number of variables, then the considered system of

differential equations can be decomposed, conveniently, in subsystems. Thus, if

()

′′′′ ′ ′

123

,,, , , ;

CCC

R R vvvtρρρ ,

()

123

,, , , , ;

Ci Ci

MM tψθϕω ω ω , = 1, 2, 3i ,

then the system (14.1.53''), (14.1.55)-(14.1.55'') is decomposed in the subsystem

(14.1.55), (14.1.55''), which specifies the motion of the mass centre C with respect to

225

14 Dynamics of the Rigid Solid

the inertial frame of reference

′

R (as a single particle, justifying the modelling of the

rigid solid as a particle), and the subsystem (14.1.53''), (14.1.55'), which determines the

motion of rotation of the rigid solid about the centre C (the rotation of the frame

with respect to the frame

), considered as a fixed point; this allows to study the

motion of the free rigid solid in two successive steps, representing an important

simplification of calculation. To the whole system, as well as to each subsystem, we

associate initial conditions of Cauchy type (at the moment

), of the form

()

′′

tρρ,

()

′′

Ci Ci

vt v,

()

tψψ,

()

tθθ,

()

tϕϕ,

()

tωω, = 1, 2, 3i .

(14.1.56)

For each of these subsystems one can state a theorem of existence and uniqueness. We

notice also that the subsystem (14.1.55) corresponds to the theorem of momentum with

respect to the frame

R (or to the frame

′

), while the subsystem (14.1.55')

corresponds to the theorem of moment of momentum, with respect to the same frame

R . In what follows, we suppose to be in the latter case of decomposition. We can

determine first integrals for the first subsystem, obtaining conservation theorems by

means of the considerations in Chap. 6, Subsec. 1.2.2; for the second subsystem, we use

the study contained in Chap. 15, §1 for the rigid solid with a fixed point.

The equations of motion used above have been written with respect to the non-

inertial frame of reference

R. Starting from the theorem of torsor written for a free

rigid solid, by means of the relations (14.1.44'), and observing that

′

′′′′

=+×KKrH

, we can write these equations with respect to the inertial frame

′

in the form

′

∂

⎛⎞

⎜⎟

′

∂

⎝⎠

′

′′

∂∂

⎡⎤

′

+∈ =

⎢⎥

′′

∂∂

⎣⎦

ijk Oj

, = 1,2, 3i

(14.1.57)

too. Passing from the frame

′

R to the frame R, we find again the above results.

=R0 on an interval of time

[]

,tt ,

being the initial moment, then the mass

centre C has a uniform and rectilinear motion, so that

′′

()

Ci Ci

vt v

, while

()

′′ ′

=−+

()

tvttρρ, = 1,2, 3i , for

[]

∈

,ttt; in particular, if

′

v ,

= 1, 2, 3i

, hence if the mass centre C is at rest with respect to the inertial frame of

reference

′

at a given moment t (e.g., at the initial moment), then this point remains

at rest in the whole interval

[]

,tt . If =M0

in the time interval

[]

,tt , then the

solution of the subsystem of equations (14.1.55') corresponds to an Euler-Poinsot

motion of the free rigid solid (particular case of rotation of a rigid solid about the mass

centre C , considered to be fixed; see Sect. 15.1.2), which depends of the initial

condition

()

tωω; if, in particular, =

ω , = 1, 2, 3i , hence if the free rigid

14.1.1.9 State of Rest

226

MECHANICAL SYSTEMS, CLASSICAL MODELS

solid (the frame

R too) does not rotate with respect to the frame R at a moment t

(e.g., the initial moment), it will not rotate in the whole interval of time

[]

,tt . We

can thus state

Theorem 14.1.13 A free rigid solid subjected to the action of a system of given

external forces of null torsor has an inertial motion (a uniform rectilinear motion of

translation, with respect to an inertial frame of reference, associated to an Euler-

Poinsot motion with respect to the mass centre, considered as a fixed point).

This result can be considered also as a principle, generalizing the principle of inertia

(from a free particle to a free rigid solid).

If, in particular, the kinematic torsor

{

}

′

ω vanishes, then we can state that the

free rigid solid subjected to the action of a given system of external forces of null torsor

remains at rest (in equilibrium) with respect to an inertial frame of reference if that

state has been its initial one; we find thus again the Theorem 4.2.1, where we have a

priori neglected the possibility of existence of homogeneous initial conditions. As well,

the free rigid solid subjected to the action of two given external forces, of equal

magnitude and contrary directions, having the same support (of null torsor), conserves

its initial state of rest or motion with respect to an inertial frame of reference; we find

thus again the modelling as sliding vectors of the forces which act upon a rigid solid

(see Chap. 2, Subsec. 2.2.2). We mention also (what was stated before too) that two

systems of given external forces having the same torsor (systems of equivalent forces)

have the same effect (motion or rest), with respect to an inertial frame of reference,

upon a free rigid solid (we apply the Theorem 14.1.13, the difference of the initial

conditions vanishing); e.g., the field of gravity forces which act upon a free rigid solid

can be replaced by a resultant (the own weight of the solid), applied at the mass centre

The Theorem 4.1.8 allows to state

Theorem 14.1.14 (theorem of virtual work) The necessary and sufficient condition of

equilibrium of a free rigid solid, acted upon by a system of given external forces, is

given by the vanishing of the virtual work of these forces for any system of virtual

displacements of the respective solid.

Using the form (4.1.58') of this theorem, which implies the introduction of virtual

velocities with respect to the frame of reference

′

R , of the form

∗∗ ∗

=+×vv r

ω ,

= 1, 2, 3i

(14.1.58)

corresponding to Euler’s formula (5.2.3), we can write

()

∗∗∗

⋅= ⋅ +×

∑∑

Fv F v r

ii i i

∗∗ ∗∗

=⋅ +⋅ ×=⋅+⋅ =

∑∑

vF rFvR M

iii

OOO

ωω

14.1.1.10 Principle of Virtual Work

227

14 Dynamics of the Rigid Solid

Taking into account that the virtual quantities

∗

and

∗

ω are arbitrary, it results that

the torsor of the external forces at the pole O (in this case, the frame

R is inertial too)

must be equal to zero for equilibrium, hence the same result as above. Obviously, as in

the case considered in Chap. 4, Subsec. 1.2.3, we can start from the Theorem 14.1.14

considered as a principle, finding again the results from which we started in the state of

rest problem.

In the dynamic case, the Theorem 11.1.28 allows to state

Theorem 14.1.15 (theorem of virtual work; d’Alembert-Lagrange) The motion of a

free rigid solid takes place so that the virtual work of the lost volume forces of

d’Alembert which act upon it vanishes for any system of virtual displacements of the

respective solid.

We notice that, in this case, we have to do with a continuous mechanical system, so

that we can no more use Newton’s equation (hence the lost forces of d’Alembert) in the

classical form, being necessary to introduce the lost volume forces of d’Alembert.

Using the virtual velocities

∗∗ ∗

=+×vv r

ω ,

(14.1.58')

we can write

∗

′

⎡⎤

−⋅=

⎢⎥

⎣⎦

∫∫∫

Fr v

() d 0

μ ,

(14.1.59)

so that

()

∗∗

′

⎡⎤

−⋅+×

⎢⎥

⎣⎦

∫∫∫

Fr v r

() d

μ ω

∗∗

′′

⎡⎤ ⎡⎤

=⋅ − +⋅ ×− =

⎢⎥ ⎢⎥

⎣⎦ ⎣⎦

∫∫∫ ∫∫∫

vFr rFr

() d () d 0

μμω ,

wherefrom

′

⎡⎤

−=

⎢⎥

⎣⎦

∫∫∫

() d 0

μ ,

′

⎡⎤

×− =

⎢⎥

⎣⎦

∫∫∫

rF r

() d 0

μ ,

being thus led to the theorem of torsor for a free rigid solid. Obviously, the Theorem

14.1.15 can be enounced also in the form of a principle.

If the rigid solid is acted upon by the given external forces

, = 1,2,...,in, we can

write the theorem of virtual velocities in the form

∗∗

′

⎡⎤

⋅+ − ⋅ =

⎢⎥

⎣⎦

∑

∫∫∫

Fv r v

() d 0

(14.1.59')

The Theorem 14.1.15 can be stated correspondingly.

228

MECHANICAL SYSTEMS, CLASSICAL MODELS

In what follows, after some general results, we study various particular cases of

constraints in which parts of a rigid solid have given motions; we consider thus several

general classes of constraints to which the rigid solid can be subjected, establishing the

corresponding equations of motion.

If a rigid solid is subjected to constraints which may be holonomic or non-

holonomic, scleronomic or rheonomous, bilateral or unilateral, ideal or with friction,

then we must introduce in the system of equations of motion – using the axiom of

liberation of constraints – also the torsor

{

}

RM,

of the system of constraint forces at

the pole O of the non-inertial frame of reference

R, rigidly linked to the solid. We

replace thus the equations (14.1.51), (14.1.51') by the equations

()

[]

′′

+× +× +× = +

vv RR



ωωρωρ ,

(14.1.60)

()()

′′

×+×++× =+

vvI IMM

OOO OO



ρω ωωω ,

(14.1.60')

with respect to the frame

R. If ≡OC, these equations become

()

′′′

=+×=+

avvRR

CCC



ω ,

(14.1.61)

()

+× = +IIMM

CCC



ωω ω .

(14.1.62)

With respect to the central principal axes of inertia, we have

′

Ma R R

= 1, 2, 3i

(14.1.61')

()

+− =+

() () ()

123

132

CCC

III MMωωω



()

+− =+

() () ()

231

213

CCC

III MMωωω



()

+− =+

() () ()

312

321

CCC

III MMωωω



(14.1.62')

We add to these equations initial conditions of Cauchy type too, e.g., of the form

(14.1.56).

As a matter of fact, the equations (14.1.60), (14.1.61) correspond to the equations

(14.1.38), (14.1.39), written in the form

′

(14.1.63)

′

aRR

M .

(14.1.63')

We can thus state:

Theorem 14.1.16 (theorem of momentum) The derivative with respect to time of the

momentum of a rigid solid subjected to constraints, in an inertial frame of reference, is

14.1.2 Motion of the Rigid Solid Subjected to Constraints

14.1.2.1 General Results

229

14 Dynamics of the Rigid Solid

equal to the resultant of the given and constraint external forces which act upon this

solid.

Theorem 14.1.16' (theorem of motion of the mass centre) The centre of mass of a rigid

solid subjected to constraints moves, with respect to an inertial frame of reference, as a

free particle at which would be concentrated the whole mass of the solid and which

would be acted upon by the resultant of the given and constraint external forces.

As well, the equations (14.1.60'), (14.1.62) correspond to the equations (14.1.40),

(14.1.41'), written in the form

()

′

×+=+

aMM

ρ ,

(14.1.64)

(14.1.64')

We thus state:

Theorem 14.1.17 (theorem of moment of momentum) The derivative with respect to

time of the pseudomoment of momentum of a rigid solid subjected to constraints, with

respect to an arbitrary pole O, rigidly linked to the solid, in an inertial frame of

reference, is equal to the resultant moment of the given and constraint external forces

which act upon this solid, with respect to the same pole, from which one subtracts the

dynamic moment, in the inertial frame, of the considered pole, translated at the centre

of mass of the rigid solid, at which one assumes that would be concentrated the whole

mass of the solid, with respect to the pole O.

Theorem 14.1.17' The derivative with respect to time of the pseudomoment of

momentum of a rigid solid subjected to constraints, with respect to the mass centre, in

an inertial frame of reference, is equal to the resultant moment of the given and

constraint external forces which act upon this solid, with respect to the same centre.

In what concerns the work, the formula (14.1.37) takes the form

() ()

′′ ′

+=+⋅++⋅

RR r M Mdd d d

ROO

WW tω

(14.1.65)

and the formula (14.1.37') becomes

()()

′′ ′

+=+⋅+ + ⋅

RRv M M

ROO

PP ω,

(14.1.65')

so that we can state

Theorem 14.1.18 The power of the given and constraint external forces which act

upon a rigid solid subjected to constraints, with respect to a given frame of reference, is

equal to the power of the torsor of the given and constraint external forces, at an

arbitrary pole, rigidly linked to the solid, in the same frame.

The formula (14.1.12) becomes

()()

′

=+⋅+ + ⋅

RRv M M

(14.1.66)

so that we state

230

MECHANICAL SYSTEMS, CLASSICAL MODELS

Theorem 14.1.19 (theorem of kinetic energy) The derivative with respect to time of the

kinetic energy of a rigid solid subjected to constraints, in an inertial frame of reference,

is equal to the power of the torsor of the given and constraint external forces, at an

arbitrary pole, rigidly linked to the solid, in the same frame.

Obviously, in this case too, the theorem of kinetic energy is a linear consequence of

the theorems of momentum and moment of momentum.

In general, the rigid solid may be subjected to p holonomic constraints of the form

(3.2.8), specified by the relations

()( )

′′′′

123

,,,; , , ,,,; 0

lO l O O O

ftfxxxtψθϕ ψθϕ , = 1,2,...,lp,

(14.1.67)

and to m non-holonomic constraints of the form (3.2.13), given by the relations

′′

⋅+⋅+= + +=

v 0

k O k k kj Oj kj k

vγα βωγαβω , = 1,2,...,km.

(14.1.67')

We have assumed that these constraints are bilateral; the unilateral constraints can be

analogously introduced. Obviously, we can express the components

ω as functions of

the angular velocities



, θ



and ϕ



in the constraint relations (14.1.67'). We notice that

the relations (14.1.67) can be written in the form

∂∂∂

′

=⋅++++=

∂∂∂

grad 0

llll

lO l

ffff

ψθϕ



, = 1,2,...,lp

(14.1.67'')

too, wherefrom

∂

⎛⎞

⎜⎟

′′

∂∂

⎝⎠

Oj Oj

vt x

, = 1, 2, 3j ,

∂

⎛⎞

⎜⎟

∂

∂⎝ ⎠

t ψ



∂

⎛⎞

⎜⎟

∂

⎝⎠

∂



∂

⎛⎞

⎜⎟

∂∂

⎝⎠

ϕϕ



Taking into account (14.1.15), we can also write

sin

grad cos cos

sin

ll l

ff f

θϕω

ψϕ θ θ

∂∂ ∂

⎡

⎛⎞ ⎤

′

⋅+ − +

⎜⎟

⎢

⎥

∂∂ ∂

⎣⎝ ⎠

⎦

cos

cos sin 0

sin

ll l l

ff f f

θϕωω

ψϕ θ θ ϕ

∂∂ ∂ ∂

⎡⎛ ⎞ ⎤

+− − + +=

⎜⎟

⎢⎥

∂∂ ∂ ∂

⎣

⎝⎠

⎦



= 1,2,...,lp

as well as

∂

sin

ωθ



∂

cos

sin

ωθ



∂



∂

cos



∂

=−

∂

sin



∂



231

14 Dynamics of the Rigid Solid

sin cot

ϕθ

∂

=−

∂



cos cot

ϕθ

∂

=−

∂



∂



Finally, we get

∂∂

⎛⎞ ⎛⎞

′

⎜⎟ ⎜⎟

′

∂∂

⎝⎠ ⎝⎠

Oj l

vt t



′

=⋅+⋅+=

grad grad 0



ω , = 1,2,...,lp.

(14.1.67''')

These results have a general character and allow to determine the constraint forces in

any particular case.

We notice that one must have

+<6pm , otherwise the rigid solid remains at rest;

we assume, obviously, that the constraint relations are independent. On the other hand,

the constraint forces involve q unknown scalars; if

=+qpm, then the problem of the

rigid solid motion is determined. In general, the equations of motion and the constraint

relations are not independent, so that the kinetostatic problem can be separated in two

problems only in particular cases: the kinetic problem (determination of the kinematic

parameters

′

and of the motion) and the static problem (determination of the torsor

{

}

RM,

of the constraint forces).

We mention that the Theorems 14.1.14 and 14.1.15 concerning the virtual work are

completed in the form:

Theorem 14.1.20 (theorem of virtual work) The necessary and sufficient condition of

equilibrium of a rigid solid subjected to ideal constraints and acted upon by a system of

given external forces consists in equating to zero the virtual work of these forces for

any system of virtual displacements of the respective solid.

Theorem 14.1.21 (theorem of virtual work; d’Alembert-Lagrange) The motion of a

rigid solid subjected to ideal constraints takes place so that the virtual work of the lost

forces of d’Alembert, which act upon this solid, vanishes for any system of virtual

displacements of the respective solid.

Let us suppose that the point O rigidly linked to the solid has a known motion, given

by the equation

′′

rr()

t ,

(14.1.68)

with respect to the inertial frame of reference

′

; obviously, in this case, we know the

velocity

′′

vv()

t and the acceleration

′′

aa()

t too. Eliminating the constraint

by introducing the constraint force

R and using the system of equations (14.1.60),

(14.1.60'), we can write the equations of motion of the rigid solid in the form

()

[]

′

×+× × = − +

RaR



ωρ ω ωρ

(14.1.69)

14.1.2.2 Rigid Solid a Point of Which has an Imposed Motion

232

MECHANICAL SYSTEMS, CLASSICAL MODELS