Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

Chapter 14

Dynamics of the Rigid Solid

If for any input (for any system of external forces) or for any interactions (system of

internal forces) all the pairs of points (particles) of a mechanical system remain at a

mutual invariant distance in time, then we have to do with a non-deformable

mechanical system; in case of a continuous non-deformable medium we use the

denomination of rigid solid. This notion represents an idealization of physical reality,

because any body subjected to the action of forces is deformed; but often these

deformations are very small with respect to the dimensions of the body. Thus, the rigid

solid (body) represents a mathematical model of the bodies the deformation of which

can be neglected in a first approximation. Sometimes, in case of special problems

concerning the rigid solids, there can appear contradictions and it is necessary to

complete the mathematical model, assuming that the mechanical system is no more

rigid (partially or in its totality); this happens, for instance, in the calculation of the

constraint forces which appear in case of hyperstatic mechanical systems, in some cases

of friction or in other problems concerning the collision of bodies. The problems put in

mechanics of rigid solids form what is called stereomechanics.

We present firstly the problems concerning the free or constrained rigid solid;

starting from these results, we consider then the motion of the rigid solid about a fixed

axis, as well as the plane-parallel motion of it.

14.1 Motion of a Free or Constrained Rigid Solid

In what follows, we will give results and will establish general theorems for the motion

of the free or constrained rigid solid; the results thus obtained will be applied to various

particular cases.

14.1.1 Motion of the Free Rigid Solid

After some preliminary considerations concerning the representation of the rigid

displacement of a solid, the geometric and mechanical quantities which appear in case

of a free rigid solid are specified; the corresponding general theorems are then stated, in

these conditions.

14.1.1.1 Finite Rototranslations

We have seen that a rigid solid

S is characterized by the relation

P.P. Teodorescu, Mechanical Systems, Classical Models,

193

MECHANICAL SYSTEMS, CLASSICAL MODELS

194

const

ij j i

′′

=−=





(14.1.1)

where

′

and

′

are the position vectors of two arbitrary points,

P and

P ,

respectively, with respect to the inertial frame

′

. We have shown in Chap. 3,

Sect. 2.2.3 that a free rigid solid has six degrees of freedom, so that its position with

respect to a fixed frame of reference can be represented by six parameters, which can

be, e.g.: the co-ordinates

′

of a point O of the rigid solid and Euler’s

angles (the angle of precession ψ,

02ψπ≤< , the angle of nutation θ,

0 θπ≤≤

and the angle of proper rotation ϕ,

02ϕπ≤<

), which specify the rotation of the

rigid body with respect to the point O (the orientation of a non-inertial frame

R rigidly

linked to the solid and with the pole at O, with respect to a non-inertial frame

R , with

the pole at O and with the axes parallel to the axes of an inertial frame

′

) (Fig. 14.1).

Let be a square matrix

M with complex elements. The matrix

=MM, where

M is the transpose of the matrix M (obtained by replacing the lines by the columns),

while

M is the conjugate matrix of the matrix M (obtained by replacing its elements

by the corresponding complex conjugate elements), is called the adjoint matrix of the

matrix

M. If

=MM

, then the matrix M is real (all its elements are real), while if

=−MM, then the matrix M is purely imaginary. A square matrix S is called

Fig. 14.1 The rigid solid in an inertial frame of reference R

and in non-inertial ones

R and R

′

195

symmetric or antisymmetric (skew-symmetric) as we have

=SS

=−SS

respectively. A square matrix

H is called Hermitian (self-adjoint) or antiHermitian if

=HH or

=−HH, respectively; we notice that a real and symmetric matrix is

Hermitian. If a square matrix

O satisfies the relation

T1−

=OO, where

1−

O is the

inverse of the matrix

O (

11−−

==OO O O E , E being the unit matrix), that is

==OO O O E , then O is called orthogonal complex matrix, while if a square

matrix

U satisfies the relation

1+−

=UU

(

==UU U U E ), then it is called unitary

matrix. If

1+−

=RR

and

=RR

(the square matrix R is unitary and real), then

T +−

===RRRR

, that is

T1−

=RR; in this case, the matrix R is called

orthogonal real matrix (or only orthogonal). The sum of the elements of the principal

diagonal of a square matrix

M represents the trace of the matrix (denoted by tr M),

being an invariant to a linear transformation of the matrix elements.

The matrix specified by (3.2.11''') allows to pass from the frame

(or

from the frame

′

) to the frame R by the transformation relation (3.2.11'') of the

form

′

=iiα

; in other words, the transformation matrix may be conceived as an

operator which, acting on the frame

R , transforms that one in the frame R. If the

matrix operates on the components of a vector

r in the frame

, then we obtain

the components of the vector

=rr in the frame R (the vector does not change); we

can, as well, consider the relation

∗

=rrα , which transforms a vector r in a vector

∗

in the same frame R. In the first case, the matrix corresponds to a counterclockwise

rotation, while in the second case it corresponds to a clockwise one. The matrix is an

orthogonal one, the trace of which does not vanish, in general.

Because we can determine, at any moment, the position of the rigid solid by the

position of the frame

R with respect to the frame R , hence by the parameters which

specify this position, the transformation matrix will be of the form

(t ); if at the

initial moment

tt= we have ≡RR, then it results

()t = Eα , coinciding with

the unit matrix. The motion being continuous, the matrix

(t ) must be a continuous

function of time and we can state that it is obtained by continuity from the identical

transformation. Taking into account the rigidity condition (14.1.1), it results that the

matrix is orthogonal.

We will assume now that the pole O, common to the frames

R and R is fixed. If

the motion of the frame

R about O is a motion of rotation, then there exists a direction

which corresponds to the axis of rotation and which is not affected by the operator , a

vector along this direction having the same components in the two frames. To put in

evidence the existence of such a direction we will show that there exists a vector

which has the property

r = r. On the other hand, the equation =rrλα , λ scalar, has

a solution for the eigenvalues λ of the matrix ; we will try to show that between these

eigenvalues is also the eigenvalue

= 1λ . The equation ()λ−=E0

leads to the

characteristic equation

[]

det 0λ−=Eα , which gives the eigenvalues

123

,,λλλ

(see

α = ΦΘΨ

α = α

14 Dynamics of the Rigid Solid

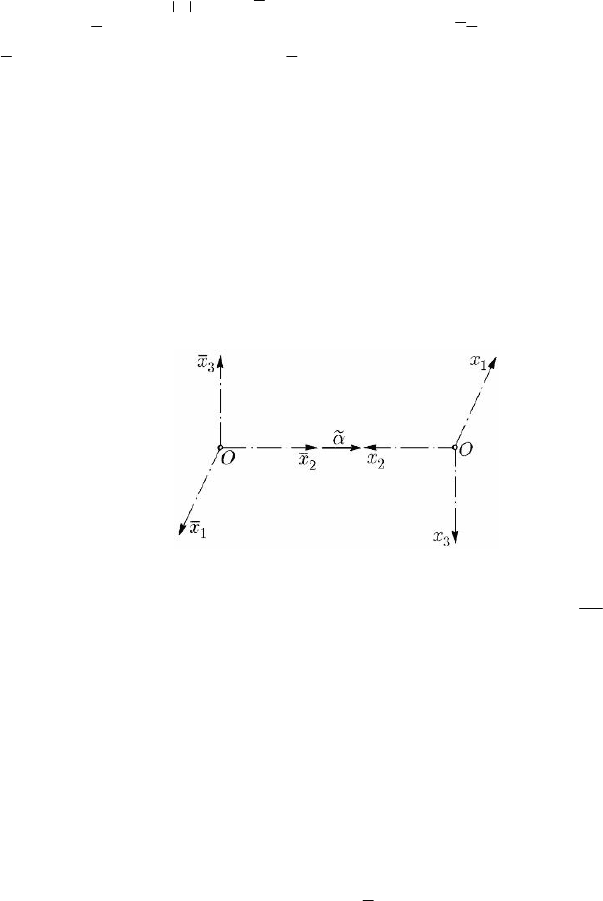
Chap. 3, Sect. 1.2.3 too). Due to the orthogonality of the matrix , the modulus of a

vector

r remains invariant by the mentioned transformation. The characteristic equation

(an algebraic equation of third degree with real coefficients) has at least a real root and

can have also complex solutions, the corresponding eigenvectors being, in this case,

complex (they do not exist in the real physical space). The modulus of such a vector is,

in the general case,

=⋅rrr, where we have put in evidence the conjugate

eigenvector

; by transformation, one obtains ()( )λλ⋅rr, so that we must have

1λλ = (if λ is an eigenvalue, then λ is an eigenvalue too). The real root can be only

λ = ±1. We notice that

123

det λλλ=α and can be equal to ±1. Because one cannot

pass by a jump (the motion is continuous) from

det ( ) det 1t ==Eα (corresponding

to a proper rotation) to

det 1=−α (corresponding to an improper rotation), it results

that one can have only

det ( ) 1t =α . A transformation matrix of the form



10 0

010

00 1

⎡⎤

−

⎢⎥

≡− =−

⎢⎥

−

⎢⎥

⎣⎦

Eα



det 1=−α ,

would correspond to an inversion (reflection) of the axes of the frame

R , but there

does not exist any rigid motion which could transform a right-handed frame of

reference into a left-handed one or conversely (to do this, one must pass by a four-

dimensional space) (Fig. 14.2); hence, an inversion can never correspond to a real

displacement of a rigid solid. We obtain the same conclusion for any transformation

matrix for which

det 1=−α , including thus the inversion operation, because such a

matrix can be written in the form



=ααα,

det 1=α

. Obviously, on this way we

obtain the same conclusion as above. The three eigenvalues of the matrix cannot be

distinct, if they are real, because

λ =± , j = 1,2,3. If two of the eigenvalues are

equal, then they cannot be real and equal to −1 (the third of the eigenvalues must be

equal to 1, to can have

123

1λλλ = ); one obtains the same conclusion if two of the

eigenvalues are complex conjugate, because

1λλ = . The trivial case in which all three

roots are real (

123

1λλλ===) corresponds to the identical transformation. Hence,

one can state that, excluding the above mentioned trivial case, to any rigid motion

Fig. 14.2 Impossibility to transform a right-handed frame of reference in a left-handed one

196

MECHANICAL SYSTEMS, CLASSICAL MODELS

corresponds only a single eigenvalue equal to 1. For the general displacement of the

rigid solid by which that one passes from a position to another one, with respect to a

given frame of reference, we can state

Theorem 14.1.1 (L. Euler) The general displacement of a rigid solid with a fixed point

is a finite rotation about an axis which passes through this point and is uniquely

determined.

We can always transform the matrix so as to obtain a new matrix

∗

leading to a

frame

R (

∗

′

iiα

), with the axis

Ox along the rotation axis; in this case

cos sin 0

sin cos 0

001

χχ

∗

⎡

⎤

⎢

⎥

=−

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

(14.1.2)

where χ is the rotation angle. We notice that

tr 1 2 cos χ

∗

=+α ; knowing that the

trace of the matrix is invariant with respect to the transformation thus effected, we have

also

tr 1 2 cosχ=+α . In case of the matrix of the form (3.2.11'''), we can express

the angle χ as a function of the Euler angles by the relation

()

cos cos cos sin

θθ

χψϕ=+−

(14.1.3)

If we suppress the link imposed to the rigid solid (the fixed point) and if we

introduce the three degrees of freedom corresponding to the translation of the origin O

of the frames

R and R, then we can state

Theorem 14.1.2 (Chasles) The general displacement of a free rigid solid is a finite

rototranslation.

ernions. Stereographic Parameters

Besides the representation of the rotation of the rigid solid by means of Euler’s

angles, one can imagine other representations too, useful in various cases. Thus, the

finite rotation of angle χ about an axis of unit vector

u, which passes through the pole

O, can be characterized by the set

{

}

{

}

,2 , 2nnχπ χπ+=−−+uu, n ∈ Z; but this

representation is multiform. We can reduce this multiplicity by introducing a vector

of components λ, μ, ν, and a scalar ρ in the form

=Vusin

, = cos

2222

1λμνρ+++=.

(14.1.4)

We see easily that the parameters

λ, μ, ν, ρ which satisfy this relation determine a

unique rotation; but to a given rotation correspond the parameters −

λ, −μ, −ν, −ρ too,

14.1.1.2 Eulerian Parameters. Quat

197

14 Dynamics of the Rigid Solid

hence two sets of parameters. Hence, the parameters

λ, μ, ν, ρ, called Eulerian

parameters, can describe – analogously – the rotation of the rigid solid; if we consider

these parameters as Cartesian co-ordinates of a point in the

E -space, then we can

state: (i) any point of the hypersphere (14.1.4) can specify the actual (final)

configuration (position) of the rigid solid; (ii) any actual configuration of the rigid solid

determines two diametrical opposite points on the hypersphere; (iii) there exists a

straight lines passing through the origin of the space

E .

Let be P

(r ) and ()P

∗

r the initial and the actual positions of a point of the rigid

solid, respectively, which are rotated by an angle

χ about an axis which passes through

the pole O and is specified by the unit vector

u (or by the vector V) and let be Q their

common projection on this axis; at the point Q we consider a right-handed orthogonal

frame, determined by the vectors

QP =





p , q, 1=q , and V (Fig. 14.3). We can write

cos sinOQ QP OQ χχ

∗∗

=+ =+ +









rpq

;

but

OQ=−





Vp Vp

so that

()

22 2

sin

cos 1 cos 2 2

OQ V V OQ

χχ ρ ρ

∗

=+−+ ×=−+ +×





rr Vr r Vr

Because

()VOQ=⋅





VrV

, we have, finally,

one-to-one correspondence between the actual configuration of the rigid solid and the

Fig. 14.3 Eulerian parameters

198

MECHANICAL SYSTEMS, CLASSICAL MODELS

()

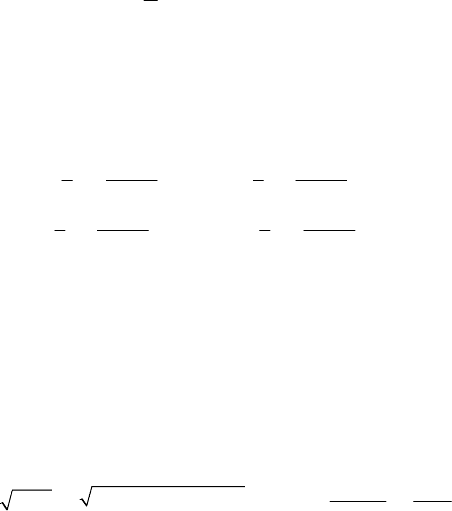
22Vρρ

∗

=− + ⋅ + ×rrVrVVr;

(14.1.5)

projecting on the axes of the frame

R, we obtain

ij j

xxα

∗

= ,

()

ij ij i j

kk ijk k

VV VV Vαρ δ ρ=− + −∈,

(14.1.5')

so that the transformation matrix is

() ()

2222

ρλμν λμνρ νλμρ

λμ νρ ρ μ ν λ μν λρ

νλ μρ μν λρ ρ ν λ μ

⎡⎤

+−− − +

⎢⎥

=+ +−− −

⎢⎥

−++−−

⎢⎥

⎣⎦

(14.1.6)

++=

222 2

sin

λμν ,

2222

1λμνρ+++=,

(14.1.6')

corresponding to Olinde Rodrigues’s formulae.

Obviously, this matrix remains invariant if one changes the signs of Euler’s

parameters. By comparison with the matrix (3.2.11''') which depends on Euler’s angles,

we find easily (we consider one of the two determinations)

−

= sin cos

ψϕ

−

= sin sin

ψϕ

= cos sin

ψϕ

=−cos cos

ψϕ

(14.1.6'')

A quaternion q is defined in the form

qijkabc d=++ +, a,b,c,d ∈ R, where

i,j,k are quaternion units, which satisfy the relations

22 2

ijk 1== =−,

jk kj i=− = , ki ik j=− = , ij ji k=− = . The vector part Vq, the scalar part Sq, the

conjugate quaternion Kq, the norm N q and the reciprocal quaternion

−

are defined

by the relations

qijkabc=++V

qSd=

qqqS=+V

qqqKS=− +V

222 2

qqqNKabcd==+++

()

−

The vector part

Vq can be considered as a usual vector; thus, if q0S = , then the

quaternion q degenerates, becoming a vector. A quaternion q determines a number

0h > , a unit vector p and an angle χ, 02χπ≤< , by the relation

() ()

[]

qcos/2psin/2h χχ=+; in this case,

qNh=

, while

() ()

[]

q cos /2 psin /2h χχ

−−

=−.

Let be the quaternion

qijkλμν ρ=++ +,

2222

1λμνρ+++=, hence with

q1N = ; we have

qijkλμν ρ

−

=− − − + . We introduce also the degenerate

199

14 Dynamics of the Rigid Solid

quaternions

12 3

rijkxx x=++,

123

rijkxxx

∗∗∗ ∗

=++ with rr0SS

∗

==. The

relation

rqrq

∗−

= defines a transformation which represents a rotation of angle χ

about the axis p. Passing to a matric notation, we find again the matrix (14.1.6),

λ, μ, ν

and

ρ being thus Eulerian parameters; we obtain, in a quaternion notation, a new form

of the respective representation. Observing that

1h = , it results

qpsin

=V ,

()

=++=V

222 2

qsin

λμν

, ==qcos

;

(14.1.7)

hence, the vector

Vq is the vector V (along the rotation axis), the angle χ of the

quaternion being the rotation angle.

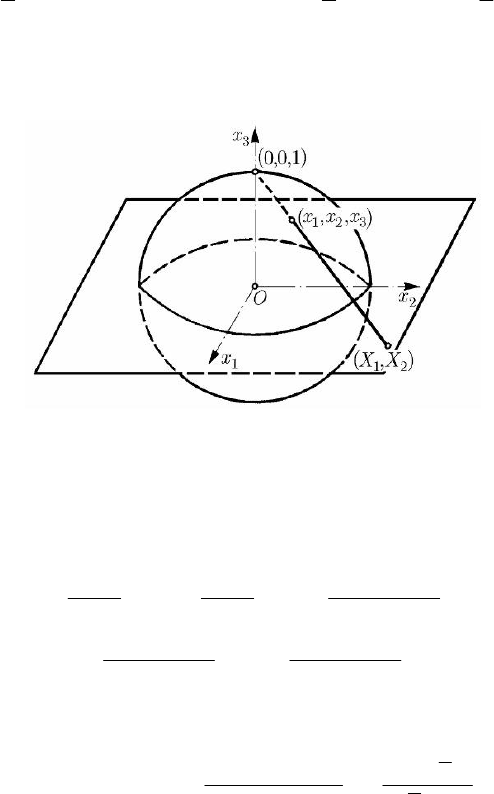
Projecting the unit sphere

222

123

1xxx++= from the point (0,0,1) on the plane

0x = , one obtains a stereographic projection. Let

()

,XX be thus the projection

of the point

123

(,, )xxx (Fig. 14.4); we will have

−

, =

−

+−

as well as

()

++= =

222

123

ddd4 4

xxx

Fig. 14.4 Stereographic projection

200

MECHANICAL SYSTEMS, CLASSICAL MODELS

where we have denoted

iZX X=+, Z being the complex conjugate. Any

transformation

∗

→

induces a transformation

()

123 123

(,, ) ,,xxx xxx

∗∗∗

→ of the

unit sphere in itself, which will be rigid if the sum

xx is conserved, hence if

()

∗

dd dd

ZZ ZZ

One can show that this condition is satisfied by the transformations

∗

−+

pZ q

qZ p

, 1pp qq+=,

(14.1.8)

where the stereographic parameters p and q are complex numbers to which correspond

three degrees of freedom. Observing that

()()

∗

∗∗

∗

+= = + − + −

12 12 12 3

iii2

xx pxxqxx pqx

()()

12 12 12 3

ii i2xxpxx qxx pqx

∗∗

−= − − + − ,

()()

()

∗

−

==++−+−

312123

x pqx x pqx x pp qqx

we find the transformation matrix

()()

()

()()

()

⎡

⎤

+−− −+− − +

⎢

⎥

⎢

⎥

=−+− +++ −

⎢

⎥

⎢

⎥

+−−

⎢

⎥

⎢

⎥

⎣

⎦

22 22

22 2 2

2222

p p q q p p q q pq pq

pq pq pq pq pp qq

(14.1.9)

hence a new representation of the motion of rotation (not only of the rigid motion of the

unit sphere about its centre) by means of the stereographic parameters.

Comparing the expressions (14.1.6) and (14.1.9) of the matrix , taking into account

(14.1.6'') and by a choice of sign, we find the connection between the stereographic

parameters, the Eulerian parameters and Euler’s angles in the form

()

−+

=+ =−

icose

ψϕ

ρν

()

−

=− + =

iisine

ψϕ

μλ

(14.1.10)

201

14 Dynamics of the Rigid Solid

Starting from the above results, we define the complex numbers

()

=− =− + =

icose

ψϕ

αρν

()

−−

=− = + =

iisine

ψϕ

βμλ

(14.1.11)

()

−

==−+ =

i/2

iisine

ψϕ

γμλ

()

−+

=− =− − =

icose

ψϕ

δρν

(14.1.11')

which satisfy the condition of unimodularity, being connected by the relations

γβ=−

δα= ,

αβ

αδ βγ αα β β

γδ

=−= + =

(14.1.11'')

corresponding to the relation (14.1.8) between the stereographic parameters. These

numbers are the Cayley-Klein parameters of the motion of rotation and constitute a new

representation of it. The corresponding transformation matrix will be

()()

()

⎡⎤

−−+ +−− −

⎢⎥

=−+− +++−+

⎢⎥

−++

⎢⎥

⎣⎦

2222 2222

αβγδ γδαβ γδαβ

αβγδ αβγδ αβγδ

βδ αγ αγ βδ αδ βγ

(14.1.12)

The above given parametric representations correspond to the group of proper

rotations

(3)O

; but they can be put in connection with the two-dimensional special

unitary group

(2)SU , homomorphic with the group (3)O

too. Thus, the Cayley-

Klein representation is characterized by the matrix

αβ

γδ

βα

⎡

⎤

⎡⎤

≡=

⎢

⎥

⎢⎥

−

⎢

⎥

⎣⎦

⎣

⎦

Q ,

1αβ+=,

(14.1.13)

where

α and β are the complex Cayley-Klein parameters, while λ, μ, ν, ρ,

2222

1λμνρ+++=, specified by the relations (14.1.11), (14.1.11'), are the real

Cayley-Klein parameters of the

(2)SU group (they coincide with Euler’s parameters).

We can choose as independent parameters the real numbers

λ, μ, ν and sgn /ρρρ= ,

the magnitude of

ρ being given by the last relation (14.1.6'). The elements of the matrix

Q being defined by (14.1.11), (14.1.11'), it results 1α ≤ , 1β ≤ , so that we can

14.1.1.3 The Cayley-Klein Parameters. Pauli’s Matrices

202

MECHANICAL SYSTEMS, CLASSICAL MODELS