Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

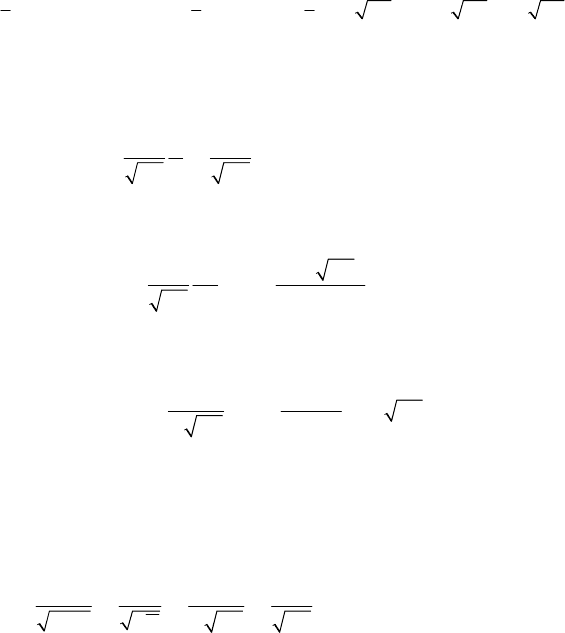
We can write the relations (11.2.29), (11.2.29') too, introducing the axial moment of

inertia with respect to the instantaneous axis of rotation

Δ; thus, the axial moment of

inertia plays the rôle of a mass in the instantaneous motion of rotation. Noting that

is the vector homologous to d , we may write

[]

⋅= ⋅×× = ×⋅ ×

∫∫∫ ∫∫∫

Krrrrrrd()d()d ()()(d)d

VVμμωωω ωω

[]

=⋅××

∫∫∫

rr r() (d )d

Vμ ωω ,

whence the remarkable relation

⋅=⋅KKdd

ωω .

(14.1.31)

Taking into account (11.2.29') and (14.1.31), we have

()

() ()

111

dd d d d d

222

OOO

TI I II

ΔΔΔΔ

ωω ωω⋅= ⋅= = = =KKωω .

==vers

ΔΔ





(14.1.32)

In this case

()

=−

OP K





so that, using the above results,

()

⋅

⎛⎞

⋅= ⋅ − =

⎜⎟

⎝⎠

dd0

OP K K I





ωω

Hence, the pseudomoment of momentum

is along the normal OQ at O to the plane

Π, tangent at P to the ellipsoid of inertia (see Fig. 3.9) too).

We define a vector

====

vers

ΔΔ

(14.1.33)

which is situated along the same normal and is associated to the moment of inertia

tensor

. Taking into account (3.1.100), we can write, in components,

In Chap. 3, Sect. 1.2.6 we have introduced the ellipsoid of inertia as locus of the points

P for which

213

14 Dynamics of the Rigid Solid

iijj

JIx

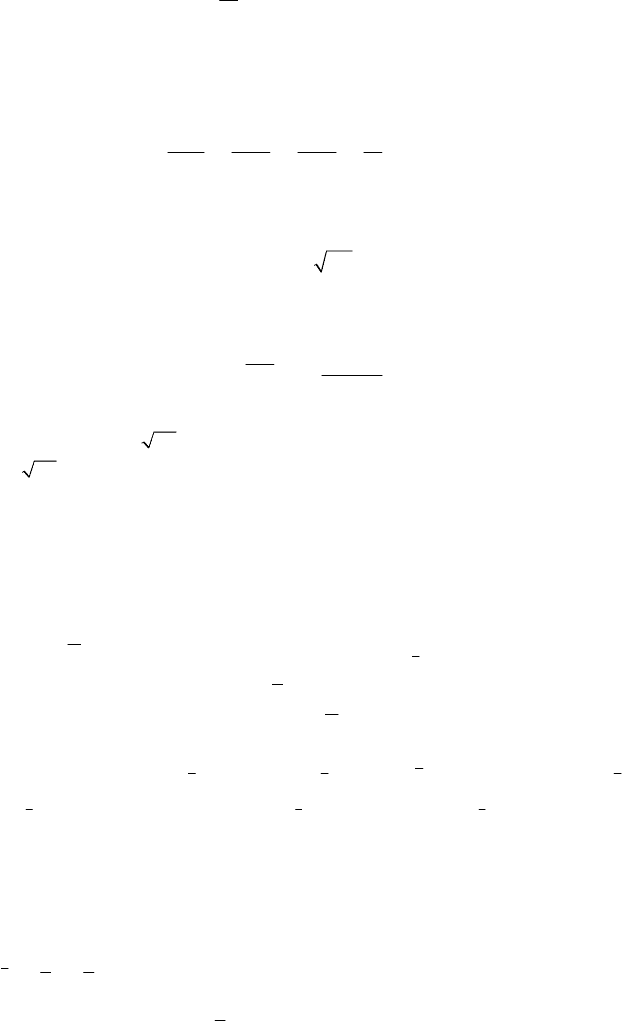
, = 1,2, 3i ,

(14.1.33')

where

x are the co-ordinates of the point P of the ellipsoid of inertia; we have, with

respect to the principal axes of inertia,

===

123

11 22 33

OOO

JJJ

Ix Ix Ix K

(14.1.33'')

Using the relation (3.1.82'), we get

⋅=J vers

ω .

(14.1.34)

We notice that (

∈Q Π

)

⋅

⋅= = =

OP J OQ K K





(14.1.34')

If we take

KRM

J /

applied at O is the point

′

(the inverse of the point Q with respect to a

sphere of centre O and radius R), the locus of which is the gyration ellipsoid; we obtain

this result also by comparing the relations (3.1.104') and (14.1.33''). It results thus a

graphic method to determine the pseudomoment of momentum

The relation (14.1.26') shows that the central moment of inertia tensor

plays an

important rôle. In this order of ideas, let be an axis which passes through the pole O

and let be

O another pole on , of position vector

αω

, α scalar, with respect to

the pole O. The relation

=+rrαω between the position vectors of a point P of the

rigid solid with respect to the poles O and

, respectively, allows to write

[]

()( ) ( )d ()d

O O

V V

VVμα α α μ=+××+=+××

⎡

⎤

⎣

⎦

∫∫∫ ∫∫∫

Krr rK rrωωω ωω

[]

()d ( ) ( )

OOO

VM KMαμ α α ω=+×× =+ ××=+ ⋅

⎡⎤

⎣⎦

∫∫∫

KrrK

ωω ωωρ ωρω−ρ.

If the axis is the principal axis of inertia with respect to the pole O, then

must be

collinear with , hence we must have

λω, λ scalar; if we wish that be a

principal axis of inertia with respect to the pole O too, analogously we must have

λω, λ scalar. In this case,

=+ ⋅ −

()MMλλα αωωω ωρω ρ

(see Chap. 3, Sect. 1.2.6), then the extremity of the vector

214

MECHANICAL SYSTEMS, CLASSICAL MODELS

ω ω

wherefrom it results

= βρω, β scalar. We can thus state that a principal axis of inertia

with respect to a given pole is a principal axis of inertia with respect to any point of it if

and only if it is a central axis of inertia. Analogously, let be a central principal plane of

inertia determined by the axes and

′

through O and a point O in this plane,

specified by the position vector

′′

+ααωω

, α,

′

α scalars; a point P of the rigid solid

will be specified by the position vectors

r and r with respect to the poles O and

respectively, so that

′′

=+ +

rrααωω . Putting the condition that the axes which pass

through

and are parallel to the axes and

′

be principal axes of inertia if the axes

and

′

have this property, then we find – as above – that

′′

ββρωω, β,

′

scalars; hence, a principal plane of inertia with respect to a given pole is a principal

plane of inertia with respect to any point of it if and only if it is a central principal

plane of inertia.

≡OC, then the relation (14.1.29') takes the form (11.2.37), where the

pseudokinetic energy is given by

()

′

=⋅ =⋅ =⋅

KK I

111

222

T ωωωω.

(14.1.35)

If we eliminate the pseudomoment of momentum

and the pseudokinetic energy

T between the relations (14.1.23'), (14.1.29') and (14.1.30') and take into account

(14.1.17'), then we find the remarkable relation

() ()

11 11

22 22

OCOOOCC

TM M

′ ′ ′′ ′ ′ ′′ ′

=⋅+ ⋅−×=⋅+ ⋅−×

KvvrKvvωωωωρ

(14.1.36)

analogous to the relation (14.1.17').

Introducing the transportation kinetic energy of the rigid solid

S, in the non-inertial

frame of reference

R, with respect to the inertial frame

′

, given by (11.2.41), we

notice that

′′

(tr )TTO,

(14.1.29'')

corresponding to the formula (14.1.29'). In the case of the rigid solid we have

= 0T ,

the comoment given by the kinematic torsor with the torsor of momenta vanishing too

(

=(,) 0τT ); in this case, the formula (11.2.43) leads to

()

′′

′

τT .

(14.1.29''')

In case of the free rigid solid

S, the elementary work of the given internal forces

vanishes. The elementary work of the given external forces is expressed in the form (we

assume that a system of n given forces is acting)

215

14 Dynamics of the Rigid Solid

()

11 1

dd d d

nn n

ii i ii

ii i

== =

⎛⎞

′′ ′

=⋅= ⋅+ ×⋅

⎜⎟

⎝⎠

∑∑∑

Fr F r rFω ,

where we have used the formula (11.2.10') and we have made

=r0d

and =v0

Introducing the torsor of the given external forces (

{

}

{

}

τ=FRM,

) and taking

into account the properties of the triple scalar product, we can write

dd d

′′

=⋅ + ⋅

Rr M ω ,

(14.1.37)

obtaining thus the expression of the elementary work of the given external forces in

case of a free rigid solid; we get the same result if we make

′

== =

int int

ddd0WWW and equate to zero the quantities connected to the

constraint forces in the relation (11.2.31). For the power of the given forces we have

(corresponding, analogously, to the formula (11.2.31'))

′′

=⋅ + ⋅

Rv M

P ω,

(14.1.37')

which allows to state

Theorem 14.1.8 The power of the given external forces which act upon a free rigid

solid, with respect to a given frame of reference, is equal to the power of the torsor of

these forces at an arbitrary pole, rigidly linked to the rigid solid, with respect to the

same frame.

Introducing the kinematic torsor (11.2.33), we can express the relation (14.1.37') also

in the form

{

}

()

′

=τ

′

P T .

(14.1.37'')

Starting from the theorem of momentum written in the form (12.1.33) for a

continuous mechanical system and using the expression (14.1.21'), (14.1.21'') for the

momentum of the rigid solid

S, we may write

()

′

′′

= = +×+××=

va R

MMM M



ωρ ω ωρ ;

(14.1.38)

this result can be expressed also in the form (

′

RR, the resultant being invariant to a

change of pole)

+=FR0

()c

(14.1.38')

where we have introduced the transportation complementary force

()

[]

′

=− +×+× ×

()c



ωρ ω ωρ,

(14.1.38'')

14.1.1.7 General Theorems

216

MECHANICAL SYSTEMS, CLASSICAL MODELS

corresponding to the mass centre. The above formulae can be obtained also from the

formulae (11.2.11'), (11.2.12), where we make

=H0, ∂∂=0/ tρ ,

()C

=F0,

=R0. Introducing the acceleration of the mass centre with respect to the inertial

frame of reference

′

R , it results

′

M .

(14.1.39)

We can thus state:

Theorem 14.1.9 (theorem of momentum) The derivative with respect to time of the

momentum of a free rigid solid, in an inertial frame of reference, is equal to the

resultant of the given external forces which act upon that solid.

Theorem 14.1.9' (theorem of motion of the mass centre) The centre of mass of a free

rigid solid moves, with respect to an inertial frame of reference, as a free particle at

which would be concentrated the whole mass of the solid and which would be acted

upon by the resultant of the given external forces.

Analogously, we use the theorem of moment of momentum written in the form

(12.1.33') for a continuous mechanical system, the moment of momentum of the rigid

solid

S being given by (14.1.23'); we obtain

()

[]

′

′′′′′ ′

=+ ×+×−×−××=

vvraa v M

OCOCO O

ρωρ

the moment of the given external forces being

′

=+×

MMrR

. Taking into

account (14.1.17') and (14.1.39), it results

()

′

×+=

ρ ,

(14.1.40)

a relation of the form (11.2.18), where we make

=M0

. We state

Theorem 14.1.10 (theorem of moment of momentum) The derivative with respect to

time of the pseudomoment of momentum of a free rigid solid with respect to an

arbitrary pole O, rigidly connected to the solid, in an inertial frame of reference, is

equal to the resultant moment of the given external forces which act upon this solid,

with respect to that pole, from which we subtract the dynamic moment, in the inertial

frame of the considered pole, translated at the centre of mass of the rigid solid, at

which is assumed to be concentrated the whole mass of this solid, taken with respect to

the pole O.

The relation (14.1.24') allows also to write

()

′

×+ =

aIM

()

OOO

ρω.

(14.1.40')

If the non-inertial frame of reference

R is of Koenig type ( = 0ω ), then the rigid solid

S has a motion of translation and we remain with the relation

217

14 Dynamics of the Rigid Solid

()

′

×=

Mρ .

(14.1.41)

If we have

≡OC (hence, = 0ρ ), then it results that the non-inertial frame of

reference is a Koenig frame; we can have a motion of translation of the free rigid solid

if and only if

=M0

. We notice that we can have =M0

even if the pole O does

not coincide with the centre of mass, if this pole has a uniform and rectilinear motion

with respect to an inertial frame or if the support of the acceleration

′

of the pole O

with respect to an inertial frame passes through the mass centre C. But if

≡OC with

≠ 0ω , then the theorem of moment of momentum becomes

()

[]

==IM

ωS ,

(14.1.41')

without any loss of generality. We obtain the same result starting from the relation

(11.2.24), where we make

=K0

and =M0

. Taking into account the relation

(14.1.26') too, we state, as well,

Theorem 14.1.10' The derivative with respect to time of the moment of momentum of a

free rigid solid, with respect to its mass centre, in an inertial frame of reference, with

respect to this frame, is equal to the resultant moment of the given external forces

which act upon this solid, with respect to the mass centre.

′

=⋅ + ⋅

Rv M

(14.1.42)

There results

Theorem 14.1.11 (theorem of kinetic energy). The derivative with respect to time of the

kinetic energy of a free rigid solid, in an inertial frame of reference, is equal to the

power of the given external forces considered to be applied at an arbitrary pole, rigidly

linked to the solid, with respect to the given frame.

Taking into account (14.1.29'), we are led to

()()( )

[]

′′ ′ ′ ′ ′

+⋅+ + + ×=⋅+⋅va a v v Rv M

,, ,, ,

OOOOO OO



ωρ ωρ ω,ω ρ ω

and the formula (14.1.38) allows to write the theorem of kinetic energy in the form

()

′

+=⋅aM

ωρ ω

(14.1.43)

corresponding to the relation (11.2.34); starting from the relation (14.1.30'), we are led

()

[]

() () ()

=+×⋅+ ⋅= ⋅+ ⋅II I I I

d1 1 1 1

d2 2 2 2

OO O O O



ωω ω ω ωω ωω ωω

Starting from the theorem of kinetic energy stated in, Sect. 11.2.2.2, we obtain

218

MECHANICAL SYSTEMS, CLASSICAL MODELS

wherefrom, taking into account (14.1.31), it results

() ()

=⋅=⋅II



ωω ωω

(14.1.43')

If we write the relation (14.1.43') in the form

=⋅Kdd

T ω , then we notice that

we have

=K grad

(14.1.44)

too, where

= ()

TTω . Analogously, starting from the relation (14.1.29'),

considering successively that

()

′′′

TT ,

′′

()TTω and taking into account

(14.1.21'), (14.1.26), we may write

′′′

=⋅

Hvdd

T and

′′

=⋅

Kdd

T ω ,

respectively, so that

′

′′

H grad

′′

K grad

(14.1.44')

Observing that the kinetic energy

′

T is a homogeneous function of second degree with

respect to the components of the vectors

′

and , Euler’s theorem allows to write

′

′′ ′ ′′′ ′

=⋅ +⋅ =⋅+⋅

vvHK2 grad grad

OOO

TTT

ωω

(14.1.44'')

finding thus again the relation (14.1.29''').

≡OC

, then the relation (14.1.43) becomes

()

[]

()

[]

=⋅=⋅=⋅IIM

CC C



ωω ωω ωSS ,

(14.1.43'')

without any loss of generality concerning the result.

A scalar product of the formula (14.1.41') by leads to the formula (14.1.43'');

obviously, by a scalar product of the formula (14.1.40) by , we get, analogously, the

relation (14.1.43). Because one can obtain the formula (14.1.43) taking into account the

theorems of momentum and of motion of the mass centre, respectively, we can state that

the theorem of kinetic energy is obtained as a linear combination of the theorems of

momentum and moment of momentum; consequently, it represents a supplementary

non-independent equation of motion. However, the theorem of kinetic energy is

important by itself; it can be used directly in various applications (e.g., in the study of

motion of the rigid solid with a fixed axis). One can also show that, starting from the

theorem of kinetic energy, we find again the theorems of momentum and moment of

momentum, because the relation (14.1.42) must hold for any rototranslation

()

′′

≡

vωT , according to the relation (14.1.29''').

219

14 Dynamics of the Rigid Solid

The theorems of momentum and moment of momentum constitute together the

theorem of torsor for a free rigid solid

S ; these theorems lead to two vector differential

equations or to six scalar differential equations and describe, entirely, the motion of the

rigid solid, which has six degrees of freedom. Indeed, taking into account the principle

of variation of the kinetic torsor for a continuous mechanical system, which can be

applied to an arbitrary subsystem

⊂S S , and observing that if we know the motion of

the subsystem S, then we know the motion of the whole rigid solid

S, we obtain the

same result. In vector form, these equations are

()

[]

′

+×+× × =



ωρ ω ωρ ,

(14.1.45)

()

′

×+ +× =

aI I M

OO O O



ρωωω,

(14.1.46)

while, in components, we obtain

()

′

+∈ +∈ ∈ =

Oi ijk k ijk klm l

Ma Rωρ ωωρ



, = 1,2, 3i ,

(14.1.45')

′

∈++∈=

jijj j

ijk Ok ijk kl l Oi

Ma I I Mρω ωω



, = 1,2, 3i ;

(14.1.46')

these equations can be written also in the form

[

]

()

′

+∈ + =2

jji i

Oi ijk k

Ma Rωρ ωω ρ



= 1,2, 3i

(14.1.45'')

()

′

∈++∈=

ijk Ok kl ik l ijk l Oi

Ma I Mρδωωω



, = 1,2, 3i .

(14.1.46'')

With respect to the principal axes of inertia, we get

()

′′

−++− =

23 113223

32 1

OO O

Ma a I I I Mρρ ω ωω



()

′′

−++− =

31 221331

13 2

OO O

Ma a I II Mρρ ω ωω



()

′′

−++− =

12 332112

21 3

OO O

Ma a I I I Mρρ ω ωω



(14.1.46''')

where

≥≥

123

III are the principal moments of inertia relative to the pole O.

Assuming that

≡OC, the equations of motion of the free rigid solid become

′

(14.1.47)

()

+× =IM

CCC



ωω ω ;

(14.1.48)

with respect to the central principal axes of inertia, we get

′

Ma R , = 1, 2, 3i ,

(14.1.47')

()

+− =

() () ()

123

132

CCC

III Mωωω



()

+− =

() () ()

231

213

CCC

III Mωωω



()

+− =

() () ()

312

321

CCC

III Mωωω



(14.1.48')

14.1.1.8 General Equations of Motion

220

MECHANICAL SYSTEMS, CLASSICAL MODELS

where

≥≥

() () ()

123

CCC

III are the central principal moments of inertia. The equations

(14.1.46''') take the form (14.1.48') with respect to an arbitrary point O of the rigid solid

too, if this point has a uniform and rectilinear motion (

′

=a0

) with respect to an

inertial frame of reference or if the support of the acceleration of this point passes at

any time through the mass centre C; this form of the equations of the motion of rotation

of the rigid solid

S about a point of it is due to L. Euler.

We have seen that the theorem of kinetic energy is a linear consequence of the

theorem of torsor; this theorem can be used to obtain a first integral of the system of

equations of motion. In the non-inertial frame of reference

R, the relation (14.1.43)

takes the form

()

111 222 333 1 2 3

123

ijk Oi k O O O

II I Ma MMMωω ωω ωω ωρ ω ω ω

′

++ +∈ =++



(14.1.49)

with respect to the principal axes of inertia; if

≡OC, then the relation (14.1.49)

becomes (corresponding to the relation (14.1.43'''))

()

++ =++

() () ()

11 22 33 1 2 3

123

CC C

CCC

III MMMωω ωω ωω ω ω ω



(14.1.49')

Because all the above equations are written with respect to the non-inertial frame of

reference

R, rigidly linked to the solid, the acceleration of the pole of this frame must

be expressed analogously. Hence,

′

′′

==+×

avv

OOO

 ω

′

′′

==+×

avv

CCC

 ω

(14.1.50)

where we have put into evidence the derivatives

′′

=vv/

t∂∂



and

′′

=vv/

t∂∂



of the velocities

′

and

′

with respect to time, respectively. The equations

(14.1.45), (14.1.46) take the form

()

[]

′′

+× +× +× =vv R



ωωρωρ,

(14.1.51)

()()

′′

×+×++× =vvI IM

OOO OO



ρω ωωω,

(14.1.51')

while the equation (14.1.47) becomes

()

′′

+× =vvR



ω .

(14.1.52)

From the above considerations, we notice that the motion of the free rigid solid does

not depend on the action of each external force, taken separately, but only on the torsor

of all the forces with respect to an arbitrary point of it (the pole of the non-inertial frame

of reference

R ); hence, two equivalent systems of forces (modelled as sliding vectors)

applied upon a free rigid solid lead to the same motion of it. In the modelling as a

221

14 Dynamics of the Rigid Solid

particle of the rigid solid, its motion is reduced to the motion of translation of its mass

centre C acted upon by the resultant

R, the number of degrees of freedom being

reduced from six to three. If one cannot neglect the rotation of the solid about the centre

C, then we introduce also the action of the resultant moment

, which specifies the

motion. Obviously, to can obtain such a decomposition, we must assume that

()

′′

=RR v,;

tρ , non-depending on and on Euler’s angles ψ, θ, ϕ; we can use thus

the equation (14.1.47) as a Newton equation of motion for a particle.

In general, we have

()

′′′′′′

123

123123

,,,,,,,,,,,;

OOOOOO

RRxxxvvv tψθϕω ω ω ,

()

′′′′′′

123

123123

,,,,,,,,,,,;

Oi Oi O O O O O O

MMxxxvvv tψθϕω ω ω , = 1, 2, 3i ,

the rigid solid being non-autonomous; if the time does not intervene explicitly, then the

solid is autonomous (or dynamic). The 12 unknown scalar functions (the co-ordinates

′′

= ()

Oi Oi

xxt of the pole O, the components

′′

= ()

Oi Oi

vvt of the velocity of the pole

O with respect to the inertial frame of reference

′

R , Euler’s angles = ()tψψ ,

= ()tθθ , = ()tϕϕ and the components = ()

tωω, = 1, 2, 3i , of the instantaneous

angular velocity vector of the rigid solid with respect to the non-inertial frame of

reference

R ) are determined by the system of first order differential equations

(14.1.45''), (14.1.46'') and (14.1.15), written in the normal form (the coefficients of the

equations (14.1.53), (14.1.53') are constant and we can solve this linear system with

respect to the derivatives of first order)



[

]

′

+∈ = = −

iji

ijk k

MM RRM

ρωωρ

, = 1,2, 3i ,

(14.1.53)



′

∈+==−∈

jij j

ijk Oi ijk kl l

MIMMI

ρωω

, = 1,2, 3i ,

(14.1.53')

()( )

==+

1121 2

, , , sin cos cosec

θϕω ω ω ϕ ω ϕ θ

()

==−

212 1 2

,, cos sin

ϕω ω ω ϕ ω ϕ

()( )

312331 2

,, , , sin cos cot

θϕω ω ω ω ω ϕ ω ϕ θ==−+

(14.1.53'')

to which we associate the equations

()

′

′′′′′

123

,,;

Oi Oi O O O

vvxxxt

, = 1,2, 3i ,

(14.1.53''')

the derivatives being taken in the inertial frame of reference

′

R , as well as the initial

conditions (at the moment

tt) of Cauchy type

()

′′

Oi Oi

xt x,

()

′′

Oi Oi

vt v,

()

tψψ,

()

tθθ,

()

tϕϕ,

()

tωω, = 1, 2, 3i .

(14.1.54)

222

MECHANICAL SYSTEMS, CLASSICAL MODELS