Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems
Подождите немного. Документ загружается.

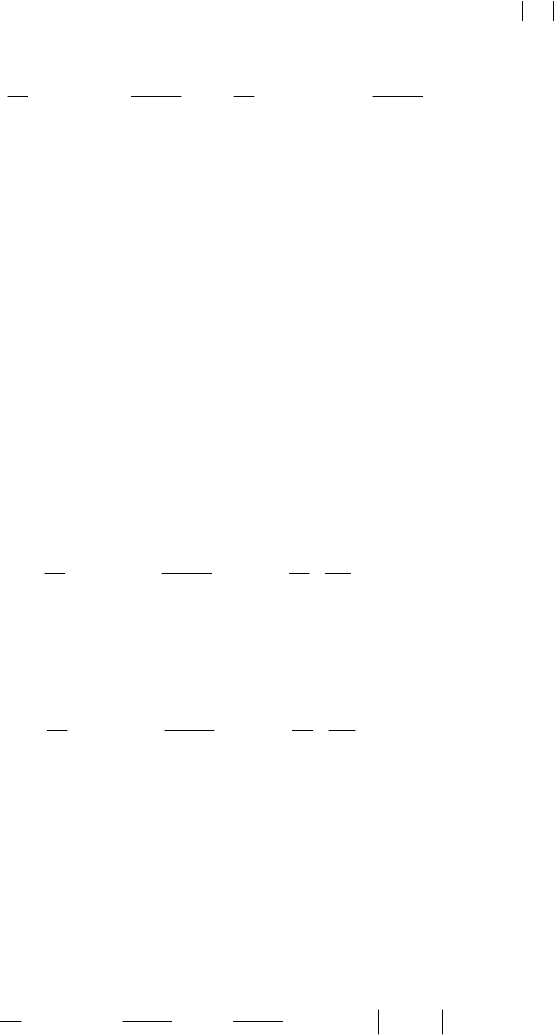
12
/Ufmmr=− ) being, in this case, given by
3
1212
/
f
mm r=Fr,
12
r = r , where f
is the constant of universal attraction. The equations of motion are
12
11 12
3
d
()
d
mm
mf
t
r
=vr
,
12
22 12
3
d
()
d
mm
mf
t
r
=−vr
.
(13.2.25)
Using the theorems of momentum and moment of momentum in the form (13.2.8''') and
in the form (13.2.15''), respectively, and observing that the external forces vanish
(
=R0,
O
′
=M0), we can state conservation theorems of momentum and of moment
of momentum, respectively; there result the first integrals
11 22 1
mm+=vvC, (13.2.26)
111222 2
() ()mm×+× =rvr vC,
(13.2.26')
where
12
,const=
CC . We can write the identity
1221 122221122
()( ) ( )mm m m m m m m−= + − +vv v v v.
Observing that
2112
−=
vvr, taking into account (13.2.26) and eliminating the
momentum
22
m v between this relation and the second equation (13.2.25), we obtain
the vector equation
12
12 12 1
3
1
dd
()
dd
mm
m
mf
ttm
r
⎛⎞
++ =
⎜⎟
⎝⎠
rrC0,
(13.2.27)
where
12 1 2
/( )mmm m m=+ is the reduced mass; this equation characterizes the
motion of the particle
2
P
with respect to the particle
1
P
. Analogously, we can write
12
21 21 1
3
2
dd
()
dd
mm
m
mf
ttm
r
⎛⎞
++ =
⎜⎟
⎝⎠
rrC0
(13.2.27')
too, this last equation characterizing the motion of the particle
1
P with respect to the
particle
2
P . In particular, if the masses
1
m and
2
m are constant in time, we find again
the classical equations (8.1.14).
The case
n = 3 (the problem of three particles) has been considered in 1932 in the
same conditions, using the above ideas, due to I.I. Plăcinţeanu. Let thus be the particles
i
P
of position vectors
i
r , with respect to an inertial frame of reference, and variable
masses
i
m , 1, 2, 3i = ; the equations of motion are
33
d
()
d
ij
i
k
ii ij
ik
ij
ik
mm
mm
mf f
t
rr
=+vrr
,
ij j i
r =−rr
,
ijki≠≠≠
,
,, 1,2,3ijk=
.
(13.2.28)
13 Other Considerations on Dynamics of Mechanical Systems
183

MECHANICAL SYSTEMS, CLASSICAL MODELS
As in the preceding case, we obtain the first integrals
11 22 33 1
mmm++ =vvvC, (13.2.29)
111222333 2
() () ( )mm m×+× +× =rvrvr vC,
(13.2.29')
where
12
,const=
CC . We can write the identities
1221 122221122
()( ) ( )mm m m m m m m−= + − +vv v v v,
1331 133331133
()( ) ( )mm m m m m m m−= + − +vv v v v;
taking into account (13.2.28), (13.2.29), introducing the mass
123
Mm m m=++ of
the discrete mechanical system and eliminating the momenta
22
m v and
33
m v , we
find, as in the case
2n = , the equations of motion of the particles
2
P and
3
P with
respect to the particle
1
P in the form
(
)
(
)
22312
212 13 12
3
12
dd
1
dd
mmmmm
mf
tMtM
r
⎡⎤
−− +
⎣⎦
rrr
(
)
23 2
32 1
3
23
d
d
mm m
f
tM
r
++ =rC 0
,
(
)
(
)
32313
313 12 13
3
13
dd
1
dd
mmmmm
mf
tMtM
r
⎡⎤
−− +
⎣⎦
rrr
(
)
23 3
23 1
3
23
d
d
mm m
f
tM
r
++ =rC 0
.
(13.2.30)
Summing these two equations, we find (we have
23 32
+=rr 0)
()
(
)
112131
2 12 3 13 12 13 1
33
12 13
dd
dd
mmmmmm
mm f f
tM tM
rr
⎡⎤
++ + − =
⎣⎦
rr r rC 0
;
(13.2.30')
this equation, together with one of the equations (13.2.30), constitute a system of two
differential equations for the problem of three particles of variable mass. Unlike the
equations (13.2.30), the equation (13.2.30') contains only two unknown vector
functions (
12 12
()t=rr and
13 13
()t=rr); we notice that we can write the latter
equation in the form of two equations
(
)
(
)
12 12 2
12 12 1
3
12
dd
()
dd
mm mm m
f
t
tM tM
r
++ =
rrCC
,
(
)
(
)
13 13 3
13 13 1
3
13
dd
()
dd
mm mm m
f
t
tM tM
r
++ =−
rrC C
,
(13.2.31)
of the form (13.2.27), where the function
()tC remains to be determined. Subtracting
one equation (13.2.30) from the other and taking into account (13.2.31), we get (we
notice that
13 12 23
−=rr r)
184

(
)
23 23
23 23
3
23
d
()
d
mm mm
f
t
tM
r
+=
rrC
.
(13.2.31')
Thus, the differential equations of the problem will be (13.2.31), (13.2.31'), having a
more symmetrical form, by separation of variables.
In the case of an arbitrary number
n of particles, we use the equations of motion
(
ij ij j j
r ==−rrr)
3
1
d
()
d
n
j
ii i ij
j
ij
m
mfm
t
r
=
=
∑
vr
, ji≠ , 1,2,...,in= ;
(13.2.32)
we obtain the first integrals
1
1
n
ii
i
m
=
=
∑
vC
,
(13.2.33)
2
1
()
n
iii
i
m
=
×=
∑
rvC.
(13.2.33')
Let us make a change of function and of variable
() () ()
ii
t ϕτ τ=r
ρ
, d()dttτψ=
and introduce the notations
d/dϕϕτ
′
=
, d/d
ii
τ
′
=
ρρ
,
1,2,...,in=
; we can
calculate
()
iii
ψϕ ϕ
′′
=+v
ρρ
,
()()
22 2
2
ii i i
ψϕ ψϕ ψϕ ψϕ ψϕ
′′ ′ ′ ′ ′′
=++ ++
v
ρρρ
.
The equations of motion (13.2.32) become (
ij j i
=−
ρρρ
)
()
[
]
()
[
]
22 2
2
ii i i i i i i
mm m m mψ ϕ ψϕ ψ ϕ ψϕ ψ ϕ ψϕ ψϕ
′′ ′ ′ ′′ ′ ′
+++ + ++
ρρ ρ
,
23
1
1
n
ij
ij
j
ij
mm
ρρ
=
=
∑
ρ
,
ij≠
,
1,2,...,in=
;
we impose the conditions
2
d
()2 0
d
ii
mm
t
ψϕϕϕ
′
+=
,
2
d
() 0
d
ii
mm
t
ψϕϕϕ
′′′
+=
,
which can be written also in the form
1d
ln( ) 2 0
d
i
m
t
ϕ
ψ
ϕϕ
′
+=
,
1d
ln( ) 0
d
i
m
t
ϕ
ψ
ψϕ
′′
+=
′
.
We notice that we must have
2/ / constϕϕ ϕ ϕ
′′′′
==
, which can take place only if
kϕ = , constk = , 0ϕϕ
′′′
==
; in this case, it results
ii
mψμ= , const
i
μ = , and
we assume that
13 Other Considerations on Dynamics of Mechanical Systems
185

MECHANICAL SYSTEMS, CLASSICAL MODELS
0
() ()
ii
mt mft=
,
1
()
()
ft
t
ψ
= ,
0
const
i
m =
,
1,2,...,in=
.
(13.2.34)
The equations of motion (13.2.32) become (
()
ii
τ=
ρρ
, ()
ij ij
τ=
ρρ
)
00
3
0
33
1
()
n
ij
ii ij
j
ij
mm
ft
m
k ρ
=
′′
=
∑
ρρ
, ji≠ , 1,2,...,in= ,
(13.2.32')
obtaining the form of classical equations, corresponding to constant masses. It results
0
1
n
ii
i
m
=
′′
=
∑
0ρ
,
wherefrom
1
0
11
11
()
() ()
nn
ii ii
ii
mmMt
kf t kf t k
τ
==
===+
∑∑
C
r Cρρ
,
so that (
ρ is the position vector of the centre C)
1
0
k
M
τ +
=
CC
ρ
,
0
0
1
1
()
n
i
i
MM m
ft
=
==
∑
,
(13.2.35)
the centre of mass having a rectilinear trajectory; we have
1
11
00
11d1
() d () ()
C
f
tMtMft Mt
τ
′
== = =
C
vCCρ
,
(13.2.35')
the velocity
()
CC
t=vv being constant only if () const
f
t = , and
1
C being the
constant of the first integral of the momentum (13.2.33). Hence, we can state that, in
case of a discrete mechanical system
S of masses having the same variation in time
(
0
() ()
ii
mt mft= ,
0
const
i
m = , 1,2,...,in= ), the centre of mass C has a rectilinear
and non-uniform motion; the motion of the centre
C is uniform only in case of constant
masses.
13.3.2.3 Motion of an Artificial Celestial Body
Let be, for instance, an artificial celestial body
B, which is launched from the Earth E
and which moves away from our planet; this body can enter in the zone of attraction of
another body of the solar system, e.g., in the attraction zone of the Sun
S. We have thus
a problem of three particles (Earth
E, Sun S and artificial celestial body B); if the mass
m of the body B can be neglected with respect to the mass
E
m of the Earth
186
(
E
mm
) and to the mass
S
m of the Sun (
S
mm
), then we can assume some
approximations of computation.
To fix the ideas, we will consider the motion of the body
B on the straight line which
joins the centre of mass
E of the Earth to the centre of mass S of the Sun, assuming that
the two celestial bodies are fixed (Fig. 13.11); the equation of motion is of the form
22
d
d
()
ES
BE BS
mm mm
v
mFF f f
t
xsx
=+=− +
−
,
(13.2.36)
where
s is the distance from the Earth to the Sun, while x is the abscissa of the centre of
mass of the body
B with respect to the Earth E, chosen as origin. Observing that
d/d d/dvtvvx= and integrating, we obtain the first integral of the mechanical
energy
Fig. 13.11 Motion of an artificial celestial body
(
)
2
2
ES
mm
vf h
xsx
=++
−
,
2
00
2
ES
mm
hv f
xsx
⎛⎞
=− +
⎜⎟
−
⎝⎠
,
(13.2.36')
where
0
(0)xx= ,
0
(0)vv= , corresponding to the initial moment
0t =
. From
(13.2.36) one observes that for
x sufficiently small we have 0v <
, hence the velocity
decreases till the body
B reaches a point Q, the abscissa of which is given by
2
/( ) /
QQ ES
xsx mm− =
⎡⎤
⎣⎦
, hence by
1
1
Q
S
E
ss
xs
m
m
==≅
+
+
,
2
E
S
m
m
=
,
(13.2.37)
taking into account that
26
310
−
≅⋅ , hence
3
1.732 10
−
≅⋅ ; because
4
2.348 10sR=⋅, where
8
6.38 10 cmR =⋅ is the radius of the Earth, we obtain
3105
1.729 10 s 40.579 2.590 10 cm 2.59 10 km
Q
xR
−
≅⋅≅ ≅⋅ =⋅
.
13 Other Considerations on Dynamics of Mechanical Systems
187

MECHANICAL SYSTEMS, CLASSICAL MODELS
If the initial velocity
0
v is too small, the velocity of the body B can vanish before
reaching the point
Q; in this case, the velocity changes of sign, so that the body returns
on the Earth. Observing that the second cosmic velocity is given by
2822
0
2 / 1.249700 10 m / s
II E
vfmx=≅⋅, we can write the relation (13.2.36') also in
the form
22 2
00
2
00
11 1 1 1
II
vvxv
x x sxsx
⎡
⎛⎞⎤
=+ −+ −
⎜⎟
⎢
⎥
−−
⎣
⎝⎠⎦
;
(13.2.36'')
for numerical data, it results the approximate formula
22 2 22
00
0.951
QII
vv v vV=− =−
,
(13.2.38)
where
22
0.951
II
Vv= , hence 0.975 10.902km/s
II
Vv≅≅ . If
0
vV< , then the body
B does not reach Q, returning on the Earth, while if
0
vV>
, then the body B reaches
Q with a non-zero velocity 0
Q
v > and passes through this position, continuing its way
towards the Sun with a monotone increasing velocity.
If, in particular,
0
vV= , then the body B reaches Q with a null velocity ( 0
Q
v = );
the point
Q represents thus a position of equilibrium, namely a labile position of
equilibrium, because an arbitrary perturbation of the position of equilibrium (towards
E
or towards
S), moves away the body B from this position. The moment at which the
body
B reaches Q is given by
0
d
()
Q
x
Q
x
x
t
vx
=
∫
;
(13.2.39)
observing that
0
xx= is a double root of () 0vx = , we can write
0
2
()
d
()
Q
x
Q
x
Q
f
x
tx
xx
=
−
∫
(13.2.39')
too, where
f (x ) is a regular function in the neighbourhood of the point
0
xx= . The
integral (13.2.39') is improper, so that the time
Q
t is infinite; the body B comes near to
the position
Q, but never reaches it.
Obviously, in the above modelling, the hypothesis of rectilinearity represents an
approximation; as well, we have assumed that the masses are constant. However, the
results thus obtained are useful from a qualitative point of view.
188
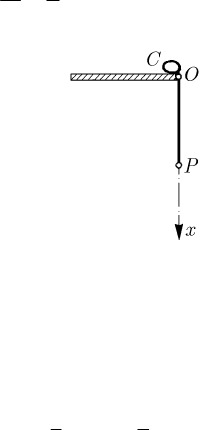
13.2.3 Continuous Mechanical Systems
One meets, frequently, interesting problems where one deals with continuous
mechanical systems of variable mass, e.g.: the problem of a captive balloon, the
problem of a glacier or of an iceberg the mass of which diminishes by melting, the
problem of an airplane which flies during snowfall (the mass of the snow-flakes is
added to the mass of the airplane) etc.; more difficult are the problems in which one
must take into account the deformability of the mechanical system. In what follows, we
consider two such problems: Cayley’s problem, which has merely a historical interest,
and the problem of the winch, which has a particular practical interest, using various
approximations of calculation.
13.2.3.1 Cayley’s Problem
In 1857, Cayley considered the problem of a heavy homogeneous chain, wrapped up on
the cylinder
C, at rest on a horizontal table; we assume that the chain falls along the
vertical, due to its own weight. Let be
x the abscissa of the movable end P of the chain,
the origin being taken at the level of the table, while the
Ox-axis is directed towards the
descendent vertical (Fig. 13.12); the equation of motion of this point is
()xxt= and,
approximating the whole chain by a particle of variable mass, we can use the theorem
of momentum in the form (13.2.8''') (the Levi-Civita case). We write thus
d
d
xx x
tg
γ
γ
⎡⎛ ⎞ ⎤
=
⎜⎟
⎢⎥
⎣⎝ ⎠ ⎦
,
(13.2.40)
Fig. 13.12 Cayley’s problem
where
γ is the unit weight, while ()xxt=
is the velocity of the chain (the same for all
its elements). Observing that
d/d d/dtx x=
, we can write
2
d( )/dxx xx x gx=
,
wherefrom, by integration,
23
1
()
23
g
xx x=
,
the integration constant vanishing (we assume that the chain begins to wrap up from the
state of rest, so that
(0) 0x = , (0) 0x = ).
We deduce (
0x ≠ )
13 Other Considerations on Dynamics of Mechanical Systems
189
MECHANICAL SYSTEMS, CLASSICAL MODELS
d2
d
3
xg
t
x
=
,
so that
2/3/2xgt= ; hence,
2
()
6
g
xt t=
,
()
3
g
vt t=
,
()
3
g
at =
,
(13.2.40')
the motion of the elements of the chain being uniformly accelerated.
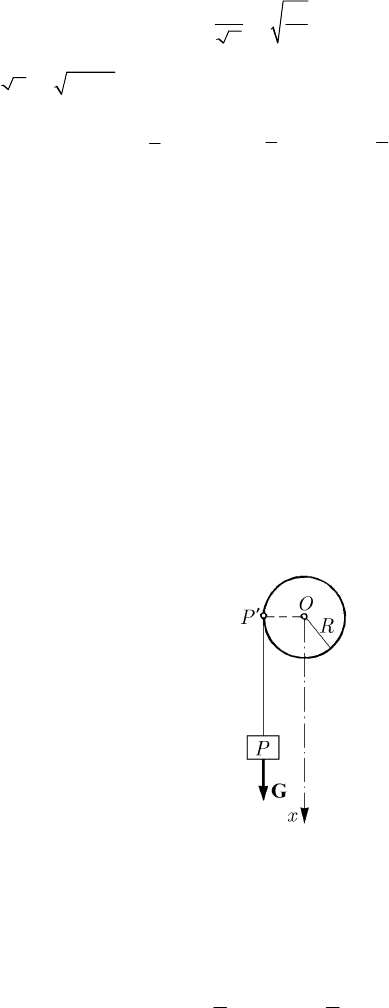
13.2.3.2 The Winch
The winch is a simple machine formed by a homogeneous cylinder of radius R, on
which is wrapped up an inextensible and non-torsionable homogeneous cable, of own
weight
γ; we assume that the winch rotates with an angular velocity ω around a
horizontal axle passing through
O, at the end of the cable being tied a weight m=Gg,
modelled as a particle, the equation of motion of which is
()xxt= (the Ox-axis is
along the descendent vertical; Fig. 13.13). The moment of momentum with respect to
the fixed pole
O is given at the moment t by (the phenomenon being unidimensional,
we consider only the non-zero component of the moment of momentum)
OO
KI mRvKω
′
=+ +
,
Fig. 13.13 Winch
where
()
OO
IIt= is the moment of inertia of the cylinder with respect to its axis at the
moment
t, ()Rmv is the moment of momentum of the weight G, while K
′
is the
moment of momentum of the unwrapped cable (the cable
PP
′
), given by
0
d
x
KRv Rvx
gg
γγ
ξ
′
==
∫
.
We notice that
190
02
() ()
OO
It It xR
g
γ
⎛⎞
=−
⎜⎟
⎝⎠
,
where
0
O
I is the moment of inertia of the cylinder on which is wrapped the cable (at the
initial moment
0t = ), while
2
(/)xgRγ is the moment of inertia of the cable which
was unwrapped; assuming that the unwrapping of the cable is without sliding friction,
we have
vRω= , so that it results
()
02
OO
KImRω=+
,
(13.2.41)
as the whole cable would be wrapped on the cylinder.
Applying the theorem of moment of momentum in the form (13.2.15'') (case
considered by Levi-Civita), we can write
()
02
() ( )
O
ImR xRmgRMMωγ+=+++
,
(13.2.42)
where
M is the moment of the driving couple, while M is the moment of the friction
couple of the winch with the axle about which it rotates. Supposing that
sign 2M αωβω=− −
, ,0αβ> ,
(13.2.43)
we put into evidence the Coulombian friction (case
0β = ), as well as the
hydrodynamic friction (case
0α = , where a lubricant is used). The differential
equation of the motion (13.2.42) takes the form (
//vR xRω == ,
//vR xRω ==
)
2xaxbxc+−= , ,, constabc= , ,0ab> , (13.2.44)
with the notations
02
O
a
ImR
β
=
+
,
2
02
O
R
b
ImR
γ
=
+
,
02
(sign)
O
RmgR M
c
ImR
αω+−
=
+
.
(13.2.44')
We obtain thus (the winch begins to move at the initial moment with the weight
G in
the upper position, hence with
(0) 0x = , (0) 0x = )
1
() e ( cosh sinh ) 1
at
c
xt a at a at
ba
−
⎡⎤
′′ ′
=+−
⎢⎥
′
⎣⎦
,
2
aab
′
=+,
(13.2.45)
as well as
() e sinh
at
c
xt at
a
−
′
=
′
,
(13.2.45')
13 Other Considerations on Dynamics of Mechanical Systems
191

MECHANICAL SYSTEMS, CLASSICAL MODELS
() e ( cosh sinh )
at
c
xt a at a at
a
−
′′ ′
=−
′
,
(13.2.45'')
all these quantities being positive for
t > 0. The motion of the winch is thus completely
determined.
192
