Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

then we find again Carnot’s generalized theorem, written in the form (10.1.47),

analogue to that in case of plastic collisions; as well, if

()

⎡⎤

′

⋅++ + =

⎢⎥

⎣⎦

∑∑

vPP PP 0

Ri ik Rik

(13.1.54')

then we can write an analogue of the generalized theorem of Carnot, in the form

(10.1.47').

Summing the relations (13.1.53) and (13.1.53'), it results

()

⎡

⎤

′′′

Δ= +⋅++ +

⎢

⎥

⎣

⎦

∑∑

vv PP P P

() '

ii i

Ri ik Rik

(13.1.55)

so that we can state

Theorem 13.1.9 (Kelvin). The variation of the kinetic energy of a discrete mechanical

system subjected to constraints, at a moment of discontinuity, is equal to the sum of the

scalar products of the percussions which act upon the particles by the semisum of their

velocities before and after the phenomenon of discontinuity.

If we subtract the relation (13.1.53') from the relation (13.1.53), then we obtain

()

⎡

⎤

=⋅+++

⎢

⎥

⎣

⎦

∑∑

vPP PP

()

Ri ik Rik

(13.1.55')

and we are led to

Theorem 13.1.9' (analogue of Kelvin’s theorem). The kinetic energy of the lost

velocities of a discrete mechanical system subjected to constraints, at a moment of

discontinuity, is equal to the semisum of the scalar products of the percussions which

act upon the particles by the jumps of their velocities at that moment of discontinuity.

Starting from the formula (13.1.8), we can write the relation

+−Δ=PP v 0

iii

, = 1,2,...,in, (13.1.56)

for a particle

P ; effecting a scalar product by the virtual displacements δr

at the

beginning of the interval of percussion and summing for all the particles of the

mechanical system

S, one obtains a necessary condition to describe the phenomenon of

collision

()

−Δ ⋅δ=

∑

Pvr

iii i

(13.1.57)

where we have considered that for the ideal constraints we have

⋅δ =

∑

(13.1.58)

corresponding to their relation of definition (3.2.36). Assuming that the condition

(13.1.57) is fulfilled and that

p holonomic constraints of the form (3.2.21'') and

13 Other Considerations on Dynamics of Mechanical Systems

153

MECHANICAL SYSTEMS, CLASSICAL MODELS

m non-holonomic constraints of the form (3.2.15) take place, we use the method of

Lagrange’s multipliers; we can thus write

===

′′

⎛⎞

−Δ+ ∇ + ⋅δ=

⎜⎟

⎝⎠

∑∑∑

Pv r

111

iii i i

ll kki

ilk

tt tt

mfλμα

where the Lagrange’s multipliers

λ , l = 1,2,…,p, and

′′′

kkk

μμμ

′

∫

()d

ttμμ,

′′

∫

()d

ttμμ

, = 1,2,...,km,

are non-determinate scalars and where we took into account that in a finite double sum

one can invert the order of summation. As in Sect. 11.1.2.10, we find again the relations

(13.1.56), the constraint percussions being given by

′′

=∇ +

∑∑

Ri l l k ki

tt tt

fλμα

, = 1,2,...,in.

(13.1.59)

The relation (13.1.57) becomes a sufficient condition too, and we can state

Theorem 13.1.10 (theorem of virtual work). The motion of a discrete mechanical

system subjected to ideal constraints, in the collision interval, takes place so that the

virtual work of the lost percussions which act upon that system vanishes for any system

of virtual displacements of the respective system.

We have used, in this theorem, the denomination of lost percussion for the difference

−ΔPv

iii

m which equilibrates the constraint percussion P

(by analogy to the

denomination of lost force of d’Alembert). As in the case of continuous mechanical

phenomena, this theorem can be considered as a principle (the principle of virtual work

or the principle of virtual displacements), because, starting from it, one can solve the

basic problems of the phenomenon of collision.

The equation (13.1.56) with (13.1.59) are Lagrange’s equations of the first kind for

the collision phenomenon.

Introducing the virtual velocities (3.2.1'), we can write the condition (13.1.57) in the

form

()

∗

−Δ ⋅ =

∑

Pvv

iiii

(13.1.57')

the considered principle being thus called the principle of virtual velocities too.

In case of a discrete mechanical system subjected to unilateral constraints, we can

express the principle of virtual work in the form

()

−Δ ⋅δ≤

∑

Pvr

iii i

(13.1.57'')

It is interesting to notice that the relation (13.1.57) allows to find again the theorems

of Carnot and Kelvin.

154

Starting from the form taken by the general theorems of mechanics in case of the

collision phenomenon, we can state some conservation theorems, particularly useful.

Thus, if

+=0RR

, then it results Δ=H0

() , obtaining

Theorem 13.1.11 (conservation theorem of momentum). The momentum of a discrete

mechanical system subjected to constraints is conserved in a collision interval if and

only if the resultant of the given and constraint external percussions which act upon the

system vanishes in that interval.

Analogously, if

+=0

MM , then it results Δ=K0

()

, and we can state

Theorem 13.1.12 (conservation theorem of moment of momentum). The moment of

momentum of a discrete mechanical system subjected to constraints, with respect to a

given pole, is conserved in a collision interval if and only if the resultant moment of the

given and constraint external percussions which act upon the system, with respect to

the same pole, vanishes in that interval.

Hence, if the given and constraint percussions which act upon a discrete mechanical

system subjected to constraints are equilibrated in their totality in the collision interval

(the mechanical system is considered as non-deformable), then the kinetic torsor of the

system is conserved in that interval.

Assuming that the relation

()

⎡⎤

′′′

+⋅++ + =

⎢⎥

⎣⎦

∑∑

vv PP P P

ii i

Ri ik Rik

(13.1.60)

takes place, the theorem of Kelvin allows to state

Theorem 13.1.13 (conservation theorem of kinetic energy). The kinetic energy of a

discrete mechanical system subjected to constraints is conserved in a collision interval

if and only if the sum of the scalar products of the given and constraint, external and

internal percussions which act upon the particles by the sum of their velocities before

and after a moment of discontinuity vanishes.

From (13.1.23), it results that the relation

Δ=

() 0T takes place in case of an

elastic collision (

k = 1). As well, from (13.1.60) we can state that the conservation

Theorem 13.1.13 can be obtained if

′′ ′

=−

, i = 1,2,…,n, or if the given and

constraint, external and internal percussions are equilibrated for each particle of the

mechanical system (considered as non-deformable).

13.1.2 Elastic and Plastic Collisions of Discrete Mechanical Systems

In the following, we consider the general case of elastic and plastic collisions of the

particles, including the problems at the atomic level. The case of plastic collisions is

studied by introducing the space of plastic collisions.

13.1.2.1 Elastic Collisions of Particles. Disintegration and Diffusion of Particles.

Rutherford’s Formula

Let be two particles

P and

P of masses

m and

m , respectively, having the

velocities

′

and

′′

before and after the interaction, respectively (it is

assumed that the particles come from infinite and tend to infinite). In the absence of

13 Other Considerations on Dynamics of Mechanical Systems

155

MECHANICAL SYSTEMS, CLASSICAL MODELS

percussions, we can write a conservation theorem of momentum (corresponding to the

formulae (1.1.26)) and a conservation theorem of kinetic energy in the form

′ ′ ′′ ′′

+=+vvvv

11 22 11 22

mm mm

′ ′ ′′ ′′

+=+

22 2 2

11 22 11 22

mv mv mv mv

(13.1.61)

We notice that these relations can be written also in the form

()( )

′′ ′ ′′ ′

−+ − =

vv vv 0

11 1 22 2

()()()()

′′ ′ ′′ ′ ′′ ′ ′′ ′

−⋅++ −⋅+ =

vv vv vv vv

11 1 1 1 22 2 2 2

0mm

Denoting

()()

′′ ′ ′′ ′

=−=−−

uvv vv

11 1 22 2

mmλ

, =u 1 , λ scalar, and introducing the

relative velocities

′′′

=−

vv v

′′ ′′ ′′

=−

vvv

, (13.1.62)

we find

′′′

⋅⋅=uv+uv 0

and

′′ ′

=−

vv u(/ )mλ , where we introduce the reduced

mass

m given by (8.1.14); a scalar product of the latter relation by u leads to

2mλ

′

=⋅uv and

′′ ′ ′

=−

⋅

vv uvu2( ) . The velocities after interaction can be thus

expressed as functions of the velocities before interaction in the form

′′ ′ ′

=+ ⋅vv uvu

2( )

′′ ′ ′

=− ⋅vv uvu

2( )

;

(13.1.63)

as well, we can write

′′′ ′′

=+ ⋅vv uvu

2( )

′′′ ′′

=− ⋅vv uvu

2( )

(13.1.63')

In case of the phenomenon of diffraction considered in Chap. 8, Sect. 1.2.1,

=±u versOQ





; assuming that

′

⋅>

uv 0 , we have

′′

⋅=

uv sin( /2)v  , where  is

the diffraction angle.

The problem considered above is also called the problem of biparticle collision. One

assumes that the two particles are, at the initial moment, at a great distance one of the

other, so that each one of these particles can be considered as being free; if during the

motion the particles become nearer, then interaction forces arise, becoming in real

(collision or capture) or fictitious (diffusion or diffraction) contact. Using the velocity

of the mass centre (invariant in the collision interval, in conformity to the

conservation theorem of momentum – first relation (13.1.61))

′′ ′′

=+=+vvvHH

11 22 1 2

()()

Mm m

(13.1.64)

and taking into account (13.1.62), we find

′′

=−vv v

′′

vv v

(13.1.65)

156

′′ ′′

=−vv v

′′ ′′

=+vv v

(13.1.65')

The collision being elastic, the interaction forces are conservative, the potential energy

tending to zero if the distance between the particles tends to infinite (practically, it is

very great), and we can write a conservation theorem of kinetic energy; taking into

account (13.1.65), (13.1.65'), the second relation (13.1.61) takes the form

′′′

+=+

222 2

Mv mv Mv mv , where m is given by (8.1.14). Hence, the relative

velocity is constant in modulus (

′′′

=vv

Observing that the considered mechanical system is closed, the centre of mass

C has

a rectilinear and uniform motion with the velocity

given by (13.1.64) with respect

to an inertial frame of reference; we refer now the motion to an inertial frame

R with

respect to which the centre

C is at rest (the frame

R of the mass centre), using the

index

C (the origin of the frame can be taken even at C ). Because

′′

=+vv v

1CC

′′

=+vvv

2CC

, we can write

′′

=−Hv

m ,

′′

=Hv

m , where we took into

account (13.1.65'); hence,

′′

=−HH

12CC

and, analogously,

′′ ′′

=−HH

12CC

. Finally,

′′′′′′

===

1122CCCC

HHHH (we have

′′′

=vv

), the four momenta having the same

modulus; moreover, we have

′′′

11CC

vv,

′′′

22CC

vv. The angle

θ between the

momenta

′

′′

of the particle

P before and after collision, respectively (the

angle between the directions of motion in

R ) is called diffusion angle (Fig. 13.4).

Fig. 13.4 Diffusion angle

In various experiments, one of the particles (e.g., the particle

P ) represents the

“target”, being at rest with respect to the measuring devices (with respect to the

laboratory); the frame in which we have

′

=v0

will be called the laboratory frame

(denoted by

R ), and the quantities in this frame will be indexed by L. In this case,

from (13.1.64) it results

′

=vv

(/)

mM ; observing that

′′

=−=−vvv v

CCC

we have

′′ ′

=− =− =vv H H

22 1

CC C C

mm, so that

⎛⎞

′′ ′

==+

⎜⎟

⎝⎠

HH H

(13.1.66)

13 Other Considerations on Dynamics of Mechanical Systems

157

MECHANICAL SYSTEMS, CLASSICAL MODELS

After collision, we obtain

′′ ′′ ′′ ′

=+=+HvvHH

111

()

CC C C

(13.1.66')

the recoil momentum of the target being (the conservation theorem of momentum in the

frame

R )

′′′′′′′′

=−=−HHHHH

211

LLL

, (13.1.66'')

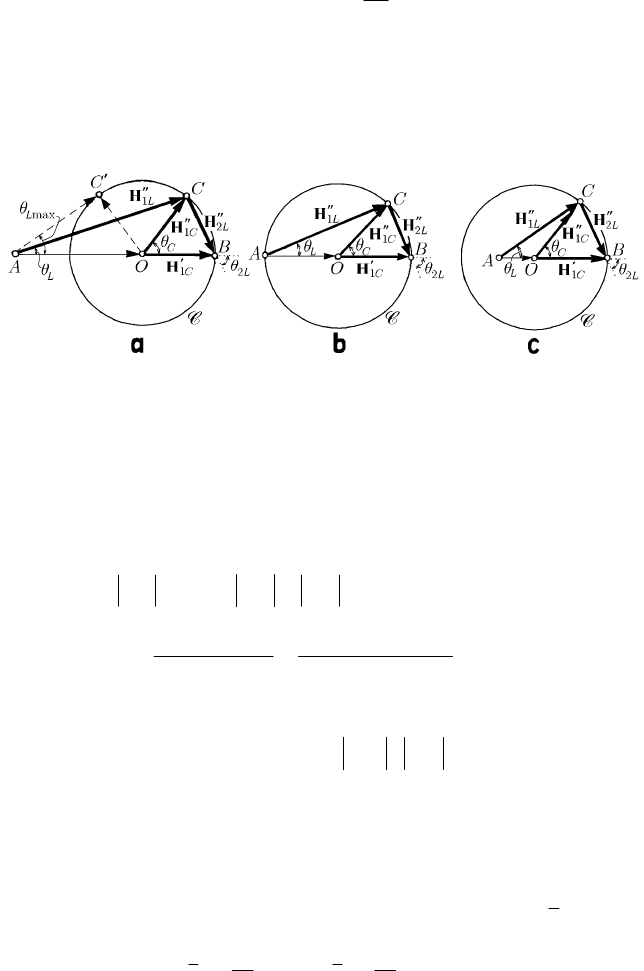
Fig. 13.5 Diffusion angles for: >

mm (a), =

mm (b), <

mm (c)

The relations (13.1.66–13.1.66'') will be geometrically represented in Fig. 13.5a,b,c for

/1mm , =

mm and <

/1mm , respectively. We denote

′

= H





′′

= H





′

= H

(/)

AO m m





and obtain

′

= H





′′

= H





′′

= H





;

the diffusion angles are

and

R and

R , respectively, while the diffusion

angle of the particle “target” is given by

=−

()/2

θπθ. Because we can write the

relation

()

=+tan sin / cos

OC AO OCθθ θ







 

, we obtain

sin tan

tan

cos

1( / )sec

θθ

(13.1.67)

We notice that

[

]

∈ 0,

θπ

. If >

mm, then the point A is outside the circle C so

that

[

]

∈

max

θθ, where

′

max

sin / /

OC AO m mθ









, <

max

θπ

(Fig. 13.5a), while if

mm (Fig. 13.5c), then the point A is inside the circle C, the

angle of diffusion

having the same interval of variation as

; if the particles have

equal masses (

mm), then the point A will be on the circle C, resulting

= /2

θθ (Fig. 13.5b), hence =

max

θπ,

[

]

∈ 0, /2

θπ and +=

θθ π.

In the latter case, we can write the remarkable relations (

′′′

vvv)

′′ ′

cos

′′ ′

sin

(13.1.68)

and after collision the particles move away under a right angle.

158

To can determine the diffusion angles

θ and

θ one must know the law of motion

during the collision of the particles as well as their reciprocal position. We have seen

that the angle

θ has an upper limit if >

mm, while if

mm

we obtain

≅

max

θ , hence ≅ 0

θ ; in this case, after collision with the target, the incidental

particle is practically moving along the same initial direction. If

mm, then the

angle

θ can be anyone, depending essentially on the interaction law and on the initial

conditions, while if

mm

we have ≅

θθ, the “target” particle remaining

practically at rest in

R . In case of a back diffusion ( =−

θθπ), it results

′′ ′

=−HH

11CC

, while the relations (13.1.66') and (13.1.66'') lead us to the momenta

()

′′ ′

=−HH,

′′ ′

=HH

After collision, the kinetic energy of the “target” particle, in the frame

R , will be

(Fig. 13.5)

′′ ′′ ′

==HH

sin

(13.1.69)

while if

θπ

we may write (we use the formula (13.1.66))

′′ ′ ′ ′

== =HH

2max 1 1

LLL

;

(13.1.69')

hence, in case of a back diffusion, the recoil energy (the energy of the “target” particle

after collision) is smaller than (or at the most equal to) the initial kinetic energy of the

incidental particle (which coincides with the initial mechanical energy); indeed,

[

]

=+≤

12 1 2

4/ /( )/2 1mM mm m m . As a matter of fact, this is the maximal

kinetic energy of the “target” particle after collision.

We emphasize that the above results have a general character, non-depending on the

specific interaction law of the two particles. We can thus include in this study also the

case of the “spontaneous” disintegration of a particle in two “fragments” (two particles

which, after disintegration, move independently one of the other). If

′

is the velocity

of the particle before disintegration and

′′

and

′′

are the velocities of one of the

particles resulting from this phenomenon, respectively, then we will have

′′ ′ ′′

=+vvv

, so that

′′ ′ ′ ′′ ′′

+− =

22 2

2cos

LL LL L

vv vv vθ , where

θ is the angle under

which the particle is deviated from the direction of the velocity

′

. If

′′′

vv, then

[

]

∈

max

θθ, with

′′ ′

max

sin /

vvθ . In general,

′′

′′ ′

sin

tan

cos

(13.1.70)

wherefrom

′′

=− ± −

′′

cos sin cos 1 sin

LL L

θθθ θ

;

(13.1.70')

13 Other Considerations on Dynamics of Mechanical Systems

159

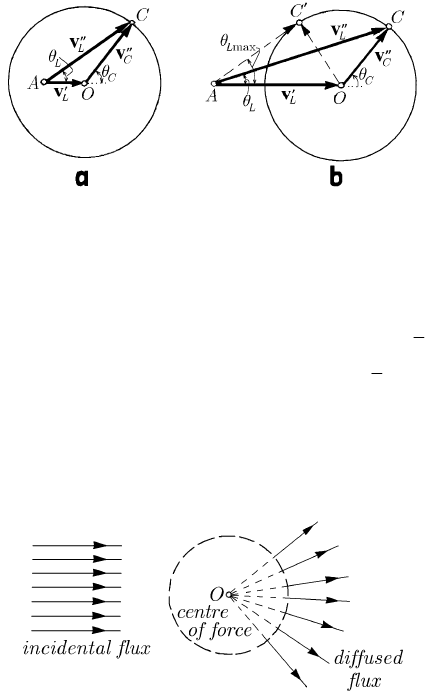
MECHANICAL SYSTEMS, CLASSICAL MODELS

′′ ′

vv (Fig. 13.6a), then one takes the sign + before the radical (the relation is

univocal), if

′′ ′

vv (Fig. 13.6b), then one can take both signs, two solutions being

possible, while in the limit case

′′ ′

vv it results

′′

θθ.

Fig. 13.6 Diffraction angle

In Chap. 8, Sect. 1.2.1, we have considered the problem of deviation of a particle of

mass

m in a field U ( r ) by a fixed centre of force (in the case considered above, it is

situated at the mass centre

C ); the trajectory of the particle is contained between two

asymptotes the angle of which is the diffraction angle

()

=−2πθ∓ (Fig. 8.6), given

by (8.1.17). The parameters which intervene are the velocity

∞

=vv of the incidental

particle at infinity and the collision parameter

b (the distance from the centre of force to

the incidental asymptote of the particle trajectory), the formula (8.1.15) specifying the

constants to be determined. These results complete the problems considered above, by

introducing an interaction law of the two particles (the field

()Ur ).

Fig. 13.7 Phenomenon of diffusion

In general, besides the problem of diffraction (deviation) of a single particle by the

“target”, the problem of diffusion of a great number of particles (flux of particles) by a

centre of force (a field of central forces) is put (Fig. 13.7). Obviously, if the mechanical

phenomenon takes place at an atomic level, then the results which can be obtained in

the frame of a classical model may represent only an approximation (not always the

best one), the quantum effects having an essential importance in this case. Nevertheless,

some results are true, with a good approximation; moreover, the methods used to

describe the diffusion phenomenon are the same in classical as in quantum mechanics.

We will consider an incidental flux of particles which move independently on parallel

rectilinear trajectories, having the same mass

m and the same velocity

∞

v (a

160

homogeneous incidental beam of particles, which can be electrons, particles or celestial

bodies). Passing in the vicinity of the centre of force

O, the particles are influenced by

that one; being diffused with velocities in various directions, but of the same magnitude

(elastic diffusion) and becoming again independent. To this goal, the centre of force

must have a finite radius of action; hence, one must have

≠() 0Ur for <

rr and

=() 0Ur for >

rr. Practically, it is sufficient to have

→∞

=lim ( ) 0

; in this case,

=−>0ETU because =>0ET at infinity. The trajectories of the particles are

curves symmetric with respect to the straight line which passes through

O and through

the pericentre

P (see Fig. 8.6). The diffusion angle  is the angle made by the two

asymptotes of the trajectory and is the same for all the particles which have the same

collision parameter

b. To can evaluate the way in which the particles having a collision

parameter contained in a certain interval are deviated in directions contained, as well, in

a given interval, one defines the efficacious (differential) section of diffusion

dσ in the

form

(13.1.71)

Fig. 13.8 Efficacious section of diffusion

where

dN is the number of particles diffused in the solid angle dω in a unity of time,

while

n is the number of incident particles which cross the unit area in the same time;

this ratio constitutes the most important characteristic of the process of diffusion.

Assuming that between  and

b there exists a one-to-one correspondence, hence that

the function

= ()b is a monotone decreasing function, the only particles diffused

in the interval

[

]

+,d 

are those the collision parameter of which is contained

between

()b  and +() d()bb; the number of these particles will be, obviously,

=d2dNbbnπ , resulting the efficacious section (an annular section, the phenomenon

being with axial symmetry with respect to the

Ox-axis (Fig. 13.8)

=d2dbbσπ

. (13.1.71')

The relation between the efficacious section of diffusion and the diffusion angle (plane

angle) will result in the form

13 Other Considerations on Dynamics of Mechanical Systems

161

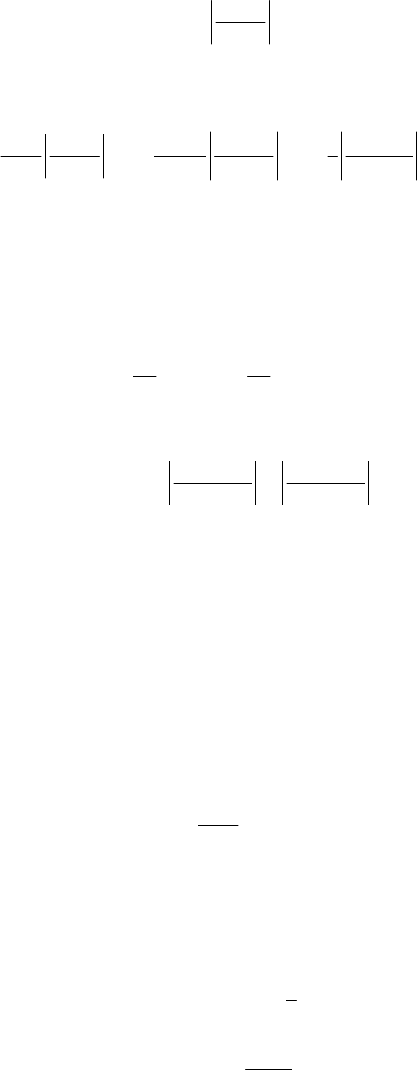
MECHANICAL SYSTEMS, CLASSICAL MODELS

d( )

d2() d

bσπ







(13.1.71'')

where the derivative is taken in absolute value because, in general, it is negative. With

reference to the element of solid angle

=d2sindωπ, we obtain

== =

()d() d () d()

dd dd

sin d 2sin d 2

d(cos )

bb b b

σω ωω

  



(13.1.71''')

If the diffusion of the beam of particles is not due to a fixed centre of force and to other

particles which are initially at rest, then it results that the formulae (13.1.71''),

(13.1.71''') take place in the frame

R . Passing to the frame

R , the efficacious

section

dσ is not modified (it is defined as a ratio of numbers of particles, being

independent of frame), but the element of solid angle is modified, so that

() ()

dd d

σσ

σω ω

ωω

;

(13.1.72)

we notice that

d(cos ) d(cos )

d2sind d

d(cos ) d(cos )

CC C

ωπ ω



(13.1.72')

so that, taking into account (13.1.67) too, we can make a calculus in the frame

R .

In the case of a diffusion on the “spherical potential hollow”, for which

≤

⎧

⎪

⎨

⎪

⎩

for ,

()

0 for ,

UrR

(13.1.73)

where

U is a positive constant, we get

Rσπ

, hence the area of the central section

of the sphere.

In particular, we consider the diffusion of a beam of particles of charge

q on the

“target” formed by the particles of charge

q , in a potential field (9.2.4), with

πε

(13.1.74)

ε being the permittivity of vacuum in a rationalized system. The diffusion angle is

given by

sin( /2) 1/e= , where 1e > is the eccentricity of the trajectory of a

particle of charge

q (the trajectories are hyperbolae, as in case of the deviation of the

luminous radius, so that we can use the formula (9.2.27'')). Replacing the constants

and

k given by (8.1.15) and (9.2.5), we obtain (vv

∞

= )

mv b

∞

⎛⎞

⎜⎟

⎝⎠

162