Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

If the relative velocity of the centre of mass

C (with respect to the frame R ) is non-

zero (

≠v0

), then the absolute velocity (with respect to the frame

′

) of this centre

is given by

CCC

′′

=+vvv

(13.2.5')

so that

()

′′

=−Hvv

;

(13.2.6')

it results that the absolute velocity of the centre of mass

C is equal to its relative

velocity if the momentum of the mechanical system

S with respect to the fixed frame

vanishes (

′

=H0

We assume, to fix the ideas, that the emission phenomenon of some elements of the

particles

P , 1,2,...,jn= , of relative velocities (with respect to these particles)

′

=−wuv

, 1,2,...,jn= ,

(13.2.7)

where

u are the velocities of these elements with respect to the frame

′

R . In this

case, the equation (10.3.1') allows to write

()

ii i ii

′

=+ +

∑



vF F u

m <



where

F is the resultant of the given external forces which are applied upon the

particle

P , while

F are the internal forces due to the action of the particles

P ;

summing for all the particles of the discrete mechanical system

S and observing that

the resultant of the internal forces vanishes, we obtain

′

∑



HR u, 0

m <



(13.2.8)

stating

Theorem 3.2.1 (theorem of momentum). The derivative with respect to time of the

momentum of a free discrete mechanical system of variable mass (which emits mass),

with respect to an inertial frame of reference, at a given moment, is equal to the sum of

the resultant of the given external forces which act upon that system and the momentum

of the emitted masses in a unity of time, at that moment.

Taking into account (13.2.7), we can write the relation (13.2.8) in the form

′′

=++

∑



HR vR , 0

m <



(13.2.8')

13 Other Considerations on Dynamics of Mechanical Systems

173

MECHANICAL SYSTEMS, CLASSICAL MODELS

too, where

()

jj jj

′

=−=

∑∑



uv wR

, 0

m <



(13.2.9)

is the resultant of the reactive forces; we mention, as well (for the particles which do

not emit mass we have

m =



), a theorem of the dynamic resultant in the form

ii ii

′′ ′

===+

∑∑



AavRR

(13.2.8'')

where

′

is the dynamic resultant of the discrete mechanical system S.

If the absolute velocities of the emitted elements vanish (

=u0, 1,2,...,jn= ),

then the relation (13.2.8) is written in the form

′



(13.2.8''')

hence in the same form as in case of a discrete mechanical system of constant mass; as

well, if the relative velocities of the emitted elements are zero (

=w0,

1,2,...,jn= ), then R = 0, while the relation (13.2.8'') takes the classical form

′

=AR

(13.2.8

)

These cases have been considered by T. Levi-Civita.

Taking into account (13.2.4'), we notice that

[]

()

mM M

′′ ′

=+×+××=

∑



va aωρ ω ωρ

so that

′

=+aR

R ;

(13.2.10)

we thus state

Theorem 13.2.2 (theorem of motion of the centre of mass). The point which coincides

with the centre of mass of a free discrete mechanical system of variable mass (which

emits mass) moves, at a given moment, with respect to an inertial frame of reference, as

a particle of constant mass, at which would be concentrated the whole mass of the

system at that moment and which would be acted upon by the sum of the resultant of the

given external forces and the resultant of the reactive forces.

This equation takes into account that the centre of mass

C changes the position with

respect to the frame

R, due to the variation of the mass of the mechanical system S. As

a matter of fact, the acceleration

′

is the transportation acceleration; taking into

account the relative motion, we have

174

CCC C

′′

=++×aaa vω

(13.2.11)

where

a and 2

× vω are the relative acceleration and the Coriolis acceleration,

respectively, corresponding to the mass centre

C. We obtain thus the equation

CCC

MMM

′

=++ + ×aR a vω

R ,

(13.2.10')

which governs the motion of the mass centre of the discrete mechanical system

S with

respect to an inertial frame of reference.

In case of a discrete mechanical system of variable mass, which captures mass, we

obtain – analogously – a relation of the form (13.2.8), but for which

m >



, and we

can state a theorem of momentum and a theorem of motion of the mass centre in the

same form. We may develop a unitary theory too, starting from Meshcherskiĭ’s

generalized equation, in the form (10.3.8) or in the form (13.2.1). We find thus the

theorem of momentum

jjj

−− ++

′

=+ +

∑∑





HR u u

(13.2.12)

as well as the theorem of the dynamic resultant

−

′′

==++

∑



AvRR R

(13.2.12')

where we have introduced the reactive force

()

jj jj

−− −−

−

′

=−=

∑∑



uv wR

(13.2.13)

and the braking force

()

jj jj

++ ++

′

=−=

∑∑



uv wR

;

(13.2.13')

the used notations correspond to the previous ones; we suppose that there are

nn≤

particles which emit and capture mass (eventually, some of those particles can only emit

or only capture mass, having

j jjj

mmmm

−+

=++,

−



, correspond-

ing to the notation (10.3.11)). The theorem of motion of the mass centre becomes

−

′

=+ +aR

RR,

(13.2.12'')

where

M is the mass of the discrete mechanical system S at a given moment.

13 Other Considerations on Dynamics of Mechanical Systems

175

MECHANICAL SYSTEMS, CLASSICAL MODELS

The moment of momentum of the discrete mechanical system

S of variable mass

will be defined in the form

() ( )( )

iii i i i

′

′′′ ′ ′

=× = +×+×

∑∑

Krv rrv rω

so that, corresponding to the formula (11.2.16), we obtain

() ()

OC O

′

′′′ ′

=+× +×KKr v vρ

(13.2.14)

where the pseudomoment of momentum

is given by

()

ii i

=××=

∑

KrrIωω

OC≡

, hence if ρ = 0, then we obtain a formula of Koenig type of the form

(11.2.21). Introducing the frame

R with the axes parallel to those of the frame

′

R ,

we have

=KK too.

We can write

() ' ()

iiiiii iii

′′′′ ′

×=×+×+×

∑



rvrFrFru, 0

m <



for a particle

P , assuming – to fix the ideas – that only a phenomenon of emission

takes place. Summing for all the particles of the discrete mechanical system

S and

observing that the resultant moment of the inertial forces is equal to zero, it results

()

′′

=+ ×

∑



KM r u

, 0

m <



(13.2.15)

and we can state

Theorem 13.2.3 (theorem of moment of momentum). The derivative with respect to time

of the moment of momentum of a free discrete mechanical system of variable mass

(which emits mass), with respect to a fixed pole, in an inertial frame of reference, at a

given moment, is equal to the sum of the resultant moment of the given external forces

which act upon that system, with respect to the same pole, and the moment of

momentum of the emitted masses in a unity of time at that moment, with respect to the

mentioned pole.

Taking into account (13.2.7), we can also write

()

OOO

′′′

=++ ×

∑



KM r vM , 0

m <



(13.2.15')

where

176

()

′

=×

∑



rwM , 0

m <



(13.2.16)

is the resultant moment of the reactive forces with respect to the fixed pole

′

. If the

absolute velocities of the emitted masses vanish (

=u0, j = 1,2,…,n), the relation

(13.2.15) is written in the form

′′

′



KM;

(13.2.15'')

hence, in the case considered by Levi-Civita, one obtains the same form as in the case

of a discrete mechanical system of constant mass.

Proceeding as in Sect. 11.2.2.1, we can find for the theorem of moment of momentum

an analogue of the formula (11.2.18), in the form (given by C. Agostinelli)

()() ()

OOOO

′′′

×+ =++×

∑



aIM rvρωM , 0

m <



(13.2.15''')

In case of capture of mass, we obtain the same formulae (13.2.15

−13.2.16), where

m >



. Analogously, we obtain results corresponding to the generalized equation

(10.3.8) of Meshcherskiĭ.

We notice that we can group the theorem of momentum and the theorem of moment

of momentum, hence the formulae (13.2.8), (13.2.15) in the form of a theorem of

kinetic torsor; thus, it results

{} {} {}

{}

iiijj

OOOO

′′′′

τ=τ=τ+τ



HHFu.

(13.2.17)

13.2.1.3 Theorem of Kinetic Energy

The kinetic energy of the discrete mechanical system

S of variable mass is defined in

the form

()

ii i

Tv m

′′ ′

== +×

∑∑

vrω

;

corresponding to the formula (11.2.28), we get

(,,)

TT Mv M

′′′

=+ +v ω

(13.2.18)

where the pseudokinetic energy

T is given by

() ()

=×=⋅

∑

rIωωω

(13.2.18')

13 Other Considerations on Dynamics of Mechanical Systems

177

MECHANICAL SYSTEMS, CLASSICAL MODELS

OC≡ , hence if ρ = 0, then we obtain a formula of Koenig type of the form

(11.2.37). By introducing the frame

R , we may write

TT= too.

Starting from the equation of motion of a single particle and effecting a scalar

product by

′′

=vr

, we can write

d( ) d ' d d

iiiii iiii

′′ ′ ′ ′

⋅ =⋅+ ⋅+ ⋅

∑

vvFrFruv

, 0

m <



where – to fix the ideas – we have admitted that a phenomenon of emission takes place.

We notice that

()

d( ) d d

iii ii ii

mm m

′′ ′′

⋅= +vv vv

and

dd()dd d d

ii i i i i i ii i i i ii i i i

mm mvm mvm

′′′′′′′

⋅= + ⋅= + ⋅= + ⋅



uv w v v wv w r.

Summing for all the particles of the discrete mechanical system

S, it results

int

ddd d d

TWW W mv

′′

=+ + +

∑

, 0

m <



(13.2.19)

where we have introduced the elementary work of the reactive forces in the form

d()d

′

=⋅

∑



, 0

m <



;

(13.2.20)

we state thus

Theorem 13.2.4 (theorem of kinetic energy). The differential of the kinetic energy of a

free discrete mechanical system of variable mass (which emits mass), in an inertial

frame of reference, at a given moment

t, is equal to the sum of the elementary work of

the given external and internal forces which act upon that system, the work of the

reactive forces at the same moment and the kinetic energy of the masses emitted in the

interval of time dt.

The formulae (13.2.19), (13.2.20) hold also in case of capture of mass (we have

m >



); as well, starting from Meshcherskiĭ’s generalized equation (10.3.8), we

obtain analogous results.

In the particular case considered by Levi-Civita, in which the absolute velocities of

the emitted (or captured) masses vanish (

=u0, 1,2,...,jn= ), we can write

int int

ddd d dd d

TWW W WW m

′′

=+ + =+ −

∑

;

(13.2.19')

178

but if the relative velocities of the emitted masses are null (case considered by Levi-

Civita), then we obtain (we have

d0W =

)

int

ddd d

TWW m

′′

=+ +

∑

v .

(13.2.19'')

13.2.2 Applications

In what follows, we deal firstly with the problem of the rocket; we consider then the

problem of

n particles and, in particular, the cases 2n = , and 3n = , including the

problem of motion of an artificial celestial body.

13.2.2.1 The Rocket Problem

In case of a rocket, elements of mass of its body are emitted, hence

m <



1,2,...,jn= ; we assume that the relative velocity

w is the same (equal to w) for all

the emitted masses. Among the external forces which act upon the rocket we will render

evident the pressures

p, of resultant

R and resultant moment

, exerted on the

walls by the surrounding air. The theorem of motion of the mass centre and the theorem

of moment of momentum are written in the form

[

]

()

′

+×+× × = + +



aRRwωρ ω ωρ , 0M <



(13.2.21)

()

()()

OOO

′

×+ =++×



aIMM wρωρ

()

jjj

′′

+×+×

∑∑



rwrv

, 0

m <



(13.2.21')

where we took into account that

()C

=+rrρ . The moment of the reactive force with

respect to the mass centre

C of the emitted masses can be neglected, assuming that (the

emitted mass is much smaller than the mass of the rocket)

() ()

∑



r0ρ

;

as well, on the basis of the same considerations, we have

()

jjj

′′′′

×=×

∑



rv vρ ,

where

′

is the absolute velocity of the rocket. The equation (13.2.21') becomes thus

() ()

()()

OOO

MMM

′′′

×+ =++×+×



aIMM w vρωρρ.

(13.2.21'')

13 Other Considerations on Dynamics of Mechanical Systems

179

MECHANICAL SYSTEMS, CLASSICAL MODELS

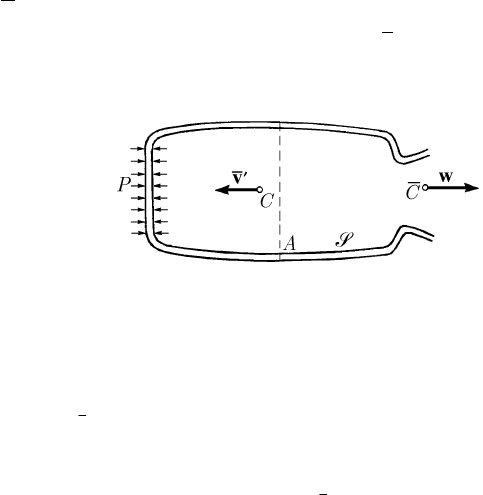
Hence, in the equations of motion of the rocket (the mechanical system

S ) one introduces

the influence of the air pressure and of the reactive force, considered as applied at the mass

centre

C of the emitted masses (Fig. 13.9); in the corresponding equation of the moment

of momentum appears also the moment of the force

′



v , with respect to the pole O

′

an inertial frame of reference (with respect to which one calculates the acceleration

′

too and in which the differentiation with respect to time is performed).

Fig. 13.9 Rocket problem

In this problem, the acceleration

()

′′

aa and the angular velocity ()t=ωω

must be determined, supposing that the law of variation of mass

()MMt= , deduced

from the law of combustion of fuel, is known. Due to the emission of mass, the position

vectors

ρ and

, as well as the moment of inertia tensor

, are functions of time;

their variation depends on the mass and on the position of the eliminated elements.

Hence, one must assume that the laws of variation of those quantities are given too. In a

first approximation, we can consider that

ρ,

and

I are constant quantities, at least

for a short time interval. We mention that the torsor

{

}

RM of the hydrodynamic

forces corresponds to the pressure of the air, exerted on the external walls of the rocket

(a mechanical system

S of variable mass immersed in a fluid), as well as to the

pressure of the gases resulting from explosions (on the internal surface of the rocket);

thus, there intervene also problems of dynamics of gases, of thermodynamics and even

of interactions between the rocket and gases. All these aspects complicate much the

problem of the rocket from the mathematical point of view; we assume thus that the

action of the pressure is known in time. In this order of ideas, we consider that the

rocket can be modelled mathematically as a particle of variable mass.

Let be thus a rocket launched at the Earth surface, at the initial moment, the motion

taking place along the local vertical (the

Ox-axis is along the ascendent vertical; see

Fig. 10.22 too). In the active phase (the rocket moves due to the action of the fuel), the

equation (13.2.21) allows to write (the relative velocity

w is directed opposite to the

velocity

v, hence its component along the Ox-axis is −w; the reactive force R has the

same direction as the velocity

v, because 0M <



)

()Mv Mw M g vϕ=− −



(13.2.22)

where

()Mg vϕ is the resistance of the air (corresponding to the pressure) and where

we consider a linear law of variation of mass (

(1 )MM tα=−,

constα =

180

We assume that

() (/)vkgvϕ = , with

kCA Mμ= , where A is the area of the

maximal cross section of the rocket,

μμ

−

const

μ =

constβ =

, is the

unit mass of the air, while

C is a non-dimensional coefficient of resistance. We notice

that

()wuv−=− −, where constu−= is the absolute velocity of gases’ elimination;

the equation (13.2.22) becomes

(1 ) e

tx x k x u

αα α

−

−−+ =

  

(13.2.22')

having a quite complicated non-linear form.

An essential simplification of the problem is obtained by neglecting the resistance of

the air; we find thus again Tsiolkovskiĭ’s first problem (see Chap. 10, Sect. 3.1.4 too),

with the hypothesis

constwuv=−≠ . The equation of motion takes the form

(1 ) ( )tv v uαα−=+



(13.2.23)

wherefrom we get

()

vt v

−

(13.2.23')

where

(0)vv= is the initial velocity. By a new integration, we can write

(

(0)xx= )

() ( ) ln(1 )

xt x u v t t

=−− − − .

(13.2.23'')

Another simplification of the problem can be obtained by adjustment of the law of

combustion, so that the rocket have a uniform accelerated motion along the ascendent

vertical; the velocity

v of the mass centre of the rocket will be thus given by

2vax=

, with the acceleration

constva==



. In its motion, the rocket must

overcome the resistance of the air

()Mg vϕ and the force of attraction of the Earth

Mm r , rRx=+, where

m is the Earth’s mass and we have

mgR= , R

being the radius of the Earth, considered to be spherical, while

g is the gravity

acceleration. In this case, the elementary work corresponding to the displacement along

the ascendent vertical is given by

()

ded

WMg Kx x

β−

⎡ ⎤

⎢ ⎥

⎣ ⎦

where

KaACμ= is a constant. Integrating between the limits 0 and H, we obtain

the work effected by rising the rocket at the height

H in the form

1(1 )e

MgRH

−

=+−−

⎡

⎤

⎣

⎦

;

(13.2.24)

13 Other Considerations on Dynamics of Mechanical Systems

181

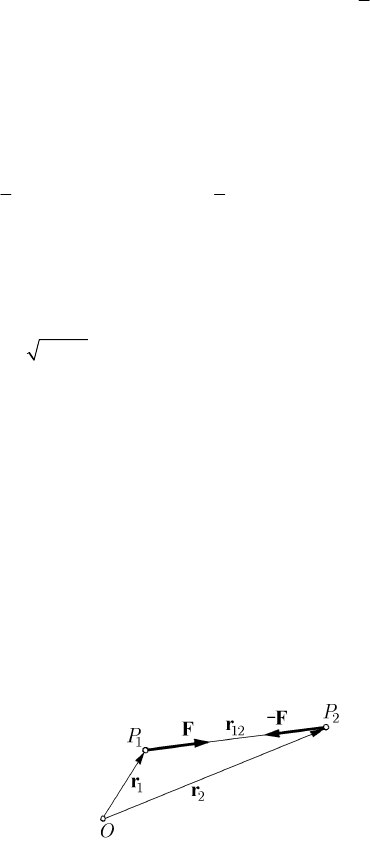
MECHANICAL SYSTEMS, CLASSICAL MODELS

because we do not know the law of motion

()xxt= (we cannot express the mass as a

function of

x), we will introduce a mean mass

MMMM−Δ < < , where 0MΔ>

is the lost mass of the rocket at the height H. If

10 cmβ

−−

= , for

350km 3.5 10 cmH ==⋅, then we have

(1 )e 36e

−−

2.270 10

−

≅⋅

1 . Assuming that

10 9.81 10 cm/sag=≅⋅

242

1 m 10 cmA = =

033

10 g/cm

−

= , 6C = , it results

1.177 10 g/sK ≅⋅ , while

21822

/1.17710gcm/sK β ≅⋅⋅ ; with

9.81 10 cm/sg =⋅ ,

6.38 10 cmR =⋅ and

supposing that

510gM =⋅ , we have

17 2 2

/( ) 1.627 10 g cm /sMgRH R H+≅ ⋅ ⋅ .

Finally, we obtain

18 2 2 18 11

1.340 10 g cm /s 1.340 10 erg 1.340 10 JW =⋅⋅ =⋅ =⋅,

hence the approximate value of the mechanical energy necessary for the rocket to come

out from the terrestrial atmosphere (these data are important to design the motor of the

rocket); we notice also that

/WKβ≅ (with an error of 12% in the preceding case).

The velocity

2 8.287 10 cm/s 8.287 km/sVaH=≅⋅ = at the height H, is

reached after an interval of time

/ 84.48 sTVa==; the velocity V is thus greater

than the first cosmic velocity at the height

H (smaller than at the Earth surface, as it was

shown in Chap. 9, Sect. 2.2.2). The duration

T is, in fact, greater, the trajectory of the

rocket being – in reality – curvilinear; in practice, the active phase is of several minutes.

13.2.2.2 Problem of n Particles

We shall study the problem of

n particles in the case of the capture phenomenon; we

assume thus, for instance, that one has to do with celestial bodies acted upon by internal

forces of Newtonian attraction, which are capturing meteorites. We consider to be in the

Levi-Civita case (the absolute velocity of the captured masses vanishes), the equation of

motion of a particle being of the form (10.3.4).

Fig. 13.10 Problem of two particles

In the case

n = 2 (the problem of two particles), studied in 1928, in the frame of the

mentioned mathematical model, by Gh. Vrănceanu, let

and

be two particles of

position vectors

r and

r , with respect to an inertial frame of reference, and of

variable masses

m and

m , respectively; we denote

12 2 1

=−rrr (Fig. 13.10), the

force of universal attraction (conservative force, which derives from the potential

182