Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

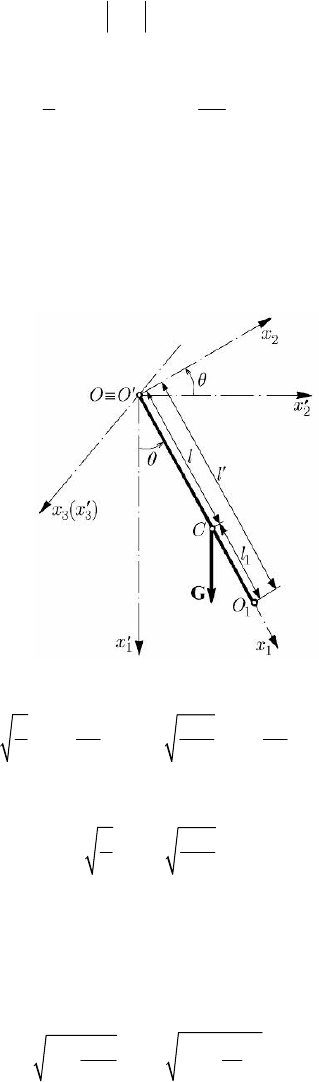
= ()tθθ (Fig. 14.7). Denoting =OC l





and observing that =GgM , we get

=−

sin

MMglθ ; we can thus write the equation of motion (14.2.2) in the form

′

sin 0

θθ



′

(14.2.6)

We find again the equation (7.1.38') of a simple pendulum of equivalent length

′

called the synchronous simple pendulum of the considered physical pendulum;

imposing the same initial conditions, the motions of the two pendulums will be

specified by the same function

= ()tθθ , so that one can use all the results obtained in

Chap. 7, Subsec. 1.3.1. In case of great oscillations, we use the formula (7.1.43'') which,

with a good approximation, leads to the period

′

⎛⎞ ⎛⎞

=+= +

⎜⎟ ⎜⎟

⎝⎠ ⎝⎠

21 2 1

16 16

gMgl

αα

ππ

(14.2.7)

where

max

αθ ; in case of isochronous (small) oscillations, we can write

′

gMgl

ππ.

(14.2.7')

The Huygens-Steiner theorem, expressed by the formula (3.1.113), allows to write

IIMl

, where

I is the moment of inertia of the physical pendulum with

respect to an axis parallel to the horizontal

′′

Ox -axis, passing through the mass centre

C. If we denote by

T the period of the simple pendulum of length l, then it results

()

=+=+

TT T

(14.2.7'')

Fig. 14.7 Physical pendulum

243

14 Dynamics of the Rigid Solid

where

= /

iIM is the central radius of gyration, defined by the relation (3.1.30),

corresponding to the same axis which passes through C. Thus, we can write

′

lll, ==

Ml l

(14.2.8)

A point

O on the axis

Ox is defined so that

OO l l

′

=>, the centre of mass C

being contained between the point O, called centre of suspension, and the point

O ,

called centre of oscillation (Fig. 14.7). A particle situated at the point

has the same

motion as the synchronous simple pendulum. The horizontal axes parallel to the axis

′′

Ox , which pass through the points O and

O are called axis of suspension and axis of

oscillation, respectively. If we maintain the direction of the horizontal axis

′′

(hence, the quantities

and

), as well as the distance from the centre of mass C to

the centre of suspension O, the length

′

of the synchronous simple pendulum remains

invariant; we can thus state that all the generatrices of a circular cylinder the axis of

which is horizontal and passes through the mass centre lead to physical pendulums

which, in the same initial conditions, have identical motions. If we maintain constant

only the axis of suspension, the length

′

depends on the distance l. The graphic of the

function

′′

= ()lll

is a branch of a hyperbola contained in the second octant of the

plane (Fig. 14.8); we notice that for

li we get

′

min

lil.

Assuming that the axis of suspension is a principal axis of inertia (e.g., in case of a

geometrical and mechanical symmetry with respect to the

Ox x

-plane, we have

23 31

0II

) and observing that

, it results that this one is a

permanent axis of rotation too (in a large sense, with

≠

); hence, it is sufficient

only one point of support for the axis, having only one constraint force at

′

≡OO

, the

components of which are given by (14.2.5) in the form

Fig. 14.8 Diagram of l

′

vs l in case of a physical pendulum

244

MECHANICAL SYSTEMS, CLASSICAL MODELS

()

′

=− +

cosRMg lθω,

()

′

=− +

cosRMg lθω



′

0R ,

(14.2.9)

and which is situated in the

Ox x -plane. Starting from the equation (14.2.6), which we

multiply by

=θω



, we obtain

′

cos

, =−

′

cos

(14.2.9')

where we take into account the initial conditions

()

tθθ,

()

tωω; finally, we

can write

cos 2

RMg CMl

′

=− −

′

sin

RMg

′

0R .

(14.2.9'')

Hence, the constraint forces are periodical functions of time with the period T; the

component

′

R does not depend on the initial conditions, being directed in the sense of

the motion (

′

R has the same sign as

sinθ

, hence as θ), but the component

′

R depends

on these conditions, being always directed in the opposite sense to that in which is the

mass centre (

′

0R ).

If the angular velocity

=ωθ



maintains its sign, then the motion is circular and the

pendulum is rotating in the same sense. From (14.2.9') we notice that, to have such a

motion, it is necessary and sufficient that

′

> /Cgl

, wherefrom

2cos

;

(14.2.10)

the initial angular velocity (considered to be positive) must be greater than a given

value, depending on the initial conditions (angle

θ ) too. Such a situation is

encountered, e.g., in case of a fly wheel, the axle of which (assumed to be horizontal)

does not pass exactly through the mass centre, but at a short distance to that one; the

phenomenon of resonance (the frequency of the perturbing constraint force is close to

the frequency of the proper vibration), which leads to a critical rotation speed, must be

avoid.

From the equation (14.2.6) it results that the physical pendulum is at rest with respect

to the inertial frame of reference

′

R if =

sin 0θ , where

θ corresponds to the initial

position (at the moment

); it results that

0θ

θπ

, the centre of mass C

being situated on the vertical of the centre of suspension. Obviously, only the position

0θ is a stable position of equilibrium; in this case =() 0tθ and

===

() () 0ttθωω



We have seen that the centre of oscillation is at a distance

′

>ll

(we can have an

equality only if

= 0

i , hence only if the rigid solid is reduced to a particle or to a

material segment of a line, parallel to the axis of suspension) of the suspension centre;

245

14 Dynamics of the Rigid Solid

Huygens showed that all the points of the axis of oscillation move as they would be

mathematical pendulums connected to the axis of suspension by inextensible threads of

length

′

The second relation (14.2.8) can be written also in the form

ll i

(14.2.11)

This allows to state

Theorem 14.2.3 (Huygens) The suspension and oscillation axes of a physical

pendulum are reciprocal.

This property with an involutive character shows that if one takes the axis of

oscillation as axis of suspension, then the axis of suspension becomes an axis of

oscillation.

Fig. 14.9. Huygens’s theorem

The relation (14.2.8) can be written in the form of an equation of second degree

′

−+ =

llli ,

(14.2.12)

of roots (for given

′

and

i correspond two values for l)

()

⎡

⎤

′

′′

=±− =±−

⎢

⎥

′

⎣

⎦

1,2

411

llli

(14.2.12')

We can thus state

Theorem 14.2.4 (Huygens) The locus of the straight lines of given direction, which –

taken as axes of suspension – allow to a physical pendulum to oscillate about them with

a given period is formed by two circular cylinders (the common axis of which passes

through the mass centre and has the given direction).

The period T being given, it results that the length

′

of the synchronous simple

pendulum is, as well, given. Assuming that

′

> 2

li, the formula (14.2.12') gives the

lengths

l and

l of the radii of the two cylinders; if

′′

min

lil (corresponding to

Fig. 14.8), then the two cylinders coincide (

′

== =

12min

lll i).

246

MECHANICAL SYSTEMS, CLASSICAL MODELS

Observing that

ll i , it results ≥

li and ≤

li (or conversely); as well, we

have

′

ll l. If the centre of suspension

O corresponds to the centre of

oscillation

′

, = 1, 2i , and if we assume that these centres are coplanar with the

centre of mass C, so that the points

O and

′

O and the points

O and

′

O ,

respectively, be on the same arcs of circle (Fig. 14.9), the Theorem 14.2.4 leads to

Theorem 14.2.4' (Huygens) If two parallel axes of suspension of a physical pendulum

lead to the same length for the corresponding synchronous simple pendulums, then this

length is equal to the sum of the distances from the mass centre to the two axes.

This theorem is justified for the relation of order

≤≤

li l

. In the particular case

in which the two axes of suspension are coplanar with the mass centre, we find again

the Theorem 14.2.3.

The theory of the physical pendulum allows an experimental determination of the

moment of inertia of a rigid solid with respect to a given axis, which pierces this solid.

To do this, one takes the respective axis as axis of suspension and one measures the

isochronous oscillation period of the rigid solid, in its behaviour as a physical

pendulum; knowing the own weight of the rigid solid (the mass and the gravity

acceleration) and the distance from the centre of mass to the considered axis, the

formula (14.2.7') gives the possibility to compute the axial moment of inertia in the

form

()

IMglMgl

(14.2.13)

Because the quantities M and I cannot be measured with a sufficient precision, one

resorts to experimental artificial means. A rigid mass

M uniformly distributed around

the axis of suspension is added, so that its centre of mass be on this axis, the

corresponding moment of inertia being

I . Obviously, we have

()

+= +

II MMgl

Taking into account the relation of static moments

()

+=MMlMl and the relation

(14.2.13), we obtain

()

−−

33 33

II I

TT TT

(14.2.14)

Knowing the moment of inertia

I and measuring the periods T and

, we get the

moment of inertia

I with a sufficient good precision.

14.2.1.3 Experimental Determination of Moments of Inertia of Rigid Solids

247

14 Dynamics of the Rigid Solid

e Gravity Acceleration. The Borda, the

Kater and the Bessel Pendulums

The physical pendulum and the formula (14.2.7') of its isochronous oscillations

allow, as well, to determine experimentally the gravity acceleration; we get thus

()

⎡

⎤

′

== = +

⎢

⎥

⎣

⎦

22 2

44 4

gl l

Ml l

TT T

ππ π

(14.2.15)

We assume that in this formula are known or measurable all the quantities, so that it is

possible to obtain g. In 1792, Borda used a physical pendulum formed by a

homogeneous sphere of platinum, suspended by a thin metallic thread, of negligible

mass with respect to the mass of the sphere; the mass centre C of the physical

pendulum is thus practically situated at the centre of the sphere of radius R and mass

M . The formula (3.1.27) leads to the central radius of gyration

= 2/5

iR. If l is the

distance from the centre of suspension to the centre of the sphere and if we determine

experimentally the period T of the isochronous oscillations, then we obtain the

acceleration g of gravity. We notice that, to have a result with the best precision, one

must take into account the influence of the medium (temperature correction, reduction

to vacuum, resistance of the air etc.), the influence of the suspension (the curvature of

the supporting blade edge, the displacement of the support, the friction on the axle etc.)

and the influence of the experimental measurements (the measure of the distance

=lOC and the measure of the period T of the isochronous oscillations).

The period of oscillation of the pendulum is obtained by one of the known

experimental methods (e.g., the method of simultaneousness or the method of

registering); the use of the formula (14.2.15) corresponds to an absolute determination

of the gravity constant g. A rigorous determination being particularly difficult, as we

have seen, one obtains such results only in gravimetrical stations of reference (such

stations are, e.g., these of Potsdam and Helsinki). In other stations one obtains relative

determinations, starting from the determinations

T and

g in a station of reference,

using an identical physical pendulum, in the same conditions (to have the same length

′

of the synchronous simple pendulum),

()

(14.2.16)

The gravity acceleration g is thus obtained by a simple measurement of the period T.

If in the Theorem 14.2.4' the plane of the axes of suspension contains the centre of

mass C too, so that the latter one be situated between the points

O and

O (in this

case

′

≡

OO), then the length of the synchronous simple pendulum is equal to the

distance between the two axes; the respective pendulum is a reversible pendulum,

14.2.1.4 Experimental Determination of th

248

MECHANICAL SYSTEMS, CLASSICAL MODELS

allowing the determination of the centre of oscillation and of the length

′

lll.

Such a pendulum was built for the first time in 1818 by H. Kater from a bar of bronze,

along which glide two masses

m and

m , with the aid of a micrometric screw, and

which has two centres of suspension

O and

O , with two blades; thus, by the

displacement of the mass centre C, one can make one of the centres of suspension to

become centre of oscillation for the other one, and reciprocally. In fact, one obtains

⎛⎞

⎜⎟

⎝⎠

⎛⎞

⎜⎟

⎝⎠

where

i must be the same in the two expressions, till an experimental error;

eliminating the central radius of gyration, it results

()

−

′

== +=

−

11 22

Tl Tl

Tl ll

gg ll

ππ

, ≠

ll,

(14.2.17)

wherefrom

()

22 2 2

111

12 1 12 1

1 1 1 ...

lT l T

TT T T

ll T ll T

⎡⎤ ⎡⎤

⎛⎞ ⎛⎞

=+ − =+ − +

⎜⎟ ⎜⎟

⎢⎥ ⎢⎥

−−

⎝⎠ ⎝⎠

⎣⎦ ⎣⎦

(14.2.17')

Hence, the passing from a centre of suspension to another one leads to a term of

correction applied to the period noticed in case of the first axis of suspension. From

(14.2.17) we obtain also

−

11 22

Tl Tl

π .

(14.2.17'')

This formula is much used in geodesy to determine experimentally the gravity

acceleration by two measurements of periods corresponding to two axes of suspension.

Fig. 14.10 Bessel’s pendulum

249

14 Dynamics of the Rigid Solid

Making

−→

0TT and taking into account the Theorem 14.2.4', we find again the

formula (14.2.15).

If the masses

m and

m have a different form, then one obtains experimental

errors due to a different resistance of the air. To eliminate these errors, Bessel

considered a physical pendulum for which the masses

m and

m have the same form

and the same dimension, but different masses (a hollow cylinder and a full one)

(Fig. 14.10).

One has used physical pendulums of various forms to determine the gravity

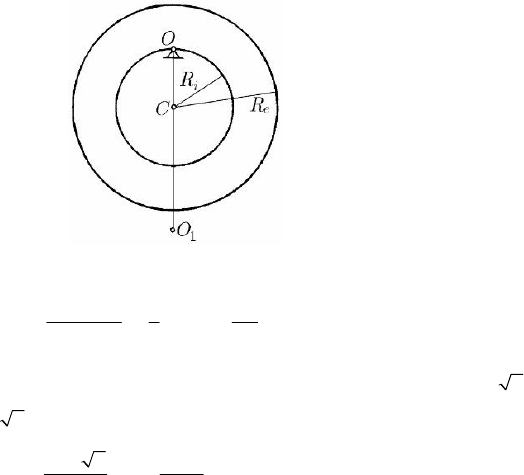
acceleration. Such a pendulum is an annular one, imagined in 1939 by L. Teodoriu and

R. Voinaroski; it is a homogeneous right cylinder of steel, having a height h and a

circular annulus section, of radii

R and

R , suspended at a centre O on the internal

face by a blade, along the respective generatrix (Fig. 14. 11). The moment of inertia

()

=−

IhRRπμ , where μ is the density; the mass of the pendulum is,

obviously, given by

()

=−

MhRRπμ , so that

()

IMRR and

()

222

iRR. We obtain thus

⎛⎞

′

=+ = +

⎜⎟

⎝⎠

lR R

(14.2.18)

Observing that

() ( )

′

=⎡− ⎤

⎣

⎦

d/d 1/2 3 /

lR RR

, we obtain

′

min

= 3

R for = /3

RR ; in this case, it results (Fig. 14.11)

43 12

gRR

ππ

(14.2.19)

The construction of the annular pendulum so that

′

have a minimal value (

′

determined in a range zone) leads to small experimental errors due to various technical

Fig. 14.11 Voinaroski’s Annular Pendulum

with respect to a central principal axis of inertia along the direction of the generatrix is

250

14.2.1.5 Voinaroski’s Annular Pendulum

MECHANICAL SYSTEMS, CLASSICAL MODELS

deficiencies. R. Voinaroski realized this pendulum in the Laboratory of Mechanics of

the University of Bucharest in the above mentioned conditions, obtaining

Buc

9.806 m/sg = (with three exact decimals).

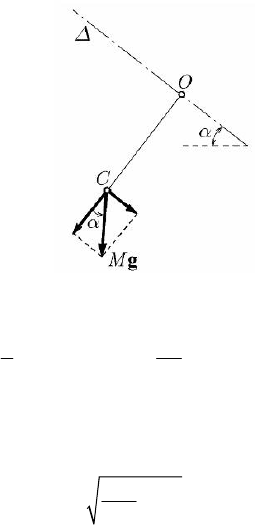
The inclined pendulum imagined by E. Mach is a physical pendulum, the suspension

axis of which is inclined by an angle

α, <<0/2απ , with respect to the horizontal

plane (Fig. 14.12). The mass centre C oscillates in a plane

Π normal to the axis

Δ, the

trace of which on the plane being just the suspension centre O. The equilibrium

position of the pendulum is that for which the moment of the own weight M

g with

respect to the

Δ-axis is equal to zero, the meridian plane determined by the axis Δ and

the centre C being vertical for this position; during the motion, the meridian plane

oscillates about this position of equilibrium. We decompose the force M

g in a

component

sinMg α , parallel to the axis Δ, and a component cosMg α , normal to

this axis, contained in the plane

Π; observing that the first component gives a null

moment with respect to the

Δ-axis, we obtain the equation of motion of Mach’s

pendulum in the form

′

sin 0

θθ



′

= cos

α .

(14.2.20)

Hence, we find again the previous results, where we replace the distance l by

cosl α . In case of isochronous oscillations, we find the period

2sec

Mgl

πα= .

(14.2.21)

Fig. 14.12 Mach’s inclined pendulum

251

14.2.1.6 The Mach Inclined Pendulum

14 Dynamics of the Rigid Solid

For

0α = we find again the period (14.2.7'), so that

cos

α = ,

(14.2.22)

and we have an experimental verification of the above obtained results.

= /2απ , then the Δ-axis is vertical and the equation of motion becomes 0θ =



;

it results a uniform rotation if

()

0tωθ=≠



. If =

0ω , then any position

()

tθθ θ== is a position of equilibrium. A door with a vertical axis illustrates this

assertion.

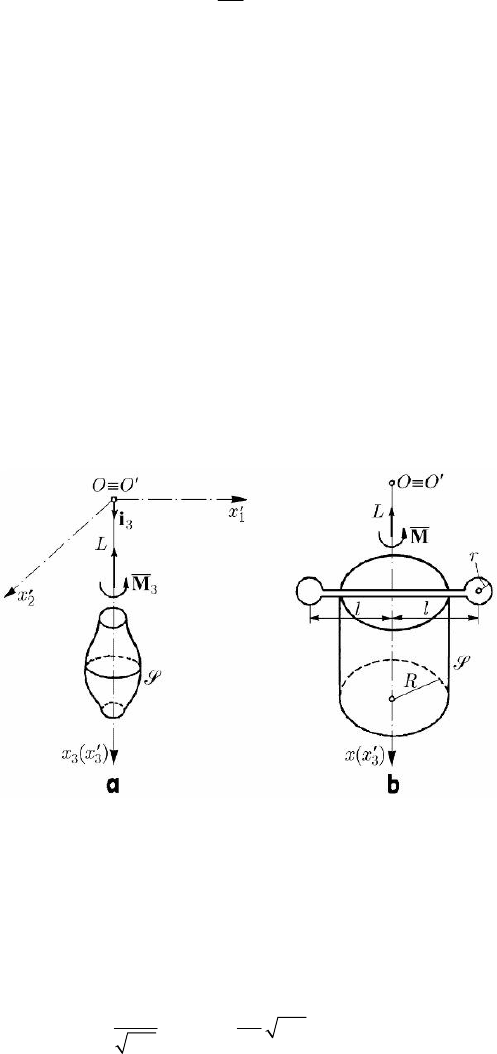
Let be a homogeneous rigid solid

S with axial symmetry, suspended at a point

′

by an inextensible thread along the symmetry axis (the descendent vertical of the point

′

), which is taken as

′′

Ox -axis (Fig.14.13,a). This solid is rotated by an angle

(till an initial position), being then let free. We obtain thus the Weber-Gauss torsion

pendulum. The thread plays the rôle of a constraint and acts as a couple of torsion of

moment

νθ=−Mi

(we take

Ox O x

′′

≡ , OO

′

≡ ) upon the rigid body, ()tθθ=

being the angle of rotation about the stable position of equilibrium. The equation of

motion with respect to the axis of rotation will be

I θνθ=−



(14.2.23)

where we assume that

kd Lνμ= , d and L being the diameter of the cross section

of the thread and its length, respectively,

is the linear density of it, while

0k >

is a

constant of the nature of an angular acceleration. We obtain thus

14.2.1.7 The Weber-Gauss Torsion Pendulum

Fig. 14.13 The Weber-Gauss torsion pendulum

252

MECHANICAL SYSTEMS, CLASSICAL MODELS

() costt

θθ

= ,

0ν >

(14.2.23')