Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

so that

TMR

ππ

νν

(14.2.24)

for isochronous oscillations.

If the rigid solid

S is a circular cylinder of radius R and mass M , then we have

/2IMR. We can verify the mathematical model considered for the torsion of

threads adding to the rigid solid two equal homogeneous spheres, each of radius r and

mass m, connected by a thin rod of length 2l and negligible mass with respect to m

(Fig. 14.13,b). Denoting by

′

I the axial moment of inertia of the new obtained

mechanical system and using the Huygens-Steiner theorem (formula (3.1.113)), we

obtain

22 4

T I ml mr

ππ

νν

′′

== ++

(14.2.24')

Assuming that the periods T and

′

are obtained experimentally, one determines the

constant

ν of torsion of the thread. Practically, the values thus obtained differ very little;

if the difference is not great, then one can assume that the determination is sufficiently

good. Eliminating

ν between the relations (14.2.24) and (14.2.24'), one obtains the

moment of inertia

by experimental determinations; this result can be of interest for

any rigid solid of revolution

The plane-parallel motion of the rigid solid is a particular case of motion which is

frequently encountered in practice. In this order of ideas, after some applications, we

make considerations concerning the dynamics of the three-dimensional motion of an

airplane and then the plane-parallel motion of it. As well, we present the motion with

sliding and rolling friction on an inclined or on a horizontal plane.

As we have seen in Chap. 5, Subsec. 2.3.4, a rigid solid

S has a plane-parallel

motion if three non-collinear points of it are contained during the motion in a fixed

plane, hence if a plane section (the

Ox x

-plane or the

Ox x

-plane) of the rigid solid

slides on a fixed plane (the

′′′

Oxx -plane); the axes

′′

and

(or

) are

normal to these planes. Without particularizing the motion, we can take the mass centre

as pole of the non-inertial frame of reference (

OC≡

) (Fig. 14.14). In this case, the

14.2.2 Plane-parallel Motion of the Rigid Solid

14.2.2.1 General results

253

14 Dynamics of the Rigid Solid

rigid solid

S has only three degrees of freedom and we can choose as parameters

which specify the motion the co-ordinates

′

and

′

(

0ρ

′

) of the mass centre C

and the angle

θ made by the axis

Cx with the axis

Cx . The fixed and the movable

axoids are two cylinders the traces of which on the fixed plane are the fixed and

movable centrods, respectively, tangent one to the other at the instantaneous centre of

rotation (see Chap. 5, Sect. 2.3.4).

Starting from the equations (14.1.48), (14.1.52), we can write the equations of

motion along the axes of the frame of reference

R in the form

()

12CC

Mv v R Rω

′′

−=+



()

Mv v R Rω

′′

+=+



0 RR=+,

(14.2.25)

31 23

II MMωω−=+



23 31

II MMωω+=+



IMMω =+



(14.2.25')

where we noticed that

′

= , while

ω= iω

; here

{

}

RM is the torsor of the

given forces, while

{

}

is the torsor of the constraint forces. Projecting the

equation (14.1.47) on the axes of the inertial frame of reference

′

R , we obtain the

scalar equations (which replace the equations (14.2.25))

MRR

′

MRR

′

0 RR=+,

(14.2.26)

where the notations correspond to these co-ordinate axes.

Fig. 14.14 Plane-parallel motion of the rigid solid

254

MECHANICAL SYSTEMS, CLASSICAL MODELS

To have a plane-parallel motion of the rigid solid, it is sufficient that three non-

collinear points of it (e.g., the points C,

()

,0,0Ph and

()

0, ,0Ph ,

,0hh> ) be

during the motion in the fixed plane; assuming that the motion of these points is

frictionless, the corresponding constraint forces are of the form

3CC

R=Ri

1133

R=Ri,

2233

R=Ri, which leads to

0RR==

31323

RR R R=++

223

MhR= ,

113

MhR=− ,

M = . Associating adequate initial conditions of

Cauchy type, we notice that the third equation (14.2.25') determines the angular

velocity

()t=ωω; then the first two equations (14.2.25) give the components

()

Cj Cj

vvt

′′

= , 1, 2j = , of the velocity of the mass centre C with respect to the inertial

frame of reference. In this case too, we can adopt correspondingly the theorem of

existence and uniqueness. The first two equations (14.2.25') allow to calculate the

components

R and

R of the constraint forces, while the third equation (14.2.25)

specifies the constraint force

R . Thus, the plane-parallel motion of the rigid solid is

statically determinate; in the case in which the number of the points of the solid which

coincide all the time with the fixed plane is greater than three, then the problem

becomes statically indeterminate (due to the model of rigid solid adopted). If the motion

of the rigid solid is a plane-parallel one, the constraint forces vanishing, one must have

0R ; hence, the resultant of the given forces must be parallel to the fixed plane. The

moment of the given forces is directed along the normal to the fixed plane

(

MM==) if and only if the

Cx -axis is a central principal axis of inertia,

hence if

23 31

0II==

. In this case, the pseudomoment of momentum

K has the

components

const

K =

const

K =

; because at the initial moment we have

KK==, it results that during the motion we have

K=Ki.

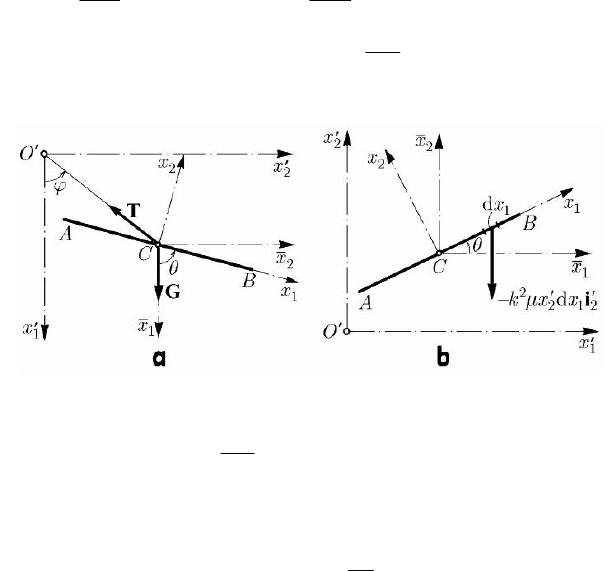
Le be a rigid straight bar AB of length 2l, which is moving in the fixed plane

′′′

Oxx (in a modelling of unidimensional solid). Assuming that the bar is

homogeneous, of linear density

μ, the mass centre will be at its middle; in the same

fixed plane, we consider also the non-inertial frames of reference

Cx x (the axes of

which are parallel to the axes of the inertial frame

′′′

Oxx ) and

Cx x

, the axis

being along the bar. The position of the bar will be specified by the co-ordinates

′

and

′

of the centre of mass and by the angle θ, made by the

Cx -axis with the

Cx -axis.

Because of the symmetry, the

-axis is a central principal axis of inertia, any normal

axis at C to that one having the same property; thus, we have

23 31

0II==. On the

other hand,

33 1 1

Ixxμ

−

∫

, so that

2/3 /3IlMlμ==, where = 2Mlμ is

the mass of the bar.

We assume that the bar is in a vertical plane and is subjected to the action of its own

weight

M=Gg; its centre of mass C is connected to the fixed point

′

by an

14.2.2.2 The Plane-Parallel Motion of a Rigid Straight Bar

255

14 Dynamics of the Rigid Solid

inextensible thread (in which arises the tension T ) (Fig. 14.15a). It results

=M0 so

that

= 0ω



, wherefrom

tθω θ=+

and

ω corresponding to the position and to

the angular velocity at the initial moment

= 0t

, respectively. The equations of motion

of the mass centre in the non-parallel frame of reference

R have the form

()

cos cos

Mv v Mg Tωθθϕ

′′

−= −−



()

sin sin

Mv v Mg Tωθθϕ

′′

+=−−−



(14.2.27)

but it is difficult to study them directly; it is more convenient to use the equations

(14.2.26), which lead to

cos

MMgT

′

=−

sin

′

=−

(14.2.27')

Observing that

coshρϕ

′

sinhρϕ

′

hOC

′

and eliminating the tension T,

we obtain the equation of the mathematical pendulum

sin 0

ϕ+=

the tension being given by

()

cos

TMg h

⎡

⎤

⎢

⎥

⎣

⎦

Hence, the centre of mass C oscillates as a simple pendulum about the fixed point

′

the bar AB rotating uniformly around it in the considered vertical plane.

Let us suppose now that the straight bar slides frictionless on a horizontal fixed plane

′′′

Oxx , being attracted by the fixed axis

′′

Ox in direct proportion to the mass and to

the distance of each point of it to this axis (Fig. 14.15b). In this case (we use the

formula (3.1.9') of static moments)

Fig. 14.15 Plane-parallel motion of a rigid straight bar

256

MECHANICAL SYSTEMS, CLASSICAL MODELS

0R =

2212

RkxxkMμρ

−

′′

=− =−

∫

constk =

the equations of motion (14.2.26) leading to

at bρ

′

()

sinAktρα

′

;

eliminating the time t, we obtain

()

sin

ρρα

⎡

⎤

′′

=−+

⎢

⎥

⎣

⎦

(14.2.28)

the trajectory of the mass centre C being a sinusoid in the fixed plane. As well (the

static moment with respect to an axis which passes through C vanishes)

()

22 2

12 1 1 2 1

MkxxxkxxxkIμμρ

−−

′′

=− =− + =−

∫∫

222

11 33

sin cos d sin cos

kxxkIμθθ θθ

−

=− =−

∫

The angle

()tθθ= verifies the equation

sin cos 0kθθθ+=



(14.2.29)

We find thus again the equation of the mathematical pendulum for the argument 2

θ; the

oscillations defined by the equation (14.2.29) have been denoted by W. Thomson and

P.G. Tait, in 1861, quadrantal oscillations. Multiplying by

2θ



and integrating, we get

222

sinkθω θ=−



(14.2.29')

where

ω is the angular velocity for = 0 ; if

kω <

, then the bar oscillates about the

axis

, while if

kω >

, then the bar has a circular motion (it rotates in the same

sense). If

= kω

, we obtain

cosωθθ=



()

ln tan

θπ

=+,

(14.2.30)

where

= 0θ for = 0t ; in this case, the bar tends to the

Cx -axis in an infinite time

(

t →∞ for /2θπ→ ).

Let be an inclined plane formed by two axes

′

and Δ

′′

, concurrent at O

′

, equally

inclined on a horizontal plane and situated over it, and let be

′′

Ox the bisectrix of the

angle formed by these axes. We put on them a rigid double cone, formed by two equal

homogeneous circular cones, the bases of which are joined, so that their common plane

coincides with the vertical plane

Π and passes through the bisectrix

′′

Ox , which makes

Sphere on an Inclined Plane

14.2.2.3 The Plane-Parallel Motion of a Rigid Double Circular Cone and of a Rigid

257

14 Dynamics of the Rigid Solid

the angle

α with the horizontal. We assume that this solid is placed, in the initial

position, at the lowest part of the angle formed by the axes

′

and Δ

′′

, in the

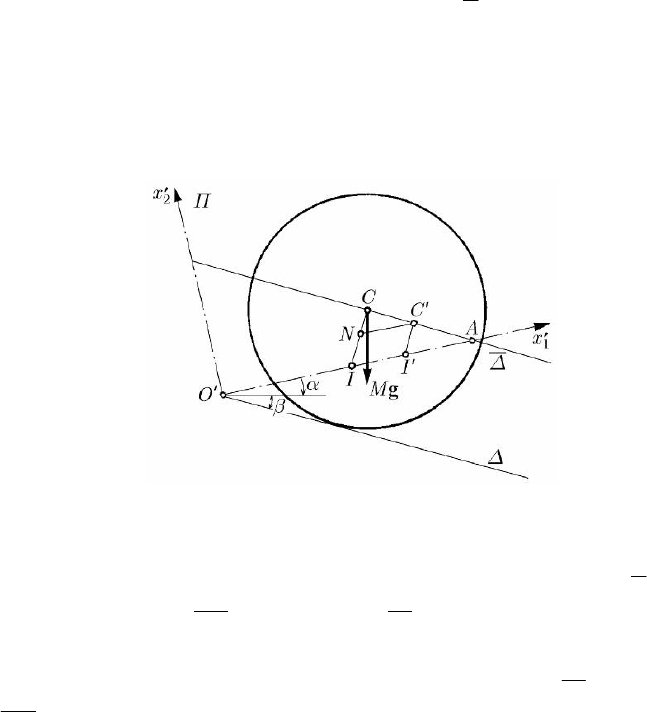
proximity of the point

′

; then, it is left to a free rolling, without sliding, on these axes,

under the action of its own weight M

g. In the fixed plane Π we specify the inertial

frame of reference

′′′

Oxx . The axes Δ

′

and Δ

′′

are projected on the plane Π along

the

′′

Ox -axis, while the points at which the double cone lays on them are projected at

the point I; as well, the vertices of the cones are projected at the point C, the centre of

mass of the double cone, the whole mechanical system being symmetric with respect to

the plane

Π. The planes which pass through the axes Δ

′

and Δ

′′

, respectively, and are

tangent to the two cones, make constant angles with the horizontal plane, being thus

fixed. Let

Δ be their intersection straight line, which is fixed too and is contained in the

plane

Π, making an angle β with the horizontal. The base circle of the two cones is

tangent to the axis

Δ, while its centre describes the axis Δ , parallel to the axis Δ. We

assume that the axis

Δ is situated below the horizontal, at the initial moment the mass

centre lying over the

′′

Ox -axis (Fig. 14.16). This plane-parallel motion, in which the

rigid solid, without initial velocity, seems to ascend on the inclined plane (its centre of

mass moves downwards), has been studied in the XIXth century by Résal, Fleury,

Mannheim and Saint-Germain.

In the plane of symmetry

Π, the point I is the instantaneous centre of rotation and

lies on the

′′

Ox -axis; hence, the straight line IC is normal to the trajectory Δ of the

point C and we have

ddCC s r θ

′

== , rIC= and d/d d d

v str trθ

′

==θ/=



where

=θω



is the angular velocity, while θ is the angle by which the double cone is

rotating, starting from an initial position. At the moment

dtt+ , =IC r becomes

Fig. 14.16 Plane-parallel motion of a rigid double cone

258

MECHANICAL SYSTEMS, CLASSICAL MODELS

dIC r r

′′

=− , ||IC IC

′′

, while the parallel through C

′

′′

Ox pierces IC at N ;

we have

()

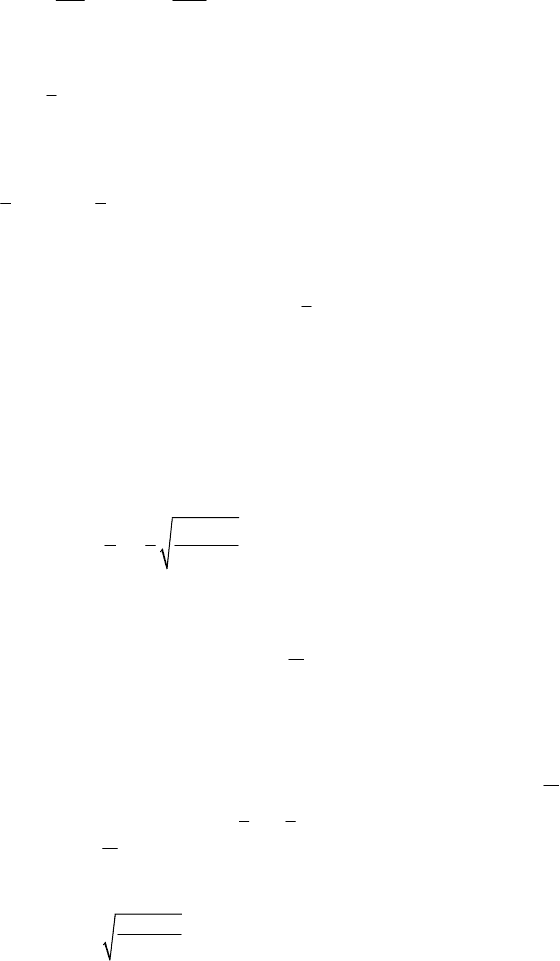
dtanCN r CC αβ

′

=− = + +

hence

()

ddcot drrρθ αβ==− + . (14.2.31)

The theorem of kinetic energy is written in the form

()

22 2 2

dsincotd

Mr Mi Mg rθθ βαβ

⎡⎤

+=− +

⎢⎥

⎣⎦



where we have used the theorem of Koenig,

i being the gyration radius with respect

to the symmetry axis of the double cone, which is a central principal axis of inertia

(

IMi= ); the elementary work is given by dM ⋅g ρ . By integration,

()

2222 2

cot

ir krrθαβ+=− +



()

2sin tankgβαβ=+,

(14.2.32)

where

r corresponds to the initial moment

0t =

, for which we have 0θ =



too.

Taking into account (14.2.31) and integrating, the time will be given by the elliptic

integral

krrr

=−

−

∫

(14.2.32')

where we have taken the sign minus because it is obvious, from a geometrical point of

view, that r diminishes starting from

r . For 0r → it results t →∞, hence the mass

centre C tends to the limit position

AOx Δ

′′

≡∩

, without reaching it (or in an

infinite time). Starting from (14.2.31) we can also write

()

tan

err

θαβ−+

()

cotss r r αβ−= − +,

(14.2.33)

where we have assumed that

0θ = for

rr= , while s is the abscissa along the

axis. Thus, the relation (14.2.32) may lead to

()tρρ= , obtaining the law of motion

of the mass centre along the

Δ -axis; the same relation shows that its velocity is given

()

cot

vkr

αβ

−

′

(14.2.32'')

259

14 Dynamics of the Rigid Solid

This velocity vanishes at the initial position

rr= and at the final position 0r = ; it

has a maximum in the interval of time in which the motion takes place. From a

kinematical point of view, the motion of the base circle of the cones is obtained rolling

the logarithmic spiral given by the first equation (14.2.33) on the

′′

-axis.

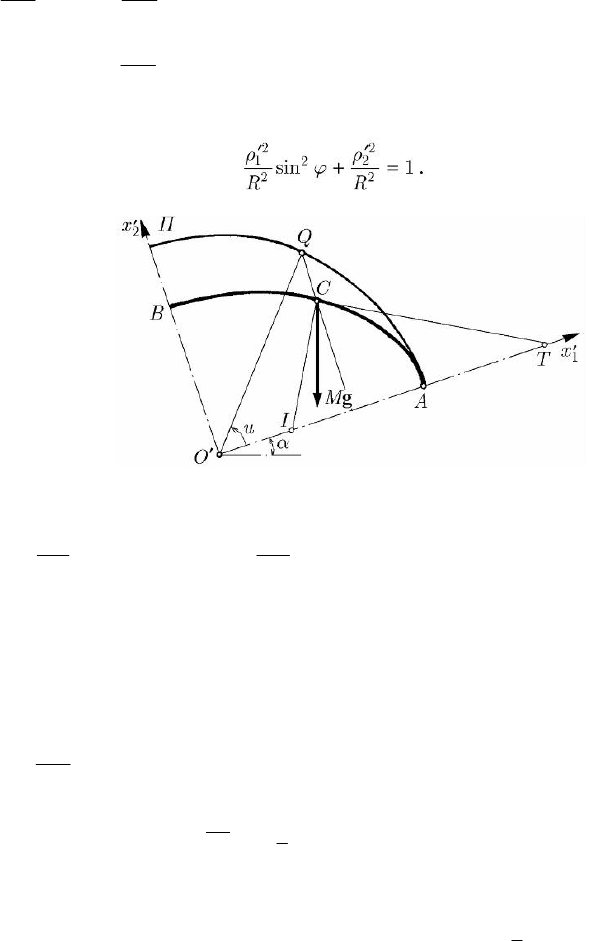
Mannheim considers in 1859 a similar problem for a homogeneous sphere of radius

R which, as well, seems to ascend on the inclined plane in the same conditions (the

centre of mass moves downwards). We keep the previous notations. If we denote by N

the point at which the axis

′

, e.g., is tangent to the sphere, we have

222

OC R ON ρρ

′′′′

=+ =+

, where we have specified the mass centre C (the

centre of the sphere) with respect to the non-inertial frame of reference

Oxx

′′′

;

observing that

cosON ρϕ

′′

, where 2ϕ is the angle formed by the axes Δ

′

and Δ

′′

it results

Hence, the centre of mass C describes an arc of ellipse of semiaxes

/sinaOAR ϕ

′

and bOB R

′

== (Fig. 14.17); the normal at C to the ellipse

pierces the

′′

-axis at the instantaneous centre of rotation I in the vertical plane Π.

The normal from C to

′′

pierces the circle of radius a and centre O

′

at Q;

introducing the eccentric anomaly u (see Chap. 9, Sect. 2.1.3, Fig. 9.8 too), the

parametric equations of the ellipse are

cosauρ

′

sinbuρ

′

. The tangent at C to

the ellipse (the equation of which is obtained by halving) pierces the

′′

-axis at T so

that

/OT a ρ

′′

; in the right triangle ICT we get

()

22222

sin cos

rIC a ub u

== + .

Fig. 14.17 Plane-parallel motion of a rigid sphere

260

MECHANICAL SYSTEMS, CLASSICAL MODELS

We can thus write

()

(

)

22222222 22

dd d sin cosd d

saubuuru

ρρ

′′

=+= + =

for the element of arc of ellipse. But

ddsrθ= , so that

()

d/dab uθ = ; the velocity of

the mass centre will be

()

vrrabuθ

′



. Applying the theorem of kinetic energy,

as in the preceding case, we get the equation

(

)

222 22

sin cos

ia ub uu

⎡⎤

⎢⎥

⎣⎦



()()

[]

2 sin cos cos cos sin singa u u b u uαα=−+−

(14.2.34)

which allows to compute the time t as function of the anomaly u by a quadrature. From

a kinematical point of view, the motion of the sphere is obtained by rolling an

epicycloid on the

′′

-axis.

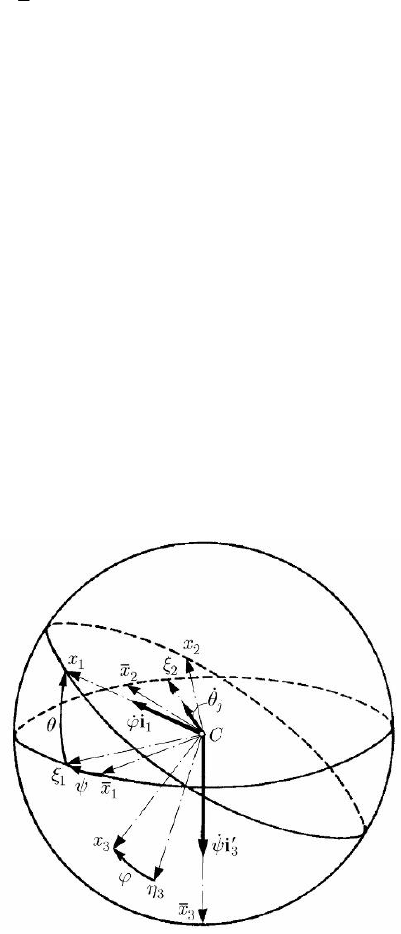
We present firstly the general equations of motion of the airplane; this one will be

modelled as a free rigid mechanical system with a plane of symmetry, subjected to the

action of given forces: own weight (dead and useful load), forces of aerodynamical

resistance and driving forces. The inertial frame of reference

′

, called geodesic

frame, has the origin

′

at the initial position of the mass centre C; the

′′

-axis is

taken along the direction of the initial velocity of the centre C and the

′′

-axis along

the descendent vertical. The non-inertial frame

R will be rigidly linked to the airplane,

having the pole at C; the

Ox -axis is along the longitudinal axis of the airplane, its

sense coinciding with the sense of advance, while the

-axis is contained in the

symmetry plane.

14.2.2.4 Dynamics of Motion of the Airplane

261

14 Dynamics of the Rigid Solid

Fig. 14.18 Dynamics of the motion of an airplane

To pass from the initial position of the airplane to its actual position, hence from the

frame

′

R to the frame R, one performs a translation, which brings the pole O

′

at the

pole C so as to coincide with the frame

R (the axes of which are parallel to those of

the frame

′

R ) and a rotation, composed of three successive rotations (Fig. 14.18); i) a

rotation of angle

ψ (angle of gyration, which puts in evidence the rotation with

respect to the initial direction), about the

Cx -axis, which carries the

Cx -axis in the

vertical plane which contains

Cx (let be

123

Cxξξ the frame in this position); ii) a

rotation of angle

θ (angle of pitching, which is the angle of inclination of the

longitudinal axis of the airplane), about the

Cξ -axis, which carries the

Cξ -axis in the

position

Cx (let

12 3

Cx ξη be the corresponding position of the frame); iii) a rotation

of angle

ϕ (the angle of rolling, which indicates the inclination on a wing), about the

axis

Cx , which carries

C ξ in the position

Cx and

C η in

Cx . These three

rotations are, in fact, specified by angles of Eulerian type (

ψ, θ and ϕ), adapted to the

problem of motion of the airplane. As in Chap. 3, Subsec. 2.2.3, we introduce the

column matrices (3.2.11), the unit vectors

i ,

1, 2, 3

, of the frame R being

expressed with respect to the unit vectors

′

i , 1,2, 3k = , of the frame

′

by means

of the matric product (3.2.11''). Noting that

cos sin 0

sin cos 0

001

ψψ

⎡⎤

⎢⎥

=−

⎢⎥

⎣⎦

cos 0 sin

01 0

sin 0 cos

θθ

⎡

⎤

−

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

10 0

0cos sin

0sincos

ϕϕ

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

−

⎢

⎥

⎣

⎦

(14.2.35)

262

MECHANICAL SYSTEMS, CLASSICAL MODELS

we introduce the matrix of components

′

=⋅ii

, ,1,2,3jk= , which specifies

the direction cosines of the axes of the frame

R with respect to the axes of the frame

R in the form

cos cos sin cos sin

sin cos cos sin sin cos cos sin sin sin cos sin

sin sin cos sin cos cos sin sin sin cos cos cos

ψθ ψθ θ

ψϕ ψθϕ ψϕ ψθϕ θϕ

⎡⎤

−

⎢⎥

=− + +

⎢⎥

+−+

⎢⎥

⎣⎦

(14.2.35')

Observing that

ψθϕ

′

=++



iω

versC ξ=





, we obtain the components of the

rotation angular velocity vector in the frame

R in the form

sinωϕψθ=−



cos sin cosωψθϕθϕ=+



cos cos sinωψθϕθϕ=−



(14.2.36)