Taylor M.E. Partial Differential Equations III: Nonlinear Equations

Подождите немного. Документ загружается.

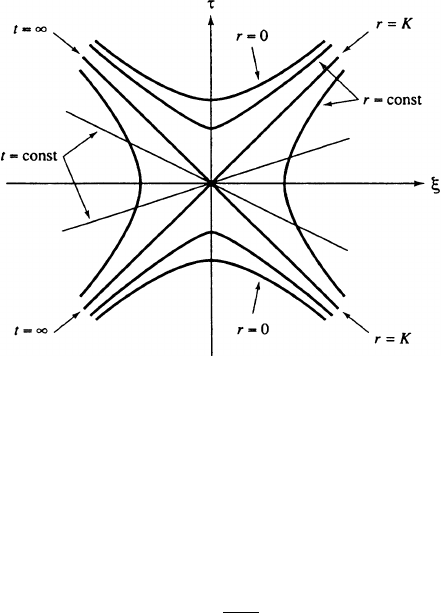
638 18. Einstein’s Equations

FIGURE 2.2 Kruskal Coordinates

where r is determined by

(2.72) 

 

D.r  K/e

r=K

;

and F is given by

(2.73) F.;/

r=K

Figure 2.2 depicts the extended Schwarzschild spacetime in Kruskal coordinates.

Exercises

1. Use Lemma 2.1 together with Theorem 1.1 to show that whenever M is a compact

manifold of dimension 2, endowed with a Riemannian metric, the integrated scalar

curvature

SdA

is independent of the choice of Riemannian metric on M . How does this ﬁt in with

proofs of the Gauss–Bonnet theorem, given in  5 of Appendix C?

2. Suppose M is a manifold with a nondegenerate metric tensor. Show that

dim M D 3; Ric

D 0 H) R

jk`

D 0:

(Hint: Show that the map (2.37) is an isomorphism when dim M D 3:)

3. Stationary and static spacetimes 639

3. Suppose in (2.4) you replace S

, with its standard metric, by hyperbolic space H

, with

Gauss curvature 1, obtaining

(2.74) ds

De



C e



C r

Show that in the formulas (2.46)–(2.48) for the Einstein tensor, the only change occurs

in (2.47), where S

D 2 is replaced by 2. Show that this has the effect precisely of

replacing e



by Ce



in the formulas (2.51)and(2.53)forG

and G

. Deduce that

a solution to the vacuum Einstein equations arises if  D and



D1 

;

for some K 2 R.TakingK>0, we have a metric of the form

(2.75) ds



1 C





1 C



1

C r

;

so r, rather than t, takes the place of “time,” and the Killing vector @=@t is not timelike.

Taking K D;  > 0, we have a metric of the form

(2.76) ds

D





 1







 1



1

C r

.r ¤ /;

and the Killing vector @=@t is timelike on fr<g.

Show that

(2.77) dr

C r

can be interpreted as the ﬂat Minkowski metric on the interior of the forward light cone

in R

. What does this mean for (2.75)?

3. Stationary and static spacetimes

Let M be a four-dimensional manifold with a Lorentz metric, of signature

.1; 1; 1; 1/.WesayM is stationary if there is a timelike Killing ﬁeld Z on M ,

generating a one-parameter group of isometries. We then have a ﬁbration M ! S,

where S is a three-dimensional manifold and the ﬁbers are the integral curves of

Z,andS inherits a natural Riemannian metric. We call S the “space” associated

to the spacetime M .

Given x 2 M ,letV

denote the subspace of T

M consisting of vectors parallel

to Z.x/,andletH

denote the orthogonal complement of V

, with respect to the

Lorentz metric on M . We then have complementary bundles V and H. Indeed,

p W M ! S has the structure of a principal G-bundle with connection, with

G D R. For each x; H

is naturally isomorphic to T

p.x/

S. The curvature of this

bundle is the V-valued 2-form ! given by

(3.1) !.X; Y / D P

ŒX; Y 

640 18. Einstein’s Equations

whenever X and Y are smooth sections of H. Here, P

is the orthogonal

projection of T

M onto V.SinceG D R, this gives rise in a natural fashion

to an ordinary 2-form on M .

We remark that the integral curves of Z are all geodesics if and only if the

length of Z is constant on M . This is a restrictive condition, which we certainly

will not assume to hold. Thus such an integral curve C can have a nonvanishing

second fundamental form II

.X; Y /,whichforX; Y 2 V

takesvaluesinH

We have the following quantitative statement:

Proposition 3.1. If Z is a Killing ﬁeld and U

is a smooth section of H,then

(3.2) hII

.Z; Z/; U

iD

hZ; Zi:

Proof. Theleftsideof(3.2) is equal to

(3.3) hr

Z; U

iDhZ; r

Z  L

Now hZ; L

iD.L

g/.Z; U

/ D 0, so the right side of (3.3) is equal to the

right side of (3.2), and the proof is complete.

Let E

and E

denote the bundles V and H, respectively, so TM DE

˚E

Let P

.x/ denote the orthogonal projection of T

M onto E

. Thus P

is as in

(3.1). If r is the Levi–Civita connection on M , we deﬁne another metric connec-

tion (with torsion)

(3.4)

rDr

˚r

;

where r

D P

on sections of E

. Thus

(3.5)

D P

C P

 C

;

where C

has the form

(3.6) C



0II



as in (4.40) of Appendix C; C is a section of Hom.TM ˝ TM;TM/.Letusset

(3.7) T

DC

The Weingarten formula states that

(3.8) C

DC

3. Stationary and static spacetimes 641

see (4.41) of Appendix C. Note that if x 2 C, an integral curve of Z,then

(3.9) X; Y 2 V

H) C

Y D II

.X; Y /:

The following is a special case of a result of B. O’Neill, [ON]. It says that A in

(3.7) measures the extent to which H is not integrable.

Proposition 3.2. If X and Y are sections of H,then

(3.10) C

Y D

ŒX; Y :

Proof. Since C is clearly a tensor, it sufﬁces to prove this when X and Y are

“basic,” namely, when they, arise from vector ﬁelds on M . Note that

ŒX; Y  D P

Y  P

X D A

Y  A

so it sufﬁces to show that A

X D 0.IfU is a section of V,then

hU; A

XiDhU; r

XiDhr

U; Xi;

where h ; i is the inner product on T

X . Now, under our hypotheses, ŒX; U  is

vertical,sohr

U; XiDhr

X; Xi, hence

hU; A

XiD

hX; XiD0;

since hX; Xi is constant on each integral curve C.

Note that C

is uniquely determined by (3.8)–(3.10), together with the fact

that it interchanges V and H.

We want to study the behavior of a geodesic on a stationary spacetime M .We

begin with the following result:

Proposition 3.3. Let  be a constant-speed geodesic on M , with velocity vector

T .IfZ is a Killing ﬁeld, then hT;Zi is constant on .

Proof. We have

(3.11)

T .s/; Z..s//

DhT;r

Zi;

if r

T D 0. Now generally the Lie derivative of the metric tensor g is given

by .L

g/.X; Y / Dhr

Z; Y iChX; r

Zi, so the right side of (3.11) is equal

to .1=2/.L

g/.T; T /.SinceZ is a Killing ﬁeld precisely when L

g D 0,the

proposition is proved.

642 18. Einstein’s Equations

Thus, if  is a geodesic on M , satisfying

(3.12) hT; T iDC

;

we have

(3.13) hT; ZiDC

There is the following relation. Set

(3.14) T D T

C T

D ˛Z C T

;

where T

is a section of V and T

a section of H. Then, by orthogonality, C

hZ; ZiChT

i, while hT; ZiD˛hZ; ZiDC

,so

(3.15) C

hZ; Zi

ChT

i;˛D

hZ; Zi

In Einstein’s theory, a constant-speed, timelike geodesic in M represents the

path of a freely falling observor. Let us consider the corresponding path in “space,”

namely, the path .s/ D p ı .s/,wherep W M ! S is the natural projection.

We want a formula for the acceleration of .

Note that if 

.s/ D T D T

D ˛Z CT

,asin(3.14), then 

.s/ D V.s/

is the vector in T

.s/

S whose horizontal lift is T

.s/. By slight abuse of notation,

we simply say V.s/ D T

.s/. Similarly,

(3.16) r

V D P

;

where P

is the orthogonal projection of T

M on H

;xD .s/. We can restate

this, using a modiﬁcation of the Levi–Civita connection r on M to

r,givenby

(3.5). Then, via the identiﬁcation used in (3.16), we have

(3.17) r

V D

DC

;

using r

T D 0.Infact,thisplus(3.5) yields

V D

 C

;

where the ﬁrst two terms on the right are sections of V and the last term is a section

of H. Thus we get (3.17), plus the identity

DC

Consequently, if U

is a vector ﬁeld on M , identiﬁed with a section of H on X ,

we have

(3.18)

V;U

iD

D

/; U



;!.T

3. Stationary and static spacetimes 643

Here, II

is the second fundamental form of the integral curve C of Z,and! is

the “bundle curvature” of M ! S,asin(3.1). The ﬁrst identity in (3.18) makes

use of (3.8), while the last identity follows from (3.9)to(3.10).

Consequently, if we deﬁne !

W H ! V by !

D !.T

/, with adjoint

W V ! H,wehave

(3.19) r

V DII

/ 

where !

/ D !

. Note that the formula (3.2)forII

can be rewritten

(3.20) II

.Z; Z/ D

grad ˆ; ˆ DhZ; Zi;

where hZ; Ziis a smooth function on M , constant on each integral curve C, hence

effectively a function on S . Thus

(3.21) II

/ D ˛

.Z; Z/ D

grad ˆ;

where C

is the constant C

DhT; Zi of Proposition 3.3.

We can rewrite !

/ as follows. Let ˇ W H ! H be the skew-adjoint

map satisfying

(3.22) !.T

/ Dhˇ.T

/; U

iZ:

We then have

(3.23) !

/ D C

ˇ.T

using the identity ˛hZ; ZiDC

from (3.15). Note that effectively ˇ is a section

of End TS, that is, a tensor ﬁeld of type (1,1) on S.

In summary, recalling the identiﬁcation of V and T

, we have the following:

Proposition 3.4. If  is a constant-speed, timelike geodesic on a stationary

spacetime M , then the curve  D p ı  on S, with velocity V.s/ D 

.s/, has

acceleration satisfying

(3.24) r

V D

grad ˆ

1



ˇ.V /:

Note a formal similarity between the “force” term containing ˇ.V / here and

the Lorentz force due to an electromagnetic ﬁeld, on a Lorentz 4-manifold. Given

initial data for .s/, namely,

(3.25) .0/ D x

2 M; 

.0/ D T.0/D T

.0/ C T

.0/;

644 18. Einstein’s Equations

we have C

DhT

.0/; Z.x

/i. The initial condition for  is

(3.26) .0/ D p.x

/; 

.0/ D T

.0/:

Conversely, once we obtain the path .s/ on S, by solving (3.24) subject to the

initial data (3.26), we can reconstruct .s/ as follows. We deﬁne T on the surface

† D p

1

./ so that

(3.27) p.x/ D .s/ H) T.x/ D ˛.s/Z C V.s/;

with ˛.s/ speciﬁed by the identity (3.15), namely,

(3.28) ˛.s/ DC



.s/



1

Then T is tangent to † and  is the integral curve of T through x

The Lorentz manifold M is said to be a static spacetime if the subbundle H is

integrable, that is, the bundle curvature ! of (3.1) vanishes. Note that if  is the

1-form on M obtained from Z by lowering indices, then

(3.29) .d/.X; Y / D XhZ; Y iY hZ; XihZ; ŒX; Y i:

If X and Y are sections of H,thisgives

(3.30) hZ; ŒX; Y iD.d /.X; Y /;

so vanishing of d on H  H is a necessary and sufﬁcient condition for inte-

grability of H. As a complement to (3.30), we remark that, since Z is a Killing

ﬁeld,

(3.31) hX; dˆiD.d /.X; Z/;

for any vector ﬁeld X on M ,where,asin(3.20), ˆ DhZ; Zi. This follows

from the identities

/.X/ D .L

g/.Z; X/; L

 D d.cZ/  .d /cZ:

If M is static, a calculation using (3.30)–(3.31) implies

(3.32) d



1





D 0:

Hence there is a function t 2 C

.M / such that

(3.33)  Dˆ dt:

3. Stationary and static spacetimes 645

It follows that the tangent space to any three-dimensional surface ft D cgDS

is given by T

D H

,forp 2 S

, and furthermore, the ﬂow F

generated

by Z (which preserves H) takes S

to S

cCt

. Each S

is naturally isometric to the

Riemannian manifold S, and the metric tensor on M has the form

(3.34) ds

Dˆ.x/ dt

C g

.dx; dx/;

where ˆ is given by (3.20)andg

is the metric tensor on S .

So, when M is static, we obtain a diffeomorphism ‰ W S  R ! M by

identifying S with S

Dft D 0g and then setting ‰.x; t/ D F

x. The geodesic

 on M yields a path on S R:

(3.35) ‰

1

..s// D



.s/;t.s/



;

where .s/ is the path in S studied above. The function t.s/ is deﬁned by (3.35).

Note that

(3.36)

D ˛.s/;

where ˛.s/ isgivenby(3.27)–(3.28). Thus we can reparameterize  by t, obtain-

ing Q.t/ such that Q.t.s// D .s/. We see that

(3.37) Q.t/ D



x.t/; t



;x.t/D .s/:

The quantities v.t/ D x

.t/ and a.t/ Dr

v.t/ are the velocity and accelera-

tion vectors of the path x.t/.Wehave

(3.38) v.t/ D x

.t/ D

˛.s/

V.s/ D

ˆ.x/V .s/:

Furthermore,

(3.39) r

v D

V 





Note that dˆ=dt Dhv; grad ˆi.Ifweuse(3.24), recalling that ˇ D 0 in this

case, we obtain the following result:

Proposition 3.5. A static spacetime M can be written as a product S  R, with

Lorentz metric of the form (3.34). A timelike geodesic on such a static spacetime

can be reparameterized to have the form (3.37), with velocity v.t/ D x

.t/, and

with acceleration given by

(3.40) r

v D

grad ˆ C

hv; grad ˆiv:

646 18. Einstein’s Equations

By (3.15)wehavehV;V iDC

C C

=ˆ, hence

(3.41) hv; viDˆ C

In particular, if .s/ is lightlike,soC

D 0,wehave

(3.42) hv; viDˆ:

This identity suggests rescaling the metric on S, that is, looking at g

D ˆ

1

We will pursue this next.

Note that the null geodesics on a Lorentz manifold M (i.e., the “light rays”),

coincide with those of any conformally equivalent metric, though they may be pa-

rameterized differently. This is particularly easy to see via identifying the geodesic

ﬂow with the Hamiltonian ﬂow on T



M , using the Lorentz metric to deﬁne the

total “energy.” If M is static, we can multiply the metric (3.34)byˆ

1

, obtaining

the new metric

(3.43) ds

Ddt

C g

.dx; dx/; g

D ˆ

1

If  is a geodesic for this new metric on M , the equation (3.40) for the projected

path x.t/ on S becomes

(3.44) r

v D 0;

as the ˆ D 1 case of (3.40). Consequently, null geodesics in a static spacetime

project to geodesics on the space S, with the rescaled metric g

D ˆ

1

Let us see what happens to geodesics that need not be lightlike. For the mo-

ment, we take M to be stationary, and deﬁne ˆ by (3.20). In order to clarify the

role of the exponent of ˆ, we consider on S a conformally rescaled metric of the

form g

D ˆ

. Farther along, we will again take a D1, and then we will

specialize to the case of M static.

The connection coefﬁcients for the two metrics g

and g

are related by

(3.45)



2ˆ



ˆ/ ı

C .@

ˆ/ ı

 g

j



ˆ/g



Equivalently, the connections r

and r

are related by

(3.46)

W Dr

W C

2ˆ



hV;grad ˆiW ChW;grad ˆiV

hV;W i grad ˆ



3. Stationary and static spacetimes 647

In particular,

(3.47) r

V Dr

V C

hV;grad ˆiV 

2ˆ

hV;V i grad ˆ:

Here, h ; i is the inner product for g

, and grad ˆ is obtained from dˆ via the

metric g

If .s/ is a geodesic (not necessarily lightlike) on a stationary spacetime M ,

then the construction of the projected path .s/ on S given by  D p ı  shows

that V D 

.s/ satisﬁes

(3.48) hV;V iDC

;

as noted after Proposition 3.5. Hence, in the lightlike case, g

.V; V / D ˆ

a1

If we want to reparameterize  to have constant speed (in the lightlike case), we

set

(3.49) Q.r/ D .s/;

D ˆ

.1a/=2

;

so g

. Q

; Q

/ D C

if .s/ is lightlike. Let

(3.50) w DQ

.r/ D ˆ

.1a/=2

V.s/:

Then (regardless of whether  is lightlike)

(3.51) r

w D ˆ

1a

V C

1  a

a

hgrad ˆ; V iV:

If we use (3.46), this becomes

(3.52)

1a



V C

hV;grad ˆiV 

2ˆ

hV;V i grad ˆ



1  a

a

hgrad ˆ; V iV:

If we use (3.48)forhV;V i and (3.24)forr

V , we see that (3.51) is equal to



1a

grad ˆ 

a





grad ˆ

1 C a

a

hV;grad ˆiV  ˆ

1a

ˇ.V /: