Taylor M.E. Partial Differential Equations III: Nonlinear Equations

Подождите немного. Документ загружается.

648 18. Einstein’s Equations

From here on, we take a D1.Wehave

(3.53) r

w D

ˆ grad ˆ 

ˆˇ.w/:

This is a generalization of (3.44). If M is static, ˇ.V / D 0,andif is lightlike,

D 0,sor

w D 0 in that case.

Note that if M is static, then w is a constant multiple of v,deﬁnedby(3.38),

and (3.53) is then equivalent to

(3.54) r

v D

ˆ grad ˆ:

In (3.54), grad ˆ is obtained from dˆ via g

.Ifweuseg

, call the vector ﬁeld

so produced grad

ˆ.Wehave

grad

f D ˆ grad f:

We have established the following:

Proposition 3.6. Let M D S  R be a static spacetime, with metric of the form

(3.34). Let  be a timelike geodesic on M , reparameterized to have the form

(3.37), yielding a curve x.t/ on S, with velocity v.t/ D x

.t/. With respect to the

rescaled metric g

D ˆ

1

on S, this curve satisﬁes the equation

(3.55) r

v D

grad

ˆ:

Recall that C

and C

are given by (3.12)–(3.13). We mention that, while the fac-

tor C

is constant on each orbit, it varies from orbit to orbit. For example, if

at time t

a particle moving along  is “at rest,” so 

/ is parallel to Z,where

t.s

/ D t

,thenC

Dˆ.x

1

,wherex

D x.t

/, as follows from (3.15).

Exercises

Exercises 1–5 deal with the Kerr metric, which, in .t;r;;'/-coordinates, is

(3.56) ds

D





dta sin

'd





C

sin





/da dt



;

where

A D r

 Kr C a

;

D r

C a

cos

Here, K>0and a are constants. Note that the case a D 0 gives the Schwarzschild

metric (2.61).

1. Show that the Kerr metric provides a solution to the vacuum Einstein equation

D 0:

4. Orbits in Schwarzschild spacetime 649

2. Show that @=@t is a Killing ﬁeld and hence that the Kerr metric is stationary.

3. Show that the Kerr metric is not static (if a ¤ 0). Compute the 2-form ! of (3.1).

4. Contrast the metric induced by (3.56) on surfaces t D const. with the three-dimensional

Riemannian metric constructed at the beginning of this section.

5. Try to provide a “simple” derivation of the metric (3.56).

4. Orbits in Schwarzschild spacetime

We want to describe timelike geodesics in the Schwarzschild metric, which (for

r>K) is a static, Ricci-ﬂat metric of the form

(4.1) ds

Dˆ.r/ dt

C ˆ

1

.r/ dr

C r

;ˆ.r/D 1 

;

where d!

is the standard metric on the unit sphere S

.Thisisoftheform(3.34),

with ˆ depending only on r,andg

.dx; dx/ D ˆ.r/

1

. Thus, by

Proposition 3.6, a timelike geodesic (reparameterized) within the region r>K

has the form Q.t/ D



x.t/; t



,wherev.t/ D x

.t/ satisﬁes the equation (3.55),

namely,

(4.2) r

v D grad

ˆ;  D

This involves the rescaled metric g

D ˆ

1

, which has the form

(4.3) g

.dx; dx/ D ˆ.r/

2

C ˆ.r/

1

Symmetry implies that x.t/ is conﬁned to a plane, so we can restrict attention

to the associated planar problem, with

(4.4)

.dx; dx/ D ˆ.r/

2

C ˆ.r/

1

d

D ˛.r/

1

C ˇ.r/

1

d

We use the method discussed in  17 of Chap. 1 to treat this problem. We have a

Hamiltonian system of the form

(4.5) Py

@

; P

D

; P

D 0;

with

(4.6) F.y

;

/ D

˛.y

/

ˇ.y

/

C ˆ.y

650 18. Einstein’s Equations

where y

D r; y

D . The ﬁrst set of equations in (4.5) yields

(4.7) Pr D ˆ.r/



;

 D L

ˆ.r/

;

where L is the constant value of 

along the integral curve of (4.5). Now

F.y

;

;L/ D E is constant along any such integral curve. Solving for 

and

substituting into the ﬁrst equation in (4.7), we have

(4.8) Pr D˙ˆ.r/



2E  2ˆ.r/  L

ˆ.r/



1=2

We can rewrite this as

(4.9) Pr D˙ˆ.r/



E C

2K





1=2

;

E D E :

Compare this with (17.16) of Chap. 1:

(4.10) Pr D˙



2E C





1=2

;

for the Kepler problem, with potential v.r/ DK=r.WehaveashiftinE,a

correspondence K 7! K, and an extra term KL

, within large parentheses

in (4.9).

Next, setting u D 1=r,wehave

(4.11)

Dr

d

;

parallel to (17.21) of Chap. 1, and using

 D Lˆ.r/=r

we have

(4.12)

DLˆ.r/

d

hence, via (4.9),

(4.13)

d

D



E C 2Ku L

C KL



1=2

Compare the Kepler problem, where dr=dt DLd u=d, and hence, from (4.10),

(4.14)

d

D



2E C 2Ku L



1=2

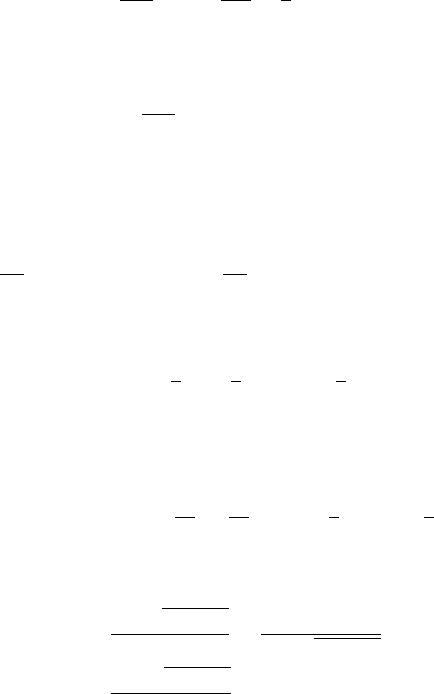
4. Orbits in Schwarzschild spacetime 651

It is useful also to consider a second-order ODE for u D u./. Squaring (4.13)

and taking the -derivative, we obtain (either u

./ D 0 or)

(4.15)

d

C u D

K

Following [ABS], p. 207, we write this as

(4.16)

d

C u D A C "u

The " D 0 case arises from the study of the Kepler problem; cf. (17.24) of Chap. 1.

A phase-plane analysis of (4.16) is useful. If v D du=d,wehavethe

“Hamiltonian system”

(4.17)

d u

d

D v D @

F.u;v/;

d

D A  u C "u

D@

F.u;v/;

where

(4.18) F.u;v/ D

 Au 

Of course, orbits for (4.18) lie on level curves F.u;v/D E

, bringing us back to

(4.13). See Figs. 4.1–4.4. In these four ﬁgures we have, respectively

" D 0; 0 < A" <

;

<A"<

;A"D

Also, in Figs. 4.2–4.3,wehave

˛ D

1 

1  4A"

1 C

1  4A"

;

ˇ D

1 C

1  4A"

We perceive the periodicity of u as a function of , on those level curves dif-

feomorphic to the circle. The period is not 2, generally, if " ¤ 0,sowehave

precession of the perihelion.

Not all the closed orbits for (4.33) depicted in Figs. 4.2–4.4 correspond to

bound orbits for the solution x.t/ to (4.2). One mechanism behind this arises

already in the " D 0 case. Take a level curve in Fig. 4.1 which crosses the vertical

axis fu D 0g.Nowu D 0 means r D1,soasu ! 0 along such an orbit, x.t/

tends to inﬁnity; this endures for an inﬁnite span of time. Such situations also arise

for positive values of ".

652 18. Einstein’s Equations

FIGURE 4.1 Orbits for (4.16), " D 0

FIGURE 4.2 Orbits for (4.16), 0<A"<

FIGURE 4.3 Orbits for (4.16),

< A"<

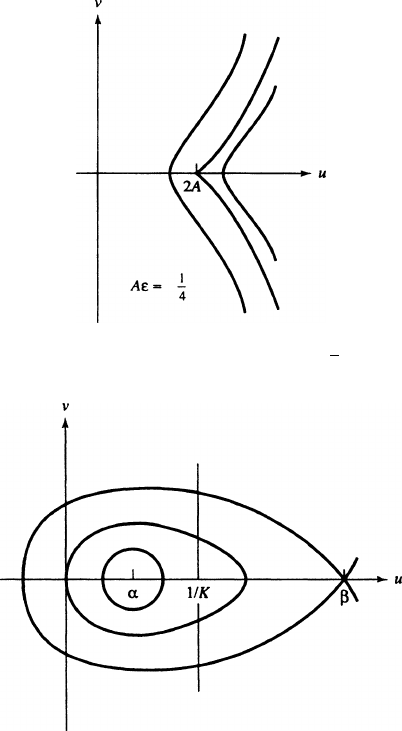
4. Orbits in Schwarzschild spacetime 653

FIGURE 4.4 Orbits for (4.16), A" =

FIGURE 4.5 Crossing the Threshold

In addition, in the case under consideration in this section, there is another

mechanism at work. Namely, consider a level curve that crosses the vertical line

fu D 1=Kg,asinFig.4.5.From(4.9) we see that as u % 1=K (so r & K),

t %1. Now, in this case, it does not take the body “forever” to cross the thresh-

old. When one switches to Eddington–Finkelstein coordinates (or to Kruskal

coordinates), one can see the planet entering the zone r<Kin ﬁnite “proper

time.” The analysis of the geodesic within this region is not radically different

from that done above, though there are some differences, since in this region the

Killing ﬁeld @=@t is not timelike. We leave it to the reader to work out the nature

of the orbit in this region, but note that indeed, a body crossing the threshold will

not be able to exit.

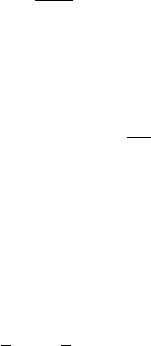
654 18. Einstein’s Equations

Let us look at the problem of determining the period p."/ of a solution w D

w."; / to an ODE of the form

(4.19)

d

C w D " .w/:

This is related to (4.16)byw D u  A; .w/ D .w C A/

. To specify uniquely

a solution, let us take

(4.20) w."; 0/ D a;

d

w."; 0/ D 0:

If v D dw=d (and we denote this by Pw), then we have the system

(4.21) Pw D v; Pv Dw C " .w/;

as in (4.17), and orbits lie on level curves of the function F

,givenby

(4.22) F

.w; v/ D

 "‰.w/; ‰.w/ D

.w/ dw:

It is clear that, for " small, we have smooth, real-valued functions ."; / and

'."; /, uniquely speciﬁed by

(4.23) w C iv D ."; /e

i'.";/

By (4.20), we have

(4.24) ."; 0/ D a; '."; 0/ D 0:

Note also that

(4.25) .0; / D a; '.0; / D :

Then p."/ is a smooth function of ", satisfying

(4.26) p.0/ D 2; '



"; p."/



D 2:

We can derive a system of ODE for ; ', as functions of . The system (4.21)

implies

Pw C i Pv D v  iw C i" .w/ Di.w C iv/ C i" .w/:

Writing the left side as .d=d/.e

i'

/ D . P  i P'/e

i'

and the right side as

ie

i'

C i" .cos '/, we obtain

4. Orbits in Schwarzschild spacetime 655

(4.27)

P D" . cos '/ sin ';

P' D 1  "

1

. cos '/cos ':

A particularly signiﬁcant quantity we can compute is p

.0/.By(4.26), we have

.0/

@

.0; 2/ C

.0; 2/ D 0;

(4.28) p

.0/ D

.0; 2/:

To compute the right side of (4.28), write

(4.29)  D a C "

./ C;'D  C "'

./ C:

Substituting into (4.27), we obtain

(4.30) P

D .a cos /sin ; P'

D

.a cos /cos :

Also, from (4.24)wehave'

.0/ D 0,so

(4.31) p

.0/ D'

.2/ D

2

.a cos /cos d:

In the case .w/ D .w C A/

, we can evaluate the integral, to get

(4.32) p

.0/ D 2A:

The integral that arises in (4.31) is often interpreted as an average, and the calcu-

lation above is sometimes said to involve the “method of averaging.” For more on

this topic, one can see [SV].

The accuracy achieved when these formulas were applied to the calculation of

the precession of the perihelion of the planet Mercury–or rather that part of it not

attributable to perturbations produced by the other planets–provided early positive

evidence in favor of Einstein’s theory of gravity.

We end this section with a remark on the value of K in (4.1), in terms of

Newtonian concepts. Newtonian theory should be accurate for a planetary orbit

on which r is large and the velocity of the planet is small. Let us evaluate the

quantity ,deﬁnedin(4.2). We have

(4.33)  D

D

hT; Ti

hT; Zi

;

656 18. Einstein’s Equations

by (3.12)–(3.13). Now, “small velocity” means T is essentially parallel to Z;

hence hT; T ihT;Zi

,andso

(4.34)  

If also r is large, then (4.9) becomes

(4.35)

Pr ˙



1 



1



E C





1=2

˙

E C .1  4



 2

C 2K

1=2

For the Newtonian approximation to be valid, we need

E<<1.AlsoA" << 1,

with A" D 3K

=.2L

/;inotherwords,K

<< L

. Thus,

(4.36) Pr ˙



E C





1=2

If we compare this with the formula (4.10) arising from the Kepler problem, we

see one difference; (4.10)has2K instead of K. Since, in appropriate units, the K

in (4.10) is the gravitational mass of the attracting body (e.g., the Sun), we con-

clude that in (4.36), K should be twice the gravitational mass. Thus, it is common

to write the Schwarzschild metric as

(4.37) ds

D



1 





1 



1

C r

and identify M as the “mass” of the solution, as seen at inﬁnity.

Exercises

1. In Fig.4.3, consider the orbit with .ˇ; 0/ as forward and backward limit points. Assume

ˇ < 1=K. Interpret the behavior of the corresponding solution x.t/ of (4.2).

2. Study timelike geodesics for the metric (4.1)insidefr<Kg.

3. Study the behavior of timelike geodesics on a spacetime with a Kerr metric, given by

(3.56). One might consult the treatment in [Chan2].

5. Coupled Maxwell–Einstein equations

The coupled Maxwell–Einstein equations are

(5.1) G

D 8T

;dF D 0; d

F D 0;

5. Coupled Maxwell–Einstein equations 657

in a spacetime in which there is an electromagnetic ﬁeld F, but no matter. The last

two equations in (5.1) are the Maxwell equations, discussed in  11 of Chap. 2.

The stress-energy tensor of F is given by (1.4), that is,

(5.2) T

4





We look for spherically symmetric solutions to (5.1). Thus, as in  2,weﬁrst

take the metric to have the form (2.4), so that G

is given by (2.51)–(2.55). The

hypothesis that F is spherically symmetric restricts its form severely. In fact, we

can write

F D d A C c.t; r/;

where A is a 1-form and  is the standard area form on S

. The equation d F D 0

implies c.t; r/ D c, constant. If we assume the electromagnetic ﬁeld decays to

zero as r !1,thenc D 0. We will make this hypothesis. By averaging with

respect to the SO.3/ action, we can arrange that A be invariant under this ac-

tion. This implies that, for each orbit O of SO.3/, the pull-back j



A 2 ƒ

.O/

vanishes. Indeed, ƒ

.O/ has no SO.3/-invariant elements other than zero; equiva-

lently, the sphere S

has no SO.3/-invariant vector ﬁelds, other than zero. Hence,

A has the form

(5.3) A D a.t; r/ dt Cb.t;r/ dr;

(5.4) F D





dt ^dr D E.t; r/ dt ^ dr:

Thus, the only nonzero components of F

are F

DF

We deduce that all off-diagonal components of T

vanish and that

(5.5)

4T



;4T

D



;

4T

.C/

if j D 2; 3:

In particular, since T

D 0, it follows that G

D 0,so(2.52) implies @=@t D 0,

that is,  D .r/. If we exploit G

D 8T

and G

D 8T

,using(2.51)

and (2.53), we get

(5.6) E.t; r/

D



1  r

 e



D



1 C r

 e

