Taylor M.E. Partial Differential Equations III: Nonlinear Equations
Подождите немного. Документ загружается.


628 18. Einstein’s Equations
where
(2.10)
B
`
jk
D
1
2
g
`
g
S
j
@
k
Cg
S
k
@
j
g
S
jk
@
D
1
2
`
j
@
k
# C
`
k
@
j
# g
S
jk
@
`
:
Here we have set
(2.11) # D log ;
and, in a product coordinate system such as described above,
`
j
D 1 if j D ` is
an index for S; 0 otherwise. We can write
(2.12)
`
j
D e.`/ı
`
j
;
where e.`/ D 1 if ` L; e.`/ D 0 if `<L. Note that
`
j
produces a well-
defined tensor field of type .1; 1/ on M D U S, namely T
x
M T
x
0
U ˚T
x
00
S,
and .x/ is the projection of T
x
M onto T
x
00
S, annihilating T
x
0
U .
Now, given p D .p
0
;p
00
/ 2 M D U S, let us use product-exponential co-
ordinates centered at p, namely, the product of an exponential coordinate system
on U centered at p
0
and an exponential coordinate system on S centered at p
00
.
In such a coordinate system, we have
(2.13) R
j
k`m
D
U
R
j
k`m
C
S
R
j
k`m
C D
j
k`m
;
with
(2.14) D
j
k`m
D @
`
B
j
km
@
m
B
j
k`
C B
j
`
B
km
B
j
m
B
k`
; at p:
The formula (2.10)forB
`
jk
is valid in any coordinate system. In product-
exponential coordinates we have
(2.15) @
`
B
j
km
D
1
2
j
k
@
`
@
m
# C
j
m
@
`
@
k
# g
S
km
@
`
@
j
;
at p.Also,
@
m
B
j
k`
D
1
2
j
k
@
m
@
`
# C
j
`
@
m
@
k
# g
S
k`
@
m
@
j
;
at p,so
(2.16)
@
`
B
j
km
@
m
B
j
k`
D
1
2
j
m
@
`
@
k
#
j
`
@
m
@
k
# g
S
km
@
`
@
j
C g
S
k`
@
m
@
j
;
2. Spherically symmetric spacetimes and the Schwarzschild solution 629
at p.From(2.10)wehave
(2.17)
4B
j
`
B
km
D
j
k
@
`
#@
m
# C
j
m
@
`
#@
k
#
g
S
k`
@
j
@
m
# g
S
`m
@
j
@
k
#
j
`
hd#;d ig
S
km
;
where
(2.18) hd#;d iD@
#@
:
Antisymmetrizing (2.17) with respect to ` and m,wehave
(2.19)
4
B
j
`
B
km
B
j
m
B
k`
D
j
m
@
`
#
j
`
@
m
#
@
k
#
C
g
S
km
@
`
# g
S
k`
@
m
#
@
j
C
j
m
g
S
k`
j
`
g
S
km
hd#;d i:
We can produce a formula for D
j
k`m
where each term is manifestly a tensor.
To get this, first note that the tensor whose components in a product-exponential
coordinate system are @
`
@
k
# is #
I`Ik
.1=2/hd ;d#ig
S
`k
. In fact, in any product
coordinate system,
(2.20)
#
I`Ik
D @
`
@
k
#
`k
@
#
D @
`
@
k
#
U
`k
@
# B
`k
@
#
D @
`
@
k
# C
1
2
hd ;d#ig
S
`k
U
`k
@
#:
The last identity follows from (2.10) plus the fact that we are summing only over
<L. Then, from (2.16)and(2.19) we obtain
(2.21)
D
j
k`m
D
1
2
h
j
m
#
IkI`
j
`
#
IkIm
g
S
km
Ij
I`
C g
S
k`
Ij
Im
i
C
1
4
h
j
m
#
Ik
#
I`
j
`
#
Ik
#
Im
C g
S
km
Ij
#
I`
g
S
k`
Ij
#
Im
i
;
in any product coordinate system.
Contracting (2.13), we have
(2.22) Ric
km
D Ric
U
km
C Ric
S
km
C F
km
;F
km
D D
j
kj m
:
Thus, in product-exponential coordinates centered at p 2 M ,wehave
(2.23) F
km
D @
j
B
j
km
@
m
B
j
kj
C B
j
j
B
km
B
j
m
B
kj
;
at p. We evaluate this more explicitly, using (2.16)and(2.19).
630 18. Einstein’s Equations
Contracting (2.16) over j D `,wehave
(2.24)
@
j
B
j
km
@
m
B
j
kj
D
1
2
j
m
@
j
@
k
#
j
j
@
m
@
k
# g
S
km
@
j
@
j
C g
S
kj
@
m
@
j
D
1
2
M@
m
@
k
#
1
2
g
S
km
L ;
at p,whereM D dim S and L D @
j
@
j
.Since 2 C
1
.U /,wehave
(2.25) L D
X
j L1
@
j
@
j
D g
km
U
@
k
@
m
D
U
;
at p. Note that
U
is the Laplace operator on U . (For our case of primary interest,
U has a Lorentz metric, so we use
U
rather than
U
:) Contracting (2.19) over
j D `,wehave
(2.26)
B
j
j
B
km
B
j
m
B
kj
D
1
4
M.@
m
#/.@
k
#/
1
4
.M 2/hd#;d ig
S
km
:
Thus we obtain, at p,
(2.27)
F
km
D
1
2
M@
m
@
k
#
1
2
.
U
/g
S
km
1
4
M.@
m
#/.@
k
#/
1
4
.M 2/hd#;d ig
S
km
:
To write this in tensor form, we recall the computation (2.20). Hence, in any
product coordinate system,
(2.28) F
km
D
1
2
M
#
IkIm
C
1
2
#
Ik
#
Im
1
2
U
hd#;d i
g
S
km
:
The scalar curvature of M is S D g
km
Ric
km
.By(2.22), we have
(2.29) S D S
U
C
1
S
S
C ˇ; ˇ D g
km
F
km
:
The formula (2.27) yields
(2.30)
ˇ D
1
2
Mg
km
U
@
m
@
k
#
1
2
M
1
U
1
4
Mg
km
U
.@
m
#/.@
k
#/
1
4
.M 2/M
1
hd#;d i;

2. Spherically symmetric spacetimes and the Schwarzschild solution 631
at p. Note that
(2.31) g
km
U
@
m
@
k
# D g
km
U
@
m
1
@
k
D
1
U
2
g
km
U
.@
m
/.@
k
/;
at p. Hence
(2.32) ˇ DM
1
U
1
4
.M
2
3M /
2
hd ;d i:
As a check on this calculation, consider the simple case dim U D dim S D 1,
with
(2.33) g
U
D dx
2
0
;g
S
D dx
2
1
;gD dx
2
0
C .x
0
/dx
2
1
:
Of course, S
U
D S
S
D 0 here, and (2.29)and(2.32) yield for the scalar curvature
of M ,
(2.34) S D
1
.x
0
/
00
.x
0
/ C
1
2
2
.x
0
/
0
.x
0
/
2
:
Since S D 2K; K being the Gauss curvature of the two-dimensional surface M ,
this formula agrees with the E D 1; G D case of formula (3.37) in Appendix
C, for the Gauss curvature of a surface with metric Edu
2
C Gdv
2
.
We now look at the Einstein tensor of M; G
jk
D Ric
jk
.1=2/Sg
jk
.Inview
of (2.22)and(2.29), we have
(2.35)
G
jk
D Ric
U
jk
C Ric
S
jk
C F
jk
1
2
S
U
.g
U
jk
C g
S
jk
/
1
2
1
S
S
.g
U
jk
C g
S
jk
/
1
2
ˇg
jk
:
Rearranging terms, we can write
(2.36) G
jk
D G
U
jk
C G
S
jk
1
2
.S
U
g
S
jk
C S
S
1
g
U
jk
/ C F
jk
1
2
ˇg
jk
:
Before considering the case dim S D 2, let us first consider the case dim U D
dim S D 1.ThenU and S are flat, and (2.36) becomes G
jk
D F
jk
.1=2/ˇg
jk
.
Let us parameterize U and S by arc length. The case M D 1 of (2.27)is
F
jk
D
1
2
@
j
@
k
#
1
2
.
U
/g
S
jk
1
4
.@
j
#/.@
k
#/ C
1
4
1
hd ;d ig
S
jk
:
Here,
U
D
00
.x
0
/; @
j
@
k
# D #
00
.x
0
/ for j D k D 0; 0 otherwise, and
@
j
# D #
0
for j D 0; 0 otherwise. Also, in this case (2.32)(or(2.34)) implies
ˇ D
1
00
C.1=2/
2
.
0
/
2
. It readily follows that F
jk
D .1=2/ˇg
jk
, hence
G
jk
D 0. This is part of a more general result.
632 18. Einstein’s Equations
Lemma 2.1. If M is a two-dimensional manifold with a nondegenerate metric
tensor, then its Einstein tensor always vanishes, G
jk
D 0.
Proof. Generally, Ric
k
m
is produced from R
jk
`m
via a natural map
(2.37) W End.ƒ
2
T
p
M/ ! End.T
p
M/:
Since ı
jk
jm
D .n 1/ı
k
m
, we see that .I/ D .n 1/I,whenn D dim M .
Now, if dim M D 2,thenƒ
2
T
p
M is one-dimensional. Hence Ric
k
m
must be a
scalar multiple of ı
k
m
,soRic
km
must be a scalar multiple of g
km
. Comparing
traces, we see that the multiple must be S=2,so
Ric
jk
D
1
2
Sg
jk
when dim M D 2:
This precisely says that G
jk
D 0. Compare the derivation of (3.35)in
Appendix C.
Let us now consider the case dim S D 2.From(2.28), we have
(2.38) F
jk
D#
Ij Ik
1
2
.
U
/g
S
jk
C
1
2
hd ;d#ig
S
jk
1
2
#
Ij
#
Ik
in any product coordinate system. Contracting this, or alternatively taking the
M D 2 case of (2.32), we have
(2.39) ˇ D2
1
U
C
1
2
2
hd ;d i:
When dim S D 2, we have from Lemma 2.1 that G
S
jk
D 0.
If also dim U D 2,thenG
U
jk
D 0,so(2.36) yields
(2.40) G
jk
D
1
2
S
U
g
S
jk
C S
S
1
g
U
jk
C F
jk
1
2
ˇg
jk
;
with F
jk
and ˇ given by (2.38)and(2.39).
Now, whenever a two-dimensional surface U has a metric tensor of the form
(2.41)
0
dx
2
0
C
1
dx
2
1
;
with
j
D
j
.x
0
;x
1
/, we readily obtain from (2.8) the formulas for the connec-
tion coefficients:
U
0
jk
D
1
2
0
@
0
0
@
1
0
@
1
0
@
0
1
;
U
1
jk
D
1
2
1
@
1
0
@
0
1
@
0
1
@
1
1
:

2. Spherically symmetric spacetimes and the Schwarzschild solution 633
In the case (2.4), we have
(2.42)
0
De
;
1
D e
;
where and are functions of .u
0
; u
1
/. This yields
(2.43)
U
0
jk
D
1
2
@
0
@
1
@
1
e
@
0
;
U
1
jk
D
1
2
e
@
1
@
0
@
0
@
1
:
Also, in the case (2.4), D .r/ D r
2
,wherer D x
1
,and# D 2 log r.
Consequently, by (2.20),
(2.44) #
Ij Ik
D @
j
@
k
# C
1
2
1
hd ;d ig
S
jk
w
jk
;
where @
1
@
1
# D2=r
2
;@
j
@
k
# D 0 for other indices, and
(2.45)
w
jk
D
1
r
e
@
1
@
0
@
0
@
1
;
for 0 j; k 1; w
jk
D 0 for other indices.
Hence for the metric tensor (2.4), the 4 4 matrix .G
jk
/ splits into two 2 2
blocks:
(2.46) G
jk
D
e
G
jk
C
b
G
jk
:
The upper left block is
(2.47)
e
G
jk
D
1
2
S
S
1
g
U
jk
1
2
ˇg
U
jk
@
j
@
k
# C w
jk
1
2
.@
j
#/.@
k
#/
D
1
2
1
S
S
2
U
C
1
2
1
hd ;d i
g
U
jk
w
jk
;
since, for # D 2 log r,wehave@
j
@
k
# C .1=2/.@
j
#/.@
k
#/ D 0. The lower right
block is
(2.48)
b
G
jk
D
1
2
S
U
g
S
jk
1
2
ˇ g
S
jk
1
2
.
U
/g
S
jk
D
1
2
S
U
U
C
1
2
1
hd ;d i
g
S
jk
:
634 18. Einstein’s Equations
Thus, for metrics of the form (2.4), G
jk
has 6 nonzero components, out of 16
(or, if symmetry is taken into account in counting components, it has 5 nonzero
components, out of 10).
When the metric tensor of U has the form e
dt
2
C e
dr
2
, the calculation
of Gauss curvature in (3.37) of Appendix C gives
(2.49)
S
U
D e
.C/=2
@
r
.
r
e
./=2
/ C @
t
.
t
e
./=2
/
De
rr
C e
tt
1
2
r
.
r
r
/e
C
1
2
t
.
t
t
/e
:
Here,
r
D @;
t
D @=@t, and so forth. Of course, the unit sphere S
2
has
Gauss curvature 1,soS
S
D 2. Also, we have, for .r/ D r
2
,
(2.50)
U
D 2e
C r.
r
r
/e
;
1
hd ;d iD4e
:
The formulas (2.45), (2.49), and (2.50) specify all the ingredients in (2.47)and
(2.48).
We conclude that, for a metric of the form (2.4), with .x
0
;x
1
;x
2
;x
3
/ D
.t;r;';/, all the nontrivial components of G are specified by the following five
formulas:
G
00
D
e
r
2
1 r
r
e
;(2.51)
G
01
D G
10
D
t
r
;(2.52)
G
11
D
1
r
2
1 C r
r
e
;(2.53)
G
22
D
1
2
r
2
e
rr
C
1
2
2
r
C
1
r
.
r
r
/
1
2
r
r
(2.54)
1
2
r
2
e
tt
C
1
2
2
t
1
2
t
t
;
G
33
D sin
2
'G
22
:(2.55)
Having determined the Einstein tensor for a spherically symmetric spacetime
that has been put in the form (2.4), we now examine when the empty-space Ein-
stein equation is satisfied, namely, when G
jk
D 0. If we require all components
G
jk
to vanish, then (2.52) implies @=@t D 0,or D .r/.Furthermore,(2.51)
and (2.53)imply
(2.56) @
r
. C / D 0;
or .r/ C .r; t/ D f.t/. Now, replacing t by t
0
D '.t/ has the effect of adding
an arbitrary function of t to in (2.4), so we can arrange that C D 0. Thus
themetric(2.4) takes the form
2. Spherically symmetric spacetimes and the Schwarzschild solution 635
(2.57) ds
2
De
.r/
dt
2
C e
.r/
dr
2
C r
2
d!
2
:
Note that the coefficients are independent of t! We say the metric is static.The
observation that a spherically symmetric solution to G D 0 must be static (un-
der the additional hypotheses made at the beginning of this section) is known as
Birkhoff’s theorem.
For the metric (2.57), the component G
01
,givenby(2.52), certainly vanishes,
and G
00
D 0 D G
11
if and only if
(2.58) r
0
.r/ D e
.r/
1:
If we set .r/ D e
.r/
, this ODE becomes r
0
.r/ D 1 .r/, a nonhomoge-
neous Euler equation with general solution .r/ D 1 K=r. Hence
(2.59) e
.r/
D 1
K
r
:
It remains to check that G
22
vanishes for this metric, that is, that
(2.60)
00
.r/ C
0
.r/
2
C
2
r
0
.r/ D 0:
This is straightforward to check. Rather than substituting .r/,givenby(2.59),
into (2.60), we can differentiate (2.58)togetr
00
C
0
D
0
e
; adding r.
0
/
2
C
0
to both sides and again using (2.58), we obtain (2.60).
We have derived the following metric, known as the Schwarzschild metric,
satisfying the vacuum Einstein equation G D 0:
(2.61) ds
2
D
1
K
r
dt
2
C
1
K
r
1
dr
2
C r
2
d!
2
:
We can readily check that this is not a flat metric in a funny coordinate system,
unless K D 0. Indeed, by (2.13)wehaveR
0
101
D
U
R
0
101
,sinceD
0
101
D 0 by
(2.21). Now
U
R
0
101
is a nonzero multiple of S
U
, and, by (2.49), we have
S
U
D
2K
r
3
;
in this case.
We have a solution to G D 0 upon taking any real K in (2.61), but the metrics
most relevant to observed phenomena are those for which K>0. Indeed, as will
be seen in 4, geodesic orbits for the metric (2.61) have the property that, for large
r and small “velocity,” they approximate orbits for the Newtonian problem
(2.62) Rx Dgrad V.x/; V.x/ D
1
2
K
jxj
:

636 18. Einstein’s Equations
If K>0, these are orbits for the Kepler problem, that is, for the two-body
planetary motion problem. If K<0, these are orbits for the Coulomb problem,
for the motion of charged particles with like charges, hence for motion under a
repulsive force. Repulsive gravitational fields have not been observed.
Note that if we take K>0in (2.61), then the formula is degenerate at r D K.
Only on fr>Kg is @=@t a timelike vector. It is this region that is properly said to
carry the Schwarzschild metric.
It follows from the fact that the sectional curvature of the plane spanned by
@=@t and @=@r is S
U
that the Schwarzschild metric (2.61) is singular at r D 0.
On the other hand, the apparent singularity in the Schwarzschild metric at r D K
actually arises from a coordinate singularity, which can be removed as follows.
First, set
(2.63) v D t C
Z
1
K
r
1
dr D t C r C K log.r K/:
Using coordinates .v;r;;'/, the metric tensor (2.61) takes the form
(2.64) ds
2
D
1
K
r
dv
2
C 2 dv dr Cr
2
d!
2
:
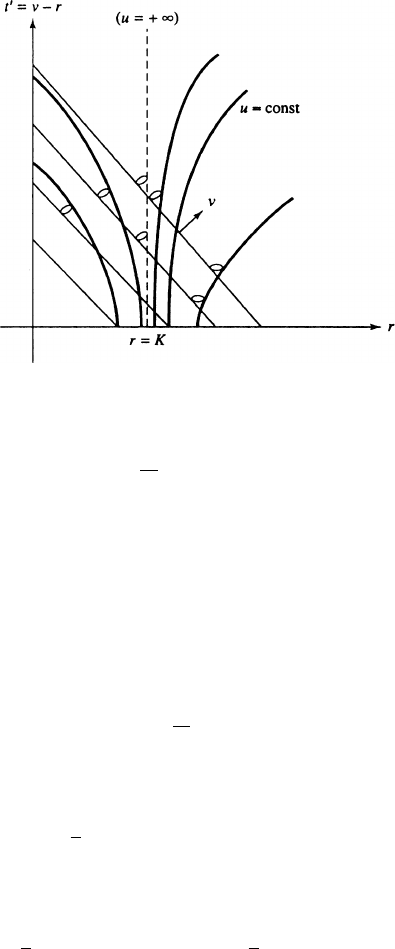
These coordinates are called Eddington–Finkelstein coordinates. The region
fr>Kg in .t;r;;'/-coordinates corresponds to the region fr>Kg in the new
coordinate system, but the metric (2.64) is smooth and nondegenerate on the
larger region fr>0g. Note that if '; ,andv are held constant and r & K,then
t %1.
The shell † Dfr D Kg is a null surface for the metric (2.64); that is, the
restriction of the metric to † is everywhere degenerate. Thus, for each p 2 †,
the light cone formed by null geodesics through p is tangent to † at p. Figure 2.1
depicts the extended Schwarzschild metric, in Eddington–Finkelstein coordinates.
The function v arises from considering null geodesics in the Schwarzschild
spacetime for which ! 2 S
2
is constant or, equivalently, considering null
geodesics in the two-dimensional spacetime
(2.65) ds
2
D
1
K
r
dt
2
C
1
K
r
1
dr
2
:
On the region r>K, there are a family of null geodesics given by v D const. and
a family of null geodesics given by u D const., where
(2.66) u D t r K log.r K/:
The coordinates .u;r;;'/ are called outgoing Eddington–Finkelstein coordi-
nates (the ones above then being called incoming), and in this coordinate system
the Schwarzschild metric takes the form
2. Spherically symmetric spacetimes and the Schwarzschild solution 637
FIGURE 2.1 Extended Schwarzschild Metric
(2.67) ds
2
D
1
K
r
du
2
2 du dr Cr
2
d!
2
:
As above, the region fr>Kg in .t;r;;'/-coordinates corresponds to the region
fr>Kg in the new coordinate system.
The incoming and outgoing Eddington–Finkelstein coordinates yield two dif-
ferent extensions of Schwarzschild spacetime. These two extensions were sewn
together by M. Kruskal and P. Szekeres. As an intermediate step from (2.64)and
(2.67) to “Kruskal coordinates,” use the coordinates .u;v;;'/. In this coordinate
system, the Schwarzschild metric becomes
(2.68) ds
2
D
1
K
r
du dv Cr
2
d!
2
;
where r is determined by
(2.69)
1
2
.v u/ D r C K log.r K/:
Now make a further coordinate change:
(2.70) D
1
2
e
v=2K
e
u=2K
;D
1
2
e
v=2K
C e
u=2K
:
Then, in the Kruskal coordinates .;;;'/, the metric becomes
(2.71) ds
2
D F.;/
2
.d
2
C d
2
/ C r.;/
2
d!
2
;
