Taylor M.E. Partial Differential Equations III: Nonlinear Equations

Подождите немного. Документ загружается.

618 18. Einstein’s Equations

Thus the condition that I.A; u/ be stationary with respect to variations of A

implies the remaining Maxwell equation:

(1.10) d

F D 4J

;

where J

is the 1-form obtained from J by lowering indices. A popular way to

write (1.9)isas

(1.11) ı

LdV D



4

C J

dV:

Furthermore, we showed that when the motion of the charged substance was

varied, leading to a variation u./ of u, with w D @



u, compactly supported, then

(1.12)

d



A; u./



D0

D

r

u 

FJ ;w

dV;

or equivalently, for the variation of the motion of the charged matter,

(1.13) ı

LdV D



u

 F



dV:

Then the condition that I.A; u/ be stationary with respect to variations of u is that

(1.14) r

u 

FJ D 0;

the Lorentz force law.

Having varied A and u in the action integral, we next vary the metric. We claim

that the variation of an action integral of the form (1.8) with respect to the metric

is given by

(1.15) ı

LdV D

.ıg

/ dV;

where T

is the stress-energy tensor associated with the Lagrangian L. We look

separately at the three terms in (1.5). First, we consider

(1.16) L

hu; ui;T

D u

To examine the variation in

dV , it is necessary to recognize that  depends

on the metric, via the identity dV D mdyds,wherem is constant. Thus

1. The gravitational ﬁeld equations 619

dV D ı

m dy ds

.ıg

/m dy ds

u

.ıg

/ dV;

(1.17)

yielding (1.15) in this case.

Next, consider

(1.18) L

D

8

hF; Fi;T

4





Now hF ; F iD.1=2/F

,and

(1.19) ı





D F



.ıg

C g

.ıg



;

while

(1.20) dV D

jgjdx H) ı.dV/ D

ıg

dV:

Hence

(1.21) 8 ı

dV D

.ıg



dV:

Using ıg

Dg

.ıg

and F

DF

, which implies F

DF

we obtain

(1.22) 8 ı

dV D

.ıg



dV;

which also yields (1.15).

For the middle term in (1.5), namely, L

DhA; J iD.e=m/hA; ui,wehave

(1.23) ı

hA; J i dV D ı

hA; ui dV D 0;

consistent with the standard choice of stress-energy tensor for the coupled system:

(1.24) T

D u

4





As noted in Chap. 2,  11, if the stationary conditions (1.10)and(1.14) are satis-

ﬁed, and (1.6)–(1.7) hold, then this tensor has zero divergence (i.e., T

D 0).

620 18. Einstein’s Equations

Now Einstein hypothesized that “gravity” is a purely geometrical effect.

Independently, both Einstein and Hilbert hypothesized that it could be captured

by adding a fourth term, L

, to the Lagrangian (1.5). The term L

should depend

only on the metric tensor on M , not on the electromagnetic or matter ﬁelds (or

any other ﬁeld). It should be “natural.” The most natural scalar ﬁeld to take is one

proportional to the scalar curvature:

(1.25) L

D ˛S;

where ˛ is a real constant.

We are hence led to calculate the variation of the integral of scalar curvature,

with respect to the metric:

Theorem 1.1. If M is a manifold with nondegenerate metric tensor .g

/,as-

sociated Einstein tensor G

D Ric

 .1=2/Sg

, scalar curvature S, and

volume element dV, then, with respect to a compactly supported variation of the

metric, we have

(1.26) ı

S dV D

ıg

dV D

ıg

dV:

To establish this, we ﬁrst obtain formulas for the variation of the Riemann

curvature tensor, then of the Ricci tensor and the scalar curvature. Let 

the connection coefﬁcients. Then ı

is a tensor ﬁeld. The formula (3.54)of

Appendix C states that if

R and R are the curvatures of the connections

r and

rC"C,then

(1.27) .R 

R/.X; Y /u D ".

C /.Y; u/  ".

C /.X; u/ C "

ŒC

u:

It follows that

(1.28) ıR

jk`

D ı

j`Ik

 ı

jkI`

Contracting, we obtain

(1.29) ı Ric

D ı

jiIk

 ı

jkIi

Another contraction yields

(1.30) g

ı Ric



ı







ı



since the metric tensor has vanishing covariant derivative. The identities

(1.28)–(1.30) are called “Palatini identities.”

Note that the right side of (1.30) is the divergence of a vector ﬁeld. This will be

signiﬁcant for our calculation of (1.26). By the divergence theorem, it implies that

1. The gravitational ﬁeld equations 621

(1.31)



ı Ric



dV D 0;

as long as ıg

(hence ı Ric

) is compactly supported.

We now compute the left side of (1.26). Since S D g

Ric

,wehave

(1.32) ıS D Ric

ıg

C g

ı Ric

Thus, since ı.dV/ is given by (1.20), we have

(1.33)

ı.S dV/ D Ric

ıg

dV C g

.ı Ric

/ dV C Sı.dV/



Ric





ıg

dV C g

.ı Ric

/ dV:

The last term integrates to zero, by (1.31), so we have (1.26).

For some purposes it is useful to consider analogues of (1.26), involving varia-

tions of the metric which do not have compact support (see, e.g., [Yo 4]and[Yo5 ]).

Note that verifying (1.26) did not require the computation of ı

in terms of

ıg

, though this can be done explicitly. Indeed, formula (3.63) of Appendix C

implies

(1.34) ı

`j k

ıg

`j Ik

 ıg

`kIj

C ıg

jkI`

From Theorem 1.1 together with (1.15), we see that if L is a matter Lagrangian,

such as in (1.5), then the stationary condition for

(1.35) ı



S C 8L



dV;

with respect to variations of the metric tensor, yields the gravitational equation

(1.1).

An alternative formulation of (1.1) is the following. Take the trace of both sides

of (1.1). We have

(1.36) G

D Ric



1 



when n D dim M .Sincen D 4 here, this implies

(1.37) S D 8;  D T

Then substitution of 8 for S in (1.1) yields

(1.38) Ric

D 8



g



622 18. Einstein’s Equations

We now derive a geometrical interpretation of the Einstein tensor. Let  D e

be any unit timelike vector in T

M , part of an orthonormal basis fe

of T

M ,wherehe

iDC1 for j  1; 1 for j D 0. From the deﬁniton of

the Ricci tensor, we obtain

(1.39) Ric.; / D

j D1

R.e

;/;e

D

j D1

K. ^ e

where K. ^ e

/ denotes the sectional curvature with respect to the 2-plane in

M spanned by  and e

. Compare with Proposition 4.7 of Appendix C, but

note the sign change due to the different signature of the metric here. Also, the

scalar curvature of M at p is given by

(1.40) S D

j ¤k

K.e

^ e

/.0 j; k  3/:

Hence, for G D Ric  .1=2/Sg,wehave

(1.41) G.; / D Ric.; / C

S D

1j<k

K.e

^ e

Now let V



be the spacelike hypersurface, formed by the geodesics through p

normal to . The second fundamental form of V



vanishes at p (see the proof of

Proposition 4.7 in Appendix C, analyzing the sectional curvature). It follows that

the scalar curvature of V



at p is given by

(1.42) S.V



/ D 2

1j<k

K.e

^ e

with K.e

^ e

/ as in (1.41). Hence

(1.43) S.V



/ D 2G.; /:

Thus the gravitational equation (1.1) can be written as

(1.44) S.V



/ D 16;

where

(1.45)  D T.;/

is the energy density, measured by an observer with 4-velocity . Note that if T

is given by (1.3), then T.;/ D hu;i

, which is nonnegative (in fact, positive

where  ¤ 0). Also, if T is the stress-energy tensor (1.4) of the electromagnetic

1. The gravitational ﬁeld equations 623

ﬁeld, then, as observed in calculations leading to (11.33) in Chap. 2, T.;/is the

observed measurement of .1=8/



jEj

CjBj



, also nonnegative (and positive

where the electromagnetic ﬁeld does not vanish). Typically, a stress-energy tensor

for ordinary matter has the property that

(1.46) T.;/  0; for  timelike.

If >0at p, we see that S.V



/ has the same sign as the constant .Belowwe

will argue that  is positive.

Note that the equation (1.14) indicates that uncharged matter should move

along geodesics. Let us consider the inﬂuence of the geometry on the rela-

tive motion of nearby neutral particles, whose motion is along nearby timelike

geodesics in M . Say one geodesic 

.s/ has unit timelike tangent vector  D



.s/Ih; iD1. If there is a one-parameter family of geodesics 



.s/,then

W.s/ D @







.s/

D0

is a vector ﬁeld along 

that satisﬁes the Jacobi equation

(1.47) r



W D R.; W /:

See Exercise 10 in  3 of Appendix C.

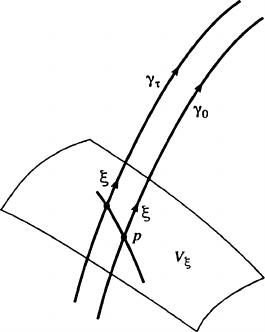
Let us vary the geodesic 

in the following speciﬁc fashion. Let V



the hypersurface described above, spanned by geodesics through p D 

.0/

with tangent vector in ./

 T

M .Weextend over V



by radial paral-

lel transport and, given q 2 V



, close to p, consider the geodesic  satisfying

.0/ D q; 

.0/ D  (see Fig. 1.1). If 



is a one-parameter family of such

geodesics, with W.s/ D @







.s/

D0

,then

(1.48) W.0/ ?  2 T

M and r



W.0/ D 0:

FIGURE 1.1 Nearby Timelike Geodesics

624 18. Einstein’s Equations

Note that .d=ds/hW; iDhr



W;i and

hW;iDhr



W;iD

R.; W /;

D 0:

Hence, if (1.48) holds, then W.s/ ? .s/ all along 

Now we have .d=ds/hW; W iD2hr



W;W i,and

(1.49)

hW;W iD2



W;W iD2hr



W;W iC2hr



W;r



W i:

Hence, at p,

(1.50)

hW;W iD2hR.W; /; W i:

If we let W

be an orthonormal basis of T



/, we obtain, via (1.39),

(1.51)

j D1

iD2 Ric.; / D16

T.;/C



;

at p.

Note that if T is given by (1.3), then

(1.52) T.;/C

 D h; ui

hu; ui0;

when  and u are both unit timelike vectors. In particular, T.u; u/C=2 D =2,in

this case. Generally, a stress-energy tensor T is said to satisfy the “strong energy

condition” if T.;/ C =2  0 for all unit timelike . For such stress-energy

tensors, we have (at p)

(1.53)

j D1

i0 if >0;

D 0 if  D 0;

 0 if <0:

Now, it is clear that an attractive gravitational force would make (1.53)  0 (and

in fact <0in a nontrivial matter ﬁeld), while a repulsive force would make (1.53)

 0. Since we observe gravity to be attractive, we conclude that the constant  in

(1.1)is>0. Further discussion of the determination of  will be given in  6,after

(6.73)–(6.74).

Exercises 625

Exercises

1. If M is a Riemannian manifold of dimension 2, show that G

D 0. Deduce from

Theorem 1.1 that

(1.54)

KdAD C.M/

is independent of the metric on M . Relate this to the Gauss–Bonnet formula established

in  5 of Appendix C, on connections and curvature.

2. As shown in (3.31) of Appendix C, the Einstein tensor satisﬁes

(1.55) G

D 0;

as a consequence of the Bianchi identity. Hence, Einstein’s equations (1.1)imply

(1.56) T

D 0:

Compute this when T

is given by (1.24). Compare with the calculation (11.54) of

Chap. 2.

3. A ﬂuid, with 4-velocity ﬁeld u (satisfying hu; uiD1), density , and pressure p

(measured by an observer with velocity u), has stress-energy tensor

(1.57) T

D . C p/u

C pg

Thus a dust, with the stress-energy tensor (1.3), is a zero-pressure ﬂuid. Compute T

in this case, and show that the conservation law (1.7) and the geodesic equation r

u D 0

(which is (1.14) in the absence of an electromagnetic ﬁeld) are modiﬁed to

(1.58) div.u/ Dp div u;.Cp/r

u D….u/ grad p;

where ….u/ denotes projection orthogonal to u (with respect to the Lorentz metric),

namely, in components, .….u/ grad p/

D p

C u

4. Recall from (1.37) that when (1.1) holds, the scalar curvature of spacetime is given by

S D8T

. Deduce that if T

isgivenby(1.24), then

(1.59) S D 8;

while if it is given by (1.57), then

(1.60) S D 8.  3p/:

5. Show that if T

is given by (1.3), then

(1.61) Ric.u; u/ D 4;

and if it is given by (1.24), then

(1.62) Ric.u; u/ D 4 C .jEj

CjBj

626 18. Einstein’s Equations

where E and B are the electric and magnetic ﬁelds, measured by an observer with

4-velocity u, while if it is given by (1.57), then

(1.63) Ric.u; u/ D 4. C 3p/:

2. Spherically symmetric spacetimes and the Schwarzschild

solution

We investigate solutions to Einstein’s equations (1.1) which are spherically sym-

metric. Generally, a Lorentz 4-manifold .M; g/ is said to be spherically symmetric

provided there is an effective action of SO.3/ as a group of isometries of M .The

generic orbit O will be diffeomorphic to S

. We will assume that O is spacelike,

that is, the metric induced on O is positive-deﬁnite. Given p 2 O,letK

be the

subgroup of SO.3/ ﬁxing pI K

is a circle group. Thus K

acts as a group of

rotations on T

O, and it also acts on N

O D T

.SinceN

O has a metric of

signature .1; 1/,andK

acts on it as a compact, connected group of isometries,

it follows that K

acts trivially on N

On a neighborhood of O  M , diffeomorphic to .a; b/  .c; d /  S

, we can

introduce coordinates so that the metric is

(2.1) ds

DC.r;t/dt

C D.r; t/ dr

C 2E.r; t/ dr dt C F.r;t/d!

;

Where the functions C;D;E,andF are smooth and positive, and d!

is the

standard Riemannian metric on the unit sphere, S

 R

. Assume that @F =@r ¤

0 on O. Then we can change variables, replacing r by r

F.r;t/, and get the

simpler form

(2.2) ds

DC.r;t/dt

C D.r; t/ dr

C 2E.r; t/ dr dt C r

;

with new functions C.r;t/, and so on. Next, we can replace t by t

, such that

(2.3) dt

D .r; t/



C.r;t/dt E.r;t/ dr;

where .r; t/ is an integrating factor, chosen to be positive and to make the right

side of (2.3) a closed form. Then the metric on M takes the form

(2.4) ds

De

.r;t/

C e

.r;t/

C r

We take spherical coordinates .'; / on S

,where' D 0 deﬁnes the north pole

and ' D =2 deﬁnes the equator. (Physics texts often give ' and  the opposite

roles.) Then

D d'

C sin

'd

2. Spherically symmetric spacetimes and the Schwarzschild solution 627

The formula for the Einstein tensor G

for such a metric is fairly complicated.

Rather than just write it down, we will take a leisurely path through the calcu-

lation, making some general observations about the Einstein tensor, and other

measures of curvature, along the way. Some of these calculations will have fur-

ther uses in subsequent sections. Among alternative derivations of the formula for

the Ricci tensor for a metric of the form (2.4), we mention one using differential

forms, on pp. 87–90 of [HT].

The metric (2.4) has the general form

(2.5) g

D g

C g

; 2 C

.U /;

on a product M D U  S,whereg

is the metric tensor of a manifold U; g

themetrictensorofS.Tobemoreprecise,if

/ D .x

;:::;x

L1

;:::;x

LCM 1

/ 2 U  S;

is the metric tensor for U if 0  j; k  L1,andweﬁlling

to be zero for

other indices. Similarly, we set g

D h

j CL;kCL

for 0  j; k  M  1,where

is the metric tensor for S,andweﬁlling

to be zero for other indices.

In the example (2.4), we have U  R

;SD S

,soL D M D 2. With obvious

notation,

(2.6) g

D g

1

We want to express the curvature tensor R

k`m

of M in terms of the tensors

k`m

and

k`m

and the function and then obtain formulas for the Ricci

tensor, scalar curvature, and Einstein tensor of M . Recall that if 

are the

connection coefﬁcients on M ,then

(2.7) R

k`m

D @



 @



C 

`





 

m





;

where we use the summation convention (sum on ). Meanwhile,

(2.8) 

`



j

C @

k

 @





Using (2.5)and(2.6), we can ﬁrst express 

in terms of the connection coefﬁ-

cients on the factors U and S:

(2.9) 



C B

;