Taylor M.E. Partial Differential Equations III: Nonlinear Equations

Подождите немного. Документ загружается.

668 18. Einstein’s Equations

Now u

D @

C 

,where

isgivenby(2.9). When u has the form

(6.61), then u

D u

D .@

C 

. Also, by (2.9), 



C B

, and by (2.10), B

D 0, while (2.43) implies

(6.68)



D 0;







Thus, when u has the form (6.61),

(6.69) u





Now, in the static, spherically symmetric case,  D .r/ and p D p.r/, so clearly

. Cp/ D u

. Cp/ D 0, and the only nontrivial component of the left side

of (6.67)is

(6.70) T

. C p/

.r/e



C p

.r/e



Thus we again derive (6.66).

We can use (6.66) to eliminate 

from the second equation in (6.63). The

result, together with the ﬁrst equation in (6.63), gives a 2 2 system for .r/ and

p.r/:

(6.71)



.r/ D

1  e



 8re



;

p C 

.r/ D

1  e



 8re



under the hypothesis that  D .p/. It is common to replace .r/ by a function

giving the metric (6.60) a form more resembling (2.61). We deﬁne M.r/ by

(6.72) e

.r/



1 

2M.r/



1

;

so that M.r/ D r.1  e



/=2. The system (6.71) takes the form

(6.73) M

.r/ D 4r

; p

.r/ D

.p C /.M C 4r

r.r  2M /

;

known as the Oppenheimer–Volkov equation.

In the Newtonian limit, p<<;4r

p<<M,and2M << r,andthese

equations become

(6.74) M

.r/ D 4r

; p

.r/ D

M

Exercises 669

In fact, this is precisely the equation for a static ﬂuid in Newtonian mechanics, in

which the force of gravity exactly balances the force due to the pressure gradient.

In such a case, M.r/ is the gravitational mass of the matter enclosed in the ball

fjxjrgin R

. The relation between density and gravitational mass, given by the

ﬁrst equation of (6.74) (in the limit when Newtonian mechanics applies) serves to

identify the constant  in Einstein’s equation (1.1), with the gravitational constant

of Newtonian theory.

The Oppenheimer–Volkov system (6.73) has consequences signiﬁcantly dif-

ferent from the Newtonian approximation (6.74), for very dense objects. For

example, it leads to theoretical upper bounds on the mass of a stable neutron star

which are stronger than those obtainable from (6.74). Discussions of this can be

found in [Str,Wa,Wein].

In treating (6.73), it is natural to set M.0/ D 0 and let p.0/ D p

run over a

range of values. We assume that p

./ > 0 in the equation of state, so  D .p/

in (6.73), with 

.p/ > 0. Despite the vanishing of the denominator in the second

equation of (6.73)atr D 0, there is no real singularity there. Indeed, one easily

veriﬁes that

(6.75)

M.r/ D

4



C O.r

p.r/ D p



2

C 

/.3p

C 

C O.r

with 

D .p

/. For a numerical treatment of (6.73), it is convenient to use (6.75)

for r very small, and then use a difference scheme, to produce an approximate

solution for larger r.

Exercises

1. Assume u.p/ ¤ 0 and W.p/ ¤ 0.Using(6.42), show that the linear span L

of u.p/

and W.p/ is given by

Dfv 2 T

M W 

 D 0g:

Using (6.32), show that the resulting subbundle L of TM is invariant under the ﬂow

generated by u (in regions where u and W are both nonvanishing). In light of this,

derive analogues of the Kelvin and Helmholtz theorems, established for nonrelativistic

ﬂuids in  5 of Chap. 16 and  1 of Chap. 17.

2. Consider a static, spherically symmetric, charged ﬂuid and associated electromagnetic

ﬁeld. Discuss the equations of motion.

3. Compute the second terms in the power-series expansions of M.r/ and of p.r/ about

r D 0 in (6.75), namely, the coefﬁcients of r

and of r

, respectively.

4. Write some computer programs to solve numerically the Oppenheimer–Volkov system

(6.73), with initial data M.0/ D 0; p.0/ D p

. Try various equations of state, such as

(6.76) p./ D k

4=3

;

670 18. Einstein’s Equations

with k D const., used in models of white dwarf stars. For another example, ﬁx 

.0; 1/, and use

(6.77)

p./ D

; for   

;

p./ D k

4=3

; for   

;

with k picked so 

=3 D k

4=3

(i.e., k D 

1=3

=3).

See [Str]and[Wein] for discussions of variants of (6.77) used in models of neutron

stars.

5. Suppose the equation of state were

(6.78) p./ D



for all  2 R

. Produce a solution to (6.73)oftheform

(6.79) M.r/ D Ar; p.r/ D Br

1

;

for certain constants A; B. Relate this to the assertion that (6.78) cannot be a realistic

equation of state at low density.

7. Gravitational collapse

In many cases, solutions to Einstein’s equations, particularly coupled to matter,

develop singularities in ﬁnite time, sometimes as part of the phenomenon of grav-

itational collapse. We begin this section with some simple examples in which

gravitational collapse occurs.

Let us consider a homogeneous, isotropic universe, containing a ﬂuid with

uniform density and pressure. We write the metric as

(7.1) ds

Ddt

C A.t/g

;

where g

is a constant-curvature metric on a 3-manifold S . The stress-energy

tensor has the form (6.2), with

(7.2)  D .t/; p D p./; u D .1;0;0;0/:

We can compute the Einstein tensor of this metric using formulas from  2.We

have M D U  S , where dim U D 1 and dim S D 3.From(2.22)wehave

(7.3) Ric

D Ric

C F

;

and F

isgivenby(2.28), with # D log A.t/. Hence (keeping in mind (2.20))

we have

(7.4) F

D

2



;

7. Gravitational collapse 671

and, for 1  j; k  3,

(7.5) F

D

1

AA



By (2.29), the scalar curvature of M is

(7.6) S D A

1

C ˇ;

where

(7.7) ˇ D g

D 3A

1

Then, by (2.36), the Einstein tensor of M is given by

(7.8) G

D G

1

C F



ˇg

In particular,

(7.9) G

1

C F

ˇ D

1

;

and, for 1  j; k  3,

(7.10) G

D G

C F



D G



1

Now, if S has constant sectional curvature (and hence constant scalar curvature

), then

Ric

must be a scalar multiple of ı

, and the multiple must be

=3,so

(7.11) G

D

If T

is given by (7.2), then Einstein’s equations yield the following pair of

equations for A.t/ and .t/:

(7.12)





D 8;



D8Ap./:

672 18. Einstein’s Equations

To put this in a slightly different form, we set A.t/ D R.t/

and note that if S has

constant sectional curvature K,thenS

D 6K. The we can rewrite (7.12)as

(7.13)

C K D

R

;

2RR

C .R

C K D8p./R

It is useful to perform some elementary operations on these equations. Note that

taking the difference yields

(7.14) 3

D4. C 3p/;

while multiplying the ﬁrst equation in (7.13) by 3 and taking the difference yields

(7.15)





 4. C p/:

On the other hand, applying d=dt to the ﬁrst part of (7.13)gives

(7.16)

d

D6K

C 6





;

and substituting (7.15)into(7.16)thengives

(7.17)

.R

/ Dp

One can also deduce (7.17) from the identity T

D 0 (with j D 0), in a fashion

analogous to the derivation of (6.66)via(6.67)–(6.70). In turn, (7.17) implies the

relation

(7.18)

D

d

 C p./

;

which gives R as a function of ,or as a function of R.

Let us ﬁx R

D R.t

/ and 

D .t

/. We can now regard (7.14) as a dynam-

ical equation for R:

(7.19) R

D

'.R/; '.R/ D . C 3p/R ;

given  and p./ as functions of R, and then the ﬁrst part of (7.13) can be regarded

as the conservation law:

(7.20)



 .R/ DK; .R/ D R

7. Gravitational collapse 673

In other words, if we write (7.19) as a ﬁrst-order system:

(7.21) R

D V; V

D

'.R/;

then the orbits lie on level curves

(7.22) F.V;R/ DK; F.V; R/ D



 .R/:

Thus we will examine these level curves.

To do this, we look at (7.18), which gives

(7.23) R D R

./=3

;./D



d

 C p./

If we assume that the equation of state satisﬁes

(7.24) p.0/ D 0; p

./  1;

then (if say 

D 1)for  1,wehave.1=2/ log  ./  log ,

so R



1=3

 R  R



1=6

, with reversed inequalities for   1. Hence

=R/

   .R

=R/

for   1,so .R/ has the property

(7.25) R  R

 .R/ 

Similarly,

(7.26) R  R

 .R/ 

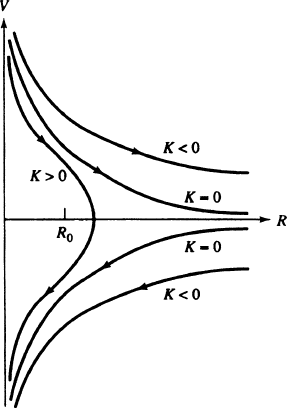
In Fig. 7.1 we depict the level curves of F.V;R/and the resulting phase-plane

portrait of the system (7.21). Note that all the orbits .R.t/; V .t// in the region

V<0have the property R.t/ & 0; V .t/ &1,ast increases. In particular, if

V.t

/<0,thenR

.t/ is bounded away from zero for t  t

,soR.t/ must reach

zero at a ﬁnite time t

Š Similarly, if V.t

/>0,thenR.t/ must vanish for

some ﬁnite t<t

. Of course, at R D 0;  DC1, and the metric is singular. If

K>0, one must have a singularity both at a ﬁnite time before t

and at a ﬁnite

time after t

.IfK  0, there must be such a singularity either at some ﬁnite t<t

or at some ﬁnite t>t

That such complete collapse must occur is not surprising in the case of a dust,

where p D 0. However, it is striking that, given any realistic equation of state, the

pressure cannot prevent the collapse to inﬁnite density, even in the case K>0

and the total amount of matter in the universe is ﬁnite.

674 18. Einstein’s Equations

FIGURE 7.1 Orbits for (7.21)

One can cut and paste a portion of some of the spacetimes described above with

a portion of Schwarzschild spacetime to give a model of collapse of a star, with

spherical symmetry. The collapse of a rotating star is much more complicated. For

further discussion, see [MS] and references given therein. It is worth mentioning

the widely held belief that such a collapse, generally accompanied by gravitational

radiation, should rapidly approximate a Kerr solution.

There are a number of general results on the inevitability of gravitational col-

lapse, accompanied by singularity formation. A detailed treatment is given in

[HE], and we mention only one relatively simple case here. We show that un-

der certain mild conditions, an irrotational dust must give rise to a singularity in

spacetime. We begin with a pair of geometrical lemmas.

Lemma 7.1. If u is a vector ﬁeld satisfying

(7.27) hu; uiD1; r

u D 0; A

D A



;

then

(7.28) L

.div u/ DRic.u; u/  Tr A

Proof. Let fe

W 1  j  3g be a local orthonormal frame ﬁeld for †, the bundle

of 3-planes orthogonal to u.Then(6.16) yields

(7.29) L

.div u/ Dhr

u;e

iChr

u; r

7. Gravitational collapse 675

Here and below, we use the summation convention. Now write the ﬁrst term on

the right side of (7.29)as

(7.30)

u;e

iDhr

u;e

iChr

Œu;e



u;e

iChR.u;e

/u;e

DhA

Œu;e

; e

i Ric.u; u/;

using r

u D 0.IfA

D A



,wehave

(7.31)

u; r

ihA

Œu;e

; e

iDhA

; r

C Œu;e

i

DhA

i2hA

; r

since Œu;e

 Dr

r

The expression hA

i (summed over j ) is equal to Tr A

if A



.Furthermore,

; r

iDA

; r

where .A

/ is the matrix of A

, with respect to the basis fe

g, which is symmet-

ric. Since he

; r

i is antisymmetric in .j; k/, we deduce that hA

; r

iD0

(summed over j ). This proves (7.28).

Recall from Lemma 6.1 that A

D A



is an integrability condition, and, by

Lemma 6.2, it is equivalent to vanishing vorticity. Note that if A

D A



,then

Tr A



.Tr A

;

as can be seen by putting A

in diagonal form. Using (6.15), we can deduce the

following:

Lemma 7.2. Under the hypotheses of Lemma 7.1,

(7.32) L

.div u/ 

.div u/

 Ric.u; u/:

Proposition 7.3. Suppose M is a spacetime containing a dust, so the Einstein

equations hold, with T

given by

(7.33) T

D u

;

with   0 and hu; uiD1. Assume that the motion of the dust is irrotational.

Finally, assume that, for some p 2 M ,

(7.34) div u.p/ Db<0:

676 18. Einstein’s Equations

Let  be the orbit of u (a unit-speed geodesic) such that .0/ D p.If./ is

deﬁned for  2 Œ0; a/,thena  3=b.Furthermore,ifa D 3=b,then

(7.35) 



./



!C1 and S



./



!C1; as  % a:

Proof. Under our hypotheses, Corollary 7.2 applies, so we have (7.32). Also, by

(1.61),

(7.36) Ric.u; u/ D 4;

which is  0. Hence,

(7.37) f./ D div u..// H) f

./ 

f./

;

so the hypothesis (7.34) implies

(7.38) f./ 

3  b

;

for 0  <a, provided f./is smooth on Œ0; a/. This shows that a  3=b.Also,

if a D 3=b,thenf./ !1as  % a,insuchafashionthat

(7.39)

f./d D1:

To conclude the proof of (7.35), note that, given a dust, by (6.5)wehave

div.u/ D 0, hence L

 C  div u D 0,or

.log / Ddiv u; i.e.,

d

log ..// Df./:

Hence (7.39) implies the ﬁrst part of (7.35). By (1.59)wehave

S D 8;

so the second part of (7.35) also holds.

Exercises

1. Obtain more explicit solutions to (7.13) for a dust (i.e., when p D 0). (Hint:Use(7.17).)

2. Assume p D 0.LetM have a metric of the form (7.1), by solving (7.12). Let B be

a ball in the 3-manifold S,usedin(7.1), and let  be the subset of M formed by

timelike geodesics through @B , orthogonal to S .Glue to an appropriate piece of

Schwarzschild spacetime (whose boundary is also swept out by timelike geodesics)

so as to model the collapse of a dust ball. In what sense do (6.1)and(6.2)holdona

neighborhood of the interface?

8. The initial-value problem 677

3. Consider the behavior of a homogeneous, isotropic universe ﬁlled with a uniform ﬂuid

(i.e., consider solutions to (7.12)), when one does not require that the equation of state

satisfy p

./  1.

8. The initial-value problem

To begin, we look at the initial-value problem for the empty-space Einstein equa-

tions, which can be written as

(8.1) Ric

D 0:

In our ﬁrst formulation of the initial-value problem, we try to prescribe, on a

3-dimensional surface S Dfx

D 0gM , the initial data

(8.2) g

Here, @

D @=@x

.TakeM open in R

;SD M \fx

D 0g. We will see shortly

that compatibility conditions will be required on these data. In local .x

;:::;x

coordinates we have

(8.3)

Ric



@

 @

C @



C M

.g; rg/

D L

.g; D/g CM

.g; rg/:

Now it is easy to see that S Dfx

D 0g is characteristic for L. This results

from the coordinate independence of the condition (8.1). We can get around this

problem by choosing coordinate systems of a special nature.

One way to do this is the following, used by [CBr2], following [Lan]. Rewrite

(8.3)as

(8.4) Ric

D



C H

.g; rg/;

where

(8.5) 

D g





C @

 @



;

and the 

are the Christoffel symbols for the metric tensor .g

/, in the coordi-

nates .x

;:::;x

/.If is the Laplace–Beltrami operator deﬁned by the Lorentz

metric .g

/,then

(8.6) u D g

Ij Ik

D g

u  