Суляндзига Е.П., Ушакова Г.А. Тесты по математике: Предел, производная, элементы алгебры и геометрии
Подождите немного. Документ загружается.


63
2) Если коэффициенты
A
и
B
не равны (
A B
≠
), но имеют одинако-
вые знаки, то уравнение описывает эллипс;
3) Если коэффициенты
A
и
B
не равны (
A B
≠
) и имеют разные зна-
ки, то уравнение описывает гиперболу;
4) Если один и коэффициентов
A
или
B
равен нулю (
0
A
=
или
0
B
=
),
т.е. отсутствует слагаемое, содержащее квадрат переменной
x
или
y
, то
такое уравнение описывает параболу.
Кривые, заданные уравнением
2 2
0
Ax By Cx Dy E
+ + + + =
, имеют
смещенные оси симметрии, а значит и центр симметрии или координаты
вершин.
Пример 44.
Установите вид кривой
2 2
2 2 8 3 0
x y x y
− + − − + =
и по-
стройте график.
Решение
Уравнение
2 2
2 2 8 3 0
x y x y
− + − − + =
описывает гиперболу: коэффици-
енты
,
A B
имеют разные знаки,
A B
≠
,
1, 2
A B
= − =
.
Выделим полные квадраты по переменным
,
x y
. Очевидно, что для пе-
ременной
x
получим квадрат суммы, а для переменной
y
−
квадрат разно-
сти:
( ) ( )
( ) ( )
( ) ( ) ( ) ( )
( )
( )
2 2 2 2
2 2
2 2
2 2 2 2
2 2
2 2 8 3 0 2 2 8 3 0
2 2 4 3 0
2 1 1 2 4 4 4 3 0
1 1 2 2 8 3 0 1 2 2 4
1 2
1.
4 2
x y x y x x y y
x x y y
x x y y
x y x y
x y
− + − − + = ⇔ − − + − + = ⇔
⇔ − + + − + = ⇔
⇔ − + + − + − + − + = ⇔
⇔ − + + + − − + = ⇔ − + + − = ⇔
+ −
⇔ − + =
Итак, получили уравнение гиперболы:
( ) ( )
2 2
1 2
1
4 2
x y+ −
− + =
Выполним параллельный перенос системы координат, начало новой
системы координат
1 1 1
x O y
– это точка
(
)
1
1, 2
O
−
.
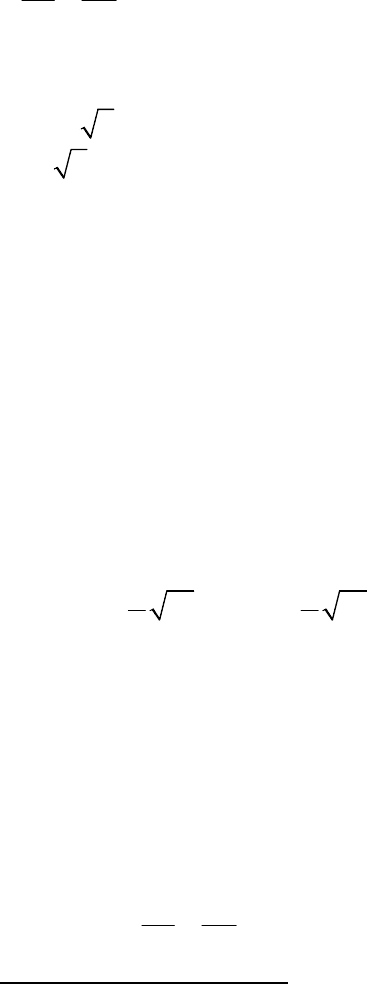
Введем обозначения:
1 1
1 ; 2
x x y y
+ = − =
. Уравнения новых координат-
64
ных осей
13
1 1 1 1
,
O x O y
имеют вид:
1
1
0,
0.
y
x
=
=
Относительно старой систе-
мы координат
xOy
новые оси записываются уравнениями:
1
1
0,
2 0; 2;
0 1 0 1.
y
y y
x x x
=
− = =
⇔ ⇔
= + = = −
Начало новой системы координат – точка с координатами:
(
)
1
1; 2 .
O
−
В
новой системе координат
1 1 1
x O y
заданное уравнение принимает канони-
ческий вид:
2 2
1 1
1.
4 2
x y
− + =
Анализируя полученное каноническое уравнение
, можно сказать, что
график этой гиперболы ось
1 1
O x
не пересекает, ось
1 1
O y
пересекает в
точках
2.
±
Следовательно, мнимая полуось
2
a
=
, действительная полу-
ось
2
b =
.
Для упрощения построения искомого графика найдем точки пересече-
ния графика заданной гиперболы с координатными осями системы
xOy
.
Точки пересечения графика гиперболы с осью
:
Ox
( )
2 2
2
2
2
2 2 8 3 0,
2 3 0
0
2 3 0 1 4 1 2 3, 1.
x y x y
x x
y
x x x x x x
− + − − + =
⇔ − − + = ⇔
=
⇔ + − = ⇔ + = ⇔ + = ± ⇔ = − =
Точки пересечения графика гиперболы с осью
:
Oy
2 2
2
2 2 8 3 0,
2 8 3 0
0
1 1
y 4 10; y 4 10.
2 2
x y x y
y y
x
− + − − + =
⇔ − + = ⇔
=
⇔ = − = +
Приступаем к построению графика заданного уравнения гиперболы.
Вся нужная информация имеется:
1. В старой системе координат
xOy
строим прямые
1, 2
x y
= − =
. Это
новые оси
1 1
O y
и
1 1
O x
координатной системы
1 1 1
x O y
соответственно. Нача-
ло координат
1 1 1
x O y
−
точка
(
)
1
1, 2
O
−
.
2. В новой системе координат
1 1 1
x O y
имеем каноническое уравнение
гиперболы
2 2
1 1
1.
4 2
x y
− + =
Мнимая полуось
2
a
=
, действительная полуось
13
Уравнения координатных осей в системе
:
xOy
ось
:
Ox
0
y
=
, ось
:
Oy
0
x
=
.
65
2
b =
.
3. В новой системе координат
1 1 1
x O y
строим прямоугольник со сторо-
нами
2 4
a
=
и
2 2 2
b =
, центр симметрии – начало координат
(
)
1
1;2
O
−
,
проводим диагонали – асимптоты гиперболы. Кстати спросить, уравнения
асимптот можно записать?
4. Зная, что гипербола, каноническое уравнение которой получили, ось
1 1
O x
не пересекает, а вершины находятся на оси
1 1
O y
в точках
2
±
, легко
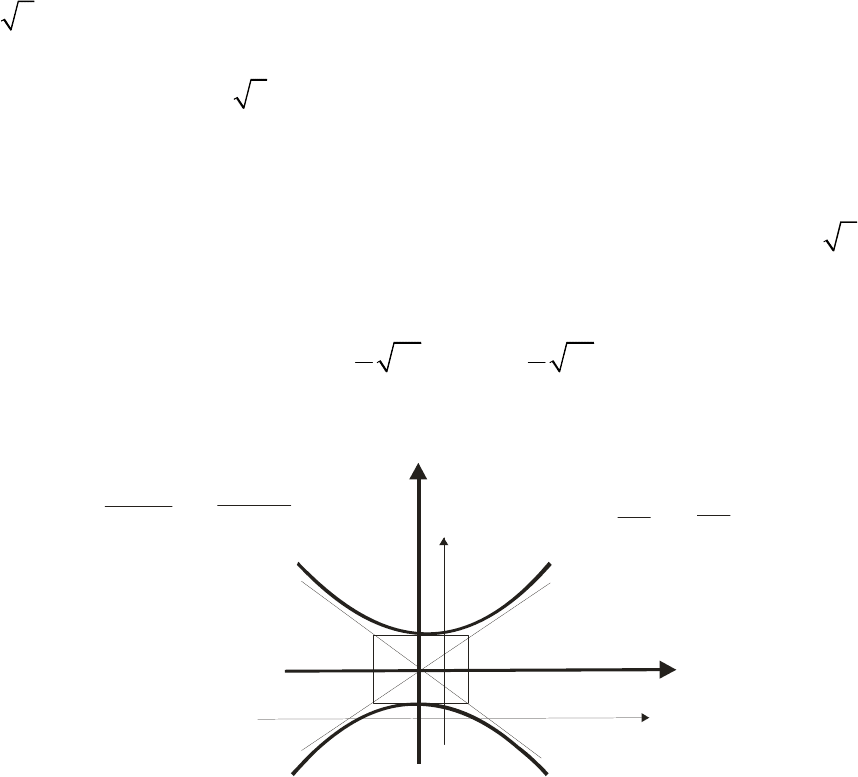
построить искомую кривую (рис. 14). При этом для точности построения
надо учесть точки пересечения графика гиперболы со старыми осями ко-
ординат:
3, 1
x x
= − =
и
1 1
y 4 10; y 4 10
2 2
= − = +
.
2
2
x
x
x
x +1
y - 2
y
y
y
-
-
=1
a=1,4
b=2 -
- полуось,
полуось
мнимая
действительная
+
1
1
11
2
2
2
-2
4
4
2
2
1
(
(
) )
+
=
Рис. 14. График линии, заданной уравнением
2 2
2 2 8 3 0
x y x y
− + − − + =
Пример 45.
Установите вид кривой для каждого из следующих рав-
нений:
1.
2 2
4 9 40 36 100 0,
x y x y
+ − + + =
2.
2 2
9 16 54 64 127 0,
x y x y
− − − − =
3.
2
9 18 4 45 0,
x x y
+ − + =
4.
2 2
4 2 8 3 0,
x y x y
− + − + + =
5.
2 2
2 2 8 6 42 0,
x y x y
+ + − + =
66
6.
2
2 4 4 2 0,
y x y
+ − − =
7.
2 2
4 0,
x y
− =
8.
2 2
2 4 1 0.
x y x y
+ − + + =
Решение
1.
2 2
4 9 40 36 100 0
x y x y
+ − + + =
−
уравнение эллипса, коэффициен-
ты
,
A B
имеют одинаковые знаки,
4, 9
A B
= =
,
A B
≠
;
2.
2 2
9 16 54 64 127 0
x y x y
− − − − =
−
уравнение гиперболы, коэффици-
енты
,
A B
имеют разные знаки,
A B
≠
,
9, 16
A B
= = −
;
3.
2
9 18 4 45 0
x x y
+ − + =
−
уравнение параболы, коэффициенты
9, 0
A B
= =
;
4.
2 2
4 2 8 3 0
x y x y
− + − + + =
−
уравнение гиперболы, коэффициенты
,
A B
имеют разные знаки,
A B
≠
,
1, 4
A B
= − =
;
5.
2 2
2 2 8 6 42 0
x y x y
+ + − + =
−
уравнение окружности, коэффициен-
ты
,
A B
имеют одинаковые знаки,
2, 2
A B
= =
,
A B
=
;
6.
2
2 4 4 2 0
y x y
+ − − =
−
уравнение параболы, коэффициенты
0, 2
A B
= =
;
7.
2 2
4 0
x y
− =
−
уравнение второго порядка выродилось в два ли-
нейных:
( )( )
2 2
2 0
4 2 2 0
2 0
x y
x y x y x y
x y
− =
− = − + = ⇔
+ =
. Кривая второго по-
рядка выродилась в две пересекающиеся и проходящие через начало
координат прямые;
8.
2 2
2 4 1 0.
x y x y
+ − + + =
Хочется сказать, что данное уравнение
описывает окружность:
1
A B
= =
. Выполним эквивалентные преобразо-
вания:
( ) ( )
( ) ( )
2 2 2 2
2 2
2 2
2 4 9 0 2 1 1 4 4 4 9 0
2 1 1 4 4 4 9 0 1 2 4 0.
x y x y x x y y
x x y y x y
+ − + + = ⇔ − + − + + + − + = ⇔
⇔ − + − + + + − + = ⇔ − + + + =
Равенство
( ) ( )
2 2
1 2 4 0
x y
− + + + =
на плоскости действительных чисел
R
2
является ложным. Это мнимая окружность.

67
9. ОПРЕДЕЛИТЕЛИ. РАНГ МАТРИЦЫ.
Пример 46
. Укажите, сколько решений имеет система линейных
уравнений, записанная в матричном виде
1 0 1 1
2 1 1 0
1 1 2 1
x
y
z
−
⋅ =
?
Ответы
:
три решения;
единственное решение;
не имеет решений;
бесконечное множество.
Решение
Матрица системы
1 0 1
2 1 1
1 1 2
A
−
=
,
1 0 1 1
2 1 1 0
1 1 2 1
B
−
=
−
расширенная
матрица системы.
Исследуем матрицу
A
. Для нее можно построить только один опреде-
литель 3-го порядка. Вычислим его:
1 0 1 1 0 0
det 2 1 1 2 1 3 0
1 1 2 1 1 3
A
−
= = =
.
Поскольку
det 0
A
=
, а
det
A
−
это определитель 3-го порядка, то ранг
14
матрицы
(
)
r A
не может быть равен 3, он может быть только меньше трех,
т.к. для матрицы
A
нельзя построить другой определитель 3-го порядка.
Итак,
(
)
3
r A
<
.
Рассмотрим какой-либо определитель 2-го порядка, порожденный мат-
рицей
A
. Пусть будет определитель
1 0
2 1
. Элементы, его образующие,
стоят на пересечении первых двух строк и первых двух столбцов. Очевид-
но что
1 0
1,
2 1
=
т.е. нашли отличный от нуля определитель 2-го порядка, а
это значит, что ранг матрицы
A
равен 2,
(
)
2
r A
=
.
14
Ранг матрицы – это наибольший из порядков отличных от нуля определителей, порожденных
матрицей. Ранг матрицы
A
обозначим
(
)
r A
.
68
Исследуем расширенную матрицу
1 0 1 1
2 1 1 0
1 1 2 1
B
−
=
. Очевидно, для нее
можно построить четыре различных определителя 3-го порядка. Рассмот-
рим определитель, образованный элементами 2-го, 3-го и 4-го столбцов
матрицы
B
, и вычислим его:
0 1 1 0 0 1
1 1
1 1 0 = 1 1 0 2 0
1 3
1 2 1 1 3 1
−
= = ≠
.
Здесь использовали свойства определителей:
1. Оставили неизменными 1-ый и 3-ий столбцы, а к элементам 2-го
столбца прибавили соответствующие элементы 3-го столбца. Заметили,
почему так поступили? Верно, чтобы получить еще один ноль в 1-ой стро-
ке;
2. Разложили определитель по элементам 1-ой строки.
Для матрицы
B
нашли отличный от нуля определитель 3-го порядка,
следовательно, ранг матрицы
B
равен 3, т.е.
(
)
3
r B
=
.
Поскольку ранги матриц
A
и
B
не равны,
(
)
(
)
r A r B
≠
, то заданная сис-
тема линейных уравнений не имеет решения, т.е. она не совместна.
П р и м е ч а н и е . Количество определителей различного порядка,
порождаемых матрицей, обычно очень велико. Поэтому вычисление ранга
матрицы, основанное непосредственно на вычислении этих определите-
лей, как правило, затруднительно. Существуют особые приемы, значи-
тельно облегчающие задачу нахождения ранга матрицы.
Рассмотрим элементарные преобразования над матрицей, кото-
рые приводят исходную матрицу к эквивалентной матрице:
1. Все строки можно заменить столбцами, т.е. транспонировать мат-
рицу;
2. Можно поменять местами любые две строки (столбца);
3. Можно умножить каждый элемент некоторой строки (столбца) на
один и тот же множитель, отличный от нуля;
4. К элементам любой строки (столбца) можно прибавить соответст-
вующие элементы другой строки (столбца), умноженные на один и тот же
множитель, отличный от нуля.
69
Теорема
(без доказательства).
Элементарные преобразования над матрицей ранга матрицы не ме-
няют
.
Пример 47
. Найдите ранги матриц
A
и
B
, используя элементарные
преобразования и теорему о равенстве рангов эквивалентных матриц.
Решение
Ранг матрицы
A
.
1 0 1 1 0 0 1 0 0 1 0 0 1 0 0
2 1 1 2 1 3 2 1 1 2 1 0 0 1 0
1 1 2 1 1 3 1 1 1 1 1 0 0 1 0
A
−
=
1 0 0
0 1 0
0 0 0
.
Алгоритм элементарных преобразований матрицы
A
1
К элементам 3-го столбца прибавим соответствующие элементы 1-
го столбца;
2
Умножим элементы 3-го столбца на коэффициент
1
3
.
3
От элементов 3-го столбца вычтем соответствующие элементы 2-
го столбца;
4
К элементам 2-ой строки прибавим соответствующие элементы 1-
ой строки, умноженные на коэффициент -2, и от элементов 3-ей строки
вычтем соответствующие элементы 1-ой строки;
5
От элементов 3-го строки вычтем соответствующие элементы 2-ой
строки.
В результате элементарных преобразований над матрицей пришли к
другой матрице (эквивалентной исходной), на главной диагонали которой
стоят единицы, их две. Ясно, что ранг новой матрицы равен двум, следо-
вательно, ранг матрицы системы тоже равен двум:
(
)
2
r A
=
.
Очевидно, что ранг матрицы становится равным количеству еди-
ниц, располагающихся на главной диагонали. Цель элементарных преоб-
разования над матрицей – это стремление получить новую матрицу, экви-
валентную исходной, но в которой элементами являются единицы и нули,
причем строки и столбцы переставляем так, чтобы единицы располага-
лись на главной диагонали.
70
Ранг матрицы
B
.
Описывать последовательность действий не будем. Проследите шаг за
шагом за всеми элементарными преобразованиями матрицы
B
и объясни-
те их.
1 0 1 1 0 0 0 1 0 0 0 1 0 0 0 1
2 1 1 0 2 1 1 0 2 1 1 0 1 1 1 0
1 1 2 1 0 1 3 1 0 1 3 0 0 1 3 0
B
−
=
0 0 0 1 0 0 0 1 0 0 0 1 1 0 0 0
1 1 1 0 1 0 0 0 1 0 0 0 0 1 0 0
0 1 3 0 0 1 3 0 0 1 0 0 0 0 1 0
.
Пришли к эквивалентной матрице, ранг которой равен трем, следова-
тельно,
(
)
3
r B
=
.
Ответ
:
(
)
2
r A
=
,
(
)
3
r B
=
.
10. ТЕСТОВЫЕ ЗАДАНИЯ
Ниже предложены тестовые задания различных типов: задания откры-
того типа, требующие точного лаконичного ответа, задания закрытого ти-
па, где правильный ответ (ответы) выбирается из списка, и задания «на
соответствие» и «на упорядочение», которые, несмотря на простоту по-
ставленного вопроса, требуют хороших навыков решения типовых задач.
Область определения функции
1. Определите, имеет ли функция
8
12
2
−
+
=
x
x
xf )(
вертикальные асим-
птоты?
да;
нет;
имеет асимптоту
1
2
x
= −
.
2.
Укажите все точки разрыва функции
2
5
( )
16
x
f x
x
+
=
−
4
=
x
;
4
−
=
x
;
16
=
x
.
3. Найдите область определения функции
)ln()( 4
2
−= xxf
.

71
)
;
(
)
;
(
+∞
∪
−
−∞
2
2
;
( 2; 2)
−
;
( ; 2) ( 2;2) (2; )
−∞ − ∪ − ∪ +∞
;
)
;
(
+∞
−∞
.
4. Найдите область определения функции
x
xxf
1
4
2
++= )ln()(
.
)
;
(
)
;
(
+∞
∪
−∞
0
0
;
)
;
(
+∞
0
;
)
;
(
+∞
−∞
.
5. Найдите область определения функции
4
42
2
−
+
=
x
x
xf )(
.
)
;
(
)
;
(
+∞
∪
−
−∞
2
2
;
)
;
(
+∞
−∞
;
)
;
(
+∞
−
2
.
6. Найдите область определения функции )
)(log)( 2
2
−
=
xxf
.
)
;
(
+∞
−∞
;
)
;
[
+∞
2
;
)
;
(
+∞
2
.
7. Найдите область определения функции
2
1
2
1
+
+
−
=
x
x
xf )(
.
)
;
(
)
;
(
+∞
∪
−
−∞
2
2
;
( ; 2) ( 2; 2) (2; )
−∞ − ∪ − ∪ +∞
;
( 2; 2)
−
.
8. Найдите область определения функции
4
2
−= xxf )(
.
)
;
(
)
;
(
+∞
∪
−
−∞
2
2
;
)
;
[
]
;
(
+∞
∪
−
−∞
2
2
;
)
;
[
+∞
2
.
9. Найдите область определения функции
x
x
x
f
3
cos
)
(
=
.
)
;
(
+∞
−∞
;
)
;
(
)
;
(
+∞
∪
−∞
0
0
;
)
;
(
π
2
0
.
10. Найдите область определения функции
2
1
2
−
+−=
x
xxf )ln()(
.
)
;
(
+∞
2
;
)
;
[
+∞
2
;
)
;
(
)
;
(
+∞
∪
−
−∞
2
2
;
)
;
(
)
;
(
+∞
∪
−∞
2
2
.
11. Найдите область определения функции
x
e
x
xf
4
2
−
=)(
.
)
;
(
)
;
(
+∞
∪
−
−∞
2
2
;
( 2; 2)
−
;
)
;
(
+∞
−∞
.
12. Найдите область определения функции
2
1
+
=
x
x
xf )(
.
)
;
(
)
;
(
+∞
∪
−
0
0
2
;
)
;
(
)
;
(
+∞
∪
−∞
0
0
;
)
;
(
+∞
−
2
.
13. Найдите область определения функции
x
x
xf ln)( +
−
=
2
1
1
.

72
)
;
(
+∞
1
;
)
;
(
)
;
(
+∞
∪
1
1
0
;
1
≠
x
.
14. Укажите
,
при каких значениях переменной
x
пересекаются линии
2 2
y x
= −
и
2
5 4
y x x
= − +
?
1
=
x
;
2
=
x
;
1
−
=
x
.
15. Область определения функции
1
3
y
x
=
−
задана неравенством:
3
≠
x
;
3
<
x
;
3
≥
x
;
3
≤
x
.
16.
Функция
7)(
24
−−= xxxf
является:
четной;
периодической;
общего вида.
17.
Укажите, имеет ли функция
2
13
4
x
x
x
y
+
+
=
точки разрыва?
Да, это корни уравнения
0
2
4
=
+
x
x
:
3
0, 2
x x
= = −
;
Да, это корни уравнения
3 1 0
x
+ =
;
Функция не имеет точек разрыва;
Функция непрерывна на всей вещественной оси.
18. Укажите вертикальную асимптоту графика функции
3
4
x
y
x
−
=
+
.
3
=
x
;
4
=
x
;
4
−
=
x
.
19. Отметьте все верные высказывания для функции
65
2
−+= xxy
.
Четная;
Вогнутая;
Убывающая;
Имеет экстремум.
20. Укажите область определения функции
1
)(
−
=
x
e
x
xf
.
(1; )
x
∈ +∞
;
( ;1) (1; )
x
∈ −∞ ∪ +∞
;
( ; ).
x
∈ −∞ ∞
21.
Найдите область определения функции
)ln()( xxxf 2
2
+=
.
)
;
(
+∞
0
;
)
;
(
)
;
(
+∞
∪
−
−∞
0
2
;
)
;
(
0
2
−
;
)
;
(
+∞
−∞
.
22. Найдите область определения функции
x
exxf
−
+=
2
2)()(
.
( 2; 2)
−
;
)
;
(
+∞
−∞
;
)
;
(
)
;
(
+∞
∪
−∞
0
0
.
23. Найдите область определения функции
x
xxf
2
2
2
+−= )()(
.
)
;
(
+∞
0
;
)
;
(
)
;
(
+∞
∪
−∞
0
0
;
)
;
(
+∞
2
;
)
;
(
)
;
(
+∞
∪
2
2
0
.
