Суляндзига Е.П., Ушакова Г.А. Тесты по математике: Предел, производная, элементы алгебры и геометрии
Подождите немного. Документ загружается.


13
( )
(
)
3 2
3
2 2
3 3
2 2
5
lim lim
5 5
5 5
lim lim 0.
5 5
x x
x x
x x x
x
x
x x
x x x x
x x
→∞ →∞
→∞ →∞
− −
− = ∞ − ∞ = =
− −
− + ∞
= = = =
∞
− −
Ответ
:
3
2
lim 0.
5
x
x
x
x
→∞
− =
−
Пример 7
. Найти
3
1
1 3
lim
1
1
x
x
x
→
−
−
−
.
Решение
Исследуем выражение, стоящее в скобках. Видно, что при
1
x
→
в зна-
менателях стоят бесконечно малые величины. Поскольку величины, об-
ратные бесконечно малым, являются бесконечно большими, то имеем
разность двух бесконечно больших величин, а это есть неопределенность.
Заметим, что знаменатель второй дроби есть разность кубов. Вос-
пользуемся формулой сокращенного умножения и разложим разность ку-
бов на произведение двух множителей
( )
(
)
3 2
1 1 1
x x x x
− = − + +
.
Итак, имеем
( )
( )
( )
( )
( )
( )
( )
( )
( )
3
2
1 1
2
2 2
1
2
2
1
1 3 1 3
lim lim
1 1
1
1 1
1 3
lim
1 1 1 1
2 0
lim .
0
1 1
x x
x
x
x x
x
x x x
x x
x x x x x x
x x
x x x
→ →
→
→
− = ∞ − ∞ = − =
− −
−
− + +
+ +
= − =
− + + − + +
− + +
=
− + +
Как видно, пришли к неопределенности
0
.
0
Со знаменателем все ясно. Но многочлен второй степени
( ) ( )
2
2
2
f x x x P x
= − + + =
, стоящий в числителе, при
1
x
=
обращается в
ноль, т. е.
(
)
1 0.
f
=
А это значит,
1
x
=
является корнем уравнения
( )
2
2 0
f x x x
= − + + =
. Решите это уравнение и найдете два корня. Один
уже известен, это
1
x
=
, другой же
2
x
=
. Таким образом, многочлен второй

14
степени (или квадратный трехчлен)
( )
2
2
2
P x x x
= − + +
можно представить
в виде произведения двух линейных множителей, а именно:
( )( )
2
2 1 2 .
x x x x− + + = − −
Используем полученное разложение и продолжим решение поставлен-
ной задачи.
( )
( )
(
)
(
)
( )
( )
( )( )
( )
( )
( )
( )
2
2 2
1 1
2 2
1 1
1 2
2
lim lim
1 1 1 1
1 2 2
1
lim lim
3
1 1 1
x x
x x
x x
x x
x x x x x x
x x x
x x x x x
→ →
→ →
− −
− + +
= =
− + + − + +
− − −
= − = − =
− + + + +
Здесь вынесли знак минус:
(
)
1 1
x x
− = − −
и сократили бесконечно ма-
лые величины
(
)
1
x
−
при
1
x
→
. Дальнейшая подстановка
1
x
=
в остав-
шееся выражение дает окончательный результат.
( )
( )
2
2
1
2 1
lim .
3
1 1
x
x x
x x x
→
− + +
=
− + +
А это значит, что
3
1
1 3 1
lim .
1 3
1
x
x
x
→
− =
−
−
Ответ
:
3
1
1 3 1
lim .
1 3
1
x
x
x
→
− =
−
−
Анализируя методы раскрытия неопределенности вида
(
)
∞ − ∞
,
можно отметить, что, как правило, неопределенность вида
(
)
∞ − ∞
, сво-
дится к неопределенностям вида
∞
∞
или
0
.
0
Первый замечательный предел
0
lim 1
x
sinx
x
→
=
Рассматривая отношение
sinx
и
x
при стремлении аргумента
x
к нулю,
имеем отношение двух бесконечно малых величин. А это есть неопреде-
ленность вида
0
0
.
Доказательство
0
0
lim 1
0
x
sinx
x
→
= =
строится на геометрическом пред-
ставлении функций
,
sin x tg x
в окружности единичного радиуса и теоре-
мы о том, что центральный угол измеряется дугой, на которую он опирает-
ся. Сравнивая
, ,
sin x x tg x
, приходим к двойному неравенству
sin x x tg x
Ј Ј
. Дальнейшие очевидные преобразования и переход к пре-

15
делу при стремлении аргумента
x
к нулю, а также использование теоремы
о пределах трех монотонных функций
3
приводят к доказательству того,
что
0
lim 1
x
x
sinx
→
=
. Отсюда следует, что
0
lim 1
x
sinx
x
→
=
.
Основным достоинством этого предела, почему он и называется заме-
чательным, является эквивалентность двух бесконечно малых величин
sin x
и его аргумента
x
:
sin x
∼
x
. Отсюда получаем и другие эквива-
лентные функции при
0
x
→
, а именно,
, , .
tgx x arcsinx x arctgx x
: : :
Пусть
(
)
lim 0,
x a
x
α
→
=
т.е.
(
)
x
α
бесконечно малая при
.
x a
→
Можно полу-
чить еще несколько пар эквивалентных функций, которые для студентов
технических специальностей значительно упрощают вычисления.
Пример 8
. Найти
0
3
lim
x
sin x
x
→
.
Решение
Заметим, что
0
3 0
lim
0
x
sin x
x
→
=
. Поскольку
0
x
→
воспользуемся эквива-
лентными бесконечно малыми величинами
3 3
sin x x
:
, будем иметь
0 0
3 0 3
lim lim 3
0
x x
sin x x
x x
→ →
= = =
.
Ответ
:
0
3
lim 3.
x
sin x
x
→
=
3
Пусть функции
( ) ( ) ( )
, ,
s x f x g x
на некотором множестве
X
монотонно убывают, причем
для
x X
О
( ) ( ) ( )
s x f x g x
Ј Ј
. Тогда если
( )
lim ,
s x A
x a
=
®
и
( )
lim
g x A
x a
=
®
, то
( )
lim
f x A
x a
=
®
.
(
)
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( )
( ) ( )
( )
( )
( )
( )
lim 0
, ,
, ,
1 , ,
1 .
x a
x
x
x
sin x x tg x x
arcsin x x arctg x x
e x ln 1+ x x
a x
α
α
α
α α α α
α α α α
α α α
α
→
=
−
−
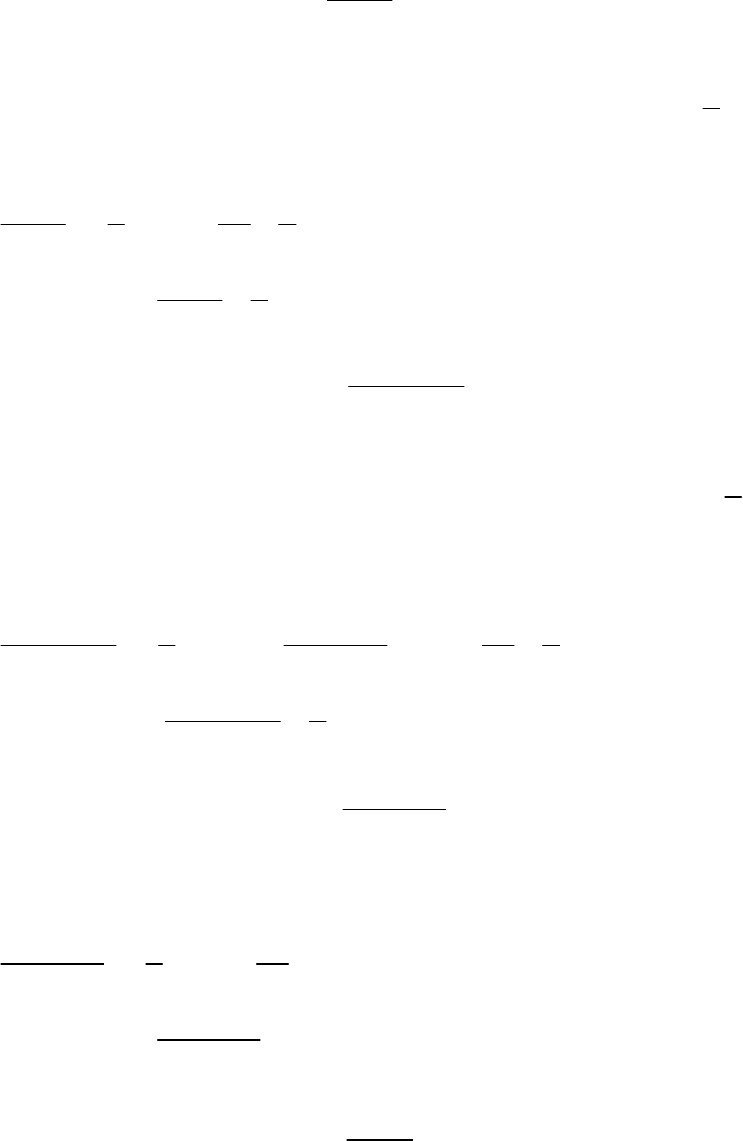
16
Пример 9
. Найти
0
7
lim
5
x
tg x
sin x
→
.
Решение
При
0
x
→
в пределе имеем неопределенность вида
0
0
. Используя эк-
вивалентные бесконечно малые величины
7 7 , 5 5 ,
tg x x sin x x
: :
получим
0 0
7 0 7 7
lim lim .
5 0 5 5
x x
tg x x
sin x x
→ →
= = =
Ответ
:
0
7 7
lim .
5 5
x
tg x
sin x
→
=
Пример 10
. Найти
0
3 4
lim
9
x
arcsin x
tg x
→
.
Решение
При
0
x
→
в пределе имеем неопределенность вида
0
0
. Используем
при
0
x
→
эквивалентные бесконечно малые величины:
4 4 , 9 9
arcsin x x tg x x
: :
. Решение записываем как
0 0 0
3 4 0 4 4 4
lim 3 lim 3 lim .
9 0 9 9 3
x x x
arcsin x arcsin x x
tg x tg x x
→ → →
= = = =
Ответ
:
0
3 4 4
lim .
9 3
x
arcsin x
tg x
→
=
Пример 11
. Найти
0
4
lim
2
x
arcsin x
arctg x
→
.
Решение
Хочется верить, что решение данного примера очевидно, а именно:
0 0
4 0 4
lim lim 2.
2 0 2
x x
arcsin x x
arctg x x
→ →
= = =
Ответ
:
0
4
lim 2.
2
x
arcsin x
arctg x
→
=
Пример 12
. Найти
3
lim
2
x
sin x
sin x
π
→
.
Решение
Сразу отметим, что в этом примере надо будет обязательно сделать
переход к новой переменной, стремящейся к нулю, для того, чтобы вос-
пользоваться эквивалентными бесконечно малыми величинами.
Если проанализировать выражение, стоящее за знаком предела, то
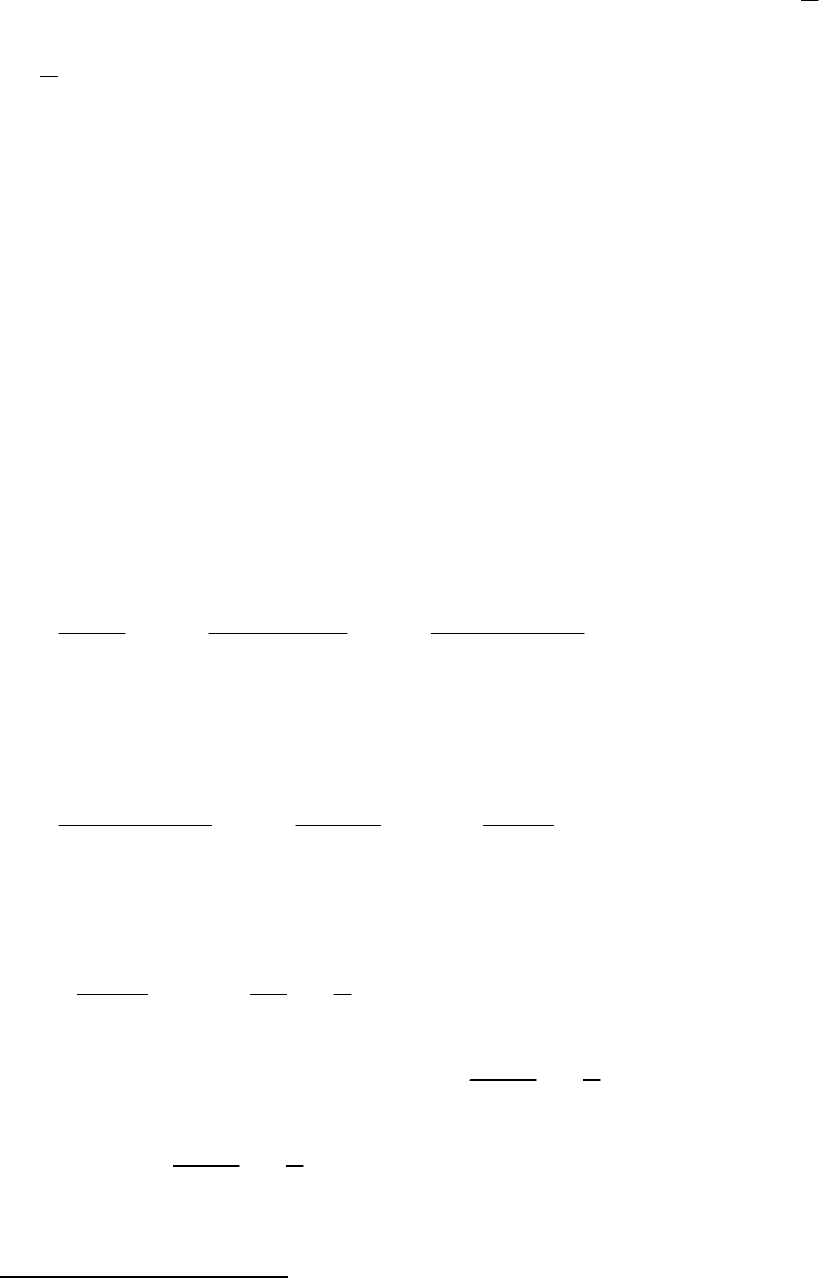
17
можно увидеть, что при
x
π
→
имеем неопределенность вида
0
0
. Однако
ответ
3
2
будет неверным.
Понятно, что есть желание объявить эквивалентными функции
3
sin x
и
3
x
,
2
sin x
и
2
x
. Но это неверно, потому что
x
π
→
, а
π
не есть ноль, это од-
на из известных констант
4
:
3,14
π
≈
. Вы предлагаете заменить бесконечно
малые величины
3
sin x
и
2
sin x
при
x
π
→
величинами
3 3 3,14 9,42
π
≈ ⋅ =
и
2 2 3,14 2,28
π
≈ ⋅ =
соответственно. Теперь видно, что это неверно! Так ка-
кой выход существует из этой ситуации?
Рассудим следующим образом: если
x
π
→
, то разность
x
π
−
или
x
π
−
есть бесконечно малая величина. Рассмотрим бесконечно малую ве-
личину
x
π
−
, обозначим ее
α
, т. е.
x
α π
= −
. Теперь если
x
π
→
, то оче-
видно:
0
α
→
. Выразим
x
из предложенного равенства:
x
π α
= +
. Подста-
вим полученное выражение для переменной
x
через переменную
α
в ис-
ходное, стоящее под знаком предела, и перейдем к пределу при условии,
что
0.
α
→
Будем иметь
(
)
( )
(
)
( )
0 0
3 3 3
3
lim lim lim .
2 2 2 2
x
sin sin
sin x
sin x sin sin
π α α
π α π α
π α π α
→ → →
+ +
= =
+ +
Воспользуемся формулами приведения:
(
)
3 3 3
sin sin
π α α
+ = −
,
(
)
2 2 2
sin sin
π α α
+ =
и продолжим решение:
(
)
( )
0 0 0
3 3
3 3
lim lim lim .
2 2 2 2
sin
sin sin
sin sin sin
α α α
π α
α α
π α α α
→ → →
+
−
= = −
+
И только теперь имеем полное право использовать эквивалентные бес-
конечно малые величины:
3 3
sin
a a
:
,
2 2
sin
a a
:
. Продолжим решение:
0 0
3 3 3
lim lim .
2 2 2
sin
sin
α α
α α
α α
→ →
− = − = −
Таким образом, получили, что
3 3
lim .
2 2
x
sin x
sin x
π
→
= −
Ответ
:
3 3
lim .
2 2
x
sin x
sin x
π
→
= −
4
Число π можно получить, если длину окружности разделить на длину диаметра. Получим число,
которое нельзя представить ни конечной десятичной дробью, ни периодической дробью. Приближенное
значение числа π с шестнадцатью значащими цифрами:π=3,141592653589793.
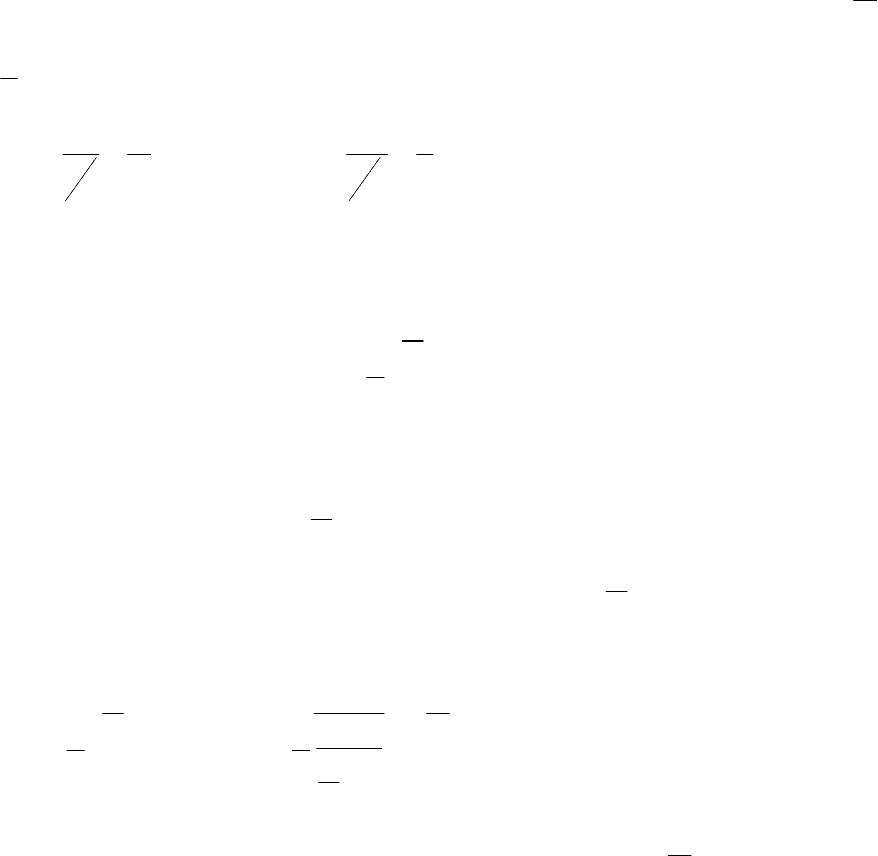
18
Правило раскрытия неопределенности вида
0
⋅∞
Прежде, чем раскрывать неопределенность вида
(
)
0
⋅∞
, отметим, что
такую неопределенность может дать произведение двух множителей, один
из которых есть бесконечно малая величина, а другой
−
бесконечно боль-
шая. Избавиться от такой неопределенности можно, если один из множи-
телей опустить в знаменатель, при этом выполнив правильно эквивалент-
ные преобразования. И тогда придем к неопределенности либо
∞
∞
, либо
0
0
, правила раскрытия которых уже известны. В самом деле,
0
1
0
∞ ∞
⋅∞ = =
∞
или
0 0
0
1
0
⋅∞ = =
∞
. На вопрос, какой множитель убрать в
знаменатель, можно ответить только после анализа функции, предел ко-
торой находим. Главная цель – решение должно быть простым и краси-
вым.
Пример 13
. Найти
2
lim
2
x
x tgx
π
π
→
− ⋅
.
Решение
Анализируя стоящее за знаком предела выражение, приходим к выво-
ду, что при условии
2
x
π
→
имеем неопределенность вида
0
⋅∞
. Выполним
эквивалентные преобразования выражения
2
x tgx
π
− ⋅
. Перенесем пер-
вый множитель заданного выражения в знаменатель:
2 2
lim lim .
1
2
2
x x
tgx
x tgx
x
π π
π
π
→ →
∞
− ⋅ = =
∞
−
Как видно, пришли к неопределенности вида
∞
∞
, но выхода из соз-
давшейся ситуации не видно.
П р и м е ч а н и е . Эту неопределенность можно раскрыть. С помощью
правила Лопиталя. Причем только после третьего раза применения, но при
этом надо будет полученные выражения упрощать. Проверьте, так ли это.
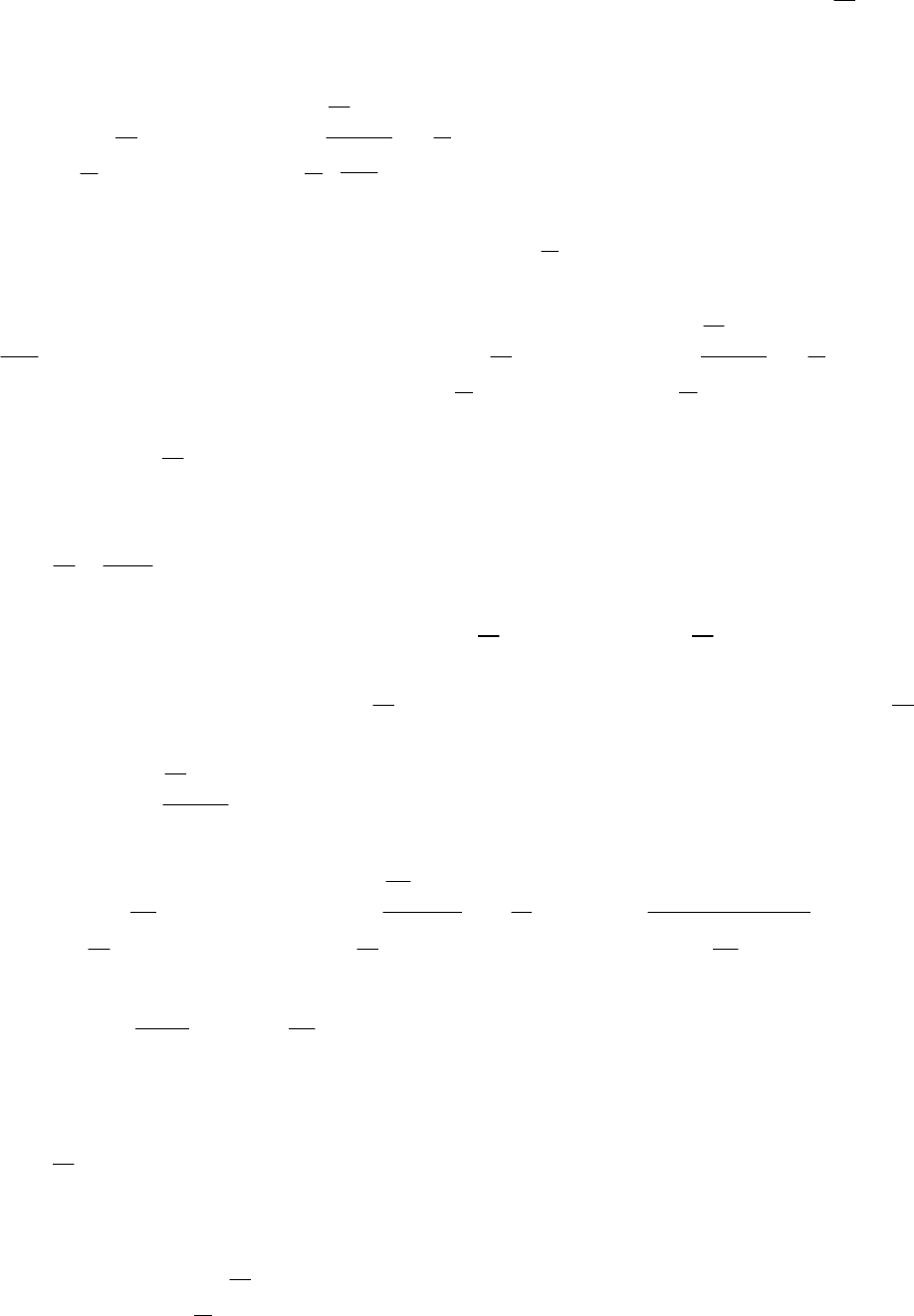
19
Поступим иначе, перенесем второй множитель выражения
2
x tgx
π
− ⋅
в
знаменатель:
2 2
0
2
lim lim .
1
2 0
x x
x
x tgx
tgx
π π
π
π
→ →
−
− ⋅ = =
Получили неопределенность вида
0
0
, и более того известно, что
1
ctgx
tgx
=
. Итак, будем иметь
2 2
0
2
lim lim .
2 0
x x
x
x tgx
ctgx
π π
π
π
→ →
−
− ⋅ = =
Заметим,
что при
2
x
π
→
0
ctgx
→
, но здесь нельзя сказать об эквивалентности бес-
конечно малой функции
ctgx
и ее аргумента
x
, поскольку
3,14
1,57.
2 2
x
π
→ = =
Как и в предыдущем примере выполним преобразова-
ния: введем новую переменную
2
x
π
α
= −
. Если
2
x
π
→
, то
0
α
→
. Выразим
переменную
x
через
α
:
2
x
π
α
= −
, подставим найденный
x
и
2
x
π
α
= −
в
выражение
2
x
ctgx
π
−
и продолжим нахождение заданного предела:
0
2 2
0 0
0
2
lim lim lim
2 0
2
lim lim 1.
x x
x
x tgx
ctgx
ctg
tg
π π
α
α α
π
π α
π
α
α α
α α
→
→ →
→ →
−
− ⋅ = = = =
−
= = =
В данных преобразованиях применили формулу приведения
2
ctg tg
π
α α
− =
и эквивалентные бесконечно малые величины
tg
α
и
α
при условии, что
0 :
α
→
.
tg
α α
Ответ
:
2
lim 1.
2
x
x tgx
π
π
→
− ⋅ =
20
Второй замечательный предел
( )
1
0
lim 1
x
x
x e
®
+ =
или
1
lim 1
x
x
e
x
® Ґ
ж ц
ч
з
+ =
ч
з
ч
з
и ш
Прежде надо отметить, что здесь имеем неопределенность вида
(
)
1
∞
.
Действительно,
(
)
0
lim 1 1
x
x
®
+ =
и
1
lim 1 1.
x
x
® Ґ
ж ц
ч
з
+ =
ч
з
ч
з
и ш
Кто-то скажет, что если еди-
ницу возвести в любую степень, то получим только единицу. Откуда же
берется константа
e
? Дело в том, что в степень возводим не чистую еди-
ницу, а величину, близкую к единице. Вот этот «хвост» с единицей, возве-
денные в степень, и дают в пределе константу
e
. Кроме того заметим,
что в показателе стоит величина, обратная той бесконечно малой величи-
не, которая добавляется к единице, находящейся в основании. Константа
e
есть иррациональное
5
число.
Если взять два соседних целых числа
n
,
1
n
+
и число
x
, находящееся
между ними, т. е. удовлетворяющее неравенствам
1
n x n
≤ ≤ +
, то можно
проделать такие несложные выкладки, проследите за ними.
1
1 1 1 1 1 1 1 1 1
; 1+ 1 1 ; 1+ 1 1 ;
1 1 1
1 1 1
1+ 1 1 , здесь 1 .
1
n x n
n x n n x n n x n
n x n
n x n
+
≥ ≥ ≥ + ≥ + ≥ + ≥ +
+ + +
≥ + ≥ + + ≥ ≥
+
Для наглядности рассуждений перепишем последнее выражение,
изменив порядок следования величин от меньшей к большей:
1
1 1 1
1 1 1+
1
n x n
n x n
+
+ ≤ + ≤
+
.
Рассмотрим
1
1
1
n
n
+
ж ц
ч
з
+
ч
з
ч
з
и ш
, заметим, что самое большое значение это вы-
ражение будет иметь когда
1
n
=
, в самом деле, при
1
n
=
1
1
1 4
n
n
+
ж ц
ч
з
+ =
ч
з
ч
з
и ш
.
Выражение
1
1
1
n
n
+
+
принимает самое большое значение тоже при
1
n
=
,
5
Рациональное число – это целое или дробное, представленное конечной десятичной или перио-
дической дробью. Иррациональное число – это число, которое не является рациональным. Иррацио-
нальное число записывается бесконечной непериодической десятичной дробью. Иррациональное число
e с шестнадцатью значащими цифрами запишется как е = 2,718281828459045.

21
это будет
1 3
1 1,5
1 2
n
n
+ = =
+
. Следовательно, значения выражения
1
1
x
x
+
находятся на отрезке [1,5; 4]. Это достаточно грубая оценка. Бо-
лее изящные исследования дают результат
1
2 1 3
1
n
n
< + <
+
. Вычисления
1
1
1
n
n
+
+
при разных значениях
n
на современных персональных компью-
терах позволяют убедиться, что
1
lim 1
1
n
n
e
n
→∞
+ =
+
. Полагая
[ ; 1]
x n n
∈ +
,
легко получить
1
lim 1
x
x
e
x
® Ґ
ж ц
ч
з
+ =
ч
з
ч
з
и ш
.
Этот предел можно записать иначе, если устремить переменную
x
к
нулю, а именно,
( )
1
0
lim 1
x
x
x e
®
+ =
.
Рассмотрим несколько примеров на нахождение предела, решение
которых можно получить с помощью второго замечательного предела.
П р и м е ч а н и е . Если выражение, стоящее за знаком предела дает
неопределенность вида
(
)
1
∞
, то задачу нахождения предела надо сводить
ко второму замечательному пределу, в противном случае результат оче-
виден.
Пример 14
. Найти
3
5 1
lim
2
x
x
x
x
→∞
+
+
.
Решение
Сначала рассмотрим выражение, записанное в круглых скобках, и най-
дем предел его при указанном стремлении переменной
x
к
∞
, т. е.
5 1
lim 5
2
x
x
x
→∞
+ ∞
= =
+ ∞
.
Теперь можем сказать, что
3
5 1
lim 5 .
2
x
x
x
x
∞
→∞
+
= = ∞
+
Ответ
:
3
5 1
lim .
2
x
x
x
x
→∞
+
= ∞
+

22
Пример 15
. Найти
1
3 1
lim
7 2
x
x
x
x
+
→∞
+
−
.
Решение
Сначала найдем
3 1
lim
7 2
x
x
x
→∞
+
−
. Будем иметь
3 1 3
lim
7 2 7
x
x
x
→∞
+ ∞
= =
− ∞
. Теперь
ответ очевиден:
1
3 1 3
lim 0
7 2 7
x
x
x
x
+ ∞
→∞
+
= =
−
.
Ответ
:
1
3 1
lim 0
7 2
x
x
x
x
+
→∞
+
=
−
.
Пример 16
. Найти
2
1
lim
3
x
x
x
x
→∞
+
−
.
Решение
Найдем
1
lim
3
x
x
x
→∞
+
−
. Получим
1
lim 1
3
x
x
x
→∞
+ ∞
= =
− ∞
.
Теперь преобразуем дробь
1
3
x
x
+
−
так, чтобы единица была явно выде-
лена. Это можно сделать, по крайней мере, тремя способами. Рассмотрим
из них два простейших
6
.
Первый способ
Прибавим к дроби единицу, затем ее вычтем, и приведем два послед-
них слагаемых к общему знаменателю:
(
)
1 3
1 1 4
1 1 1 1
3 3 3 3
x x
x x
x x x x
+ − −
+ +
= + − = + = +
− − − −
.
Второй способ
В числителе отнимем и добавим нужную константу, а затем разобьем
полученную дробь на две дроби, одна из которых дает единицу:
(
)
3 4
1 3 3 1 4
1
3 3 3 3
x
x x
x x x x
− +
+ − + +
= = = +
− − − −
.
Как видно, результат получили один и тот же. Исследуя выражение
6
На жаргонном языке такой метод можно назвать методом Тараса Бульбы: “я тебя породил, я тебя
и убью”. Этот метод очень удобен при выделении полного квадрата. Например,
( )
2
2 2 2
6 1 2 3 1 2 3 9 9 1 3 8
x x x x x x x
− + = − ⋅ + = − ⋅ + − + = − −
