Суляндзига Е.П., Ушакова Г.А. Тесты по математике: Предел, производная, элементы алгебры и геометрии
Подождите немного. Документ загружается.

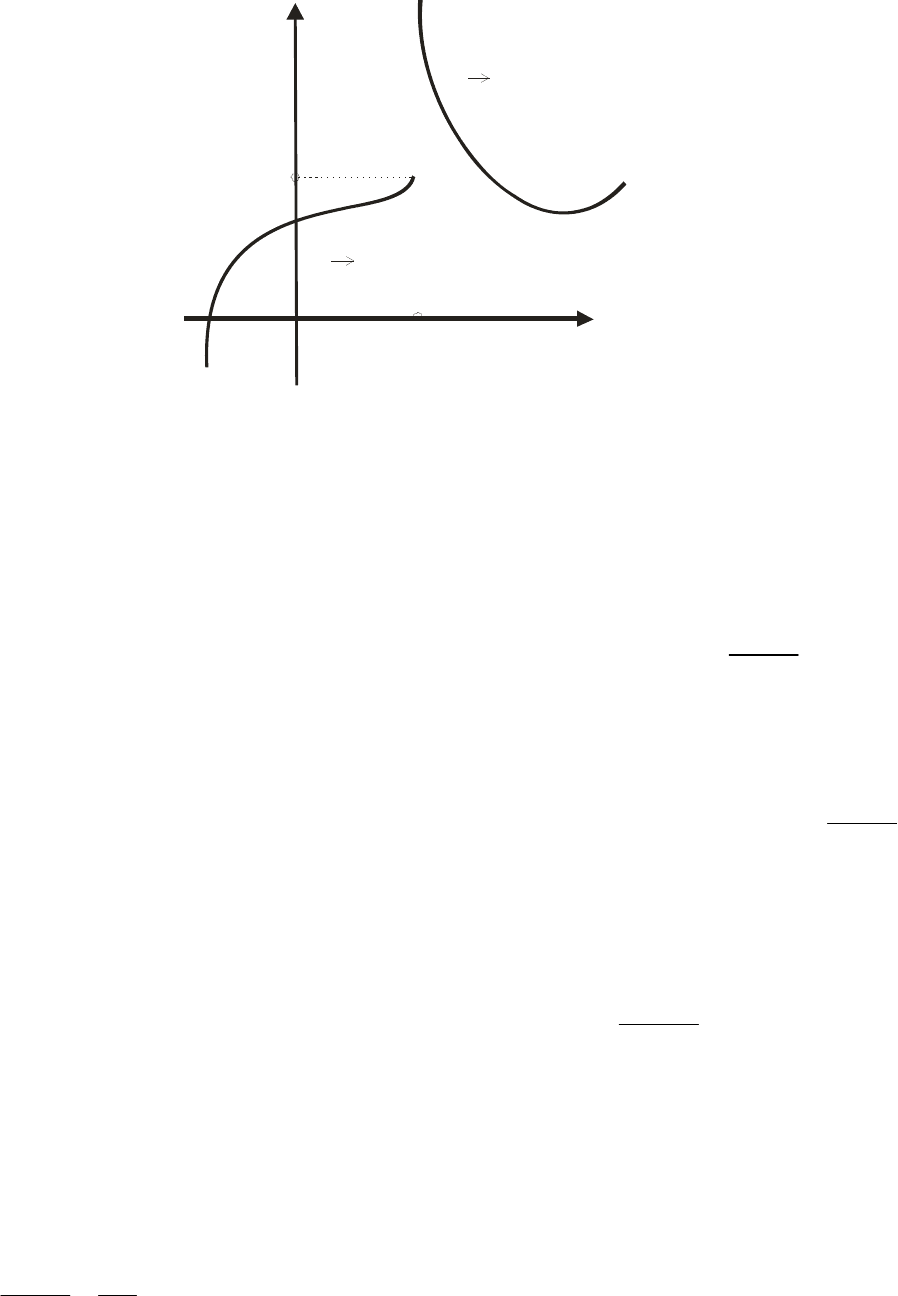
43
x
y
a
b
a -
2
точка разрыва
-го рода
lim f(x) = b
lim f(x) =
x a - 0
x a + 0
8
Рис. 3. Разрыв функции 2-го рода:
(
)
0
lim
x a
f x b
→ −
=
,
(
)
0
lim
x a
f x
→ +
= ∞
Все элементарные функции непрерывны в своих областях опреде-
ления.
Пример 37.
Установите, является ли функции
3 5
2
x
y
x
+
=
−
непре-
рывной. Если нарушается непрерывность функции, то укажите точки и вид
разрыва.
Решение
В примере 36 показали, что область определения функции
3 5
2
x
y
x
+
=
−
есть вся вещественная ось, кроме точки
2
x
=
. Исследуем поведение за-
данной функции в окрестности точки
2
x
=
. Для этого найдем односторон-
ние пределы функции при условии, что
x
стремится к 2 слева, а именно,
2 0
x
→ −
, и
x
стремится к 2 справа, т.е.
2 0
x
→ +
.
Вычислим левосторонний предел функции
2 0
3 5
lim
2
x
x
x
→ −
+
−
.
Если аргумент
x
стремится к 2 слева, то это означает, что
x
близок к 2,
но все время меньше, чем 2. Предположим, что
1.99999
x
=
, тогда величина
2
x
α
− = −
является бесконечно малой отрицательной. Предел числителя
3 5
x
+
при условии
2 0
x
→ −
равен 11. В самом деле
2 0
lim 3 5 11
x
x
→ −
+ =
. То-
гда предел заданной функции при
2 0
x
→ −
находим как
2 0
3 5 11
lim
2
x
x
x
α
→ −
+
= = −∞
− −
.

44
Найдем правосторонний предел функции
2 0
3 5
lim
2
x
x
x
→ +
+
−
.
Аргумент
x
стремится к 2 справа. Это значит, что
x
очень близок к 2,
но остается все время большим, чем 2. Допустим,
2.00001
x
=
, тогда вели-
чина
2
x
α
− =
является бесконечно малой положительной величиной, т.е.
0
α
→
. Предел числителя
3 5
x
+
при условии
2 0
x
→ +
тоже равен 11. В
самом деле
2 0
lim 3 5 11
x
x
→ +
+ =
. Тогда предел заданной функции при
2 0
x
→ +
вычисляем как
2 0
3 5 11
lim
2
x
x
x
α
→ +
+
= = ∞
−
.
Таким образом, имеем
2 0 2 0
3 5 3 5
lim , lim
2 2
x x
x x
x x
→ − → +
+ +
= −∞ = +∞
− −
.
Поскольку оба предела есть бесконечно большие величины при
2 0
x
→ ±
, следовательно,
2
x
=
является точкой разрыва 2-го рода.
Ответ
:
2
x
=
является точкой разрыва 2-го рода.
Пример 38.
Установите, является ли функции
(
)
3
y ln x
= +
непре-
рывной. Если нарушается непрерывность, то укажите точки разрыва и на-
зовите вид разрыва.
Решение
В примере 35 показали, что область определения функции
(
)
3
y ln x
= +
есть бесконечный интервал
(
)
3; .
− ∞
Из определения элементарной функ-
ции
(
)
y ln x
=
известно, что
(
)
0
lim
x
f x
→ +
= −∞
. Обратите внимание, здесь
0
x
→ +
. Это говорит о том, что
x
стремится к нулю, оставаясь при этом все
время положительным, т.е.
0
x
→
справа. В нашем же случае аргументом
логарифмической функции является выражение
3
x
+
. Из сказанного сле-
дует, что
3 0
x
+ >
и
3 0
x
+ → +
, а это означает, что
3 0
x
→ − +
. Таким обра-
зом, можно сделать вывод, что
3
x
= −
является точкой разрыва 2-го рода,
так как
(
)
3 0
lim 3
x
ln x
→ − +
+ = −∞
.
Ответ
:
3
x
= −
является точкой разрыва 2-го рода.
Пример 39.
Определите, является ли функции
2
1,
если 1;
1,
если 1
x x
y
x x
+ ≤
=
+ >
непрерывной. Если
нарушается непрерывность, то укажите точки и вид
разрыва.
Решение
Из задания функции видно, что при
1
x
≤
это линейная функция
1
y x
= +
,
45
а при
1
x
>
−
это парабола
2
1
y x
= +
. Эти функции определены при всех
своих значениях аргумента. Неясность вносит
1
x
=
. Найдем односторон-
ние пределы заданной функции при
1
x
→
.
Вычислим левосторонний предел функции при
1
x
→
, т.е. при
1 0
x
→ −
.
Здесь в качестве функции для исследования возьмем
1
y x
= +
. Име-
ем
(
)
1-0
lim 1 2
x
x
→
+ =
.
Найдем правосторонний предел функции при
1
x
→
, т.е. при
1 0
x
→ +
. В
этом случае исследуем поведение функции
2
1
y x
= +
. Таким образом,
(
)
2
1+0
lim 1 2
x
x
→
+ =
.
Из задания функции видно, что
(
)
1 2
f
=
. Вычисления односторонних
пределов дали результат:
( )
(
)
2
1-0 1+0
lim 1 lim 1 2
x x
x x
→ →
+ = + =
.
Вывод
: поскольку односторонние пределы функции при
1
x
→
равны, и
равны они
(
)
1
f
−
значению функции в точке
1
x
=
, т.е.
(
)
1-0
lim 1
x
x
→
+ =
(
)
( )
2
1+0
lim 1 1 2
x
x f
→
= + = =
, то имеем право сказать, что заданная функция
непрерывна на всей вещественной оси, в том числе и при
1
x
=
. Область
определения и область непрерывности заданной функции:
(
)
,R
= −∞ +∞
.
Ответ
: функция непрерывна для всех
(
)
,x
∈ −∞ +∞
.
5. АСИМПТОТЫ
Асимптотой графика функции
(
)
y f x
=
называется прямая, к кото-
рой график функции неограниченно приближается при удалении точки
графика от начала координат.
График функции может иметь асимптоты, но может и не иметь их.
Асимптоты могут быть трех видов.
Вертикальные асимптоты
. Их проще всего определять. Надо
уметь находить точки разрыва второго рода. Уравнение вертикальной
асимптоты записывается
x a
=
, как уравнение прямой, параллельной оси
Oy
. При этом
(
)
a a
lim lim
x x
y f x
→ →
= = ±∞
.
Горизонтальные асимптоты
. Чтобы их найти, надо уметь вычис-
лять
(
)
lim lim
x x
y f x
→ ±∞ → ±∞
=
. Предположим, что
(
)
lim
x
f x b
→ −∞
=
или
46
(
)
+
lim
x
f x b
→ ∞
=
, причем
b
≠ ±∞
. Тогда говорят, что график функции имеет
горизонтальную асимптоту при
x
→ −∞
либо при
x
→ +∞
. В таком случае
горизонтальная асимптота записывается уравнением
y b
=
, как уравнение
прямой, параллельной оси
Ox
.
Наклонные асимптоты
записываются уравнением
y kx b
= +
. Это
уравнение прямой с угловым коэффициентом
k
. Величина
b
−
величина
отрезка, отсекаемого прямой
y kx b
= +
на оси
Oy
. Значения
k
,
b
надо оп-
ределить, исходя из заданной функции, асимптоты которой отыскиваем.
Как найти коэффициенты
k
,
b
уравнения наклонной асимптоты
y kx b
= +
?
Прямые
y kx b
= +
и
y kx
=
параллельны. Прямая
y kx
=
проходит через
начало координат. Из уравнения
y kx
=
находим
y
k
x
=
. Если коэффициент
k
будет найден, то из уравнения
y kx b
= +
определим коэффициент
b
:
b y kx
= −
. Находим наклонные асимптоты графика функции
(
)
y f x
=
. Из
определения асимптоты и полученных выражений для величин
k
,
b
при-
ходим к формулам, позволяющих вычислить коэффициенты
k
,
b
уравне-
ния
y kx b
= +
наклонной асимптоты графика функции
(
)
y f x
=
.
(
)
lim lim
x x
f x
y
k
x x
→±∞ →±∞
= =
;
(
)
(
)
(
)
lim lim
x x
b y kx f x kx
→±∞ →±∞
= − = −
.
П р и м е ч а н и е 1 . Если
(
)
lim 0
x
f x
k
x
→±∞
= =
, то наклонные асимптоты
вырождаются в горизонтальные. В самом деле, уравнение наклонной
асимптоты
y kx b
= +
принимает вид
0
y kx b x b b y b
= + = + = ⇒ =
.
П р и м е ч а н и е 2. Коэффициенты
k
,
b
уравнения
y kx b
= +
на-
клонной асимптоты надо находить при
x
→ −∞
и при
x
→ +∞
отдельно.
Определяем
(
)
lim
x
f x
k
x
→ −∞
=
,
(
)
(
)
lim
x
b f x kx
→ −∞
= −
при
x
→ −∞
. Если эти
пределы существуют, то уравнение наклонной асимптоты записываем как
y kx b
= +
. Асимптоту в этом случае называют
левой
наклонной асимпто-
той. В самом деле,
x
стремится к
−∞
, т.е.
x
→ −∞
.

47
Если коэффициенты
k
,
b
находим при
x
→ +∞
, т.е.
(
)
+
lim
x
f x
k
x
→ ∞
=
и
(
)
(
)
+
lim
x
b f x kx
→ ∞
= −
, и они существуют, то говорим, что получили уравне-
ние
y kx b
= +
правой
наклонной асимптоты.
Пример 40.
Найдите асимптоты графика функции
3 5
2
x
y
x
+
=
−
.
Решение
Решение этого примера состоит из трех этапов: нахождение верти-
кальной асимптоты, горизонтальной асимптоты и наклонной.
Данную функцию рассматривали в примерах 35 и 37. Она не яв-
ляется непрерывной и имеет разрыв второго рода, при этом
2 0 2 0
3 5 3 5
lim , lim
2 2
x x
x x
x x
→ − → +
+ +
= −∞ = +∞
− −
. Следовательно,
2
x
=
−
уравнение
вертикальной асимптоты.
Найдем горизонтальные асимптоты. Для этого надо найти
3 5
lim
2
x
x
x
→ +∞
+
−
и
3 5
lim .
2
x
x
x
→ −∞
+
−
Сначала рассмотрим
3 5
lim
2
x
x
x
→ +∞
+
−
.
3 5 3
lim 3.
2 1
x
x
x
→ +∞
+
= =
−
Следовательно,
3
y
=
−
уравнение горизонтальной
асимптоты при
x
→ +∞
.
Теперь найдем
3 5
lim .
2
x
x
x
→ −∞
+
−
В этом пределе надо учесть, что аргу-
мент
x
все время остается отрицательным. Введем новую положительную
переменную
(
)
0
t t
>
:
x t
= −
, откуда следует, что
t x
= −
. Из этой замены
видно, что при
x
→ −∞
переменная
t
→ ∞
. Воспользуемся новой перемен-
ной
t
, подставим
x t
= −
в искомый предел. Будем иметь
(
)
3 5
3 5 3 5 3
lim lim lim 3.
2 2 2 1
x t t
t
x t
x t t
→ −∞ → ∞ → ∞
− +
+ − + −
= = = =
− − − − − −
Вычисления показали, что значение предела при
x
→ −∞
не измени-
лось. А это означает, что график функции
3 5
2
x
y
x
+
=
−
при
x
→ −∞
прибли-
жается к прямой
3
y
=
, которая называется горизонтальной асимптотой.
48
Таким образом, уравнение
3
y
=
является горизонтальной асимптотой.
Заметим, что замену переменной
x t
= −
, где
0
t
>
, делаем всегда,
когда находим предел функции при
.
x
→ −∞
Имеет ли график заданной функции наклонные асимптоты, урав-
нения которых записываются
y kx b
= +
?
Вычислим сначала угловой коэффициент
k
по формуле
(
)
lim
x
f x
k
x
→±∞
=
.
Рассмотрим случай, когда
.
x
→ +∞
Будем иметь
(
)
lim
x
f x
k
x
→+∞
= =
( )
3 5 3 5
lim : lim 0.
2 2
x x
x x
x
x x x
→+∞ →+∞
+ + ∞
= = = =
− − ∞
Отсюда следует, что
0
k
=
.
Очевидно, что при
x
→ −∞
получим то же самое значение предела.
Поскольку
0
k
=
, то можно сделать вывод, что график заданной функ-
ции не имеет наклонных асимптот.
Ответ
: заданная функция
3 5
2
x
y
x
+
=
−
имеет вертикальную асимптоту
2
x
=
и горизонтальную асимптоту
3
y
=
. Наклонных асимптот нет.
6. ПРЯМАЯ НА ПЛОСКОСТИ
Рассмотрим три способа задания прямой на плоскости. Прежде всего
отметим, что это линейные уравнения, т.е. такие уравнения, в которых пе-
ременные
x
и
y
содержатся только в первых степенях.
Уравнение прямой с угловым коэффициентом
y kx b
= +
.
Сначала исследуем прямую, которая задана уравнением
y kx
=
. Эта
прямая всегда проходит через начало координат, т.е. через точку
(
)
0;0 .
O
Коэффициент
k
называется угловым коэффициентом. Равен он тангенсу
угла наклона, образуемого прямой с положительным направлением оси
Ox
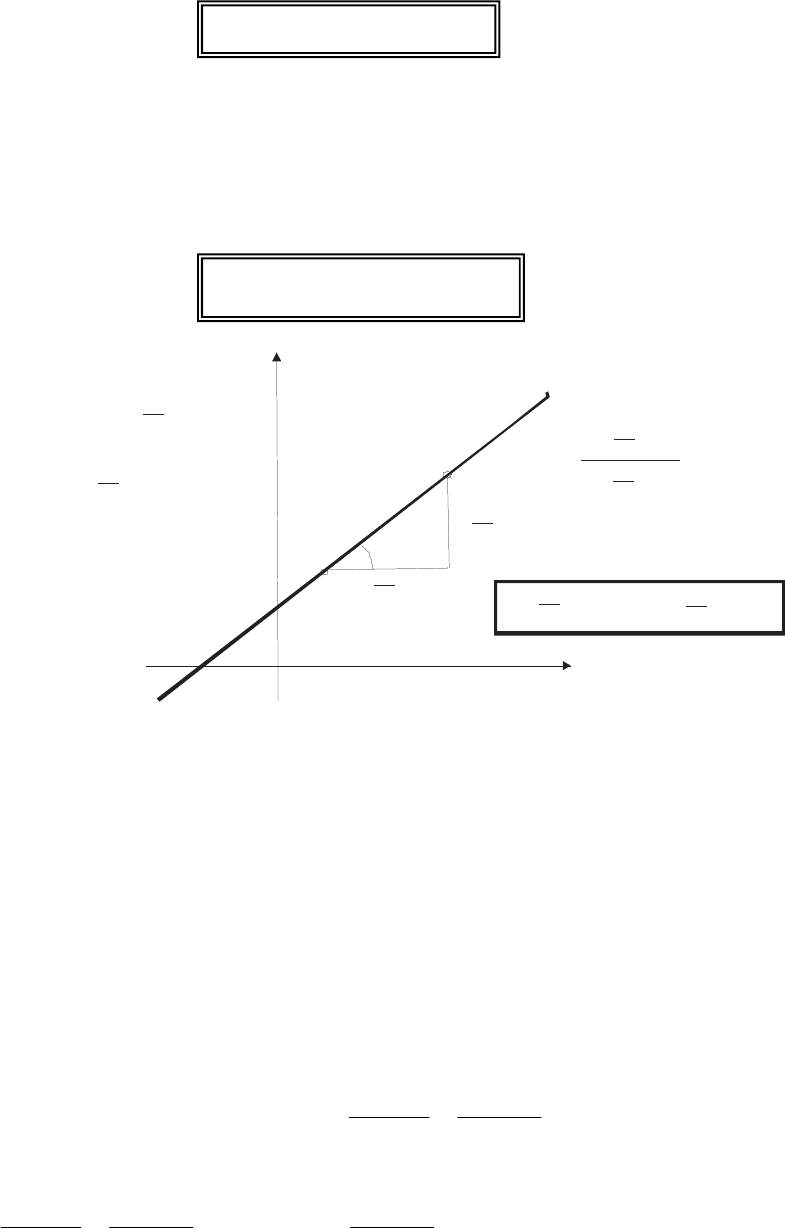
(рис.4), т.е.
k tg
α
=
. Если учесть, что тангенс острого угла есть величи-
на положительная, а тангенс тупого угла – величина отрицательная, то
можно очень быстро представить расположение прямой на плоскости
(рис.3). Заметим, что углом между прямой и положительным направлени-
ем оси
Ox
называют наименьший угол.
49
y=kx,
k=y/x,
y
y
x
x
κ= β<0tg
κ= α 0tg >
α
β
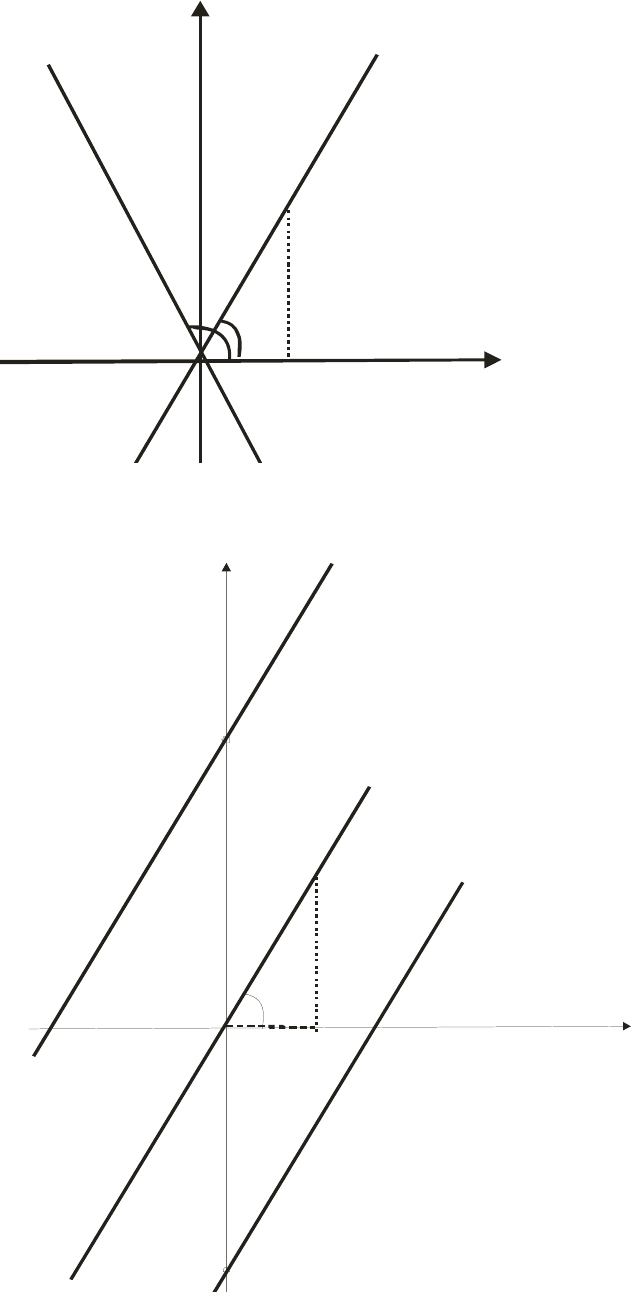
Рис. 4. Геометрический смысл углового коэффициента
k
y=kx,
y=kx+b
y=kx-b
k=y/x,
y
y
x
x
b
-b
κ= αtg
α
Рис. 5. Построение графика прямой
y kx b
= +

50
Прямая, заданная уравнением
y kx b
= +
, параллельна прямой, описан-
ной уравнением
y kx
=
. Коэффициент
b
есть величина отрезка, отсекаемо-
го прямой
y kx b
= +
на оси
.
Oy
Эта величина может быть как положитель-
ной, так и отрицательной. Для того, чтобы построить график прямой
y kx b
= +
, зная график прямой
y kx
=
, надо прямую
y kx
=
параллельно
поднять на величину
b
относительно начала координат, если
0
b
>
. Если
же величина
b
отрицательная, тогда прямую
y kx
=
надо параллельно
опустить на величину
b
относительно начала координат (рис. 5).
Общее уравнение прямой на плоскости
Линейное уравнение вида
0
Ax By C
+ + =
называется общим уравнени-
ем прямой на плоскости.
Если коэффициент
0
C
=
, то прямая, уравнение которой в этом случае
записывается
0
Ax By
+ =
, проходит через начало координат.
Важную роль выполняют коэффициенты
,
A B
. Вектор
(
)
;
n A B
r
, коор-
динатами которого являются эти числа, называется нормальным вектором
прямой, заданной уравнением
0
Ax By C
+ + =
.
Следует обратить внимание на тот факт, что
A
−
это проекция нор-
мального вектора
(
)
;
n A B
r
на ось
,
Ox
B
−
это проекция нормального век-
тора
(
)
;
n A B
r
на ось
.
Oy
Вектор
(
)
;
n A B
r
, начало которого совпадает с началом координат, за-
дает общее расположение прямой на плоскости: искомая прямая перпен-
дикулярна вектору
(
)
;
n A B
r
.
Взаимное расположение прямых на плоскости
На плоскости заданы прямые
1 2
,
L L
общими уравнениями:
1 1 1 1 2 2 2 2
: 0; : 0.
L A x B y C L A x B y C
+ + = + + =
Если выполнены условия
1 1 1
2 2 2
A B C
A B C
= =
, то прямые
1 2
,
L L
совпадают.
Если выполнены условия
1 1 1
2 2 2
A B C
A B C
= ≠
, то прямые
1 2
,
L L
параллель-
ны.
Векторы
(
)
(
)
1 2
1 1 2 2
; , ;
n A B n A B
r r
−
нормальные векторы прямых
1
L
и
2
L
соответственно.
Если скалярное произведение векторов
1
n
r
и
2
n
r
обращается в ноль,
т.е.
1 2
0,
n n
⋅ =
r r
то прямые
1
L
и
2
L
перпендикулярны.
51
Условие перпендикулярности прямых
1
L
и
2
L
в координатной форме:
Уравнение прямой, проходящей через точку, с заданным уг-
ловым коэффициентом
На плоскости дана точка
(
)
0 0 0
;
M x y
. Прямая, угловой коэффициент
k
которой задан, проходит через эту точку
(
)
0 0 0
;
M x y
(рис.6). Уравнение ее
имеет вид:
M
M
M
0
0
0
0
0
0
0
0
0
0
M
x
x
x
x
x
x
x
x
x
α
α
α
y
y
y
y
y
y
y
y
y
=
=
tg
tg
=
k
k
(
(
(
)
)
)
;
;
заданная
точка
точка
текущая
Рис. 6. Уравнение прямой, проходящей через заданную точку, с заданным угловым
коэффициентом
Уравнение прямой, проходящей через две заданные точки
На плоскости даны две точки
(
)
1 1 1
;
M x y
и
(
)
2 2 2
;
M x y
. Уравнение пря-
мой, проходящей через эти точки, очень легко написать. На прямой возь-
мем текущую, т.е. любую, точку
(
)
;
M x y
. Построим два вектора
(
)
1
1 1
;
MM x x y y
− −
uuuur
и
(
)
1 2 1 2 1
2
;
M M x x y y
− −
uuuuuur
. По построению эти векторы
коллинеарны. Условие коллинерности – это пропорциональность одно-
именных координат векторов:
1 1
2 1 2 1
x x y y
x x y y
− −
=
− −
.
Преобразуем эту запись:
( )
1 1 2 1
1 1
2 1 2 1 2 1
x x y y y y
y y x x
x x y y x x
− − −
= ⇒ − = −
− − −
.
1 2 1 2
0
A A B B
+ =
(
)
0 0
y y k x x
− = −
52
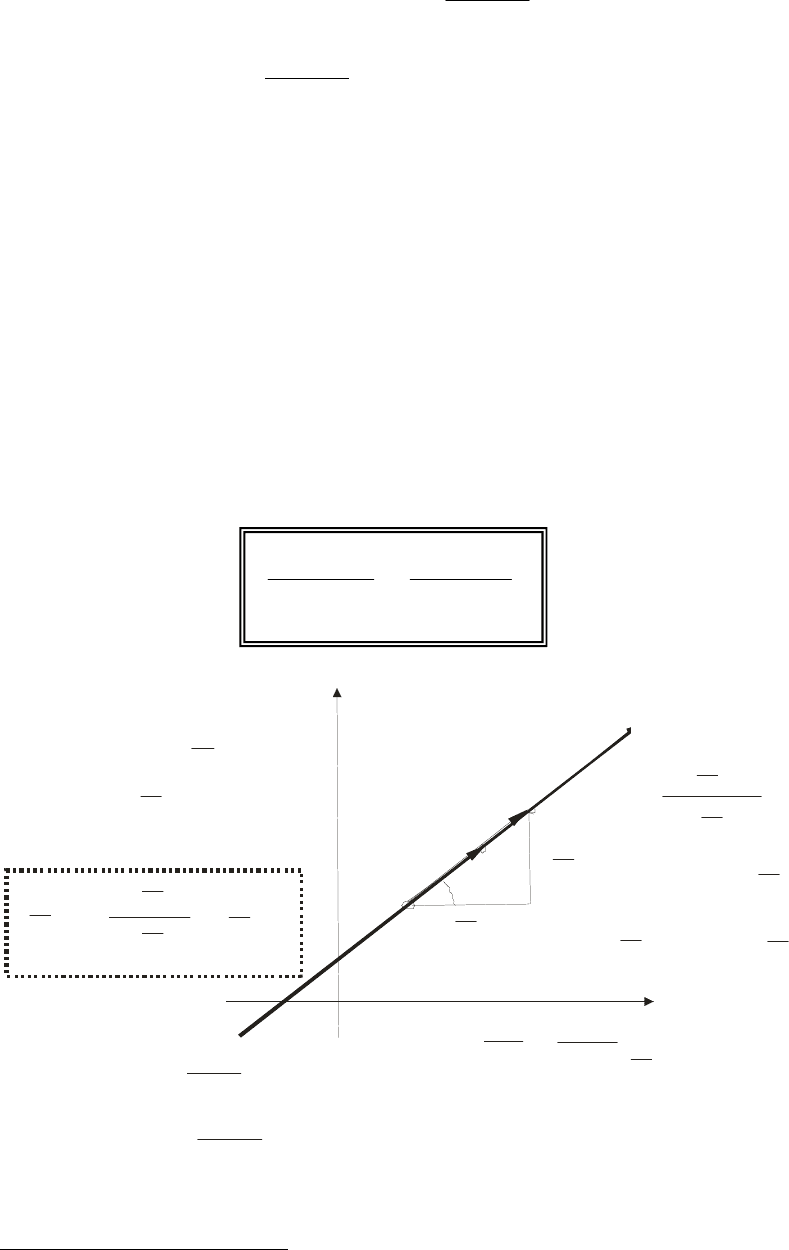
Из рис. 7 видно, что отношение
2 1
2 1
y y
x x
−
−
есть ни что иное как угловой
коэффициент
k
, т.е.
2 1
2 1
y y
k
x x
−
=
−
. Поэтому искомое уравнение можно на-
звать уравнением прямой, проходящей через заданную точку
(
)
1 1 1
;
M x y
с
заданным угловым коэффициентом
k
. В самом деле,
(
)
1 1
y y k x x
− = −
.
Возникает вопрос
, изменится ли уравнение прямой, если будем
считать ее проходящей через точку
(
)
2 2 2
;
M x y
с заданным угловым ко-
эффициентом
k
? Ведь в этом случае уравнение должны записать как
(
)
2 2
y y k x x
− = −
9
.
Уравнение прямой, проходящей через две точки
(
)
1 1 1
;
M x y
и
(
)
2 2 2
;
M x y
имеет вид
M
M
M
M
M
M
x
x x
x x
x
x
x
x
x
x
x
x
x
α
α
α
y
y
y
y
y
y
yy
y
y
y
y
y
y
=
=
=
tg
tg
k
k
(
(
(
(
(
)
)
)
)
)
;
;
;
заданные
точки
точка
текущая
1
1 1
1
1
1
1
1
1
1
1
1
1
1
2
2
2
2
,
угловой
коэффициент
=
2
2
Векторы ММ и М М
1
1
2
коллинеарны
М М =(x - x ; y - y )
1
1
2
2
М М =( x - x ; y - y )
1
1
2
1
Координаты
векторов
1
Уравнение прямой
через две
заданные точки
2
2
Уравнение прямой
с угловым коэффициентом
Рис. 7. Уравнение прямой, проходящей через две заданные точки М
1
и М
2
9
Согласно логическим рассуждениям, уравнение должно быть точно таким же. В противном случае
это будет вторая прямая. А здесь уже нарушается аксиома геометрии Евклида: через любые две раз-
личные точки проходит одна и только одна прямая.
1 1
2 1 2 1
y y x x
y y x x
− −
=
− −
