Суляндзига Е.П., Ушакова Г.А. Тесты по математике: Предел, производная, элементы алгебры и геометрии
Подождите немного. Документ загружается.

53
П р и м е ч а н и е . Уравнение прямой, проходящей через две точки
(
)
1 1 1 1
; ;
M x y z
и
(
)
2 2 2 2
; ;
M x y z
в пространстве R
3
имеет вид
Пример 41.
Найдите нормальный вектор прямой
3 2 6 0
x y
− + =
.
Решение
Прямая задана общим уравнением
3 2 6 0
x y
− + =
. Она не проходит че-
рез начало координат. Вектор
(
)
3; 2
n
−
r
является нормальным вектором
прямой, а это означает, что прямая перпендикулярна вектору
(
)
3; 2 .
n
−
r
Ответ
:
(
)
3; 2
n
−
r
− нормальный вектор прямой.
П р и м е ч а н и е . Общее уравнение
0
Ax By C
+ + =
для построения
прямой не является самым удачным. Большей частью решение задачи по-
строения такой прямой сводится к приведению общего уравнения к урав-
нению с угловым коэффициентом
y kx b
= +
. Однако есть одно красивое
представление прямой в виде так называемого уравнения в «отрезках».
Это уравнение позволяет не только быстро построить прямую, но и ре-
шить ряд других задач.
Уравнение прямой в «отрезках»
Предположим, прямая задана общим уравнением
0
Ax By C
+ + =
. Пола-
гаем, что в уравнении коэффициент
0
C
≠
. В противном случае задача уп-
рощается, так как прямая проходит через начало координат.
Выполним тождественные преобразования, проследите за ними:
( )
0 0 1
1 1.
A B
Ax By C Ax By C C x y
C C
x y x y
C A C B a b
+ + = ⇒ + = − ≠ ⇒ + = ⇒
− −
⇒ + = ⇒ + =
− −
Здесь введены обозначения:
; .
a C A b C B
= − = −
Обратите внимание
на уравнение
1
x y
a b
+ =
. Это и есть уравнение прямой «в отрезках». Воз-
никает вопрос, где эти отрезки?
Величина отрезка, который прямая
1
x y
a b
+ =
отсекает на оси
Ox
от на-
чала координат, равна
.
a
Действительно, чтобы найти точку пересечения
1 1 1
2 1 2 1 2 1
x x y y z z
x x y y z z
− − −
= =
− − −

54
прямой
1
x y
a b
+ =
и оси
Ox
(
0
y
=
− уравнение оси
Ox
), надо решить систему,
содержащую уравнения этих прямых:
1;
1 .
0.
x y
x
x a
a b
a
y
+ =
⇒ = ⇒ =
=
Аналогично можно показать, что величина отрезка, отсекаемого пря-
мой
1
x y
a b
+ =
на оси
Oy
(
0
x
=
−
уравнение оси
Oy
) от начала координат,
равна
.
b
И теперь, чтобы построить прямую, записанную уравнением в отрез-
ках”, надо в прямоугольной системе координат на оси
Ox
от начала коор-
динат отложить отрезок величины
,
a
на оси
Oy
от начала координат
−
отрезок величины
b
и, соединив их концы, получим искомый график за-
данной прямой.
Внимание
. В уравнении
1
x y
a b
+ =
дроби
x
a
и
y
b
должны быть со зна-
ками «+». Если появляются знаки «
−
», унесите их в знаменатели. Гово-
рим, что
a
и
b
−
это величины отрезков, а не длины. А это значит, что
a
и
b
могут быть не только положительными, но и отрицательными.
Пример 42.
Построить прямую
3 4 12 0
x y
− + =
.
Решение
Что можно сказать, глядя на заданное уравнение? Информации доста-
точно. Прямая описывается общим уравнением. Свободный коэффициент
не равен нулю
(
)
12
C
=
, следовательно, прямая не проходит через начало
координат. Вектор
(
)
3; 4
n
−
r
−
нормальный вектор этой прямой. Но нам нуж-
но построить график этой прямой.
Приведем общее уравнение прямой к уравнению в «отрезках». Про-
следите за преобразованиями.
3 4
3 4 12 0 3 4 12 1 1.
12 12 4 3
x y x y
x y x y
− + = ⇒ − = − ⇒ − = ⇒ + =
− − −
Итак, уравнение заданной прямой в «отрезках» имеет вид:
1
4 3
x y
+ =
−
.
Из него следует, что прямая отсекает на оси
Ox
отрезок, величина которо-
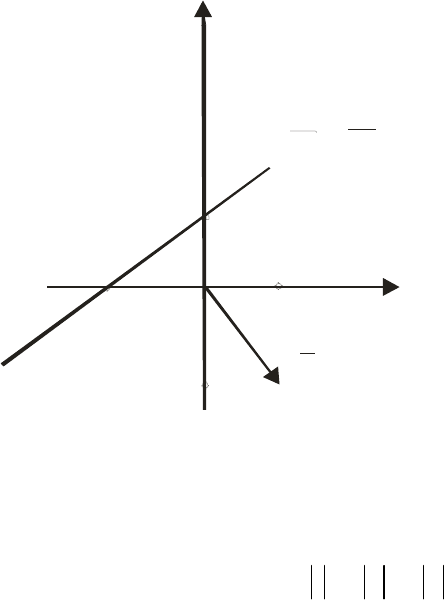
55
го равна
4
−
, т.е.
4,
a
= −
а на оси
Oy
−
отрезок, величина которого равна
3
,
т.е.
3
b
=
. В декартовой системе координат на оси
Ox
от начала координат
откладываем отрезок величины
4
−
. На оси
Oy
−
отрезок величины
3
. Со-
единяем концы этих отрезков и получаем искомый график прямой (рис. 8).
x
y
3
3
- 4
- 4
x
-4
y
3
=
1
+
n(3,-4)
- нормальный
вектор
Уравнение прямой
в отрезках“ ”
3x-4y+12=0
Общее
уравнение
прямой
Рис. 8. Прямая, заданная уравнением в “отрезках”
7. ВЕКТОРЫ
Рассмотрим векторы в трехмерном пространстве R
3
. Три единичных
вектора
, ,
i j k
r r r
образуют базис:
, 1.
i j k i j k
⊥ ⊥ = = =
ur uur uur
r r r
Любой четвертый вектор этого пространства можно представить в виде
разложения по базису
, ,
i j k
r r r
.
Предположим, имеем векторы
a
r
и
b
r
, которые в пространстве R
3
зада-
ны координатами (векторы этого пространства имеют три координаты)
(
)
1 1 1
; ;
a x y z
=
r
,
(
)
2 2 2
; ;
b x y z
=
r
.
Векторы
a
r
,
b
r
можно записать как разложения по базисным векторам
, ,
i j k
r r r
:
(
)
1 1 1 1 1 1
+ + ; ;
a x i y j z k x y z
= =
r r r r
,
(
)
2 2 2 2 2 2
+ + ; ;
b x i y j z k x y z
= =
r r r r
.
Очевидно, что координаты вектора
−
это проекции вектора на соответ-
ствующие оси.
Если говорят, что вектор задан как
1
2
M M
uuuuuur
, где
(
)
1 1 1 1
; ;
M x y z
−
первая
точка, начало вектора, а вторая точка
(
)
2 2 2 2
; ;
M x y z
−
конец вектора, то ко-
ординаты вектора
1
2
M M
uuuuuur
вычисляем как
2 1 2 1 2 1
, ,
x x y y z z
− − −
и заданный
56
вектор записывается
(
)
1 2 1 2 1 2 1
2
; ;
M M x x y y z z
= − − −
uuuuuur
или как разложение по
базису
(
)
(
)
(
)
1 2 1 2 1 2 1
2
.
M M x x i y y j z z k
= − + − + −
uuuuuur r r r
Длина вектора
a
r
вычисляется
2 2 2
1 1 1
a x y z
= + +
r
, длина вектора
1
2
M M
uuuuuur
находится как
( ) ( ) ( )
2 2 2
1 2 1 2 1 2 1
2
+ +
M M x x y y z z
= − − −
uuuuuur
.
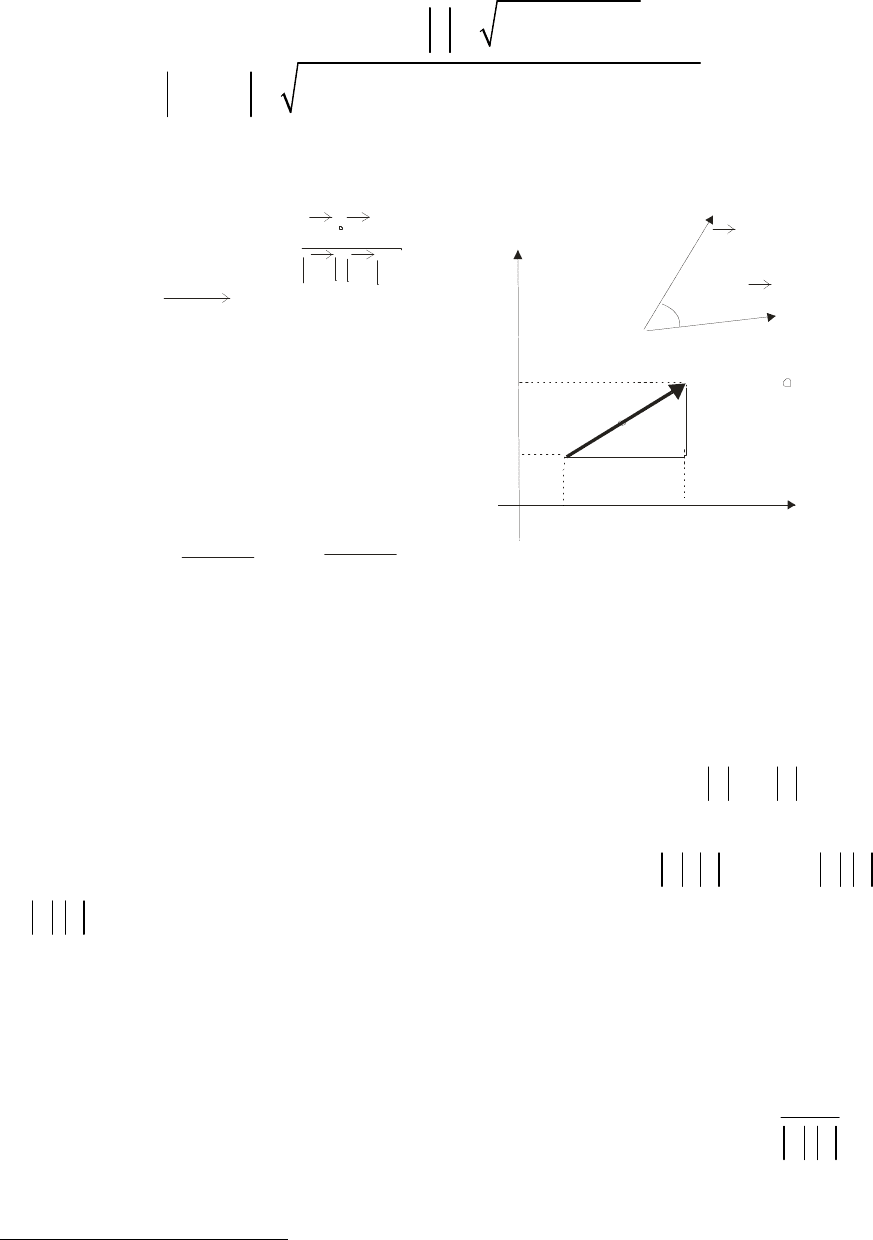
На рис. 9 рассмотрен случай задания векторов на плоскости (R
2
).
x
y
a
b
xx
x
y
y
y
M
M
- x
- y
α
cos =
α
a
a
b
b
M
M
M
M
M
M
=(x - x
;
y - y
)
M
0
M
0
x
x
x
x
y
y
y
y
y
2
2
1 12
2
0
0
- середина
отрезка
координаты
середины
(
)
;
0
0
,
-
=
=
0
0
++
x
;
отрезка
2
1
1
1
1
1
2
2
2
2
1
1
2
2
1
1
1
2
2
2
Рис. 9. Координаты вектора, середины отрезка и угол между
векторами на плоскости
Если векторы
a
r
и
b
r
заданы своими длинами
a
uur
и
b
ur
, и задан
угол
α
между ними, то
скалярное
10
произведение векторов
a
r
и
b
r
есть
число, которое записывается
a b
⋅
r r
и вычисляется как
a b cos a b cos
α α
⋅ ⋅ =
uur ur uur ur
;
a b a b cos
α
⋅ =
uur ur
r r
.
Если векторы
a
r
и
b
r
заданы своими координатами
(
)
1 1 1
; ;
a x y z
=
r
,
(
)
2 2 2
; ;
b x y z
=
r
, тогда их скалярное произведение записывается как
1 2 1 2 1 2
a b x x y y z z
⋅ = + +
r r
.
Угол между векторами определяется по формуле
a b
cos
a b
α
⋅
=
r r
uur ur
.
Условие перпендикулярности векторов
a
r
,
b
r
:
0.
a b
⋅ =
r r
10
Скаляр (с лат. scalaris) − величина, характеризуемая только числовым значением, например, дли-
на, объем, масса, плотность.
57
В результате
векторного
произведения векторов
a
r
и
b
r
получаем
новый третий вектор
c
r
(рис. 10), который обозначаем
a b
×
r r
, т.е.
c a b
= ×
r r r
и
для которого справедливы три утверждения:
1. Тройка векторов – правая. Векторы
a
r
,
b
r
,
c
r
(здесь вектор
a
r
– пер-
вый, вектор
b
r
– второй, вектор
c
r
– третий) образуют правую тройку, если
их привести к единому началу, а затем встать в конец третьего вектора,
т.е.
c
r
, тогда поворот первого вектора
a
r
ко второму вектору
b
r
осуществля-
ется в положительном направлении, т.е. в направлении против часовой
стрелки
11
.
2. Вектор
c
r
перпендикулярен плоскости, в которой лежат векторы
a
r
и
b
r
, а значит вектор
c
r
перпендикулярен вектору
a
r
и вектору
b
r
:
, ;
c a c b
⊥ ⊥
r r r r
3. Длина вектора
c
r
соизмерима с площадью параллелограмма, кото-
рый можно построить на векторах
a
r
,
b
r
. Записать это можно так:
c a b
= ×
ur
r r
.
Доказано, что площадь параллелограмма, построенного на векто-
рах
a
r
,
b
r
, вычисляется по формуле
.
парал
S a b sin
α
=
uur ur
, где
α
- угол, кото-
рый образуют векторы
a
r
и
b
r
. Следовательно, длина вектора может быть
определена по формуле:
c a b sin
α
=
ur uur ur
.
a
b
α
sin
α
a
b
x
y
z
c
c
=
a
b
c
c
,
a
b
c
,
,
правая тройка
векторов
О
x
a
b
c =
1)
2)
3)
Рис. 10. Векторное произведение
Если векторы
a
r
,
b
r
заданы в координатной форме
(
)
1 1 1
; ;
a x y z
=
r
,
11
Тень от вертикального предмета перемещается по часовой стрелке. Именно по этому принципу
устроены механические часы, так вращаются стрелки часов. Почему? Земля вращается в обратном на-
правлении. В этом же направлении она движется вокруг Солнца, как и все планеты солнечной системы.
Это естественное вращение и принято называть положительным, Направление по часовой стрелке - от-
рицательное.
58
(
)
2 2 2
; ;
b x y z
=
r
, то векторное произведение
a b
×
r r
вычисляется с помощью
символического определителя 3-го порядка, в котором первая строка -
единичные векторы базиса
, ,
i j k
r r r
, вторая строка – координаты первого
вектора
a
r
, а третья строка – координаты второго вектора
b
r
. Вычисляем
такой определитель, пользуясь свойством разложения определителя по
элементам первой строки, получим координаты третьего вектора
(
)
3 3 3
; ;
c x y z
=
r
.
1 1 1 1 1 1 1 1 1 1 1 1
1 1 1
2 2 2 2 2 2 2 2 2 2 2 2
2 2 2
; ; .
i j k
y z x z y z y z x z y z
c x y z i j k
y z x z y z y z x z y z
x y z
= = − + = −
r r r
r r r r
1 1 1 1 1 1
3 3 3
2 2 2 2 2 2
; ; .
y z x z y z
x y z
y z x z y z
= = − =
Тогда длина вектора
c
r
вычисляется как
2 2 2
3 3 3
.
c x y z
= + +
r
Приложение векторного произведение: площадь параллелограмма
S a b
= ×
r r
, и площадь треугольника
1
2
S a b
∆
= ×
r r
, построенных на векторах
a
r
,
b
r
.
Формулы вычисления скалярного и векторного произведений легко
получить, если выполнить перемножение векторов
a
r
,
b
r
, заданных в виде
разложения по базису
, ,
i j k
r r r
, и воспользоваться скалярным (табл.1) и век-
торным (табл.2) произведениями базисных векторов
, ,
i j k
r r r
. Обозначения
скалярного произведения − точка (⋅), векторного – крестик (
×
).
Табл. 1
Скалярное произведение (⋅) базисных векторов
, ,
i j k
r r r
⋅
i
r
j
r
k
r
i
r
1 0 0
j
r
0 1 0
k
r
0 0 1
59
Табл. 2
Векторное произведение
(
)
×
базисных векторов
, ,
i j k
r r r
×
i
r
j
r
k
r
i
r
0
k
r
−
j
r
j
r
−
k
r
0
i
r
k
r
j
r
−
i
r
0
Смешанное
произведение векторов
Смешанное произведение трех векторов
a
r
,
b
r
,
c
r
− это число, которое
обозначается
a b c
r r r
и вычисляется как определитель третьего порядка, где
в первой строке стоят координаты первого вектора, во второй
− координа-
ты второго, в третьей строке
− координаты третьего вектора.
Векторы
a b c
r r r
заданы координатами
(
)
1 1 1
; ;
a x y z
=
r
,
(
)
2 2 2
; ;
b x y z
=
r
,
(
)
3 3 3
; ;
c x y z
=
r
, тогда
1 1 1
2 2 2
3 3 3
.
x y z
a b c x y z
x y z
=
r r r
Возникают вопросы:
1) Можно ли строки в определителе переставлять местами?
2) Может ли быть смешанное произведение отрицательным?
3) Есть ли объяснения знака смешанного произведения векторов?
Приложения смешанного произведение:
1) Объем параллелепипеда, построенного на векторах
a
r
,
b
r
,
c
r
, приве-
денных к единому началу
V a b c
=
r r r
;
2) Объем пирамиды, построенной на векторах
a
r
,
b
r
,
c
r
, приведенных к
единому началу
1
6
V a b c
=
r r r
;
3) Условие компланарности векторов
a
r
,
b
r
,
c
r
:
0.
a b c
=
r r r
60
Пример 43.
Вычислить площадь треугольника, вершинами которо-
го являются точки
(
)
(
)
(
)
1; 1; 0 , 1; 1; 2 , 0; 1; 1 .
A B C
− − −
Решение
Построим два вектора
AB
uuur
и
AC
uuur
, исходящие из точки
(
)
1; 1; 0
A
−
. Коор-
динаты этих векторов:
(
)
2; 2; 2
AB = −
uuur
(
)
1; 0; 1
AC
= −
uuur
. Найдем
AB AC
×
uuur uuur
−
векторное произведение векторов
AB
uuur
и
AC
uuur
.
( )
2 2 2 2 2 2
2 2 2 2 4 2 2; 4; 2
0 1 1 1 1 0
1 0 1
i j k
AB AC i j k i j k
− −
× = − = − + = + + =
− −
−
r r r
uuur uuur r r r r r r
.
Найдем длину вектора
AB AC
×
uuur uuur
:
2 2 2 2 2 2 2 2 2
3 3 3
2 4 2 2 4 2 2 6.
AB AC x y z× = + + = + + = + + =
uuur uuur
Площадь треугольника, построенного на векторах
AB
uuur
и
AC
uuur
, находим
1
6
2
S AB AC
∆
= × =
uuur uuur
.
Ответ
:
6
S
∆
=
.
8. КРИВЫЕ ВТОРОГО ПОРЯДКА
Кривые второго порядка – это эллипс, окружность, гипербола и парабо-
ла.
Канонические уравнения кривых второго порядка, Nota Bene
12
:
2 2 2
x y R
+ =
−
окружность радиуса
R
, начало координат – центр сим-
метрии (рис. 11);
2 2
2 2
1
x y
a b
+ =
−
эллипс, осевая симметрия (рис. 11);
2 2
2 2
1
x y
a b
− =
−
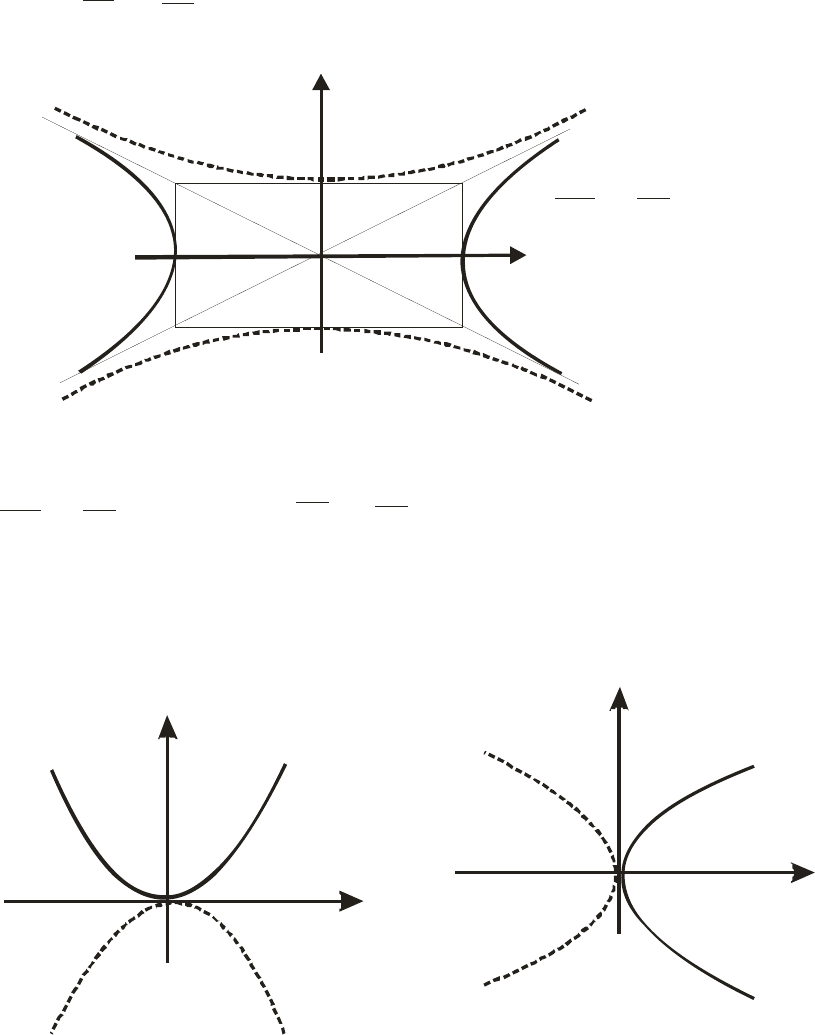
гипербола, пересекает ось
Ox
(рис. 12),осевая симметрия;
2 2
2 2
1
x y
a b
− + =
−
гипербола пересекает ось
Oy
, осевая симметрия (рис.
12);
12
NOTA BENE (лат. [нота бэ′нэ], обычно ставят пометку NB) – заметь хорошо.
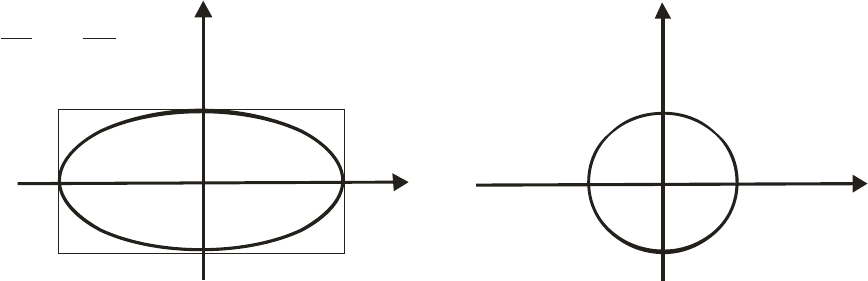
61
( )
2
2 0
y px p
= >
−
парабола,
p
−
параметр, вершина в начале коорди-
нат, ветви направлены вверх, ось
Oy
−
ось симметрии (рис. 13);
( )
2
2 0
y px p
= <
−
парабола,
p
−
параметр, вершина в начале коорди-
нат, ветви направлены вниз, ось
Oy
−
ось симметрии (рис. 13);
( )
2
2 0
x py p
= >
−
парабола,
p
−
параметр, вершина в начале коорди-
нат, ветви направлены вправо, ось
Ox
−
ось симметрии (рис. 13) ;
( )
2
2 0
x py p
= <
−
парабола,
p
−
параметр, вершина в начале коорди-
нат, ветви направлены влево, ось
Ox
−
ось симметрии (рис. 13) .
-a
a
b
-b
2
2
2
2
2
2
x
x
x
x
y
yy
y
a b
+
+
=1
= R
a
b -
- большая полуось
малая полуось
2
Рис. 11. Эллипс и окружность
Общее уравнение кривой второго порядка
2 2
0
Ax By Cx Dy E
+ + + + =
Заметим, что в этом уравнении отсутствует еще одно слагаемое
−
сла-
гаемое со второй степенью, содержащее произведение
xy
. Объяснить
этот момент можно следующим образом: общее уравнение кривой второго
порядка, не содержащее слагаемое с произведением
xy
, можно привести
к каноническому виду, выполняя элементарные линейные преобразования
выделения полных квадратов по переменным
x
и
y
и параллельным пе-
реносом системы координат. Если бы слагаемое с произведением
xy
при-
сутствовало в общем уравнении, то необходимо было бы еще выполнить и
поворот системы координат, что не является линейной операцией.
62
-a
a
b
-b
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
x
x
x
x
x
y
y
y
y
y
a
a
a
a
b
b
b
b
-
-
-
-
=1
=1
=1
=1
a
b -
- действительная полуось,
мнимая полуось
a
b -
- полуось,
полуось
мнимая
действительная
+
+
Уравнения
описывают сопряженные гиперболы
и
Рис. 12. Сопряженные гиперболы
y = 2px ,
p > 0
x = 2py ,
p > 0
y = 2px ,
p < 0
x = 2py ,
p < 0
2
2
2
2
x
x
y
y
Парабола,
ось симметрии - Оу
Парабола,
ось симметрии - Ох
Рис. 13. Параболы
Заметим, что по уравнению
2 2
0
Ax By Cx Dy E
+ + + + =
можно сразу
определить вид кривой второго порядка. В самом деле,
1) Если коэффициенты
A
и
B
равны (
A B
=
), то уравнение описывает
окружность;
