Суляндзига Е.П., Ушакова Г.А. Тесты по математике: Предел, производная, элементы алгебры и геометрии
Подождите немного. Документ загружается.

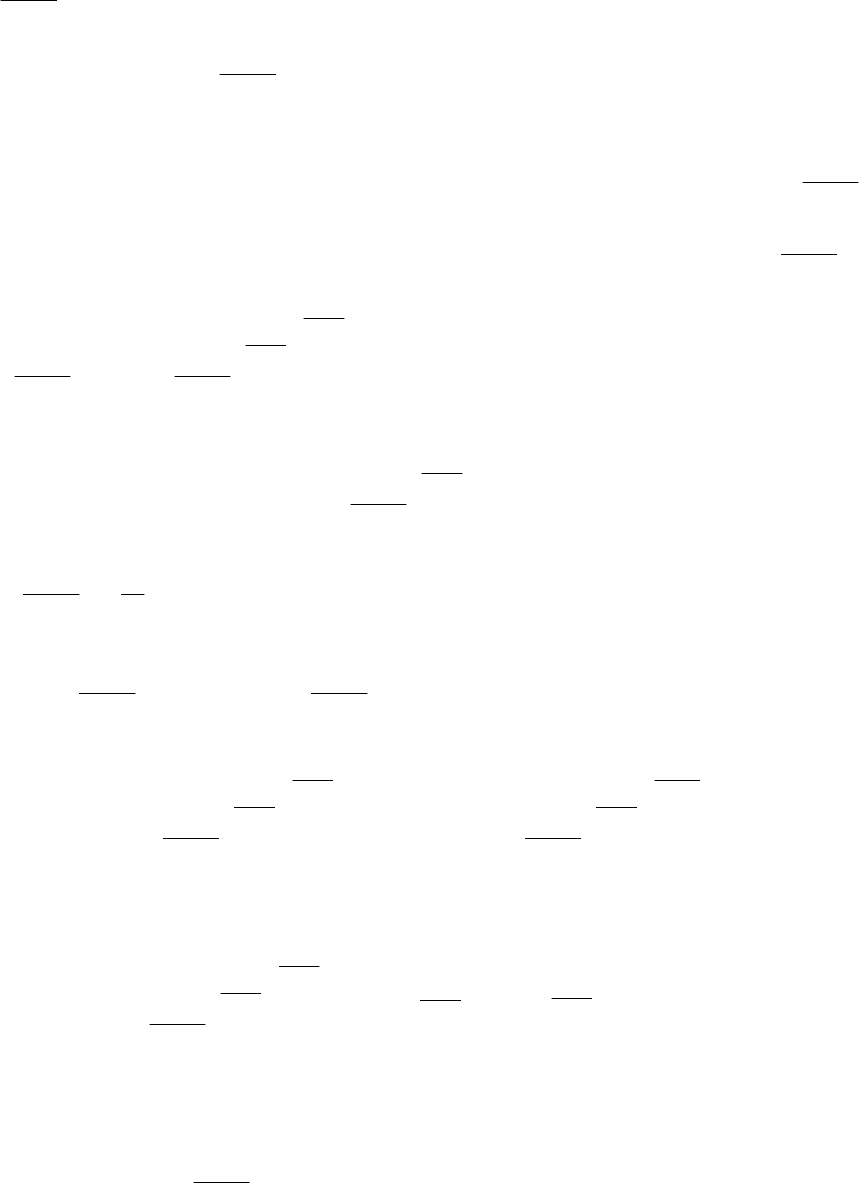
23
4
1
3
x
+
−
при
x
→ ∞
, видим, что имеем сумму единицы и бесконечно малой
величины,
4
lim 1 1
3
x
x
→∞
+ =
−
. Применим не столь сложные эквивалентные
алгебраические преобразования для того, чтобы в показателе получить
выражение, которое является обратным к бесконечно малой
4
3
x
−
. Ясно,
что такой величиной будет бесконечно большая
3
4
x
−
. Итак,
4
3
3
4
4 4
1 1
3 3
x
x
x x
−
−
+ = +
− −
. Если теперь возвратиться к исходной зада-
че, то, учитывая, что
( )
3
4
4
lim 1 1 ,
3
x
x
e
x
−
∞
→∞
+ = =
−
8
lim 8
3
x
x
x
→∞
∞
= =
− ∞
, получим:
2 2
2
4 4 2
3 3
3 3
4 4
8
3
8
3
8
lim
4
3
3
1 4
lim lim 1
3 3
4 4
lim 1 lim 1
3 3
4
lim 1 lim
3
x
x x
x x
x
x
x x
x x
x x
x
x
x
x
x
x
x
x x
x
x x
x x
e e
x
→∞
→∞ →∞
⋅
− −
− −
→∞ →∞
−
−
−
−
→∞ →∞
+
= + =
− −
= + = + =
− −
= + = =
−
8
.e=
Ответ
:
2
8
1
lim .
3
x
x
x
e
x
→∞
+
=
−
Рассмотрим еще один способ сведения предела ко второму заме-
чательному пределу
.
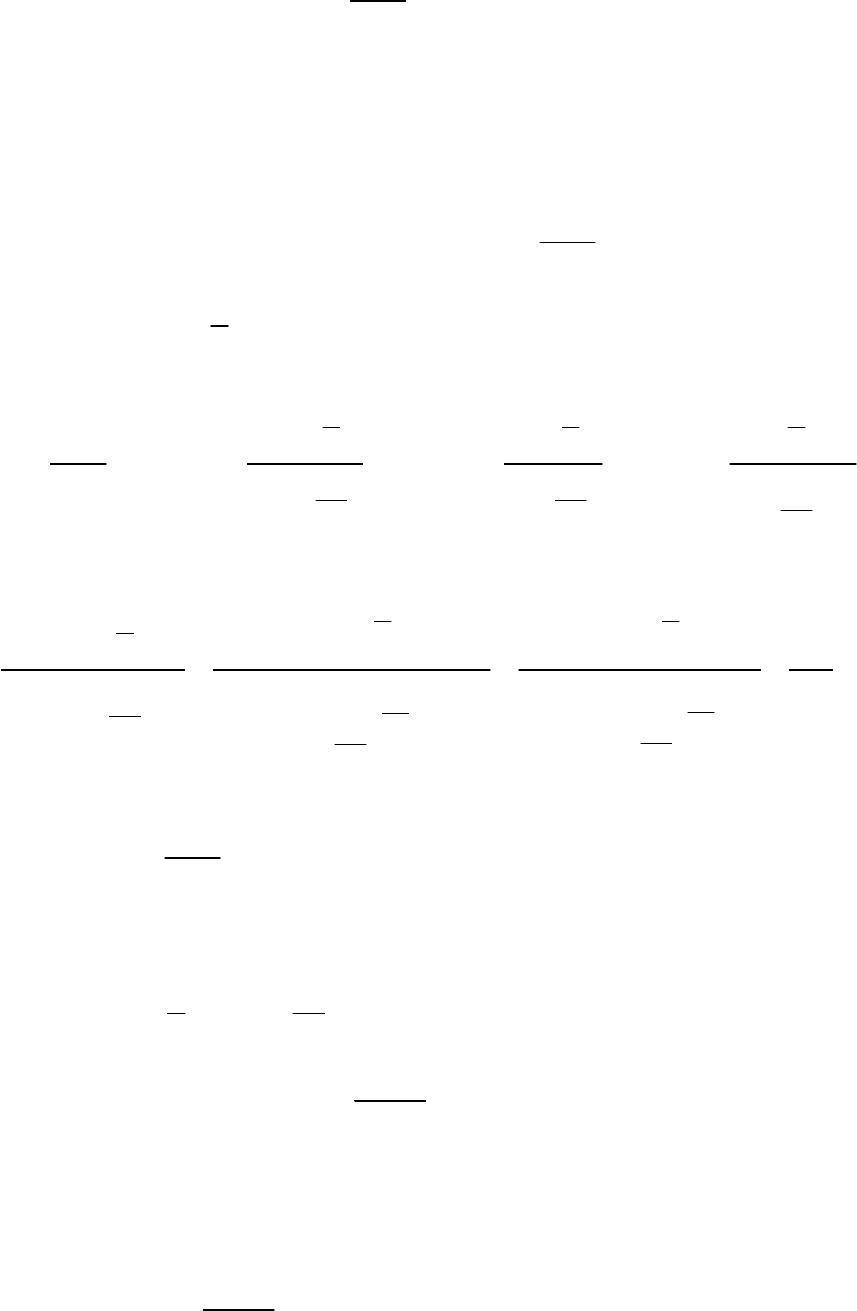
24
Пример 17
. Найти
2
1
lim
3
x
x
x
x
→∞
+
−
.
Решение
Рассмотрим задачу отыскания предела той же функции, что и в приме-
ре 16. Проследите за вычислениями. Возможно, что этот способ понравит-
ся больше.
Выполним преобразования над дробью
1
3
x
x
+
−
такие, чтобы получить
выражение вида
1
1
x
x
+
и в числителе, и в знаменателе.
2 2
2
2
2
1 1 1
1 1 1
1
lim lim lim lim
3 3
3
3
1 1
1
x x
x
x
x
x x x x
x
x
x x x
x
x
x x
x
→∞ →∞ →∞ →∞
+ + +
+
= = = =
− −
−
−
+ +
+
( )
2 2
2
2
8
2 6 6
3 2
3
3
1 1
1
lim 1 lim 1
lim 1
.
3
lim 1
3
3
lim 1
lim 1
x x
x
x x
x
x
x
x
x
x
x
x x
e
x
e
e
x
x
x
→∞ →∞
→∞
− −
− ⋅
−
−
→∞
→∞
→∞
+ +
+
= = = = =
−
+
−
−
+
+
Ответ
:
2
8
1
lim .
3
x
x
x
e
x
→∞
+
=
−
Заметили, как надо аккуратно работать, чтобы не потерять знак
«
−»?
3 3
3 1 1x x x
x x
−
− = − = +
.
Пример 18
. Найти
3 2
2 1
lim
2 5
x
x
x
x
−
→∞
+
+
.
Решение
Попытайтесь объяснить каждое действие.
Выпишем выражение, стоящее в круглых скобках, и найдем его предел
при
x
→ ∞
, т.е.
2 1
lim
2 5
x
x
x
→∞
+
+
.
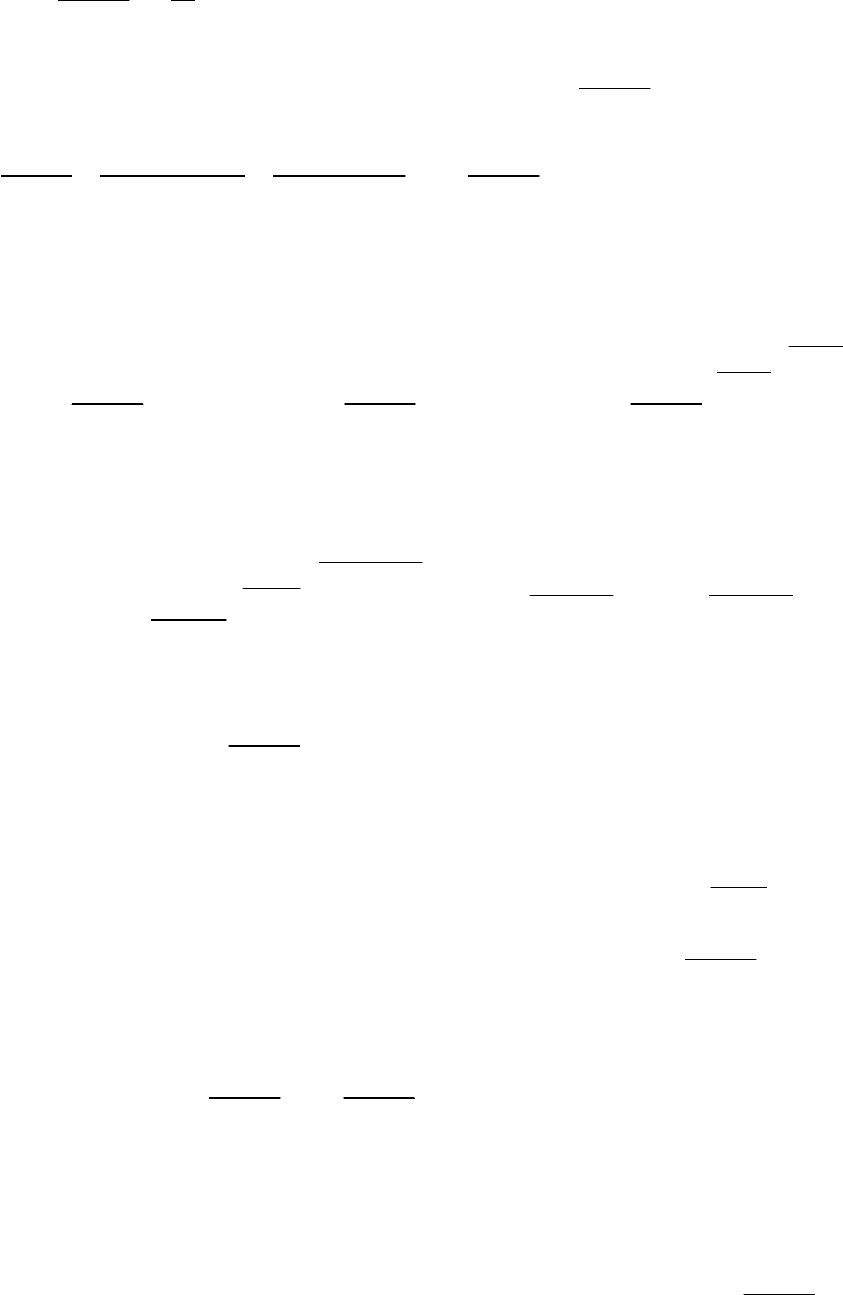
25
2 1
lim 1.
2 5
x
x
x
→∞
+ ∞
= =
+ ∞
Выполним преобразования над дробью
2 1
2 5
x
x
+
+
.
(
)
2 5 4
2 1 2 5 5 1 4
1 .
2 5 2 5 2 5 2 5
x
x x
x x x x
+ −
+ + − + −
= = = +
+ + + +
Теперь выполним эквивалентные преобразования над функцией, стоя-
щей за знаком предела.
( )
4
3 2
2 5
2 5
3 2 3 2
4
2 1 4 4
lim lim 1 lim 1
2 5 2 5 2 5
x
x
x
x x
x x x
x
x x x
−
⋅ −
+
+
− −
−
→∞ →∞ →∞
+ − −
= + = + =
+ + +
(
)
4 3 2
2 5
2 5
12 8 12 8
lim
4
6
2 5 2 5
4
lim 1 lim .
2 5
x
x
x
x
x x
x x
x x
e e e
x
→∞
− −
+
+
− + − +
−
−
+ +
→∞ →∞
−
= + = = =
+
Ответ
:
3 2
6
2 1
lim
2 5
x
x
x
e
x
−
−
→∞
+
=
+
.
П р и м е ч а н и е . Обратите внимание, что в скобках можно получить
как единицу
и плюс бесконечно малую величину (
4
1
3
x
+
−
, пример 16
)
, так
и единицу и минус бесконечно малую величину (
4
1
2 5
x
−
+
, пример 18
),
т. е.
алгебраическую сумму единицы и бесконечно малой величины. Во втором
случае знак «
−
» нужно обязательно учесть, для чего запишем его в числи-
теле дроби:
4 4
1 1
2 5 2 5
x x
−
− = +
+ +
. В противном случае его можно потерять,
и тогда решение будет неверным.
Рассмотрим еще один вариант решения данного примера. Ясно,
что так надо поступать только тогда, когда предел дроби, стоящей в скоб-
ках, будет равен единице. В нашем случае это так:
2 1
lim 1
2 5
x
x
x
→∞
+
=
+
.
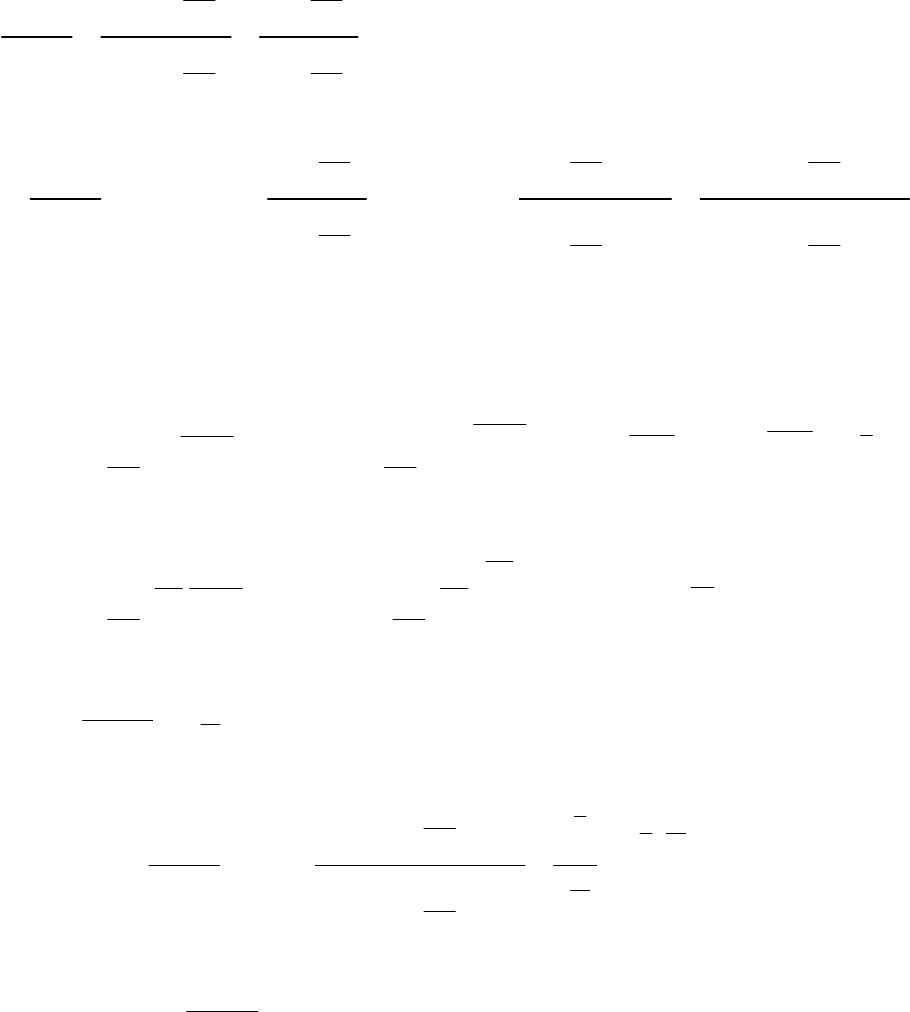
26
Решение
Выполним элементарные преобразования над дробью, стоящей в
скобках:
1 1
2 1 1
2 1
2 2
5 5
2 5
2 1 1
2 2
x
x
x x
x
x
x x
+ +
+
= =
+
+ +
. Переходя к исходному пределу, получим:
3 2
3 2 3 2
3 2
3 2 3 2
1 1 1
1 1 lim 1
2 1
2 2 2
lim lim lim
5
2 5
5 5
1
1 lim 1
2
2 2
x
x x
x
x
x x
x x x
x
x
x x x
x
x
x x
−
− −
−
→∞
− −
→∞ →∞ →∞
→∞
+ + +
+
= = =
+
+
+ +
.
Найдем отдельно пределы, стоящие в числителе и знаменателе соот-
ветственно.
3 2
3 2
3
2
2
2
3 2
3 2
2 2
lim
2
2
1 1
lim 1 lim 1 lim ;
2 2
x
x
x
x
x
x
x
x x
x
x
x x x
e e e
x x
−
−
→∞
−
−
→∞ →∞ →∞
+ = + = = =
( )
( )
( )
5
3 2
2
5 3 2
15
2
2
5
3 2
2 3 2 2
2
5 2 5
lim
5 5
lim 1 lim 1 lim
2 2
.
x
x
x
x
x
x
x x x
x
x
x x x
e
x x
e e
⋅ −
−
→∞
⋅ −
−
⋅
→∞ →∞ →∞
+ = + = =
= =
Итак,
3
3 15
2
2 2
15
2
3 2
3 2
6
3 2
1
lim 1
2 1
2
lim .
2 5
5
lim 1
2
x
x
x
x
x
x
x e
x
e e
x
e
x
−
−
−
→∞
−
−
→∞
→∞
+
+
= = = =
+
+
Ответ
:
3 2
6
2 1
lim
2 5
x
x
x
e
x
−
−
→∞
+
=
+
.
2. ПРОИЗВОДНАЯ
Сложная функция – это суперпозиция, т.е. композиция, функций.
Как научиться быстро и правильно дифференцировать сложную функ-
цию?

27
Надо предъявить к себе три простых требования и строго выпол-
нять их:
1. Правильно устанавливать порядок следования элементарных функ-
ций в соответствии с их приоритетами в композиции сложной функции.
2. Знать производные элементарных функций и правила дифференци-
рования алгебраической суммы, произведения и частного функций.
3. Знать формулу дифференцирования сложной функции.
П р и м е ч а н и я
1. Ошибок при нахождении производной не будет, если, называя про-
изводную некоторой элементарной функции, будете говорить: производ-
ная
−
это функция (называете ее)
того же самого аргумента
.
2. Определение порядка следования элементарных функций в компо-
зиции сложной функции напоминает разборку кочана капусты: снимаете
верхний лист, затем из оставшихся
−
снова верхний и так, пока не добере-
тесь до основания. Если возникают трудности при установлении порядка
следования функций, попытайтесь вычислить значение этой функции при
некотором фиксированном значении аргумента. Этот момент очень важен
при нахождении производной сложной функции.
3. Формулы и правила дифференцирования элементарных функций
изложены во всех учебниках математического анализа. Более того, шпар-
галка с производными и правилами дифференцирования пусть лежит на
столе у каждого обучающегося премудростям дифференцирования. Она
не поможет, если не уяснить формулу дифференцирования сложной
функции.
Получим формулу дифференцирования сложной функции. Оставим
все тонкости рассуждений и выполним преобразования.
Предположим, дана сложная функция
(
)
y f x
=
, изучив которую устано-
вили, сколько и какие элементарные функции ее образуют. Пусть это бу-
дут функции
(
)
(
)
(
)
(
)
, , ,
y f u u u v v v s s s x
= = = =
, т.е. сложную функцию
(
)
y f x
=
образуют четыре элементарные функции
, , ,
f u v s
.
В определении производной
'
0
lim
x
dy y
y
dx x
D ®
D
= =
D
участвует отношение
двух бесконечно малых величин: приращение функции
y
D
и приращение
аргумента
x
D
.
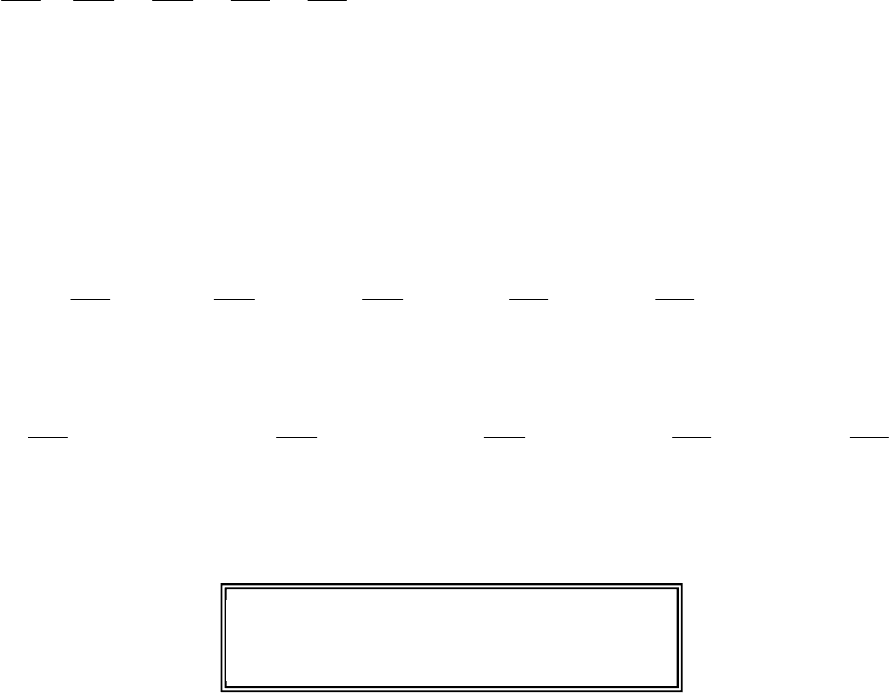
Рассмотрим это отношение
y
x
D
D
и выполним ряд простейших эквива-
лентных операции, не нарушающие общности рассуждений.
28
y y u v s
x u v s x
D D D D D
= Ч Ч Ч
D D D D D
.
Очевидно, такую цепочку множителей можно либо продолжить, либо
прервать. Длина этой цепочки, а именно, количество множителей в ней,
зависит от количества функций, составляющих сложную функцию.
Переходим в этом равенстве к пределу при условии
0
x
D ®
. Учитывая,
что функции
(
)
(
)
(
)
(
)
, , v , s
y y u u u v v s s x
= = = =
непрерывны и диффе-
ренцируемы по своим аргументам, получаем
0 0 0 0 0
lim lim lim lim lim
x u v s x
y y u v s
x u v s x
D ® D ® D ® D ® D ®
D D D D D
= Ч Ч Ч
D D D D D
.
Согласно определению производной можно записать:
' ' ' ' ' '
;
0 0 0 0 0
lim ; lim ; lim = lim = ; lim
x u v s x
x u v s x
y y u v s
y y y u v s
x u v s x
D ® D ® D ® D ® D ®
D D D D D
= = = =
D D D D D
При условии, что в сложной функции участвуют четыре элементарные
функции, производная такой функции может быть записана как
Пример 19.
Установите порядок следования элементарных функций,
начиная с внешней, участвующих в композиции функции
( )
2 3 .
y sin x= +
4
Решение
Можно сразу сказать, что элементарными функциями, участвующими в
образовании заданной сложной функции, являются линейная, степенная и
тригонометрическая функции.
Если возникают трудности определения составляющих функций, попы-
тайтесь провести вычисления сложной функции при некотором значении
аргумента. Выполним эту работу.
Положим
1.
x
=
Шаг 1
. Сначала вычислим
2 3
x
+
, это будет
2 1 3 5
Ч + =
. Первой и внут-
ренней является
линейная
функция
2 3
x
+
.
Шаг 2
. Затем вычислим
( )
2 3
x +
4
, получим
( )
4
4
2 1 3 5 625
Ч + = =
. Это вто-
рая функция,
степенная
.
Шаг 3
. И только сейчас можем вычислить при
1
x
=
значение функции
' ' ' ' '
u v s x
y y u v s
= Ч Ч Ч
29
( )
2 3sin x +
4
.
Это будет число
625 0.176.
sin
»
Тригонометрическая функ-
ция
− последняя функция в процессе вычисления значения сложной функ-
ции, она будет внешней.
Шаг 4
. Определим порядок следования функций, участвующих в обра-
зовании сложной функции, начиная с внешней и до внутренней. Это поря-
док, обратный порядку вычисления значения сложной функции. Именно
так надо устанавливать порядок для нахождения производной сложной
функции.
Проведя анализ полученных вычислений
, можно сделать вывод: в об-
разовании заданной сложной функции участвуют три элементарные функ-
ции. Порядок их следования, начиная с внешней, будет таким: тригоно-
метрическая, степенная, линейная.
Ответ
: Порядок следования функций, начиная с внешней: тригоно-
метрическая, степенная, линейная.
Пример 20
. Найти производную функции
( )
2 3
y sin x= +
4
.
Решение
В примере 19 определили порядок следования элементарных функций:
тригонометрическая
(
)
...
sin
, степенная
( )
...
4
и линейная
2 3
x
+
.
Заметим, что аргументом тригонометрической функции
(
)
...
sin
является
выражение
( )
2 3
x +
4
, аргументом степенной функции
( )
...
4
является ли-
нейное выражение
2 3
x
+
.
Производная
тригонометрической
функции
( ) ( )
... 2 3
sin sin x= +
4
будет
косинус того же аргумента, т.е.
( ) ( )
... 2 3
cos cos x= +
4
.
Производная
степенной
функции
( )
...
4
будет опять степенная функция,
но степень ее на единицу меньше, т.е.
( )
4 ...
3
. Заметим, что в круглых скоб-
ках находится выражение
2 3
x
+
, и производная в данном случае запишет-
ся как
( ) ( )
4 ... 4 2 3
x= +
3 3
.
Находим производную
линейной
функции
2 3
x
+
:
( )
'
2 3 2
x
+ =
.
Таким образом, производная заданной функции находится по формуле
' ' ' '
,
u v x
y y u v
= Ч Ч
т. е. в производной сложной функции будет столько мно-
жителей, сколько элементарных функций участвует в ее образовании, в
30
нашем случае – три:
( ) ( )
3
'
2 3 4 2 3 2.
y cos x x
= + Ч + Ч
4
Ответ
:
( ) ( ) ( ) ( )
3 3
'
2 3 4 2 3 2 8 2 3 2 3 .
y cos x x x cos x= + Ч + Ч = + +
4 4
Пример 21
. Найти производную функции
2
y cos x
=
Решение
Функцию
2
y cos x
=
можно записать как
( )
2
2
y cos x cos x= =
.
Здесь внеш-
ней функцией является степенная, возведение в квадрат. Далее следует
тригонометрическая функция
cos
x
. Сложную функцию образуют две эле-
ментарные функции: степенная
( )
2
...
и тригонометрическая
(
)
cos ...
. Произ-
водная заданной функции, согласно правилу дифференцирования слож-
ной функции, должна содержать произведение двух множителей: произ-
водную степенной функции и производную тригонометрической функции.
Производную
степенной
функции
( ) ( )
2 2
...
cos x
=
находим как
( ) ( ) ( )
1
2 ... 2 ... 2 2
cos x cos x
= = =
.
Производная
тригонометрической
функции
cos x
− это табличная про-
изводная:
( )
'
cos x sin x
= -
.
Таким образом, производную заданной сложной функции находим как
произведение
2
cos x
и
sin x
-
, т.е.
( )
'
2 .
y cosx sinx
= Ч-
Выполним преобра-
зования:
(
)
2 2 2 .
cosx sinx cos x sin x sin x
Ч- = - Ч = -
Производная сложной
функции примет вид
'
2 .
y sin x
= -
Ответ
:
'
2 .
y sin x
= -
Пример 22
. Найти производную функции
2
y cos x
=
Решение
Из задания функции ясно, что внешней является тригонометрическая
функция
( )
(
)
2
...
cos cos x
=
. Аргументом этой функции является степенная
функция
2
.
x
Заданную сложную функцию определяют две элементарные
функции: тригонометрическая
(
)
...
cos
и степенная
2
.
x
Сравните с функци-
ей примера 21, в этом случае порядок следования функций обратный.
Производная сложной функции будет содержать два множителя: про-
изводную тригонометрической функции и производную степенной функ-
ции.
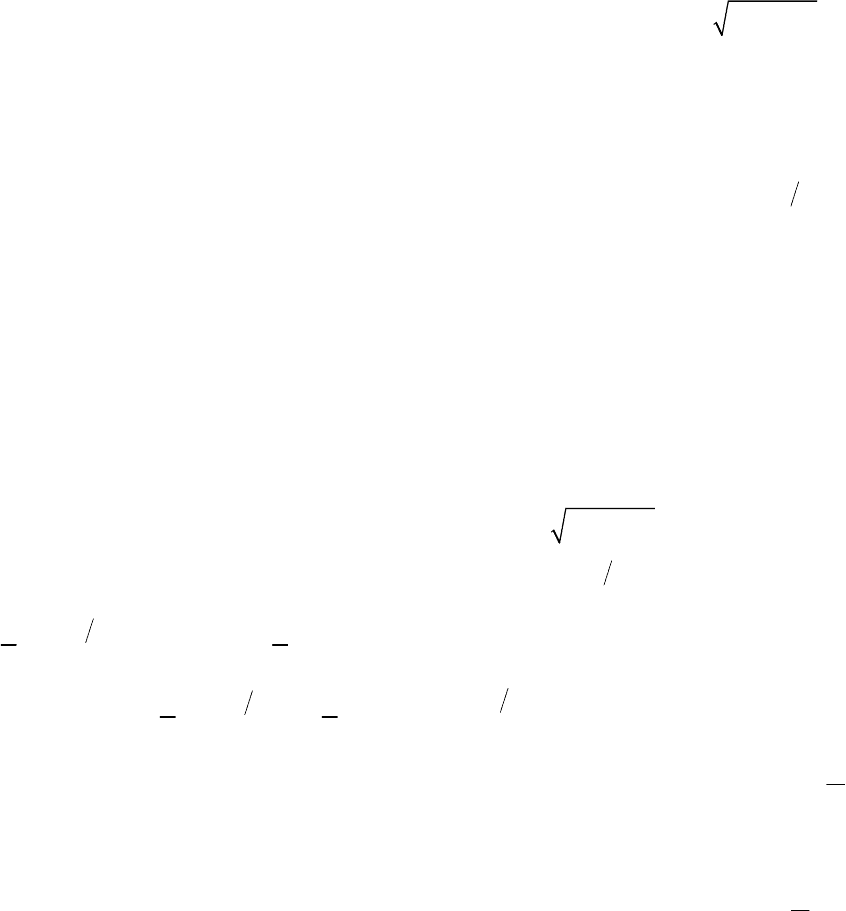
31
Продолжим решение задачи отыскания производной сложной функции.
Находим производную внешней
тригонометрической
функции
(
)
... .
cos
Это будет минус синус того же аргумента, т.е.
( )
(
)
2
... .
sin sin x
- = -
Производная
степенной
функции
2
x
:
( )
'
2
2
x x
=
.
Искомая производная равна произведению
(
)
2
sin x
-
и
2
x
, т.е.
(
)
(
)
' 2 2
2 2 .
y sin x x x sin x
= - Ч = -
Ответ
:
' 2
2 .
y x sin x
= -
Пример 23
. Найти производную функции
( )
3
3 5
.
ln x
y e
-
=
Решение
Заданная функция – это суперпозиция четырех элементарных функций:
показательной, степенной, логарифмической и линейной.
Показательная функция:
( )
...
e
,
степенная функция:
( )
1 3
...
, логарифми-
ческая функция – натуральный логарифм:
(
)
...
ln
, линейная функция:
3 5
x
-
.
Производная данной сложной функции – это произведение четырех
множителей: производной показательной, производной степенной, произ-
водной логарифмической и производной линейной функций. Найдем про-
изводные перечисленных функций.
Производная
показательной
функции
( )
...
e
есть та же показательная
функция с тем же аргументом, т.е.
( )
( )
3
3 5
...
.
ln x
e e
-
=
Производная
степенной
функции
( )
1 3
...
есть степенная функция
( )
2 3
1
... .
3
-
В степень
1
3
возводится
(
)
3 5
ln x
-
, поэтому производная записы-
вается как
( ) ( )
( )
2 3
2 3
1 1
... 3 5
3 3
ln x
-
-
= - .
Производная
натурального логарифма
(
)
...
ln есть дробь
1
...
, т.е. вели-
чина, обратная аргументу (единица, деленная на аргумент). В нашем слу-
чае аргументом натурального логарифма является линейное выражение
3 5.
x
-
Поэтому производная натурального логарифма
1
...
примет вид

32
1
3 5
x
-
, т.е.
1 1
... 3 5
x
=
-
.
Находим производную
линейной
функций
3 5
x
-
:
( )
'
3 5 3
x
- =
.
Производная сложной функции примет вид:
( )
( )
2 3
...
'
1 1
... 3
3 ...
y e
-
= Ч Ч Ч
.
Учитывая аргумент каждой составляющей функции, запишем искомую про-
изводную
( )
( )
( )
( )
( )
( )
3
3
2
3 5
'
3
2
3 5
3
1 1
3 5 3 =
3 3 5
1
= 3 5 .
3 5
ln x
ln x
y e ln x
x
e ln x
x
-
-
-
-
= Ч Ч - Ч Ч
-
Ч - Ч
-
Ответ
:
( )
( )
( )
3
2
3 5
'
3
1
3 5 .
3 5
ln x
y e ln x
x
-
-
= Ч - Ч
-
Дифференцирование функции
( )
1
y
f x
= .
Прежде чем находить производную обратной функции
7
( )
1
y
f x
= , вы-
полним преобразование
( )
( )
( )
1
1
y f x
f x
-
= = . Теперь внешней функцией
является степенная функция, производная которой записывается
( )
( )
( ) ( )
( )
( )
( )
'
1 2 '
' 1
y f x f x f x
ж ц
- -
ч
з
= = - Ч
ч
з
ч
з
и ш
.
Пример 24
. Найти производную функции
5
1
8 3
y
x
=
+
.
Решение
. Преобразуем функцию
( )
1
5
5
1
8 3
8 3
y x
x
-
= = +
+
. Теперь про-
изводную надо взять сначала от степенной функции
( )
1
5
...
-
, затем от ли-
нейной
8 1
x
+
. Производная запишется
( ) ( )
6
1
5 5
'
'
1
8 3 8 3 8
5
y x x
-
-
ж ц
ж ц
ч
ч
з
з
ч
ч
з
з
= + = - + Ч
ч
ч
з
з
ч
ч
з
з
ч
ч
ч
ч
з
з
и ш
и ш
.
7
Нежелательно находить производную такой функции как производную частного. Почему? Дога-
дайтесь.
