Стрекалов А.В. Математические модели гидравлических систем для управления системами поддержания пластового давления

Подождите немного. Документ загружается.

601

Градиент целевой функции (6.10–6.11) может быть вычислен толь-

ко по разностной схеме, причем, для повышения точности можно ис-

пользовать «четырехточечную формулу» [250]. Если учитывать огра-

ничения области определения аргументов, то можно использовать ал-

горитм L-BFGSB [251].

К сожалению, в данной работе нет возможности привести деталь-

ное описание работы дан-

ного алгоритма, так как эт

является отдельным на-

правлением вычислитель-

ной математики. Рассмот-

рим результаты оптимиза-

ции согласно решению за-

дачи (6.10) на примере

МТГС, отображенной на

рис. 6.1, комплексные пока-

затели которой до оптими-

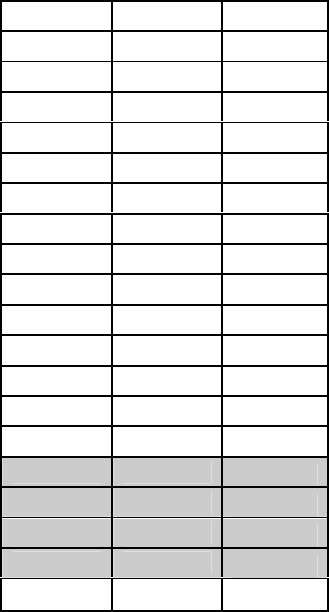
зации отражены в табл. 6.1.

В частности, коэффициен-

ты:

=148.7, К

эфф

=0.14.

Номинальная приеми-

стость скважин задана со-

гласно требуемой по техно-

логии заводнения: средней

– 1000 м

/сут, верхней –

300 м

/сут, и нижней –

200 м

/сут. После оптими-

зации, т.е. решения задачи

(6.11), имеем уже оптими-

зированную модель ТГС

(см. рис. 6.42) с искомыми

диаметрами штуцеров

(сверху вниз по схеме) –

=0.0057 м, d

=0.0111 м,

=0.0059 м и корректи-

рующими коэффициентами

АСГ (сверху вниз по схеме)

– kQ

=0.150, kdP

=0.890, kQ

=0.149, kdP

=0.91, kQ

=0.151, kdP

=0.890.

Комплексные показатели оптимизированной ТГС приведены в табл.

Таблица 6.6. Комплексные показате-

ли оптимизированной гидросистемы

(см. рис. 6.42)

Величина Ед.изм. Значение

кВт

343.49

ц0

кВт

59.77

кВт

550.68

кВт

302.2

г.н

. кВт

245.08

вх

кВт

17.36

вых

кВт

319.56

гео

кВт

282.5

вх0

кВт

17.36

вых0

кВт

35.84

кВт

179.66

63.03

д.е.

1.3

гс

58.64

37.57

фг

32.59

0.08

эфф

д.е.

464.75

∑

тыс.м

/сут

1.5

602

6.6. Как видно из таблицы, полный к.п.д. ТГС –

существенно вы-

рос: с 21.44 до 37.57%, а относительное отклонение

упало до пре-

небрежимо малого числа – 0.08%. Потребляемая АСГ электрическая

мощность упала с 2973.26 до 550.68 кВт. Такие великолепные показа-

тели являются руководством к соответствующей замене АСГ и штуце-

ров. Причем, гидравлическая характеристика заменяемых АСГ должна

соответствовать полученной в результате подбора корректирующих

коэффициентов kQ и kdP согласно (6.12–6.14).

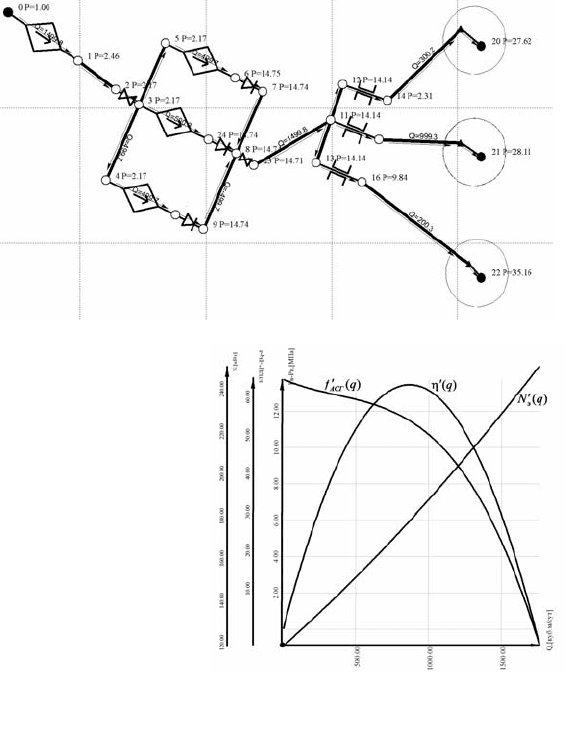
Рис. 6.42. Схема потокораспределения модели ТГС после оптимизации

Так как корректи-

рующие коэффициенты

kQ и kdP для всех АСГ

примерно равны, то ха-

рактеристики всех АСГ

на кустовой станции

должны соответство-

вать найденной (опти-

мальной). На рис. 6.43

показаны кривые опти-

мальной гидравличе-

ской характеристики

АСГ, к которой необхо-

димо привести факти-

ческие характеристики

для достижения опти-

Рис. 6.43. Кривые гидравлических характери-

стик АСГ, полученные в результате оптимиза-

ции

603

мального состояния системы, т.е. комплексных показателей в табл. 6.6.

Такую характеристику можно подобрать посредством формирова-

ния структуры КНС и выбора АСГ из предлагаемых типоразмеров. За-

дача автоматического подбора типоразмеров АСГ и структуры КНС

пока остается открытой для будущих решений. Однако, согласно опы-

ту автора данной работы, она не должна вызвать особых зат

руднений.

Естественно, точный подбор гидравлических характеристик АСГ,

соответствующих найденным при оптимизации, невозможен. Поэтому

придется обойтись лишь стремлением к максимально точному при-

ближению. Таким образом, после нахождения тех-показателей d, kQ и

kdP остается только сменить диаметры штуцеров на найденные и по-

добрать насосные агрегаты в соответствии с найденными оптималь-

ными ха

рактеристиками в реальной ТГС для достижения комплексно-

го оптимума: максимизации к.п.д. системы и минимизации отклонений

приемистостей нагнетательных скважин от требуемых по технологии

заводнения.

В заключение данного раздела следует отметить, что в случае,

когда предполагается оптимизировать ТГС посредством корректи-

рующих коэффициентов kQ и kdP одной КНС, характеристику которой

возможно привести к од

ному АСГ с суммарной гидравлической харак-

теристикой, решение (6.10) или (6.11) можно свести к более простой

задаче. В такой задаче предполагается наличие одного АСГ, т.е. M = 1.

При этом количество искомых диаметров штуцеров – N может быть

любым. Решение поиска оптимума сводится к прогонке целевой функ-

ции от двух аргументов –

⎟

⎠

⎞

⎜

⎝

⎛

эфф

kdP

, где k – номер звена АСГ, объе-

диняющего характеристику КНС. При этом до расчета целевой функ-

ции решается задача (6.4) подбора штуцеров. Т.е. значения целевой

функции при различных значениях аргументов всегда будут отражать

состояние ТГС, соответствующее заданным номинальным расходам в

нагнетательных скважинах. Таким образом, после расчета целевой

функции, например, в интервале

]1..1.0[∈

kdP

с ша-

гом 0.1 получим сеточную поверхность 10×10, максимум которой

можно найти методом простой прогонки. Для решения такой задачи в

данном примере, если не учитывать тепловые процессы, необходимо

21010 NI

⋅⋅×× решений задачи потокораспределения в виде (4.4)

или (4.26), где N – количество штуцеров/нагнетательных скважин, I

–

604

количество итераций при решении (6.4),

2 NI

⋅⋅ – количество вы-

числений потокораспределения для решения (6.4). Если учитывать

тепловые процессы (схема алгоритма на рис. 4.27), то количество вы-

числений составляет

21010 NIJ

⋅⋅⋅×× , где

J – количество

итераций, необходимое для расчета термораспределения. Например,

для МТГС Северо-Покурского месторождения, состоящей из 1461 зве-

на и 1415 узлов, время расчета комплексного потокораспределения со-

ставляет 5 секунд (для ПК–AMD3200+), а время решения такой задачи

при

I ≈ 4, N = 212 равно 20802122410105

≈⋅⋅⋅××c сут. Без

учета тепловых процессов время расчета одного потокораспределения

составляет примерно 0.7 с, а время расчета –

2912122410107.0

≈⋅⋅⋅××c

сут. Естественно, это является неприемле-

мым, поэтому к решению задачи оптимизации в таком виде следует

прибегать, например, при N < 30 (время расчета –

8.5302410107.0

≈⋅⋅⋅××c

сут) или для более малых по структуре

МТГС без учета тепловых процессов. Стоит отметь, что для решения

таких серьезных задач следует использовать специализированные

ЭВМ.

6.4. Особенности использования предлагаемой модели гидросистем

продуктивных пластов

В данном разделе рассматриваются примеры использования рас-

смотренной в четвертой главе модели ГПП посредством вычислитель-

ного эксперимента над моделью с различными условиями: учет фор-

мирования трещин, изменения проницаемости от давления, нарушения

закона Дарси, вариации случайного распределения проницаемостей и

т.п. в условиях работы нагнетательных и добывающих скважин в огра-

ниченном пласте. Эк

сперименты будем ставить на пласте Б6 со сред-

ней АО= –2057 м и толщиной 9.8 м. Все скважины условно полагаем

совершенными по степени и характеру вскрытия. Рассмотрим наибо-

лее простой пример расчета распределения ФЭС в модели ГПП участ-

ка пласта Б6 без учета трещинообразования и изменения проницаемо-

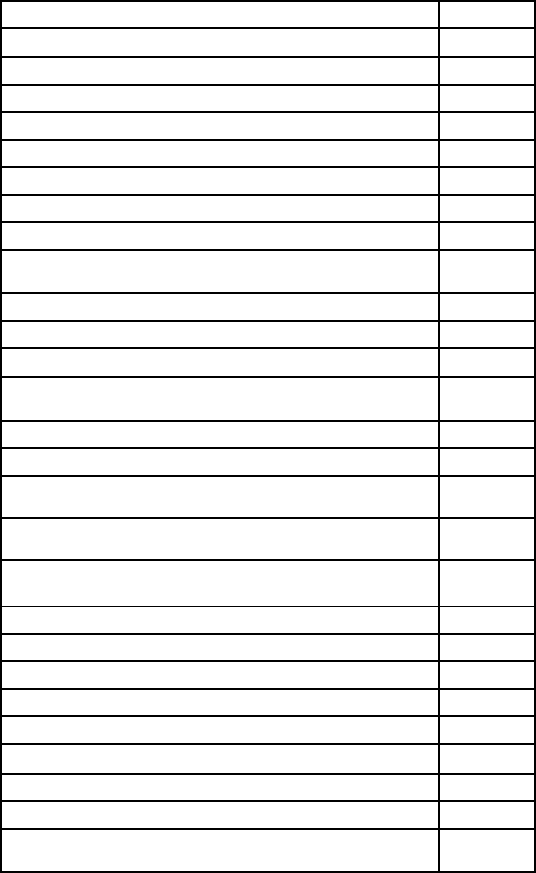
сти от давления. В табл. 6.7 пр

иведены исходные настройки модели.

605

Таблица 6.7. Параметры модели ГПП без учета трещин

и изменения проницаемости от давления

Количество слоев 10

Анизотропия –

)Z(

)Y,X(

,[д.е.]

0.13

Плотность нефти при P

, [кг/куб.м] 850

Плотность воды при P

, [кг/м

] 990

Вязкость нефти при P

, [мПа⋅с]

2.3

Вязкость воды при P

, [мПа*с] 1

Сжимаемость нефти – w

, [1/ГПа] 3.4

Сжимаемость воды – w

, [1/ГПа] 1.2

Сжимаемость породы – w

, [1/ГПа] 0.085

Открытая пористость при начальных условиях – m

отк

[%]

Нач. пластовое P

, [МПа] 20.4332

Начальная средняя нефтенасыщеннность – н

, [д.е]

Средняя проницаемость –

)Y,X(

, [мД]

16.5–27.5

Коэфф. изменения проницаемости от давления – n,

[д.е.]

0.051

Учитывать изменение проницаемости от давления Нет

Учитывать трещинообразование Нет

Градиент разрыва по X –

)X(

, [МПа/м]

0.10

Градиент разрыва по Y –

)Y(

, [МПа/м]

0.10

Градиент сдвига

н,в

dp , [МПа/м]

0.0001

Коэфф. расширения трещины – А

, [мм/д.е.] 10

Мин. толщина сомкнутой трещины – А

, [мм] 2

Проницаемость трещины – k

тр

, [мД] 50000

Коэфф. раскрытия трещины – D , [1/МПа] 12

Учитывать нарушение закона Дарси Нет

Коэфф.нелинейности –

, [д.е.]

–0.5

Критическое число – Re, [д.е.] 5

Горное давление P

, [МПа] 20.4332

Вариация проницаемости по распределению Гаусса,

[%]

606

а) б)

в)

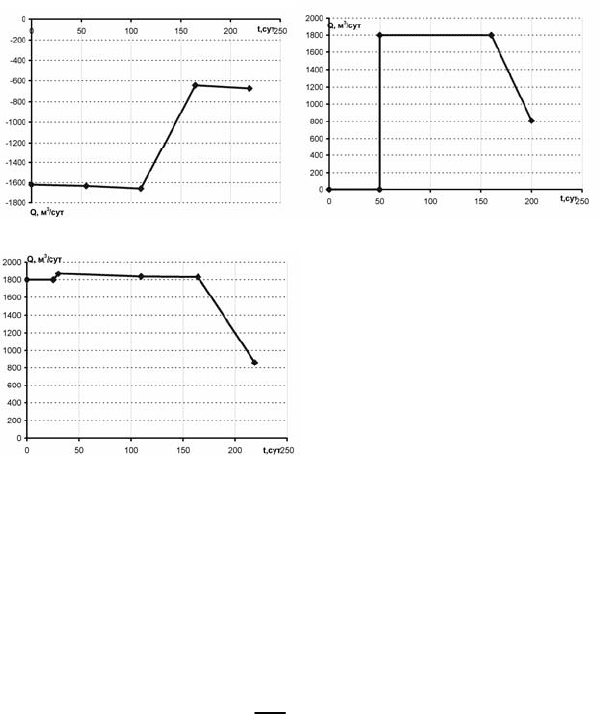
На рис. 6.45 – а, б показана динамика расходов жидкости в стволах

добывающей и нагнетательной скважины, выбранная в качестве гра-

ничных условий – Q(t) для данной модели. Проведя вычислительный

эксперимент, получим динамику ФЭС: на рис. 6.46 показана зависи-

мость забойного давления в добывающей и нагнетательной скважине

от времени. Как видно из рис. 6.46 – а, забойное да

вление добываю-

щей скважины снижается до времени 55 сут. Далее вследствие пуска

нагнетательной скважины в момент t = 50 сут возмущение доходит до

добывающей скважины, и забойное давление начинает расти с при-

мерно равным отношением

. После снижения приемистости с

t = 160 сут скорость роста забойного давления в добывающей скважи-

не снижается.

Рис. 6.45. Динамика приемистости и

дебита добывающей и нагнетательной

скважин:

а – добывающая скважина;

б – нагнетательная с пуском через 50

сут; в – нагнетательная в работе от на-

чала

607

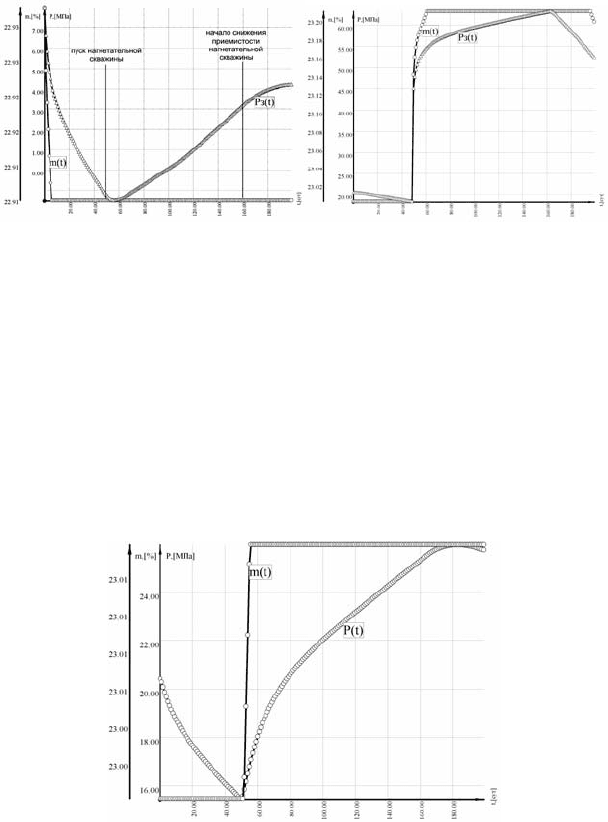
а) б)

Рис. 6.46. Динамика забойного давления:

а – в добывающей; б – в нагнета-

тельной скважине

Интервалы изменения давления на середине расстояния между

скважинами значительно меньше, чем самих скважинах (см. рис.

6.47). Возмущение от нагнетательной скважины до точки пласта, со-

ответствующей середине расстояния между скважинами, доходит

раньше, чем до добывающей скважины –

t = 52 сут. На рис. 6.48/1, 2

показана динамика пластового давления и открытой пористости пла-

ста в среднем слое –

l = 5. Как видно из распределения давления, во-

круг скважин формируются всем известные воронки депрессии и ре-

прессии. Причем, вследствие того, что нагнетательная скважина рабо-

тает с большим расходом и давлением, ее ЗВС имеет больший радиус.

Рис. 6.47. Динамика давления на середине расстояния

между скважинами

608

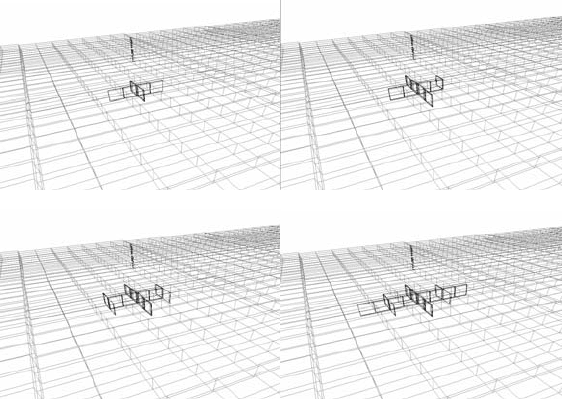
2 сут 6 сут

31 сут 51 сут

Рис. 6.48/1. Распределение пластового давления при работе нагнетательной и

добывающей скважины в ограниченном пласте Б6 размером ≈2000×1000 м (за-

ливка по давлению): минимальное давление –

min

=1.43 МПа, максимальное

давление –

max

=57.9 МПа

71 сут 150 сут

200 сут

отк

– 200 сут

(заливка по открытой пористости)

Рис. 6.48/2. Распределение давления при работе нагнетательной и добывающей

скважины в ограниченном пласте Б6 размером ≈2000×1000 м: минимальное

давление – P

min

=1.43 МПа, максимальное давление – P

max

=57.9 МПа; мини-

мальная открытая пористость –

отк

min

=22.91 %, максимальная –

отк

max

=23.21%

609

Рассмотрим модель ГПП с учетом развития трещин в ЗВС нагнета-

тельной скважины для условий (табл. 6.7) и динамики приемистости

на рис. 6.45 –

в. Показанная на рис. 6.49–6.50 динамика развития тре-

щины в ЗВС нагнетательной скважины отражает постепенное развитие

трещины в направлении осей

X и Y в среднем слое – l = 5. Так как ва-

риация проницаемости составляет 50% (от средней 18.5 мД) – 16.5–

20.5 мД согласно нормальному распределению, то трещина описыва-

ется неоднородной сетью трещин, которая по мере работы скважины

стремится стать однородной, что связано с невысоким значением про-

ницаемости трещин –

тр

=50000 мД. Вследствие того, что градиент

разрыва выбран небольшим – 0.1 МПа/м сеть трещин достаточно раз-

вита. При больших градиентах разрыва сеть трещин более компактна и

сформирована меньшим количеством, но крупных трещин. Последнее

будет показано далее. При использовании модели ГПП с учетом тре-

щинообразования следует иметь в виду, что приращение времени –

Δt

должно выбираться более малым, чем без учета трещин, так как дис-

кретное падение гидравлического сопротивления ячеек может привес-

ти к чрезмерному «биению» расчетных величин.

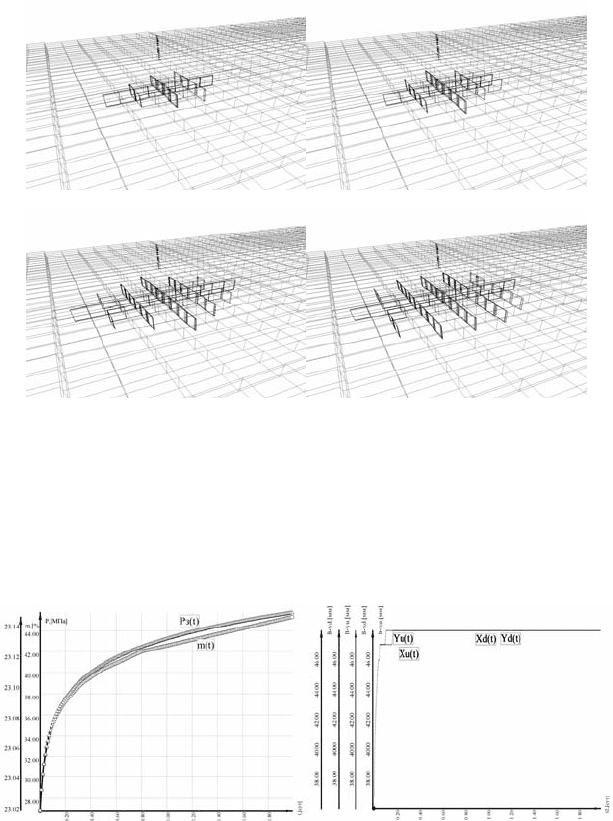
0.01 сут 0.05 сут

0.07 сут 0.09 сут

Рис. 6.49. Динамика распространения трещины в нагнетательной скважине

с динамикой приемистости (см. рис. 6.45–

в), ЗВС в сечении

610

0.16 сут 0.37 сут

0.72 сут 1.31 сут

Рис. 6.50. Динамика распространения трещины в нагнетательной скважине

с динамикой приемистости (см. рис. 6.45 –

в), ЗВС в сечении

Естественно, неоднородность прочностных свойств пласта здесь не

учитывается. На рис. 6.51 –

а показана зависимость забойного давле-

ния и открытой пористости в нагнетательной скважине от времени. На

рис. 6.52 –

б показаны графики зависимости толщины трещин в ПЗП

нагнетательной скважины от времени в четырех направлениях. Дан-

ные графики отражают постепенное раскрытие трещин в ПЗП.

а) б)

Рис. 6.51. Динамика ФЭС в окрестности 40 м от забоя нагнетательной

скважины:

а – забойного давления и открытой пористости; б – толщин

трещин в направлениях против – «d» и вдоль – «u» осей

X и Y