Стрекалов А.В. Математические модели гидравлических систем для управления системами поддержания пластового давления
Подождите немного. Документ загружается.

631
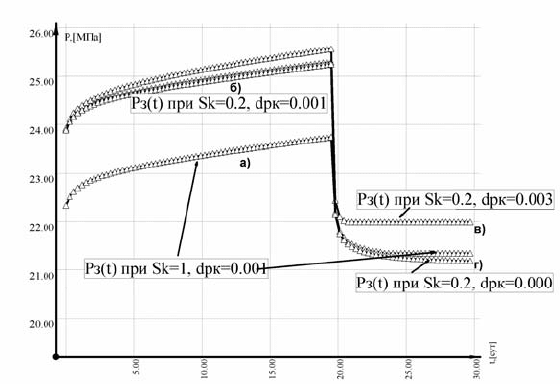
Рис. 6.80. Динамика забойного давления в нагнетательной скважине с
отработкой в течение 20 сут и остановка с выдержкой в течение 20 сут
(здесь dpk=
н,в
к
dp
, Sk=S
k
)
Как видно из рис. 6.80 – в, наибольший рост и скорость падения
давления соответствует градиенту сдвига – 0.003, так как при этом
больш
ая часть жидкости в ЗВС остается неподвижной и препятствует
нагнетанию. Для кривой на рис. 6.80 –
г характерно длительное паде-
ние давления в связи с тем, что вся жидкость в ЗВС подвижна. Наи-
меньший рост давления и немного более длительное по сравнению
(
S
k
= 0.003) падение давления характерно для кривой на рис. 6.80 – а,
так как проницаемость в ПЗП одинакова с проницаемостью остальной
части ЗВС.
Рассмотрим результаты вычислительного эксперимента для иссле-
дования динамики давления в нагнетательной скважине 407Р, вскры-
вающей пласты А1(3), А1(1–2) и А2(1) с проницаемостями 215, 16 и
55 мД и начальными пластовыми давлениями 16.36, 16.05 и 16.47 МПа
соответственно. Нагнетательную скважину запустим с приемистостью
1500 т/сут и вык
лючим через 50 сут. Деформационные свойства
пластов примем одинаковыми. На рис. 6.81 показано распределение
давления в ПЗП данной скважины до и после остановки. Следует от-
метить, что в данной модели ГПП пласты считались гидравлически ра-
зобщенными по вертикали. Вследствие этого распределение давления
632
пластов различно. На рис. 6.82 показана динамика забойного давления
в скважине и пластового давления на расстоянии 18 м от забоя для
каждого из пластов.
а) б)
Рис. 6.81. Модель ГПП в разрезе пластов в точке забоя нагнетательной
скважины по вертикали вдоль оси
X (заливка по давлению
P
min
=16.05 МПа, P
max
=29.6 МПа): а – время 49.75 сут; б – время 50.25 сут
(т.е. после остановки)
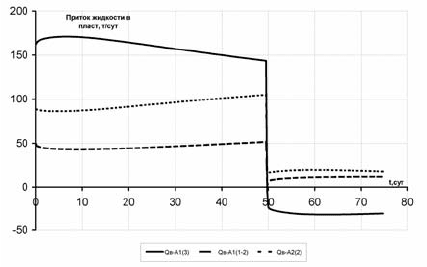
Из графиков динамики пластового давления на рис. 6.82 видно, что
при закачке воды давление больше всего растет в пласте с наиболь-
шей проницаемость – А1(3), так как и объем закачиваемой воды в не-
го тоже наибольший (см. рис. 6.83). После отключения скважины воз-
никают межпластовые перетоки: пласт А1(3) дренируется пластами
А1(1–2) и А2(1), причем, п
оследний принимает жидкость больше, так
как имеет большую
проницаемость. Судя
по динамике прито-
ков и давлений,
окончательное урав-
нивание давлений не
предвидится в бли-
жайшие 50–100 сут.
Это свидетельствует
о том, что в много-
пластовых скважи-
нах без изоляции
пластов проводить
ГДИ посредством
снятия КВД/КПД не только неэффективно, но и бесполезно.
Рис. 6.82. Динамика забойного и пластовых дав-
лений в модели ГПП
633
Одной из основных особенностей предлагаемой модели ГПП явля-
ется специфика хранения данных, описывающих расчетные и исход-
ные свойства элементов ГПП (ячеек). В динамической памяти расчет-
ного модуля – root находится только пять рядов ячеек по оси
X: один
основной ряд, а четыре остальных со сдвигом основного ряда по осям
Y и Z на индекс вперед и назад для расчета перетока между ячейками,
трещин и ФЭС.
Таким образом, требуемая для расчета модели ГПП динамическая
память, исполь-
зуемая для рас-
чета ФЭС и пе-
ретоков между
ячейками, равна
произведению
объема инфор-
мации по одной
ячейке (52 байт)
на количество
ячеек по
X (nx) и
рядов (5) –
V
I
=
=52
×nx×5. Т.е.
фактически ко-
личество ячеек и
степень детали-
зации процессов в предлагаемой модели ГПП не ограничивается воз-
можностями ЭВМ. Все данные о свойствах ячеек модели располагают-
ся на постоянном носителе (Hard Disk Drive), а помере вычислений
они считываются и сохраняются. Конечно, для малого количества яче-
ек до 1 млн. такая схема является неоптимальной, однако, пр
и росте
количества ячеек более 10–20 млн. такая схема обработки информации
становится единственно возможной для ПК. В частности, для аналогов
таких моделей (Eclipse, Техсхема, Tempest) количество ячеек ограни-
чено доступной динамической памятью, что несколько ограничивает
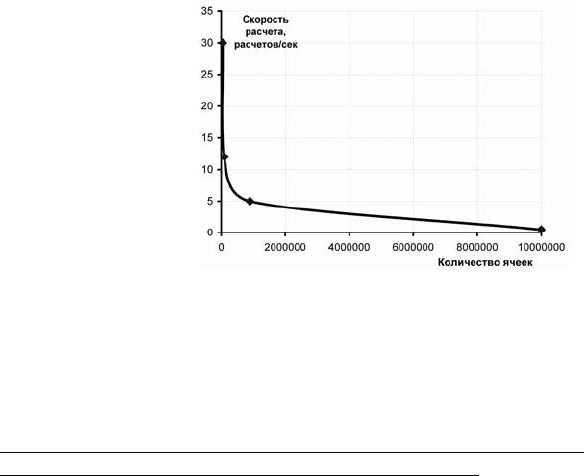
область их применения на ПК. На рис. 6.84 показана зависимость ско-
рости расчета предлагаемой модели ГПП от количества ячеек.
Дл
я получения результатов вычислений модели ГПП на рис. 6.60–
6.66 при
Δt = 0.007 сут и расчете прогноза на 910 сут количество рас-
четов составило 130000 и заняло на ПК–AMD3200+ с объемом дина-
мической памяти 512 Mбайт – 1 ч 22 мин при
nx = 100, ny = 100,
Ls = 10. Естественно, для получения лучших результатов скорости вы-
Рис. 6.83. Динамика притоков жидкости по пластам в
первом слое (количество слоев равно 5, поэтому
суммарный приток по пласту равен произведению
притока в первом слое на 5)
634
числений предлагаемой модели ГПП и аналогов необходимо исполь-
зовать не персональные компьютеры, а ЭВМ типа MainFrame, микро-
и мини- ЭВМ, что вполне обосновано, когда речь идет о больших эко-
номических затратах на разработку и эксплуатацию месторождений,
не говоря уже о возможных потерях, возникающих при недостаточно
точном прогнозировании. В настоящее время возникла ст
ранная си-
туация с использованием моделей ГПП, состоящая в том, что с целью
ускорения расчета или достижения выполнения расчетных прогнозов
на ПК за приемлемое время количество ячеек модели сокращается
(«upscaling»), что негативно отражается на точности вычислений и де-
тализации моделируемых процессов. В частности, при формировании
моделей ГПП
месторождений За-
падной Сибири ли-
не
йные размеры ячеек
по осям
X и Y могут
достигать 100–500 м,
что, естественно, не
может быть адекват-
ным, особенно, если
вспомнить какого ро-
да допущения прини-
маются при расчете
ФЭС в ячейках. Наи-
более адекватными
размерами ячеек вне
зависимости от разме-
ров пластов являются размеры от 1 до 50 м. Что касается ячеек-
стволов скважин, то их размеры должны быть еще меньш
е: локальное
измельчение.
6.5. Пример использования модели гидросистем продуктивных
пластов совместно с моделью технических гидросистем
Вследствие того, что в качестве граничных условий для скважин
задаются зависимости притока/оттока жидкости или компонентов от
времени
Q(t) вне зависимости от состояния наземной части гидросис-
темы ППД динамику расчетных показателей элементов модели ГПП
нельзя полностью считать достоверной. Так как при изменении давле-
ния на забое скважин вследствие изменения состояния ГПП будут из-
меняться величины оттока или притока, то использование МТГС со-
Рис. 6.84. Зависимость скорости расчета
модели ГПП на один момент времени от
количества ячеек
635
вместно с моделью ГПП может более точно отразить такого рода из-
менения с учетом динамики ФЭС элементов модели ГПП и гидравли-
ческих параметров звеньев и структуры МТГС.
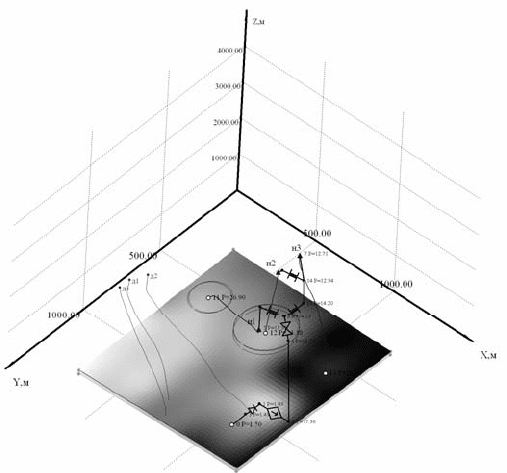
Рассмотрим пример модели на рис. 4.85. Как видно из схемы,
МТГС представлена тремя нагнетательными (обозначены прификсом
«н») и тремя добывающими скважинами (прификс – «д»), сетью тр
у-
бопроводов и КНС, а модель ГПП представлена тремя пластами –
А1(1), А1(2–3) и А4. Причем, каждая добывающая скважина вскрывает
все три пласта, а нагнетательные избирательно: скважина «н1» – пла-
сты А1(1) и А1(2–3), «н2» – все пласты, а «н3» – А1(1) и А4.
Рис. 6.85. Схема совместной модели ГПП и МТГС (видимый пласт А(1),
заливка по абсолютной проницаемости k
min
= 38.16, k
max
= 178.75 мД)
Начальную нефтенасыщенность примем равной 35% по всем пла-
стам, пластовое давление к моменту пуска нагнетательных и добы-
вающих скважин будет равномерным: А1(1) – 16.27, А1(2–3) –16.54,
А4 – 17.41 МПа. Размеры пластов по
Х и Y равны 1000 м. Средняя
толщина А1(1) – 6.47 м, А1(2–3) – 14.84 м, А4 – 43.03 м. Средние про-
ницаемости пласта А1(1) – 108 мД, А1(2–3) – 37 мД , А4 – 159 мД.
Прочие параметры модели соответствуют табл. 6.9, за исключением

636
проницаемости трещин (здесь она равна 50 Д) и учета нарушения за-
кона Дарси (здесь он учитывается). Добывающие скважины опишем
постоянным отбором жидкости: «д1» – 500 т/сут, «д2» – 300 т/сут,
«д3» – 400 т/сут.
Исследуем динамику ФЭС в течение времени от 0 до 9 сут. На рис.
6.86–6.88 показано распределение давления в ячейках пластов средне-
го сл
оя на отрезке времени 0.04–0.9 сут.
а) б)
Рис. 6.86. Заливка по давлению пласт А1(1):
а – 0.04 сут, P
min
=15.99,
P
max
=17.89 МПа; б – 0.9 сут, P
min
=15.36, P
max
=20.49 МПа;
а) б)
Рис. 6.87. Заливка по давлению пласт А1(2–3):
а – 0.04 сут, P
min
=16.14 ,
P
max
=19.45 МПа; б – 0.9 сут, P
min
=15.67, P
max
=21.15 МПа
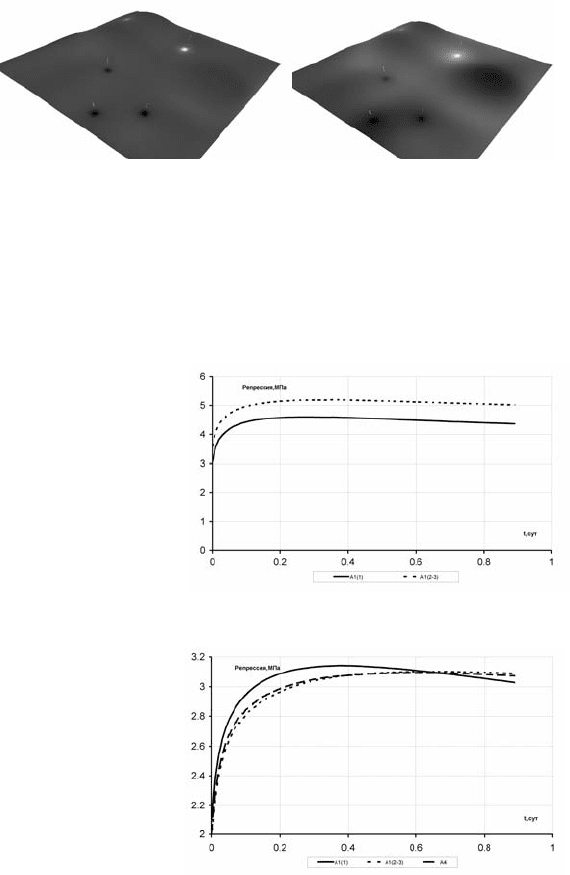
Как видно из рис. 6.88, давление в ЗВС нагнетательных скважин
пласта А4 растет медленнее, чем в остальных пластах. Это связано с
тем, что данный пласт имеет толщину выше остальных примерно в 3–
3.5 раза. Форма пластов взята с достаточно большими колебаниями аб-
солютных отметок кровли и подошвы пластов, поэтому наличие зон с
большими значениями АО обу
славливает тенденции к формированию
пластового давления в ЗВС нагнетательных скважин (см. рис. 6.86 –
б,
рис. 6.88 –
б).
637
а) б)
Рис. 6.88. Заливка по давлению пласт А4:
а – 0.04 сут, P
min
=16.92 ,
P
max
= 18.68 МПа; б – 0.9 сут, P
min
= 16.44 МПа, P
max
=19.56 МПа
Динамику ФЭС в модели ГПП детально рассматривать не будем,
так как основные факторы были показаны выше на подобных моделях
в отдельности от МТГС. Рассмотрим наиболее интересные факторы
взаимодействия ГПП и ТГС в виде динамики гидропараметров ТГС.
На рис. 6.92–6.94
показана динамика
приемистостей нагне-
тательных скважин по
пластам, а на рис.
6.89–6.91 показана ди-
на
мика репрессии, соз-
даваемой нагнетатель-
ными скважинами на
заводняемые пласты.
Из графиков данных
зависимостей видно,
что с течением време-
ни режимы работы
пластов не устанавли-
ваются. Это характе-
ризует данную ГПП
как инерционную, а
следовательно, данная
система будет прак-
тически не исследуе-
ма ГДИ на устано-
вившихся режимах
отбора или за
качки.
Рис. 6.89. Динамика репрессии пластов нагнета-
тельной скважины – «н1»
Рис. 6.90. Динамика репрессии пластов нагнета-
тельной скважины – «н2»
638
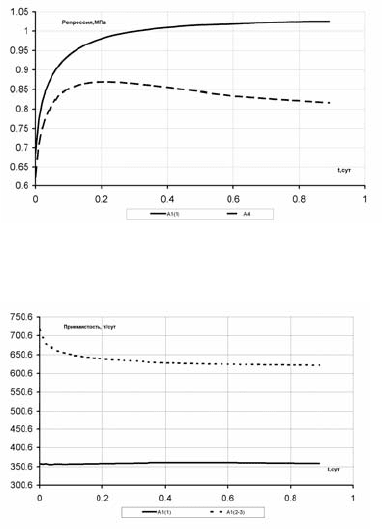
Графики зависимости репрессии от времени отражают неустойчи-
вый характер формирования пластового давления на контуре ЗВС, т.е.
сначала репрессии быстро растут, а затем начинают падать. Такого ро-
да зависимости отра-
жают изменение ком-
плексного потокорас-
пределения в наземной
части системы ППД,
которая вследствие
взаимодействия эле-
ментов ТГС реагирует
изменением всех ги
д-
ропараметров на изме-
нение состояния ГПП.
Аналогичная кар-
тина наблюдается и с
динамикой приеми-
стостей, которая от-
ражает как рост, так и
падение ее значений с
течением времени
(рис. 6.92 – 6.93).
По большей части
характер реакции на-
земной ТГС обуслав-
ливается гидравличе-
ской характеристикой
КНС и, составляющих
ее АСГ. Так как ха-
р
актеристика применяемых в системах ППД насосов АСГ
СТР
(типа
ЦНС) является «мягкой», режимы работы ТГС в целом также отража-
ют «мягкую» взаимосвязь давлений и расходов жидкости в элементах
системы (см. рис. 6.95).
В дополнение к этому, если исследовать характер взаимодействия
сети трубопроводов, скважин и УУ с насосными агрегатами, то стано-
вится ясным, что при наложении их характеристик вид регулировоч-
ных кривых становится еще менее предсказуемым, не говоря уже о ха-
рактере взаимодействия с ГПП.
Рис. 6.91. Динамика репрессии пластов нагнета-
тельной скважины – «н3»
Рис. 6.92. Динамика приемистости пластов на-
гнетательной скважины – «н1»
639
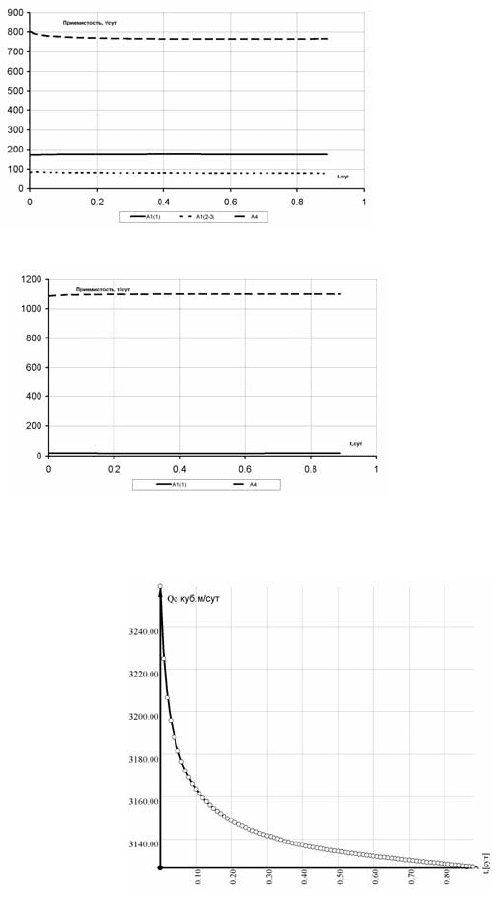
Рис. 6.93. Динамика приемистости пластов нагнета-
тельной скважины – «н2»
Рис. 6.94. Динамика приемистости пластов нагнета-
тельной скважины – н3
В рассмотренной со-
вместной модели учиты-
вались все описанные
факторы: трещинообра-
зование, нарушение за-
кона Дарси, изменение
открытой пористости и
проницаемости от давле-
ния. На данный момент
детально выявить сте-
пень влияния каждого из
этих факторов на харак-
тер взаимодействия ТГС
и ГПП не представляется
возможным. Поэтому для
повышения точности мо-
Рис. 6.95. Динамика режима АСГ
640
делирования необходимо использовать предложенные модели ТГС и
ГПП совместно.
Что касается динамической оптимизации ТГС с учетом изменения
состоянии ГПП, то судя по требуемым вычислительным ресурсам, она
потребует у современных ЭВМ недопустимо большое время для рас-
чета прогнозирования. Поэтому эффективное решение такой задачи
пока не предвидится. С точки зрения практического использования
МТГС при планировании мероприятий по регулированию и оптимиза-
ции для те
кущих условий эксплуатации ГПП (например, в течение 1–2
лет), вполне подходят описанные методы контроля и управления с ис-
пользованием МТГС отдельно от модели ГПП.
Исследование модели взаимодействия ГПП и ТГС в течение дли-
тельного времени в текущих условиях развития отрасли видится пока в
исключительно теоретических изысканиях, направленных на развитие
моделей гидросистем.
Тем не мен
ее, проводя вычислительные эксперименты на модели
ТГС+ГПП на сравнительно короткий срок (не более 1– 6 мес.), можно
выявить характер техногенного воздействия на ГПП со стороны ТГС и
разработать мероприятия по оптимизации ТГС для повышения эффек-
тивности заводнения.
