Стрекалов А.В. Математические модели гидравлических систем для управления системами поддержания пластового давления

Подождите немного. Документ загружается.

451

водилась раздельно, т.е. при возвращении к базовому набору варьиро-

вался следующий параметр.

Что касается первого вида погрешностей, то здесь следует отме-

тить, что они являются наиболее весомыми и, к сожалению не устра-

нимыми посредством коррекции математического описания самой мо-

дели ГПП. Второй вид погрешностей, с точки зрения анализа качества

моделей ГПП, на

иболее интересен, так как посредством настройки

размеров ячеек и величины приращения времени можно настроить

модель на наиболее точное решение. На рис. 4.140 показаны примеры

зависимостей

()

(

)

(

)

И,V,t

, где

– относительный объем яче-

ек, равный отношению объема ячеек к объему пласта, И – интервал

случайной вариации ФЭС в % от базовых величин.

Принятые базовые параметры модели: Δt

= 10 сут, V

= 60×45×2 м

=1⋅10

–5

, объем пласта 540 000 000 м

. Разумеется, вид функций на

рис. 4.140 будет отличаться для различных наборов базовых ФЭС, по-

ложения и режимов работы скважин (они не варьировались). Однако,

они отражают общий характер взаимосвязи результатов расчета с па-

раметрами и факторами модели. По-видимому, такого рода зависимо-

сти будут наблюдаться для большинства моделей ГПП, основанных на

конечно-разностном выр

ажении элементов пласта (в виде ячеек). В

частности, подобные зависимости наблюдаются и для предлагаемой

здесь модели ГПП.

Размеры ячеек для всех моделей, построенных на основании заме-

ны бесконечно-малых приращений конечными величинами, являются

основным источником погрешности, так как все допущения связаны

именно с тем, что размеры ячеек должны быть весьма малыми. Одна-

ко, при уменьшении размеров ячеек, во-первых, резко растет нагрузка

на ЭВМ (зависимость третьей степени), а во-вт

орых, необходимо, рез-

ко снижать параметр Δt, так как за большее время приток или отток из

ячейки может не обеспечиваться объемом ячейки и содержащихся в

ней флюидов. Например, если размеры ячейки составляют

100×100×1 м, то Δt при максимальном притоке/оттоке J=1000 кг/сут

можно принять порядка нескольких су

ток, а при размерах 10×10×1 м

Δt может быть не более 2–4 ч. Таким образом, размеры ячеек и прира-

щение времени являются связанными параметрами, а зависимость на-

грузки на ЭВМ от средних размеров ячеек по осям будет близка к

функции шестой степени (например

⋅

, где L – средний размер

ячейки, а

А – некоторый коэффициент). Во избежание большой на-

452

грузки на ЭВМ в большинстве моделей используются различные

приемы (хитрости), скрывающие погрешности моделирования. К та-

ким приемам относятся:

−

разбиение базовых ячеек на более мелкие там, где происходит

интенсивный приток/отток (в основном, в районе скважин);

−

при обнаружении невозможности соблюдения материального

баланса при перетоках между ячейками приращение времени

делится до тех пор, пока материальный баланс (масса находя-

щихся в ячейке флюидов –

M достаточна для обеспечения

полученного оттока) или закон сохранения энергии (деформа-

ция породы и компонентов соответствует положительной вели-

чине давления) может быть соблюден.

Первый прием достаточно эффективен и не приводит к серьезному

наращиванию погрешности при допустимом приращении времени.

Однако, вследствие измельчения ячеек в районе скважин требуется

соответствующее уменьшение приращения времени так, чтобы соблю-

дался мат

ериальный баланс, причем, с некоторым запасом (т.е. непре-

дельным истощением ячейки или расширением порового пространства

до

...

объема ячейки). Что же касается второго приема, то здесь

можно с уверенностью сказать о неприемлемости такого подхода. До-

пустим, ячейка i, в которой рассчитан суммарный приток воды –

∑

m =1000 кг/сут, имеет размеры V

=10×10×1 м, а приращение вре-

мени Δt =1 сут, тогда, очевидно, энергетический баланс не может быть

обеспечен: грубо говоря, такая масса –

J =

∑

m ⋅Δt в ячейку «не

влезет». Тогда согласно второму приему величина Δt будет умень-

шаться делением на некоторую постоянную (чаще всего пополам) до

тех пор, пока

J <B⋅V (где B – некоторый коэффициент). Выполнение

материального баланса может быть проверено для условий оттока из

ячейки:

J <

MM − , где

M – остаточные запасы компонента

Ф в ячейке i

. Естественно, что соблюдение данных условий будет при

максимально возможной величине Δt. Очевидно, что такой прием мо-

жет привести к существенным погрешностям вследствие того, что па-

раметр Δt, во-первых, адаптируется к ячейкам с наибольшим притоком

и оттоком, а во-вторых, обуславливает неравномерное приращение

453

времени при расчете неустановившегося потокораспределения в

пласте. Последенее делает потокораспределение между ячейками мо-

дели ГПП не равноценным по точности для различных отметок време-

ни. По мнению автора, параметр Δt должен устанавливаться до начала

расчета в зависимости от потенциальных перетоков между ячейками,

их объемов, сжимаемостей и пористостей для всей модели ГПП на

весь п

ериод расчетного времени. Это хотя бы позволит контролиро-

вать и управлять точностью расчета. Ниже этот вопрос будет рассмот-

рен более подробно.

Модель внутрипластовой фильтрации нефти и воды

для использования совместно с моделью технических

гидросистем поддержания пластового давления

Предлагаемая здесь модель ГПП представляет собой математико-

численную модель, реализованную в ПРК Hydra’Sym. Основной пред-

посылкой к описанию данной модели является известный в моделиро-

вании подход: структурное разделение гидросистемы продуктивных и

заводняемых пластов на конечные элементы прямоугольной формы –

ячейки. Визуально модель ГПП, состоящая из С пластов, каждый из

которых разбит по вертикали на Ls сл

оев, по горизонтали вдоль оси X

на nx, а вдоль оси Y на ny ячеек равных размеров, выглядит аналогично

рис. 4.141. Ячейки будем индексировать следующим образом: c=0..C–1

– номер пласта, l=0..Ls–1 – номер слоя, k=0..ny–1 – номер по оси Y,

j=0..nx–1 – номер по оси X.

Как ви

дно из схемы на рис. 4.141, размеры ячеек в плоскости X–Y

одинаковы для всей модели:

minmax

−

minmax

−

Размеры ячеек по вертикали неодинаковы вследствие изменения

толщины пласта и определяются из интерполирующих поверхностей

кровли и подошвы пласта с индексом c:

(4.250)

454

[]

[] []

[]

[] []

⎥

⎦

⎤

⎢

⎣

⎡

+⋅++⋅+−

−+⋅+⋅+−

−⋅++⋅+−

−⋅+⋅+−

−+⋅++⋅++

++⋅+⋅+

+⋅++⋅++

+⋅+⋅+

⋅

)kLY,jLX(f

XminXminп

XminXminк

j,k,l,c,Z

где

– функция, интерполирующая абсолютные отметки кровли

пласта – c;

– функция, интерполирующая абсолютные отметки по-

дошвы пласта c.

Глобальный индекс ячейки определяется следующим образом:

nxnyc

snxnyi

⋅

+⋅

⋅

где

1..0

−

⋅

⋅= CLsnynxi

Далее под индексом i будем полагать его расшифровку (4.252).

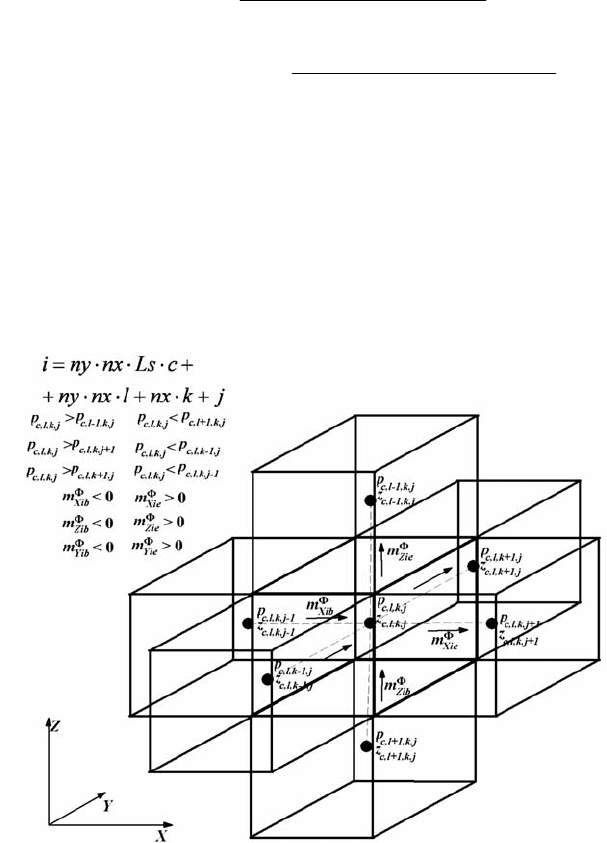
Структурная взаимосвязь ячеек определяется индексацией, т.е. ячейка

(c, l, k, j) структурно связана (т.е. возможен переток) с ячейками этого

же пласта (c, l, k, j+1), (c, l, k, j–1), (c, l, k+1, j), (c, l, k–1, j), (c, l+1, k, j),

(c, l–1, k, j). Если ячейка находится на верхней (c, l=0, k, j) или нижней

(c, l=Ls–1, k, j) границе пласта, то она также может быть связана с

ячейками смежного пласта сверху (если таковой есть) – (c–1, l=Ls–1,

k, j) или снизу – (c+1, l=0, k, j) (рис. 4.142).

Геометрическое положение ячеек по вер

тикали определяется вели-

чиной z

, соответствующей абсолютной отметке (высоте над уровнем

моря) центра ее фигуры, и определяется согласно интерполирующей

кровлю функции –

f и длине ячейки по оси Z (высота ячейки):

[]

[] []

j,k,l,c,Z

XminXminк

)j,k,l,c(i

)kLY,jLX(f

⋅−

⎥

⎦

⎤

⎢

⎣

⎡

+⋅++⋅++

++⋅+⋅+

+⋅++⋅++

+⋅+⋅+

(4.251)

(4.252)

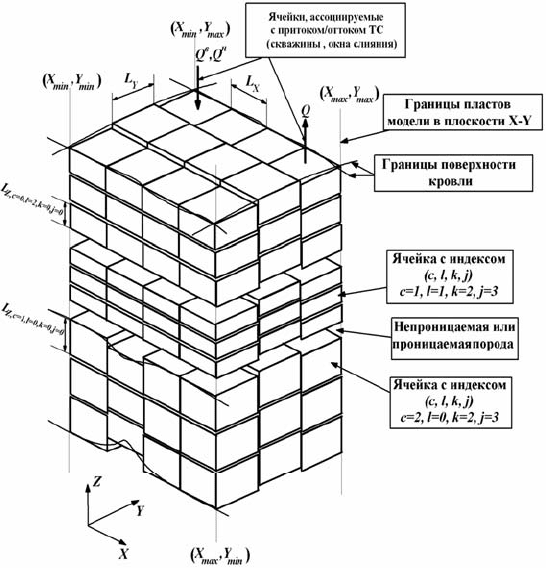
455

Рис. 4.141. Визуальное представление модели ГПП, состоящей из трех пла-

стов, разбитых по вертикали на 4 слоя, по оси X на 4 ячеек, по оси Y на

3 ячейки

На рис. 4.141 (сверху) показаны ячейки, ассоциированные со сква-

жинами или окнами слияния, через которые осуществляется приток

или отток компонентов во внешнюю ГС. Для таких ячеек динамику

притока/оттока будем описывать зависимостями массового расхода от

времени:

()

для воды и

(

)

для нефти. Эти функции будут од-

ними из основных граничных условий.

Начальными условиями для времени t = 0 (до техногенного воздей-

ствия на ГПП) являются величины пластовых давлений в ячейках –

i,t

, абсолютные проницаемости в ячейках по координатным осям

456

–

)X(

i,t

, ,k

)Y(

i,t 0=

)Z(

i,t

, открытые пористости в ячейках

отк

i,t

и на-

сыщенности компонентов в ячейках

i,t

. Данные факторы

определяются из интерполирующих функций, соответствующих опи-

сываемому параметру аналогично (4.251). Например, для определения

абсолютной проницаемости вдоль оси X пласта c слоя l в ячейке i:

[]

[] []

⎥

⎦

⎤

⎢

⎣

⎡

+⋅++⋅++

++⋅+⋅+

+⋅++⋅++

+⋅+⋅+

⋅

)kLY,jLX(f

XminXmink

)X(

)j,k,l,c(i,t

где

– функция, интерполирующая абсолютную проницаемость

пласта c в слое l вдоль оси X. Обычно проницаемости по осям X и Y

принимаются одинаковыми.

Для описания динамики свойств ГПП в ячейках необходимо опи-

сать множество T точек времени, соответствующих последовательно-

му приращению Δt. Элементами множества будут точки времени [t

, t

,…,t

] такие, что

ttt

где I – индекс, соответствующий номеру расчета установившегося по-

токораспределения в течение времени Δt.

Для описания, установившегося в течение времени Δt потокорас-

пределения при известных на данный момент давлениях в ячейках не-

обходимо определить величины притоков/оттоков во всех ячейках.

Для этого согласно зависимостям

)p(

Si,Ф

следует определить вели-

чины массовых расходов компонентов истекающих (или притекаю-

щих) из ячейки. На рис. 4.142 отображена схема определения массо-

вых расходов в ячейке i(c,l,k,j) относительно прилегающих к ней ячеек.

Для вычисления массового расхода, истекающего с грани U по оси

S ячейки i компонента Ф, необходимо решить нелинейное уравнение

относительно неизвестного давле

ния на грани между ячейками –

SiU

. Например, для фильтрации вдоль оси Х должно выполняться

равенство массовых расходов компонентов, истекающих из ячейки

(c,l,k,j) и притекающих в смежную ячейку (c,l,k,j+U):

(4.253)

(4.254)

457

(

)

()

zzg)p(

j,k,l,cUj,k,l,cUj,k,l,cФ

Uj,k,l,cXiU

)Uj,k,l,c(X,Ф

Uj,k,l,c

Uj,k,l,cj,k,l,cj,k,l,cФ

XiUj,k,l,c

)j,k,l,c(X,Ф

j,k,l,c

⎟

⎠

⎞

⎜

⎝

⎛

−

+−=

⎟

⎠

⎞

⎜

⎝

⎛

−

+−

где

)j,k,l,c(X,Ф

j,k,l,c

– замыкающее отношение: зависимость массового

расхода компонента Ф ячейки (c, l, k, j) при фильтрации вдоль

оси X;

)Uj,k,l,c(X,Ф

Uj,k,l,c

– замыкающее отношение: зависимость массово-

го расхода компонента Ф смежной по грани U ячейки (c,l,k,j+U)

при фильтрации вдоль оси X;

U – инкремент, отражающий смещение индекса ячейки и может

принимать значения +1 и –1 в зависимости от рассматриваемой

по оси смежной ячейки (для оси Х слева –1, а справа +1).

Рис. 4.142. Пример определения массовых расходов компонента Ф

в ячейке i

(4.255)

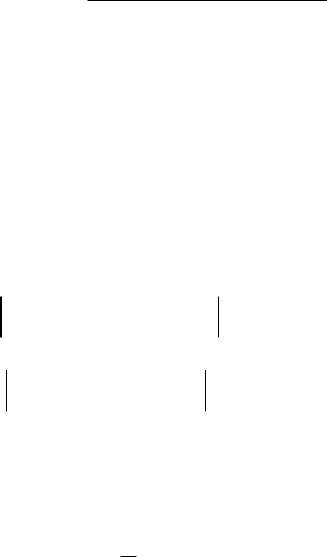
458

Уравнение (4.255) можно решить численным методом Ньютона или

методом «хорд». Наиболее подходящим для решения (4.255) является

метод «адаптивной линеаризации» (см. раздел 4.4). Получив из реше-

ния (4.255) неизвестное давление на грани

XiU

, находим массовый

расход компонента через грань XiU

()

⎟

⎠

⎞

⎜

⎝

⎛

−

+−=

Uj,k,l,cj,k,l,cj,k,l,cФ

XiUj,k,l,c

)j,k,l,c(X,Ф

j,k,l,c

XiU

zzg)p(

ppm

Особенно важно отметить следующее условие решения (4.255). Де-

ло в том, что характер насыщения смежных ячеек при определенных

условиях может быть таким, что величина относительной проницаемо-

сти по одному из компонентов равна нулю в одной ячейке, а в смеж-

ной с ней может быть отличной от нуля. В этом случае решение (4.255)

приводит не

известное давление

XiU

p к равному давлению в одной из

ячеек (например, если относительная проницаемость компонента Ф в

ячейке (c,l,k,l+U) равна нулю, то

j,k,l,cXiU

), поэтому перед ре-

шением этого уравнения необходимо убедиться, что выполняются ус-

ловия:

0>Δ

)p(

Xк

)Uj,k,l,c(X,Ф

Uj,k,l,c

0>Δ )p(

Xк

)j,k,l,c(X,Ф

j,k,l,c

где

Xк

pΔ

– некоторый минимальный перепад давления, при котором

возможна фильтрация компонента Ф вдоль оси Х, равный произведе-

нию градиента давления начала фильтрации на половину длины ячей-

ки вдоль оси S:

Sк

Ldpp

=Δ

В частности, величина

Sк

в работе [182] названа начальным

градиентом давления.

Sк

dp будем называть градиентом сдвига

компонента. Таким образом, если условие фильтрации не выполняется

хотя бы в одной из смежных ячеек, то следует считать отсутствие пе-

ретока между ячейками, т.е. для примера (4.256)

XiU

= 0 для соот-

(4.256)

459

ветствующей грани – U и смежных с этой гранью ячеек. Даже если

полагать присутствие компонента в обеих ячейках, то при текущем

перепаде давления по оси S , если

Sк

Ldpp

<Δ

, фильтрация про-

исходить не будет:

(

)

0=Δ

S,Ф

. Соблюдение такого условия необ-

ходимо также для учета реологических свойств компонентов [200].

Можно предусмотреть приближенный способ определения перето-

ка масс компонентов между ячейками, если течение соответствует ли-

нейному виду замыкающих отношений

)( p

: 1 – с учетом сложения

сопротивлений фильтрации по каждой из пары ячеек и компоненту –

зависимая проводимость; 2 – без учета сложения сопротивлений

фильтрации по каждой ячейке –

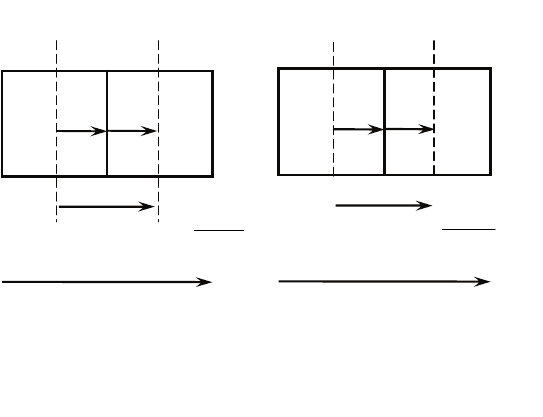
независимая проводимость. На рис.

4.142/1– а и б показана схема расчета массового перетока компонента

– Ф.

Для зависимой проводимости, если

, то

⎥

⎦

⎤

⎢

⎣

⎡

⋅

⋅≈∞=

кг

сПа

101

)Ф,S(

, и если

, то

⎥

⎦

⎤

⎢

⎣

⎡

⋅

⋅≈∞=

кг

сПа

101

)Ф,S(

отсюда

1221

−−

. При этом, если не выполняются условия

выше, то сопротивления ячеек складываются при определении сум-

марного сопротивления, из которого и перепада давления определяет-

ся массовый расход между ячейками через соответствующую грань:

)Ф,S()Ф,S(

1221

−

=−=

−−

Для независимой проводимости выбор сопротивления зависит от

того, в какой из пары ячеек давление выше. Если

PP >

, то

)Ф,S(

1221

−

=−=

−−

а если

PP <

, то

)Ф,S(

1221

−

=−=

−−

Также, если

PP >

, то

1221

−−

и если

, то

1221

−−

460

Для схемы на рис. 4.142/1 – а при нулевой фазовой проницаемости

любой из пары ячеек фильтрация считается нулевой, а для схемы на

рис. 4.142/1 – б фильтрация невозможна только тогда, когда в ячейке с

наибольшим давлением фазовая проницаемость равна нулю, при этом

проводимость половины второй ячейки считается равной проводимо-

сти половины первой.

Такие соп

особы определения перетока между ячейками подходят

для условия соблюдения линейного закона фильтрации.

Если

XiU

>0, то отток из ячейки (c,l,k,j) и приток в ячейку

(c,l,k,j+U). Аналогичным образом определяются расходы по осталь-

ным направлениям и граням рассматриваемой ячейки.

Так как модель ГПП ограничена по вертикали и горизонтали, то

при отсутствии смежной ячейки массовый расход не вычисляется для

соответствующих граней. Это касается ячеек границ пласта: j = nx–1,

k = ny–1

и l = Ls–1.

После определения всех массовых расходов, соответствующих те-

кущему потокораспределению – I, вычисляются давления через опи-

санные ранее функции изменения давления и открытой пористости

при притоке/оттоке из ячеек:

(

)

(

)

[

]

IIIIIII

itI

itiitit

pMMtQJtQJpp ,,,,

,,,,,,

+++=

;

)Ф,S(

)Ф,S()Ф,S(

rrr

)Ф,S(

1221

−

=−=

−−

)Ф,S(

)Ф,S()Ф,S(

rrrr

)Ф,S()Ф,S(

или , ==

)Ф,S(

1221

−

=−=

−−

а) б)

Рис. 4.142/1. Схема приближенного расчета перетока между

ячейками i=1, i=2: а – зависимая проводимость; б – независимая

проводимость

(4.257)