Стрекалов А.В. Математические модели гидравлических систем для управления системами поддержания пластового давления

Подождите немного. Документ загружается.

421

где

– количество слоев для распределения ФЭС по объему;

– количество величин ФЭС;

пл

– количество пластов в ГПП.

Тогда объем информации, необходимый для хранения и использо-

вания геологической модели, будет определяться зависимостью

(

)

valueYXплФLvalueYXповI

VGGnnnVGGNV

⋅

⋅⋅⋅= 323

где V

– объем информации, байт;

– количество точек сетки по Х;

– количество точек сетки по Y;

value

– количество байт для хранения одного числа (4, 8 или 10).

Причем, множитель 3 означает хранение трех координат, что необ-

ходимо для геологических моделей, пласты которых имеют разные

границы области определения X–Y. Если границы одинаковы, тогда

сомножитель 3 можно исключить. Если

500

, то

()

21600000008350050052710 =⋅⋅⋅⋅⋅+⋅=

Байт=2059.9 Мбайт.

Из приведенного расчета следует, что использование сетки 500×500

практически невозможно, так как работа ЭВМ с таким объемом ин-

формации будет недопустимо медленной. Поэтому наиболее часто

используемой сеткой является 100×100, а объем информации для на-

шего примера составляет

()

3982864000008310010052710 .V

⋅

⋅+⋅=

Мбайт.

Такой объем информации вполне приемлем для обработки и хране-

ния на ЭВМ широкого спектра. Однако, расстояние между соседними

значениями аргументов X и Y может достигать 50–250 м, что ведет к

значительным погрешностям отражения поверхностей для пластов с

большими перепадами интерполируемых параметров.

Невозможность точного прохождения поверхности или линии

через заданные (исходные для интерполяции) точки во всех случаях,

кроме совпадения дискретных (сеточных) значений аргументов с ис-

ходными значениями.

При использовании и/или отображении функции требуется рав-

номерная линеаризация каждого участка x

– x

i+1

, y

– y

j+1

(приведение к

плоскости, ограниченной парой треугольников), что не позволяет точ-

но отразить форму поверхности в зонах с резкими перепадами интер-

полируемого параметра (P)

Рассмотрим часто применяемые методы интерполяции.

(4.228)

422

В ходе исследования выявлено, что погрешность построения по-

верхности функции на основе нелинейной интерполяции исходных

данных связана с двумя основными факторами:

−

полученная поверхность проходит вблизи (не пересекает) ис-

ходных точек, а в ряде случаев удалена от них на значительное

расстояние.

−

в сетке поверхности присутствуют необоснованные скачки зна-

чений функции, т.е. интерполируемого параметра – P.

Для оценки качества того или иного метода введем следующие па-

раметры: среднее относительное отклонение (

отн

ср

), коэффициент не-

ровности (k), относительный коэффициент неровности (k

отн

В табл. 4.6 показаны результаты сравнительного анализа методов

интерполяции. Согласно полученным данным и визуальному анализу

напрашиваются следующие виды погрешностей.

Ошибка удаленности точек. Выявлено, что во всех методах, за

исключением методов построения с помощью триангуляции Делоне

полученная поверхность не пересекает исходных точек.

Для того, чтобы определить причины возникновения такой по-

грешности рассмотрим подробнее процесс построения интерполяци-

онной поверхности. Для наглядности изложения будем использовать

систему двух координат, а методом построения – сплайн.

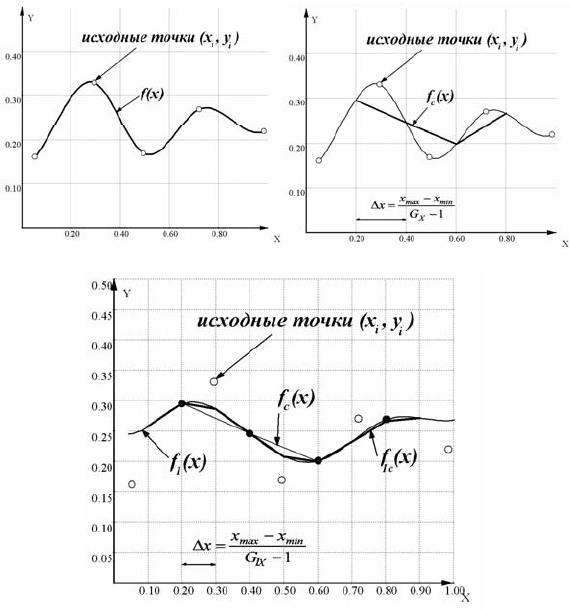
Согласно цели интерполяции, как видно из рис. 4.124 – а, происходит

соединение исходных точек некой плавной линией (например, сплай-

ном). Полученная кривая точно проходит через исходные точки. Для

сеточного представления (хранения) область определения аргумента

на оси Х разбивается на равные интервалы (см. рис.4.124 – б), а точки

пересечения интерполирующей функции f (x) с вертикальными лу

чами

соединяются отрезками прямых линий. Таким образом, получается

результирующая (конечная) сеточная функция – f

(x). Естественно, и

как видно из рис.4.124 – б, она сильно отличается от результата интер-

поляции рис. 4.124 – а и не проходит через исходные точки, так как

выбранное значении G

не удовлетворяет условию точности, однако,

как отмечалось выше, такое условие трудно выполнить из-за большого

объема информации.

423

а) б)

в)

Рис. 4 124. Построение поверхности по сетке координат оси

Х: а – ис-

ходная интерполирующая кривая;

б – переход к сеточному представле-

нию; в – повторная интерполяция с уплотненной сеткой

При построении геологических моделей зачастую используется ме-

тод постепенного уплотнения сетки: в первом приближении выбирает-

ся сетка с малой плотностью G

(с большими приращениями аргумен-

та – Δx), затем, выбирая в качестве исходных точек предыдущую се-

точную функцию – f

(x) (рис. 4.124 – в), увеличивают плотность сетки

до G

и получают следующее приближение – f

(x), которое также пе-

реводят в сеточное представление – f

1с

(x). Данный способ, как видно из

рис. 4.124 – в, ведет к еще большим отклонениям от исходных точек.

424

Единственный способ повышения точности результатов интерпо-

ляции состоит в уплотнении координатной сетки настолько, насколько

это возможно для выполнения условия требуемой точности, или же

следует отказаться от представления искомой интерполирующей

функции в равномерной сетке: необходимо табулировать интерполи-

рующую функцию в неравномерной сетке так, чтобы координаты ис-

ходных точек в плоскости X–Y совп

адали с координатами сетки. Дан-

ный способ связан с негативным фактором увеличения объема данных,

необходимых для хранения поверхности и, соответственно, с невоз-

можностью динамичного ее отображения с помощью имеющихся ком-

пьютерных средств: размер сетки по каждой оси будет равен количе-

ству отличающихся координат исходных точек по этой оси. Например,

если им

еются в качестве исходных данных координаты точек вскры-

тия пластов по 1000 скважинам, то размеры неравномерной сетки бу-

дут в общем случае 1000×1000, что недопустимо для эффективного

использования такой поверхности:

(

)

8239831000100052710

≈

⋅⋅

⋅

Мбайт.

Таким образом, при преоб-

разовании f (x,y) в f

(x,y) про-

исходит неизбежная ошибка.

Описываемая погрешность

может быть также связана не

только с сеточным представ-

лением поверхностей, но и с

особенностями самого метода

интерполяции, т.е. поиска

f (x,y). Зачастую методы ин-

терполяции подменяются ме-

тодами аппроксимации, что

для описания кровли или по-

дошвы пластов неприемлемо.

Рассмотрим ряд примеров

интерполяции то

чек (см. табл.

4.5) поверхности кровли гипо-

тетического пласта с сеткой

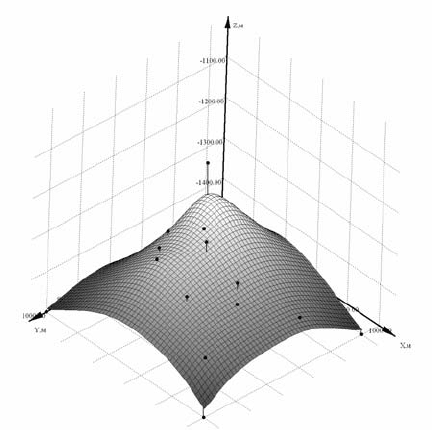
50×50. На рис. 4.125 показан

пример часто возникающей

погрешности интерполяции,

связанной с эффектом чрезмерного сглаживания, т.е. фактически ре-

Таблица 4.5. Исходные точки –

координаты точек пересечения

кровли пласта

Y, м X, м Z=АО, м

0 0 –1500

1000 0 –1500

1000 1000 –1500

0 1000 –1500

500 500 –1300

300 300 –1200

700 500 –1350

100 200 –1600

900 900 –1400

400 700 –1300

350 660 –1350

210 450 –1360

950 350 –1400

770 570 –1370

425

зультаты решения соответствуют аппроксимации, а не интерполяции.

Исходные точки на рис. 4.125 отмечены черными точками, а интерпо-

лирующая сеточная поверхность плоскостями, ограниченными линия-

ми.

Рис. 4.125. Построение поверхности методом Radial Basis

Другим негативным фактором интерполяции являются чрезмерные

отклонения от среднего значения функции.

Чрезмерные биения экстремумов функции связаны с большой

«степенью свободы» интерполяционного метода и соответствующей

ему функции f (x,y) (например, полином n-й степени).

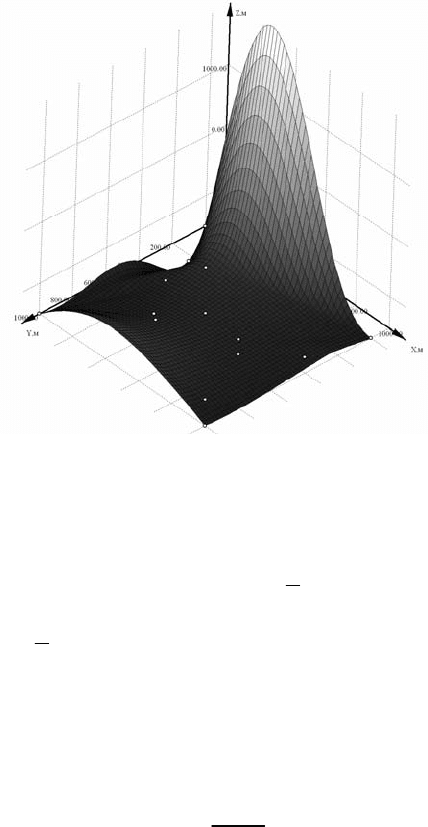
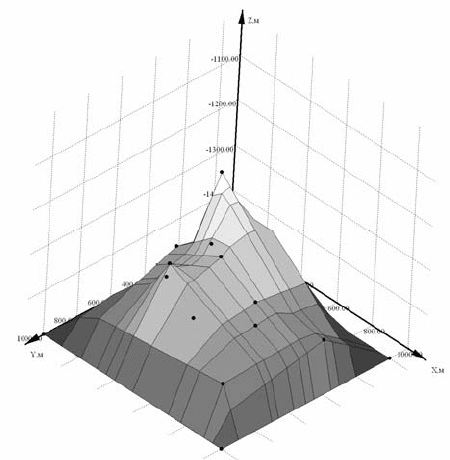
На рис. 4.126 представлена поверхность, простроенная с помощью

метода, разработанного японским ученым Акимой. В сетке поверхно-

сти наблюдаются многочисленные возвышенности и углубления, про-

исхождение которых связано с применением полинома n-й степени в

функции f (x,y) и соот

ветственно с алгоритмом, лежащим в основе ме-

тода. Также негативным фактором является большое отклонение экс-

тремума поверхности: z

max

=2419 м. Положительным свойством данно-

го метода является малое отклонение интерполирующей поверхности

от исходных точек, которое связано только с недостатками сеточного

представления.

426

Рис. 4.126. Интерполирующая поверхность, построенная методом Акима

В ходе анализа выявлено, что аналогичные результаты возникают

во многих методах интерполяции. Проанализируем основные парамет-

ры, позволяющие сравнить качество рассматриваемых методов и ал-

горитмов.

Один из введенных показателей, по которому проводилось сравне-

ние, – среднее относительное отклонение (

ср

) исходных точек от

полученной поверхности по значениям функции.

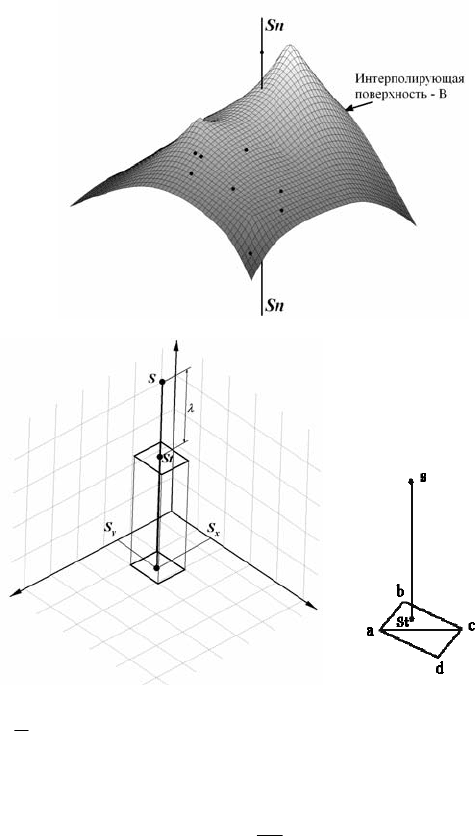
Для расчета

ср

проведем через каждую из n исходных точек луч

Sn (см. рис. 4.127) параллельный оси Z. Затем находим координаты

точки

, лежащей на интерполирующей поверхности («В») в точке

пересечения с лучом Sn. По известным координатам этой и исходной

точки находится длина отрезка ss

, которая является искомым абсо-

лютным отклонением – λ. Затем вычисляется среднее отклонение λ

ср

∑

ср

Недостающей для расчета величиной является значение координа-

ты Z точки

. На первый взгляд можно предположить, что полученная

(4.229)

427

поверхность «В» составлена прямоугольниками, учитывая при этом и

прямоугольную структуру сетки, однако, каждый такой «прямоуголь-

ник» разбит на два треугольника (рис. 4.127 – в). Алгоритм, заложен-

ный в программу (входит в состав [140]) анализа качества интерполя-

ции, проверяет все треугольники на факт пересечения лучом S, оты-

скивая, таким образом, в какой именно треугольник попадает ис

комая

точка (см. рис. 4.127 – в).

Чтобы предотвратить возможные неточности при сравнении по-

верхностей с несовместимыми значениями функции (например, у од-

ной поверхности значения Z исходных точек изменяются в пределах от

0 до 10 м, а у другой – от 0 до 1000 м) необходим относительный па-

раметр – среднее относительное отклонение

ср

minmax

ср

100⋅

−

где z

min

– минимальное значение координаты Z исходных точек;

max

– максимальное значение координаты Z исходных точек.

Данные коэффициенты позволят без визуальной оценки отразить

характер и качество интерполяции тем или иным методом.

Вследствие того, что геометрия пластовой системы достаточно

сложна, оценить качество того или иного метода визуально проблема-

тично. Поэтому зачастую возникают ошибки при выборе метода ин-

терполяции, поверхность которого визуально может бы

ть оценена как

удовлетворительная, а фактически может не выполнять ряд ключевых

условий. Такие условия обычно отражают природную суть геометрии

геологических объектов или физическую суть процессов, протекаю-

щих в ГПП, что особенно касается распределения насыщенностей и

давлений в пластах.

В большей части случаев неточности прогноза показателей разра-

ботки, полученного на основании ис

пользования моделей ГПП, связа-

ны именно с неточным, а зачаcтую с огромными погрешностями, рас-

пределением ФЭС пластов, входящих в систему разработки и эксплуа-

тации месторождения.

Поэтому рассматриваемый анализ качества методов интерполяции,

в конечном счете, необходим для повышения точности моделей ГПП.

(4.230)

428

а)

б) в)

Рис. 4.127. Алгоритм определения среднего относительного отклонения

ср

исходных точек от полученной поверхности по значениям Z

Для оценки степени кривизны (искажения) поверхности, получен-

ной после интерполяции, введем параметр неровности – k:

k =

где F

– площадь получившейся сеточной поверхности;

(4.231)

429

– площадь проекции этой поверхности на плоскость Х–Y

(площадь горизонтальной плоскости, ограниченной минималь-

ными и максимальными значениями координат точек сеточной

поверхности по X и Y).

Коэффициент k может принимать значения больше или равно еди-

нице, так как нелинейная или линейная поверхность будет всегда

иметь площадь больше единицы, за исключением случая, когда он

является плоскостью, параллельной X–Y.

Однако, коэффициент неровности не дает объективных результатов

вследствие того, что неровность поверхности также определяется по-

ложением исходных точек, поэтому для оценки качества метода ин-

терполяции следует ввести относительный коэффициент неровности,

рассчитываемый относительно площади поверхности, полученной ме-

тодом триангуляции Делоне (см. рис. 4.128):

Делоне

отн

Значение данного коэффициента может быть как меньше, так и

больше единицы. Для сглаженных аппроксимирующих поверхностей

данный коэффициент будет меньше единицы, а для хорошо интерпо-

лирующих нелинейных поверхностей будет больше единицы. Чем

меньше

отн

, тем более сглаженный вид имеет поверхность. Мини-

мальное значение коэффициента достигается тогда, когда площадь

поверхности соотвествует площади плоскости, параллельной XY:

Делоне

отн

Для нахождения площади поверхностей находятся и суммируются

площади всех производных треугольников, например для, треугольни-

ка

abc (рис. 4.127– в):

)(P)(P)(PP S cdbcab

abc

−⋅−⋅−⋅=

где Р – полупериметр треугольника abc;

ab, bc, cd – длины сторон треугольника, например

()()()

222

bababaab

ZZYYXX

−+−+−=

где a

, a

и a

– координаты соответствующих точек по осям.

Поскольку исходные точки для сравнения всех методов взяты одни

и те же, в табл. 4.6 от метода к методу мы наблюдаем взаимосвязанное

(4.232)

(4.233)

(4.234)

430

изменение параметров среднего и среднего относительного отклоне-

ния.

Рис. 4.128. Интерполяция методом триангуляция Делоне

Таким образом, можно классифицировать все представленные ме-

тоды построения поверхностей по способу обработки данных на четы-

ре типа:

Вариации метода триангуляции (линейная интерполяция).

Тенденциозное стремление к плоским горизонтальным поверх-

ностям.

Нелинейная интерполяция.

Нелинейная аппроксимация.

К первому типу относятся методы триангуляции Делоне в равно-

мерной и неравномерной сетке (см. рис. 4.128 и рис. 4.130 – а). Ко вто-

рому типу – Nearest Neighbor (см. рис. 4.129). К третьему типу отно-

сятся: ППС-w-cos (см. рис. 4.130 – б), MinimalCurvature и InverseDis-

tance (см. 4.132), П-ППСА (см. 4.133 – б), MidifiedShepard (см. 4.134 –

а), C-ППСА (см. рис. 4.134 – б), метод Акима (см. рис. 4.12

6). К чет-

вертому типу относятся RadialBasis (см. рис. 4.125), Krigging (см. рис.

4.133 – а), П-ППС-w/o-cos и C-ППС-w/o-cos (см. рис. 4.135), П-ППС-