Стрекалов А.В. Математические модели гидравлических систем для управления системами поддержания пластового давления

Подождите немного. Документ загружается.

431

w-cos и C-ППС-w-cos (см. рис. 4.136), Пентоид и Гептоид (см. рис.

4.137).

Методы четвертого типа лучше применять для распределения ФЭС

вследствие того, что исходные точки не являются точными, поэтому

допускается сглаживающая аппроксимация. Методы третьего и перво-

го типа можно применять для формирования геометрии пластов. Тре-

тий тип методов для построения геологических моделей применять

не

желательно.

Методы первого

типа, хотя и не пока-

зывают гладких по-

верхностей, но и не

дают непрогнози-

руемого поведения

интерполирующей

функции в про-

странстве между ис-

ходными точками.

Несмотря не непре-

зентабельный вид

поверхностей, полу-

ченных триангуля-

цией, они являются

наиболее адекват-

ными для формиро-

вания геометрии

пластов, так как в

ни

х отсутствуют пе-

регибы в зонах меж-

ду исходными точками. Разумеется, триангуляционные методы и ме-

тод Nearest Neighbor показывают в приведенном сравнении (см. табл.

4.6) неплохие результаты, но полученная с их помощью форма по-

верхности далека от природной (рис. 4.128, 4.130 – а) вследствие ма-

лого числа образующих плоскостей с выраженными угловыми соеди-

нениями.

Из пр

иведенных методов наиболее эффективными, с точки зрения

точности интерполяции и приемлемости для формирования геометрии

пластов, являются (помере убывания):

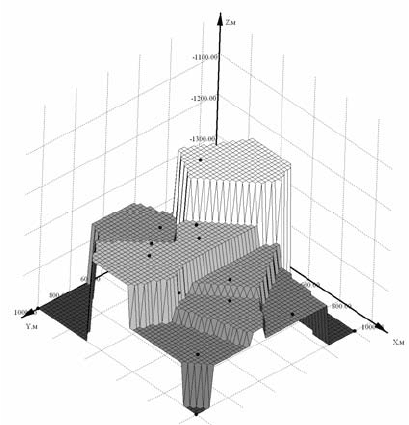
Рис. 4.129. Построение трехмерной поверхности ме-

тодом Nearest Neighbor

432

Основное свойство самого точного метода заключается в том, что

сетка полученной поверхности является неравномерной и подобрана

таким образом, что проходит через исходные точки с образованием в

них сеточных узлов (рис. 4.131 – б). В отличие от первого метода все

остальные имеют равномерные сеточные поверхности и поэтому их

отклонения от исходных точек (за исключением мет

ода Nearest-

Neighbor) отличны от нуля.

Наиболее эффективными для интерполяции/аппроксимации ФЭС

являются:

Как видно из списков, линейная интерполяция с неравномерной

стекой подходит, как для формирования геометрии, так и для распре-

деления ФЭС.

В большинстве проектных и научно-исследовательских институтов

Западной Сибири для построения геологических моделей наиболее

часто используется метод Krigging’а. Однако, как показывает выше-

приведенный анализ, данный метод нельзя применять для построения

геометрии пла

стов и в большинстве случаев для распределения ФЭС,

так как данный метод сильно сглаживает интерполирующую поверх-

ность с подтягиванием «конусов» к исходным точкам (см. рис. 4.133 –

а). Последнее также касается, но в меньшей степени метода Inverse

Distance (см. рис. 4.132 – а).

Линейная интерполяция (неравномерная сетка) (HS)

Nearest Neighbor (Surfer)

Akima (HS)

Modified Shepard (Surfer)

Inverse-Distance (Surfer)

П-ППС-w-cos (HS)

П-ППСА (HS)

Radial Basis (Surfer)

Inverse-Distance (Surfer)

Krigging (Surfer)

Гептоид(HS)

Пентоид (HS)

С-ППС-w/o-cos (HS)

Линейная интерполяция (неравномерная сетка) (HS)

433

а)

б)

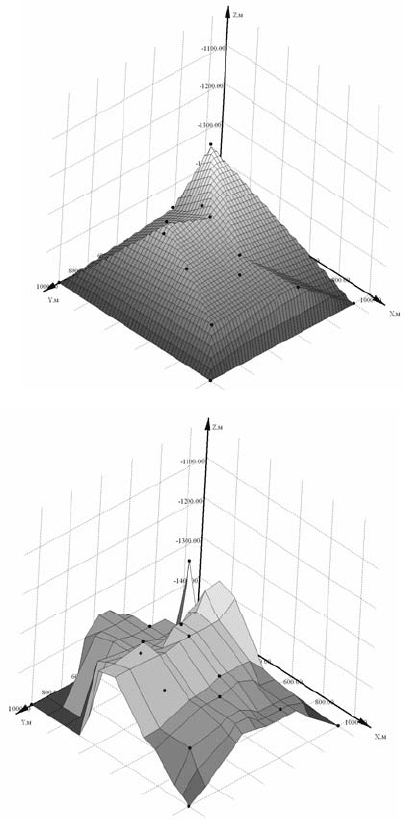
Рис. 4.130. Интерполирующая поверхность:

а – методом триангуляции с

приведением к равномерной сетке;

б – ППС-w-cos (авторский алгоритм,

неравномерная сетка)

434

а)

б)

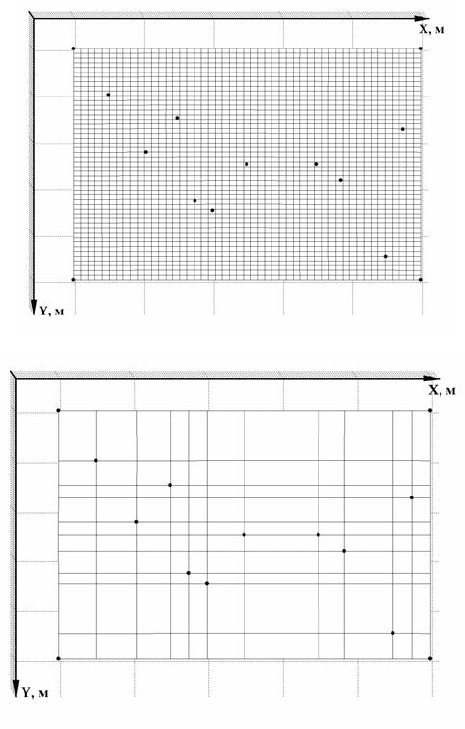
Рис. 4.131. Проекция сетки интерполирующей поверхности на

плоскость

Х–Y: а – всех рассматриваемых методов с равномерной

сеточной поверхностью;

б – всех рассматриваемых методов с не-

равномерной сеточной поверхностью

С точки зрения применимости интерполяционных методов, луч-

шими из них будут те, у которых: 1. среднее относительное отклоне-

435

ние максимально приближено к нулю; 2. коэффициент неровности

максимально мал. Т.е. существует проблема выбора метода под ту или

иную задачу построения геологической модели. Универсальным явля-

ется метод триангуляции Делоне, однако, форма его поверхностей яв-

ляется грубой. Что касается остальных методов, то выбор того или

иного метода зависит от конечного вида поверхности и с

тепени отра-

жения в ней некоторой природной сути или сути физического процес-

са (например, распределения пластового давления).

В заключение анализа выделим основные проблемы использования

методов интерполяции. Неточность построенной на основе нелиней-

ной интерполяции поверхности связана с двумя основными фактора-

ми: полученная поверхность проходит вблизи (не пересекает) исход-

ных точек, а в ряд

е случаев удалена от них на значительное расстоя-

ние; в сетке поверхности присутствуют необоснованные скачки значе-

ний интерполируемого параметра.

Анализ рассмотренных методов установил, что лучшие результаты

показывают наиболее универсальные – триангуляционные методы ли-

нейной интерполяции с неравномерной сеточной поверхностью.

После завершения построения геологической модели на основании

полученной геометрии и распределения ФЭС пл

астов можно описать

исходные данные модели ГПП в виде свойств ячеек (элементов пласта)

– абсолютных проницаемостей, насыщенностей, давлений и открытых

пористостей. Для определения среднего значения параметров в ячейке

значения, полученные из геологической модели, некоторым образом

усредняются между точками на гранях каждой ячейки. Например, для

пластового давления ячейки i:

),Ly,Lx(f

)Ly,Lx(f)Ly,Lx(f

)Ly,Lx(f)y,x(fp

XiXiP

XiXiPXiXiP

XiXiPiiPcli

l,c

l,cl,c

−−+

++−+−++

++++=

∈∈

где c – индекс пласта; l – номер слоя пласта c; P – параметр (пластовое

давление); i – номер ячейки, принадлежащей пласту с и слою l;

l,c

–

интерполирующая функция распределения давления по пласту c, в

слое l, по площади залегания (в плоскости X–Y).

(4.235)

436

Таблица 4.6. Сравнительные показатели методов интерполяции

Для всех

Делоне

=1310984 м

. Примечание: HS – авторский программный

продукт Hydra’Sym; Surfer – часто применяемый программный продукт, предназна-

ченный для построения геологических и картографических моделей.

Название

метода

Среднее

относи-

тельное

отклоне-

ние,

ср

Коэффи-

циент

неровно-

сти к

плоско-

сти, k,

д.е.

Относи-

тельный

коэффи-

циент не-

ровности

отн

, д.е.

Пло-

щадь

полу-

ченной

поверх-

ности,

, м

Radial Basis

(Surfer)

1.469 1.079 0.824 1079880

Inverse-Distance

(Surfer)

0.0737 1.107 0.844 1107064

Krigging (Surfer) 5.357 1.111 0.848 1111388

Гептоид(HS) 0.5380 1.124 0.8574 1124068

Пентоид (HS) 0.4153 1.173 0.8947 1172923

С-ППС-w/o-cos

(HS)

2.957 1.214 0.925 1212528

Линейная интер-

поляция (нерав-

номерная сетка)

(HS)

0 1.247 0.951 1246830

С-ППСА (HS) 1.182 1.293 0.986 1293002

Линейная интер-

поляция (равно-

мерная сетка)

(Surfer)

0.2267 1.297 0.989 1297470

Minimum Curva-

ture (Surfer)

0.1725 1.321 1.01 1328920

С-ППС-w-cos (HS) 1.467 1.332 1.016 1332209

П-ППСА (HS) 0.1157 1.342 0.945 1238516

Modified Shepard

(Surfer)

0.01842 1.539 1.17 1539337

Nearest Neighbor

(Surfer)

0 1.613 1.23 1612756

П-ППС-w-cos (HS) 0.1046 1.659 1.169 1532060

П-ППС-w/o-cos

(HS)

0.3040 1.725 1.215 1592843

Akima (HS) 0.004828 3.346 2.552 3345580

437

а)

б)

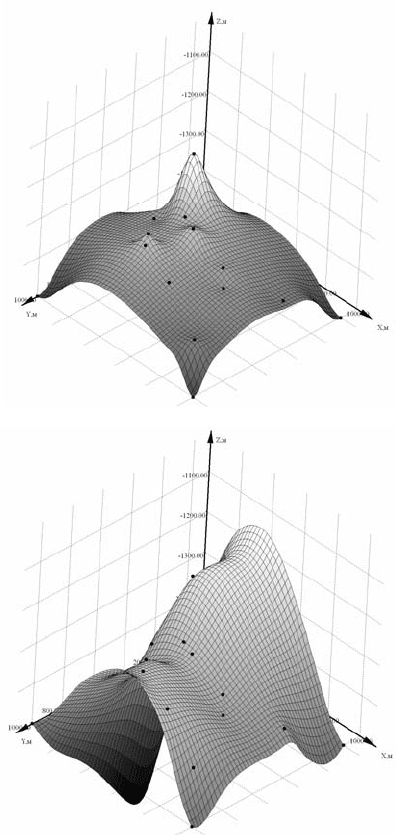
Рис. 4.132. Интерполирующая поверхность:

а – методом

Inverse Distance;

б – методом Minimum Curvature

438

а)

б)

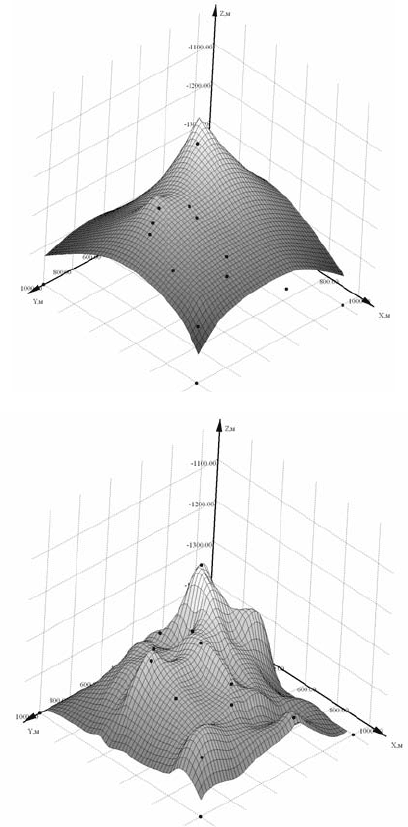
Рис. 4.133. Интерполирующая поверхность:

а – методом Krigging;

б – методом П-ППСА (авторский)

439

а)

б)

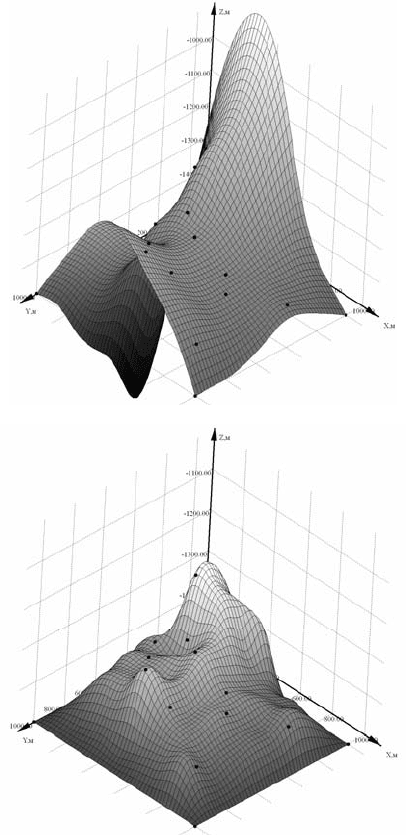
Рис. 4.134. Интерполирующая поверхность:

а – методом Modified

Shepard;

б – методом С–ППСА (авторский)

440

а)

б)

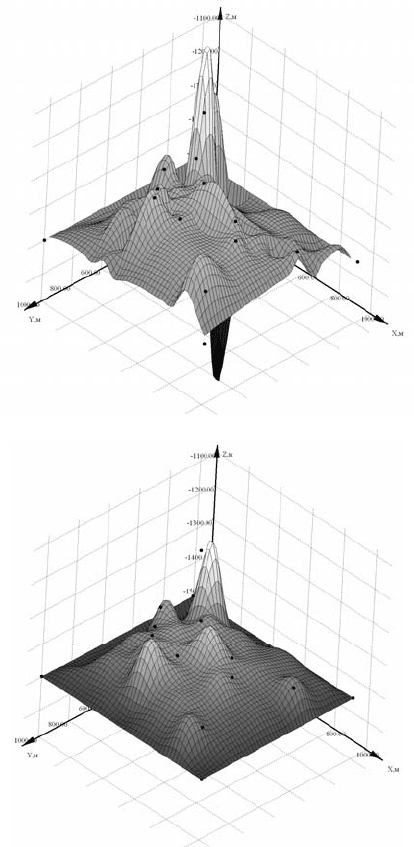
Рис. 4.135. Интерполирующая поверхность:

а – методом П-ППС-w/o-cos

(авторский);

б – методом С-ППС-w/o-cos (авторский)