Стрекалов А.В. Математические модели гидравлических систем для управления системами поддержания пластового давления
Подождите немного. Документ загружается.


391
Основными замыкающими отношениями для ячеек будут зависи-
мости массового расхода компонента Ф, истекающего (или притекаю-
щего) с каждой грани ячейки, от перепада давления для каждого на-
правления фильтрации
)Ф,S(
i
SiU
iSiUi
SiU
iSiUi
Si,Ф
i
SiU,Ф
i
r
zpp
)zpp(sm
Δ+−
=Δ+−=
,
где
)p(Fkk
L
)p(
)p(
R
r
iФSi
)S(
i
Фi
Si
iФ
iФ
)Ф,S(
i
i
)Ф,S(
ρ
μ
ρ
⋅
==
2
1
2
1
–
– приведенное гидравлическое сопротивление течению вдоль оси S,
⎥
⎦
⎤
⎢
⎣
⎡
⋅
кг
сПа
;
(
)
SiU
iiiФ
SiU
i
zz)p(gz −=Δ
ρ
– гидростатический перепад дав-
ления между центром ячейки и гранью U.
При соответствии фильтрации закону Дарси функции
)zpp(s
SiU
iSiUi
Si,Ф
i
Δ+−
можно, в общем, определить согласно из-
вестному сопротивлению, полученному из (4.169)
)Ф,S(
i
Si,Ф
i
r
p
)p(s
Δ
=Δ
,
где
p
Δ
– перепад давления между давлением в центре ячейки и дав-
лением на ее грани SiU.
Так как гидростатический перепад имеет место только по оси Z, да-
лее для удобства изложения мы опустим данный фактор.
Наличие в (4.169) сомножителя –
2
1
подразумевает течение ТС от
центра ячейки – узла p
i
к граням, вследствие чего сопротивление пото-
ку делится пополам, так как расстояние течения от центра до грани
равно половине размера ячейки. Далее относительную проницаемость
ячейки будем обозначать просто
Ф
k
, а абсолютную проницаемость
ячейки
)S(
k
, учитывая, что они относятся к каждой ячейке i. То же
самое, для текущей ячейки i площадь фильтрации обозначим
S
F
, а
длину
S
L
.
Подставив (4.169) в (4.168) и вместо
S
F
соответствующие площа-
ди фильтрации, получим для каждой грани ячейки по осям X, Y и Z
шесть направлений течения компонентов.
(4.168)
(4.169)
(4.169а)
392
Для оси Х:
)p(
L)p(
LLkk)pp(
)pp(sm
iФ
XiФ
ZY
)X(
Ф
Xibi
Xibi
Xi,Ф
i
Xib,Ф
i
ρ
μ
⋅−
=−= 2
.
)p(
L)p(
LLkk)pp(
)pp(sm
iФ
XiФ
ZY
)X(
Ф
Xiei
Xiei
Xi,Ф
i
Xie,Ф
i
ρ
μ
⋅−
=−= 2
.
Для оси Y:
)p(
L)p(
LLkk)pp(
)pp(sm
iФ
YiФ
ZX
)Y(
Ф
Yibi
Yibi
Yi,Ф
i
Yib,Ф
i
ρ
μ
⋅−
=−= 2
.
)p(
L)p(
LLkk)pp(
)pp(sm
iФ
YiФ
ZX
)Y(
Ф
Yiei
Yiei
Yi,Ф
i
Yie,Ф
i
ρ
μ
⋅−
=−= 2
.
Для оси Z:
)p(
L)p(
LLkk)pp(
)pp(sm
iФ
ZiФ
YX
)Z(
Ф
Zibi
Zibi
Zi,Ф
i
Zib,Ф
i
ρ
μ
⋅−
=−= 2
.
)p(
L)p(
LLkk)pp(
)pp(sm
iФ
ZiФ
YX
)Z(
Ф
Ziei
Ziei
Zi,Ф
i
Zie,Ф
i
ρ
μ
⋅−
=−= 2
.
Вследствие того, что фильтрационные свойства коллекторов суще-
ственным образом изменяются в зависимости от давления [164], необ-
ходимо иметь в виду и этот фактор. Если учесть изменение абсолют-
ной проницаемости от давления согласно (4.148), то замыкающие от-
ношения изменятся следующим образом
)p(
L)p(
Fekk)pp(
)pp(sm
iФ
SiФ
S
)Pp(n
)S(
Ф
Sibi
SiUi
Si,Ф
i
SiU,Ф
i
ii
ρ
μ
0
0
2
−
⋅−
=
=−=
,
где n – коэффициент изменения проницаемости от давления;
)(
0
S
k
– начальная абсолютная проницаемость при начальном
пластовом давлении –
0
i
P
вдоль оси S.
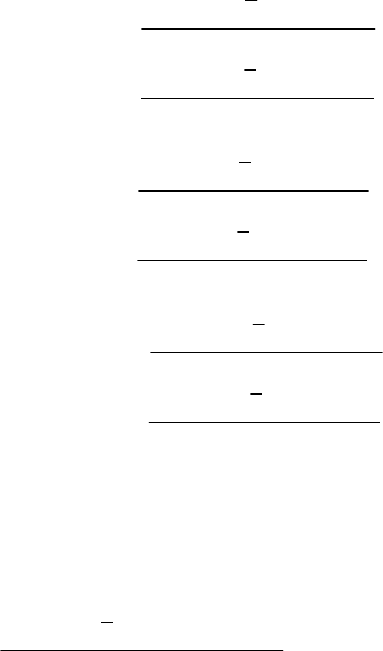
Описанные отношения соответствуют линейному закону фильтра-
ции каждого компонента. Если предполагается учесть нарушение ли-
нейного закона, которое наблюдается при высоких скоростях фильтра-
(4.170)
393
ции [244], то (4.168 и 4.170) будут использоваться для нахождения
)p(s
Si,Ф
i
Δ
при Δp <
кр
p
Δ
, где
кр
p
Δ
– перепад давления, соответствую-
щий точке перехода в нелинейный закон фильтрации, который может
быть определен согласно критическому числу Re
кр
[
]
121..
∈
(см. фор-
мулу 4.135).
Для описания фильтрации, не соответствующей линейному соот-
ношению перепада давления и массового расхода, будем использовать
функцию
)p(
Si,Ф
i
Δ
σ
, которая необходима для определения массового
расхода компонента Ф при Δp >
кр
p
Δ
. Таким образом, закон фильтра-
ции в ячейке в зависимости от направления потоков будет составным,
а функцией, отражающей такой закон, будем называть
)p(
Si,Ф
i
Δ
ζ
=
)p(s
Si,Ф
i
Δ
при Δp<
кр
p
Δ
,
)p(
Si,Ф
i
Δ
ζ
=
)p(
Si,Ф
i
Δ
σ
при Δp>
кр
p
Δ
.
Требованием к зависимости
)p(
Si,Ф
i
Δ
σ
будет выполнение сле-
дующих условий.
1.
Равенство первых производных на границе перехода линейного
закона в нелинейный (точка
кр
p
Δ
):
)p(s)p(
кр
Si,Ф
iкр
Si,Ф
i
Δ
′
=Δ
′
σ
.
2.
Равенство функций в точке
кр
p
Δ
:
)p(s)p(
кр
Si,Ф
iкр
Si,Ф
i
Δ=Δ
σ
.
На рис. 4.115 показан пример составной функции
)p(
Si,Ф
i
Δ
ζ
. В ка-
честве примера для описания нелинейного закона фильтрации возьмем
следующую зависимость
=
Δ
)
p
(
σ
ApB +Δ
ϕ
,
где
ϕ
, В и А – фильтрационные коэффициенты, причем,
ϕ
– свобод-
ный коэффициент, а А и В определяются исходя из условий (4.172–
4.173).
Для выполнения условий (4.172) и (4.173) необходимо решить сис-
тему из двух уравнений. С целью упрощения изложения введем сле-
дующие обозначения. Для линейных отношений закона фильтрации
запишем (4.168) в виде
(4.171)
(4.172)
(4.173)
(4.174)
394
p)p
(
s
Δ
=
Δ
α
,
где
)Ф,S(
i
r
1
=
α
– фильтрационный коэффициент для линейного закона.
Рис. 4.115. Функция составного закона фильтрации
Система уравнений в общем виде выглядит так:
(
)
(
)
()()
⎪
⎩
⎪
⎨
⎧
Δ
′
=Δ
′
Δ=Δ
кркр
кркр
pps
pps
σ
σ
,
а относительно неизвестных коэффициентов А и В для рассматривае-
мого примера нелинейного закона фильтрации согласно (4.174)
⎪
⎩
⎪
⎨
⎧
Δ=
+Δ=Δ
− )(
кр
кркр
pB
ApBp
1
ϕ
ϕ
ϕα
α
.
Отсюда
)(
кр
p
B
1−
Δ
=
ϕ
ϕ
α
и
ϕ
ϕ
ϕ
α
α
кр
)(
кр
кр
p
p
pA Δ
Δ
−Δ=
−1
.
Подставив данные коэффициенты в (4.174), получим нелинейный
закон фильтрации
(4.177)
(4.178)
(4.175)
(4.176)
395
ϕ
ϕ
ϕ
ϕ
ϕ
α
α
ϕ
α
σ
кр
)(
кр
кр
)(
кр
p
p
pp
p
)p( Δ
Δ
−Δ+Δ
Δ
=Δ
−− 11
,
причем, прямая линейного закона
)
p
(
s
Δ
будет плавно переходить в
кривую
)
p
(
Δ
σ
, описанную (4.179), так как фильтрационные коэффи-
циенты связаны коэффициентом
α
линейного закона
)
p
(
s
Δ
. Свобод-
ный коэффициент –
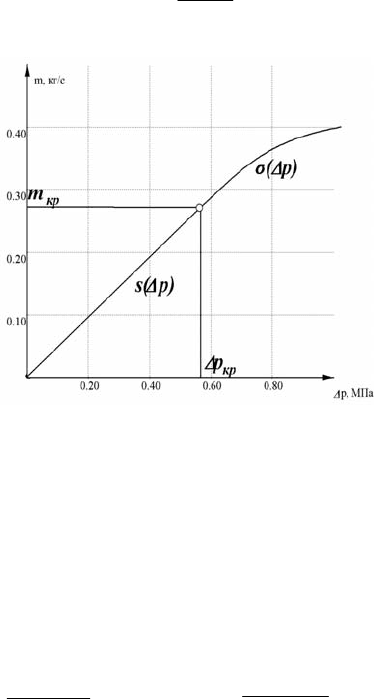
ϕ
отражает характер нели-
нейного закона (см. рис.
4.116).
Для определения точ-
ки –
кр
pΔ
перехода ли-
нейного закона в нели-
нейный, будем исходить
из критического массо-
вого расхода –
SiU,Ф
i
M
′
в
ячейке i вдоль оси S от
центра к грани U, опре-
деляемого линейным
соотношением
)p(
L)p(
Fkkp
)p(sM
iФ
SiФ
S
)S(
Ф
кр
кр
Si,Ф
i
SiU,Ф
i
ρ
μ
⋅⋅Δ
=Δ=
′
2
.
Для нахождения критического массового расхода в ячейке i вдоль
оси S из формулы (4.135) после подстановки зависимостей плотности
)p(
iФ
ρ
и динамической вязкости
)p(
iФ
μ
от давления, фазовой
проницаемости
)S(
Ф
kkk ⋅=
по оси S и скорости в виде отношения
массового расхода к площади фильтрации и плотности имеем крите-
рий фильтрации
()
)p(
)p(
m
kk
F)p(
M
Re
iФ
iФ
.
отк
)S(
Ф
SiФ
SiU,Ф
i
кр
ρ
μ
ρ
32
10
′
=
,
соответствующий точке массового расхода
SiU,Ф
i
M
′
– нарушения ли-
нейного закона фильтрации, выше которого нарушается линейное со-
отношение перепада давления и расхода ТС. Здесь m
отк
– открытая
пористость.
(4.181)
(4.179)
(4.180)
Рис. 4.116. Составной закон фильтрации для
различных коэффициентов
ϕ
при
α
= 1

396
Отсюда критический массовый расход в ячейке будет определять-
ся следующей формулой:
(
)
)S(
Ф
iФ
.
эф
Sкр
Si,Ф
i
kk
)p(mFRe
M
10
32
μ
=
′
.
Совместив (4.182) и (4.180) приравниванием правых частей, полу-
чим уравнение
()
)p(
L)p(
Fkkp
kk
)p(mFRe
iФ
SiФ
S
)S(
Ф
кр
)S(
Ф
iФ
.
эф
Sкр
ρ
μ
μ
⋅⋅Δ
= 2
10
32
,
откуда выразим
кр
pΔ
, соответствующий точке (см. рис. 4.115) наруше-
ния закона Дарси
(
)
()
)(20
)(
Re
5.1
)(
2
3.2
iФ
S
Ф
SiФ
эф
кркр
pkk
Lpm
p
ρ
μ
⋅
=Δ
.
Таким образом, при расчете функций составного закона фильтра-
ции
)pp(
SiUi
Si,Ф
i
−
ζ
, если
SiUi
pp −
>
кр
p
Δ
, то расчет массового рас-
хода следует проводить по функции
)p(
Si,Ф
i
Δ
σ
, а если
SiUi
pp −
≤
кр
pΔ
, то по функции
)p(s
Si,Ф
i
Δ
.
Далее под замыкающими отношениями, описывающими энергети-
ческое воздействие ячейки в различных направлениях фильтруемых
компонентов, будем понимать функции
)p(
Si,Ф
i
Δ
ζ
. Особенно важно
отметить, что
)p(
Si,Ф
i
Δ
ζ
должна быть нечетной функцией, т.е.
)p()p(
Si,Ф
i
Si,Ф
i
Δ−−=Δ
ζζ
. Поэтому при нахождении зависимости
(4.179) необходимо понимать под
кр
p
Δ
модуль перепада давления, а
вид
)
p
(
Δ
σ
должен численно приводиться к нечетному виду:
ϕ
ϕ
ϕ
ϕ
ϕ
α
α
ϕ
α
σ
кр
)(
кр
кр
)(
кр
p
p
pp
p
)p( Δ
Δ
−Δ+Δ
Δ
=Δ
−− 11
при
0>
Δ
p
,
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
Δ
−Δ+Δ
Δ
−=Δ
−−
ϕ
ϕ
ϕ
ϕ
ϕ
α
α
ϕ
α
σ
кр
)(
кр
кр
)(
кр
p
p
pp
p
)p(
11
при
0
<
Δ
p
Для учета двухкомпонентной фильтрации необходимо описать за-
висимость относительной проницаемости каждого компонента от на-
(4.182)
(4.183)
(4.184)
397
сыщенностей ими порового пространства, данные зависимости обычно
устанавливаются эмпирически [165, 199, 209] и реже теоретически
[197]. Степень влияния изменения фазовых проницаемостей в зависи-
мости от насыщенности фаз на результаты расчета перетока между
элементами ГПП огромна [203], и неточность описания данных зави-
симостей чревата большими погрешностями моделирования. Особенно
сильно неточность расчета относительных или фазовых проницаемо-
стей ск
азывается при учете совместной фильтрации в трещинах и по-
ровом пространстве [214].
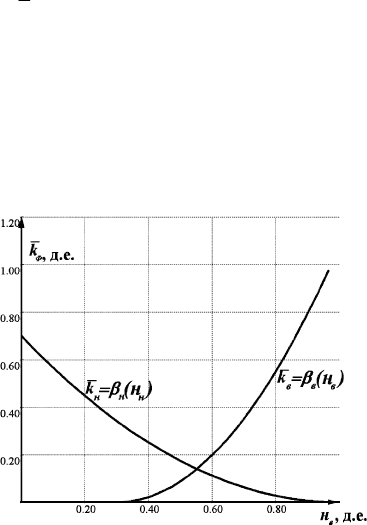
Если обозначить коэффициент насыщенности компонента Ф в
ячейке i как
Фi
н , то относительные проницаемости будут представ-
лены функциями
)н(k
ФiФ
Фi
β
=
для каждого компонента, где в качестве аргумента выступает текущая
насыщенность компонента в ячейке. На рис. 4.117 показан пример та-
ких функций для воды и нефти. Из графиков на рис. 4.117 видно, что с
ростом насыщенности одного компонента падает относительная про-
ницаемость другого. Причем, при насыщенности одного из компонен-
тов ниже определенной величины относительная п
роницаемость этого
компонента равна нулю, т.е. фильтрации не происходит. Это объясня-
ется капиллярными яв-
лениями в поровых ка-
налах: при достижении
некоторой минималь-
ной насыщенности
компонента в поровом
пространстве его филь-
трация невозможна
вследствие того, что
молекулы компонента
связаны взаимодейст-
вием с молекулами
породы. Доли нефти
или воды, неизвлекае-
мые из п
орового про-
странства, иногда на-
зывают «погребенны-
ми».
(4.185)
Рис. 4.117. Пример зависимостей относительных
проницаемостей воды и нефти от насыщенности
воды
398
Рассмотренные выше задачи относятся к моделированию фильтра-
ционных процессов, которые отражаются в виде замыкающих отноше-
ний
)p(
Si,Ф
i
Δ
ζ
при установившейся фильтрации в течение некоторого
времени Δt. Здесь следует также учитывать некоторый перепад давле-
ния, ниже которого фильтрации компонента Ф не происходит, т.е.
0)(
,
=Δp
SiФ
i
ζ
при
Ф
Sк
pp Δ<Δ , где
Ф
Sк
pΔ – перепад давления между
центром и гранью ячейки по оси S, при котором и выше которого воз-
можна фильтрация компонента Ф. Необходимость учета данного фак-
тора продиктована капилярными силами и возможными реолигиче-
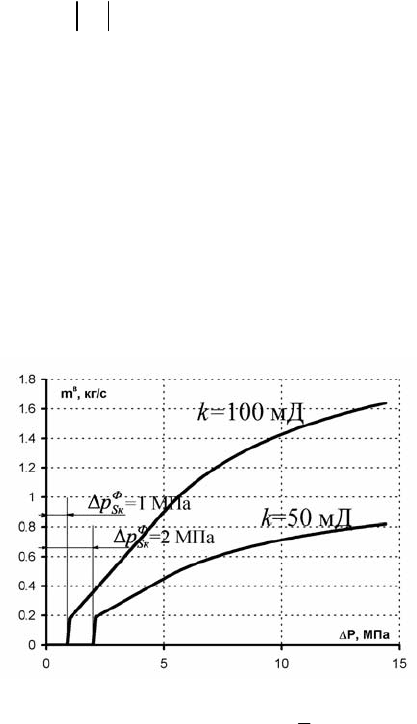
скими свойствами компонентов [166, 200]. На рис. 4.117/1 показаны
примеры зависимостей
)(
,
p
SФ
i
Δ
ζ
для различных проницаемостей и
величин
Ф
Sк
pΔ . Величина
Ф
Sк
pΔ для показанных примеров взята про-
извольно, для реальных условий перепад давления на участке длиной
L
S
=5 м колеблется в пределах от 0 до 0.05 МПа. Велична
Ф
Sк
pΔ опре-
деляется согласно градиенту давления –
Ф
Sк
dp , при котором возможна
фильтрация компонента (для полной длины ячейки вдоль оси S):
S
Ф
Sк
Ф
Sк
Ldpp ⋅=Δ
, где
[]
01.0..0∈
Ф
Sк
dp
МПа/м.
Рис. 4.117/1. Примеры расчетных зависимостей
)(
,
p
SФ
i
Δ
ζ
при
)(S
k =100
и 50 мД,
кр
pΔ = 5 МПа, L
S
=5 м, F
S
=25 м
2
,
в
k =0.4,
μ
в
=1.8 мПа⋅с
399
Следующим процессом, рассматриваемым при моделировании эле-
ментов пласта, является процесс деформации породы[195] и порового
пространства в зависимости от притока и оттока компонентов из ячей-
ки, т.е. изменение емкостных свойств ячейки в зависимости от притока
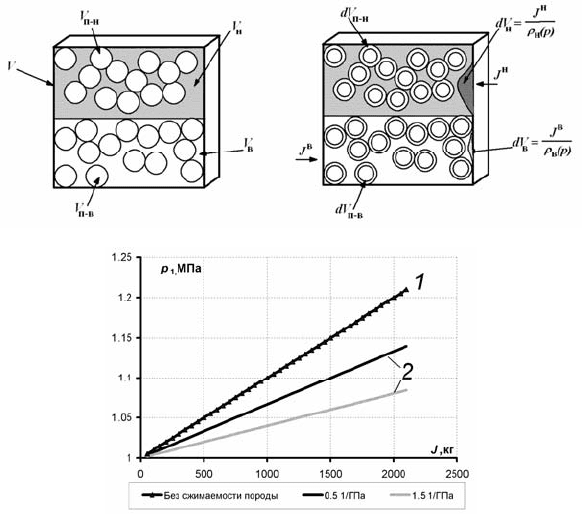
или оттока масс компонентов (рис. 4.118).
а)
б)
Рис. 4.118. Схема притока объемов двух компонентов при деформации:
а –
схема деформации породы в ячейке;
б – зависимость давления от притока
массы ТС,
1 – без учета дефорации породы, 2 – с учетом деформации по-
роды
Допустим, на данный момент времени известны массовые расходы
потоков, истекающих из ячейки i со всех ее граней. Причем, так как
рассматриваются перепады давления между центром и гранями ячей-
ки, если
SiU,Ф
i
m
> 0, то происходит истечение компонента Ф из ячейки
по направлению оси S с грани U, а если
SiU,Ф
i
m
< 0, то приток в ячейку
извне через эту грань в этом направлении. Таким образом, суммарное
400
приращение массы компонента Ф в ячейке i будет равно сумме произ-
ведений всех массовых расходов
SiU,Ф
i
m
за время Δt по всем шести
граням (так как приток
SiU,Ф
i
m
<0, то приращение массы со знаком
«–»):
∑
=
=
⋅Δ−=
6
e,bU
Z,Y,XS
SiU,Ф
i
Ф
i
mtJ
.
Вследствие деформации породы и компонентов при
Ф
i
J
> 0 порода
и компоненты будут сжиматься, а при
Ф
i
J
< 0 разжиматься, при этом
будут изменяться их плотность и занимаемый объем в соответствии с
коэффициентами сжимаемости (см. рис. 4.118).
В зависимости от учета факторов изменения или постоянства объе-
ма ячейки V и объема, занимаемого компонентами, модель деформа-
ционных процессов в ячейке может быть четырех видов.
1. Исходя из постоянства объема ячейки и постоянства об
ъема по-
рового пространства, рассчитывается изменение давления в ячейке
вследствие приращения массы некоторой одной сжимаемой жидкости.
2. Исходя из постоянства объема ячейки и изменения объема поро-
вого пространства, рассчитывается изменение давления в ячейке
вследствие приращения массы некоторой одной сжимаемой жидкости.
3. Исходя из постоянства объема ячейки и изменения объема поро-
вого пространства, рассчит
ывается изменение давления в ячейке
вследствие приращения масс нескольких сжимаемых текучих сред.
4. Подразумевая непостоянство объема ячейки и объема порового
пространства, рассчитывается изменение давления в ячейке вследствие
приращения масс нескольких сжимаемых текучих сред.
Для дальнейшего изложения зададимся коэффициентами сжимае-
мости для каждого компонента –
Ф
w
, породы –
п
w
и объемами, зани-
маемыми породой – V
п
и каждым компонентом – V
Ф
.
Для упруго-сжимаемых сред известно соотношение
V
wdpdV ⋅
⋅
−
=
,
где w – сжимаемость вещества, Па
-1
;
dp – изменение давления;
dV – изменение объема;
V – объем, занимаемый до изменения давления.
(4.186)
(4.187)
