Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

1.4 Exercises

CONCEPTS

Fundamentals

1. (a) A relation is a function if each input corresponds to exactly one _______.

(b) If two-variable data are given in a table and the variable y is a function of the

variable x, then

_______ is the independent variable and _______ is the

dependent variable.

2. (a) To find out whether an equation in x and y determines y as a function of x, we first

solve the equation for

_______. If an equation defines y as a function of x, then

how many y values correspond to each x value?

(b) The equation defines y as a function of x, so

_______ is the

independent variable and

_______ is the dependent variable.

3. The equation defines y as a function of x. Then the net change of the

variable y from to is

_______  _______  _______.

4. (a) To determine whether a graph defines y as a function of x, we use the

_______

_______ Test.

(b) Which of the following are graphs of functions of x?

x = 4x = 0

y = x

+ 2

y = x

+ x + 1

44 CHAPTER 1

■

Data, Functions, and Models

Test your skill in solving equations. You can review this topic in

Algebra Toolkit

C.1

on page T47.

1–4 Solve the equation for x.

1. 2.

3. 4.

5–8 An equation in the variables x and y is given.

(a) Find the value(s) of y when x is 3.

(b) Find the value(s) of x when y is 2.

5. 6.

7. 8.

9–18 An equation in two variables is given. Solve the equation for the

indicated variable.

9. ; x 10. ; T

11. ; 12. ; y

13. ; t 14.

15. ; t 16. ; h

17. ; y 18. ; R

p - R

=-8py

- 9x = 0

wh = 3h + 2st + 4t = 3s

;p

= 3x

8x - y

= 0zr - 2z = z

P = 6Ty = 5 + 3x

3x - y

= 0y

= x

+ 18

x = y

- 1y = 5 + 3x

8 = 31x + 22- 1271x - 22= 5x + 6

7 + 17x = 3x3x - 5 = 4

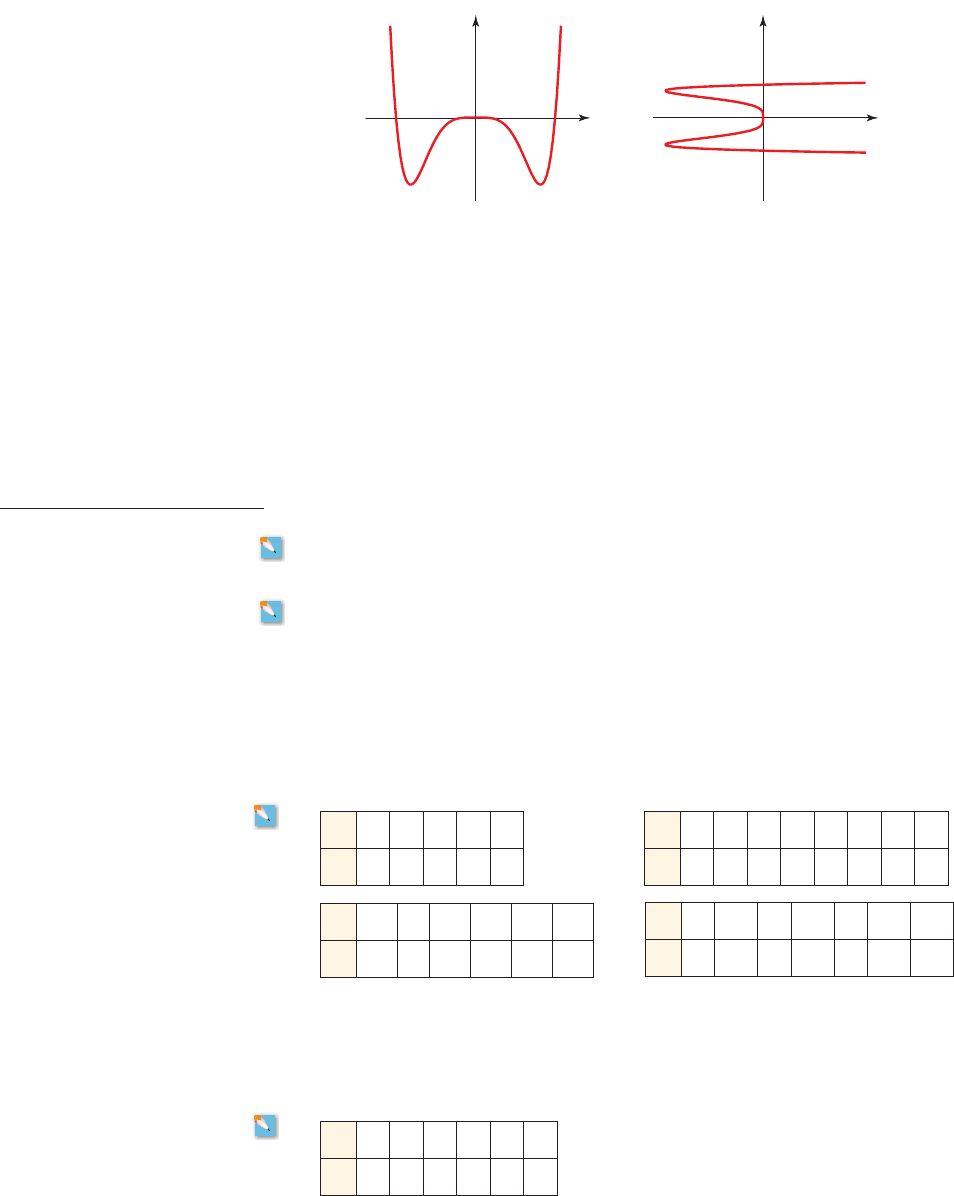
SECTION 1.4

■

Functions: Describing Change 45

SKILLS

(i)

(ii)

x 0 1 1 9 9 81 81

y 0

- 1

- 3

- 9

Think About It

5. True or false?

(a) All relations are functions.

(b) All functions are relations.

(d) Some functions can be defined by an equation.

6. In this section we represented functions in four different ways. Think of a function that

can be represented in these four ways, and write down the four representations.

7–10

■ A set of ordered pairs defining a relation are given. Is the relation a function?

10.

11–14

■ Two-variable data are given in a table.

(a) Is the variable y a function of the variable x? If so, which is the independent

variable and which is the dependent variable?

(b) Is the variable x a function of the variable y? If so, which is the independent

variable and which is the dependent variable?

11. 12.

13. 14.

15–18

■ Two-variable data are given in the table.

(a) Explain why the variable y is a function of the variable x.

(b) Find the net change in the variable y as x changes from 0 to 5.

15.

x 0 1 2 3 4 5

y 2 0 3 4 2 1

x 1 2 3 4 5 6

y 10 9 10 15 10 21

x 0 1 2 3 4 5 6 7

y 6 6 6 6 6 6 6 6

x 1 2 2 4 4

y 6 9 3 2 8

51- 2, - 1 2, 1- 1 , - 12, 10, - 12, 11, - 12, 12, - 12, 13, - 126

513, 42, 14, - 12, 13, 5 2, 1- 1, 52, 13, 92, 1- 2, 726

511, 42, 12, 62, 13, 12, 13, 726

511, 22, 1- 1, 22, 13, 5 2, 1- 3, 52, 15, 82,

1- 5, 826

16.

17.

18.

19–22

■ An equation is given in function form.

(a) What is the independent variable and what is the dependent variable?

(b) What is the value of the dependent variable when the value of the independent

variable is 2?

19. 20.

21. 22.

23–28

■ An equation is given.

(a) Does the equation define y as a function of x?

(b) Does the equation define x as a function of y?

23. 24.

25. 26.

27. 28.

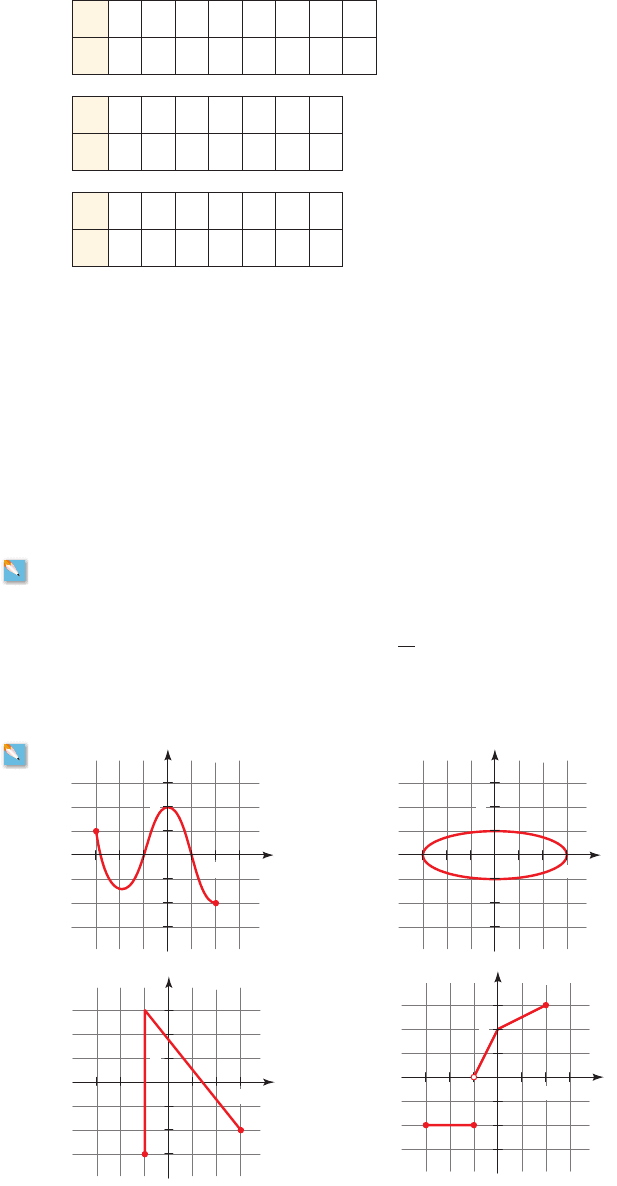
29–32

■ Use the Vertical Line Test to determine whether the graph determines y as a

function of x. If so, find the net change in y from to .

29. 30.

x = 2x =-1

+ 3y = 01y + 32

+ 1 = 2x

1y + 32

+ 1 = x

+ 2 = y

2y + 3x

= 02y + 3x = 0

z = 51y + 22

w = 5l

+ 3l

x = 2y + 1y = 3x

+ 2

x 0 1 2 3 4 5 6

y 2 4 7 10 6 3 1

x 0 1 2 3 4 5 6

y 3 4 5 6 5 4 3

x 0 1 2 3 4 5 6 7

y 6 6 6 6 5 5 5 5

31. 32.

33–36 ■ An equation and its graph are given. Use the Vertical Line Test to determine

whether the equation defines y as a function of x.

46 CHAPTER 1

■

Data, Functions, and Models

SECTION 1.4

■

Functions: Describing Change 47

35. 36. x

+ y

- x

= 644y

- 3x

= 1

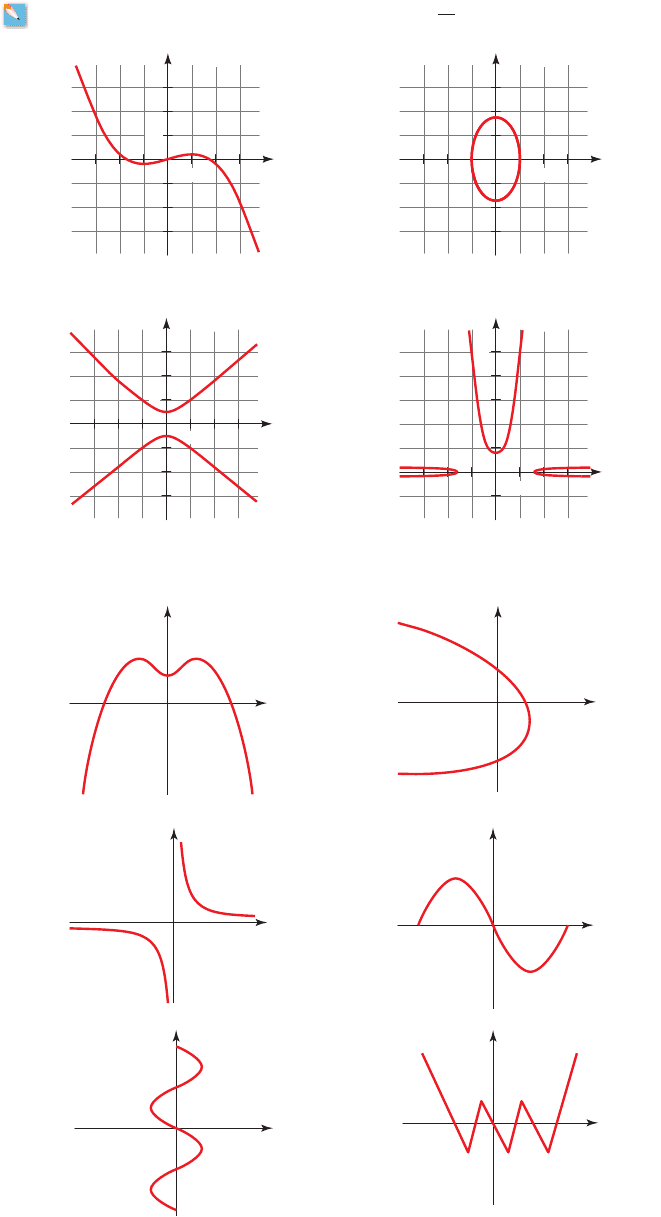
37–42

■ Use the Vertical Line Test to determine whether the graph determines y as a

function of x.

37. 38.

39. 40.

41. 42.

33. 34. x

= 1y = 3x - x

48 CHAPTER 1

■

Data, Functions, and Models

43–48

■ An equation is given.

(a) Make a table of values and sketch a graph of the equation.

(b) Use the Vertical Line Test to see whether the equation defines y as a function of x.

If so, put the equation in function form.

43. 44.

45. 46.

47. 48.

49–52

■ A verbal description of a function is given. Find (a) algebraic, (b) numerical, and

49. “Multiply the input by 3 and add 2 to the result.”

50. “Subtract 4 from the input and multiply the result by 3.”

51. The amount of sales tax charged in Lemon County on a purchase of x dollars. To find

the tax (the output), take 8% of the purchase price (the input).

52. The volume of a sphere of diameter d. To find the volume (the output), take the cube of

the diameter (the input), then multiply by and divide by 6.

53. Big Box Retail Stores The number of “big box” retail stores has increased

nationwide in recent years. The following table shows the number of existing big box

retail stores and the median home price for a certain region for the years 1997–2006.

(a) Show that the variable is not a function of the variable y.

(b) Show that the variable y is a function of the variable x. Find the net change in the

number of big box stores from 2003 to 2005 and from 1997 to 2006.

median home price from 1997 to 2006.

5y = x

- x = 0

1y + 32

= x1y - 22

= 2x

x = 2y

y = 2x

CONTEXTS

Year

Number of big

box retail stores

Median home

price (dollars)

1997 27 145,000

1998 30 150,000

1999 32 162,000

2000 38 187,000

2001 38 190,000

2002 42 199,000

2003 46 195,000

2004 46 200,000

2005 46 210,000

2006 49 230,000

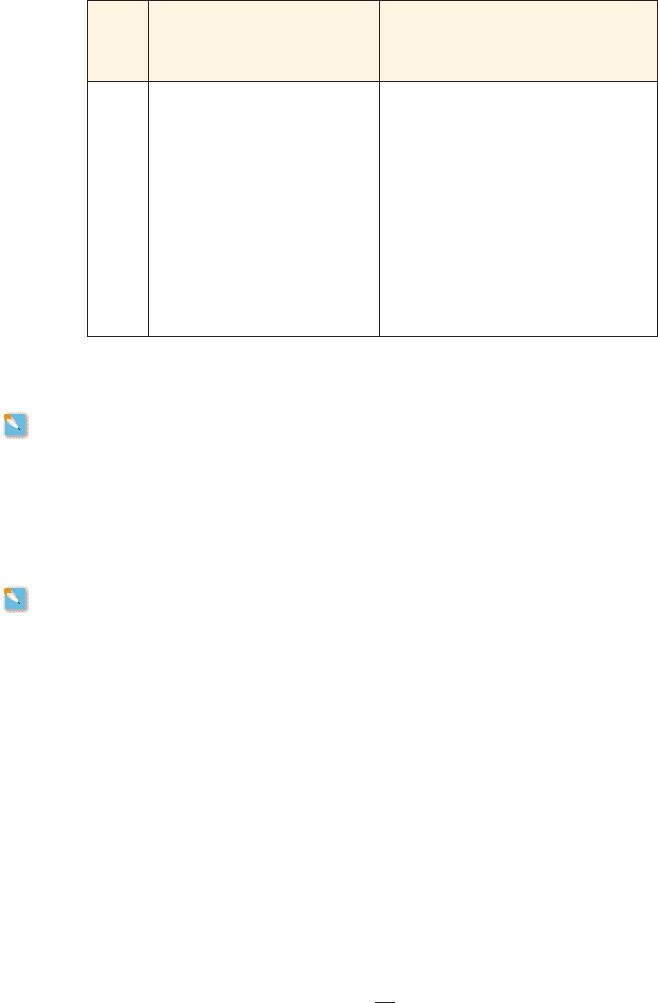
54. World Consumption of Energy The table on the following page shows the yearly

world consumption of petroleum and coal from 1995 to 2005.

(a) Show that the variable is not a function of the variable y.

(b) Show that the variable y is a function of the variable x.

1995 to 2005.

(d) Show that the variable is a function of the variable x.

(e) Find the net change in the world consumption of petroleum from 1995 to 2005.

SECTION 1.4

■

Functions: Describing Change 49

Year

World consumption of coal

(millions of tons)

World consumption of petroleum

(quadrillions of BTUs)

1995 88 142

1996 90 146

1997 92 149

1998 90 150

1999 92 153

2000 94 155

2001 95 157

2002 98 158

2003 107 161

2004 116 167

2005 123 169

55. Deliveries A feed store charges $25 for a bale of hay plus a $15 delivery charge. The

cost of a load of hay is a function of the number x of bales purchased. Express this

function verbally, symbolically, numerically, and graphically.

56. Cost of Gas Simone rents a compact car that gets 35 miles per gallon. When she rents

the car, the price of a gallon of gas is $3.50. The cost C of the gas used to drive the car

is a function of the number of miles x that the car is driven. Express this function

verbally, symbolically, numerically, and graphically.

57. Profit A university music department plans to stage the opera Carmen. The fixed cost

for the set, costumes, and lighting is $5000, and they plan to charge $15 a ticket. So if

they sell x tickets, then the profit P they will make from the performance is given by the

equation

(a) Show that P is a function of x.

(b) Find the net change in the profit P when the number of tickets sold increases from

100 to 200.

(d) Find the net change in the number of tickets sold when the profit changes from $0

to $5000.

58. Flower Bed Mulch Susan manages a landscape design business that operates in a

suburb of Philadelphia. In the fall, her customers need mulch for all of their flower

beds. If Susan has x square feet of flower beds to mulch, then the number y of cubic

yards of mulch she needs is given by the equation

(a) Show that y is a function of x.

(b) Find the net change in the amount of mulch y when the area of the flower beds

increases from 10 to 50 square feet.

(d) Find the net change in the area x of flower beds mulched when the amount of

mulch increases from 2 to 20 cubic yards.

y =

P = 15x - 5000

50 CHAPTER 1

■

Data, Functions, and Models

60. Relativity According to the Theory of Relativity, the length of an object depends on

its velocity √ with respect to an observer. For an object whose length at rest is 10 m, its

observed length L satisfies the equation

where c is 300,000 km/s, the speed of light.

(a) Express L as a function of √.

(b) What is the observed length L of a meteor that is 10 m long at rest and that is

traveling past the earth at 10,000 km/s?

traveling at 5000 km/s?

(d) What is the net change in the observed length L of an object whose velocity

changes from 5000 km/s to 10,000 km/s?

61. Women and Cancer Linda knows quite a few women who have been diagnosed with

breast cancer. She decides to make a table of these women’s current ages and the age at

which they were diagnosed with breast cancer.

(a) Graph the relation between current age and age at diagnosis.

(b) Use the Vertical Line Test to determine whether the variable y is a function of the

variable x.

+ 100√

= 100c

62. Data A college algebra class collected some data from their classmates. The table at

the top of page 51 lists some of these data.

(a) Graph the relation (x, y), where x is height and y is weight. Use the Vertical Line

Test to determine whether the variable y is a function of the variable x.

(b) Graph the relation (x, y), where x is age and y is year of graduation. Use the Vertical

Line Test to determine whether the variable y is a function of the variable x.

0.5 cm

5'0"

5'6"

6'0"

6'6"

Current age

Age at diagnosis

63 50

72 65

45 35

62 60

62 54

71 66

59 54

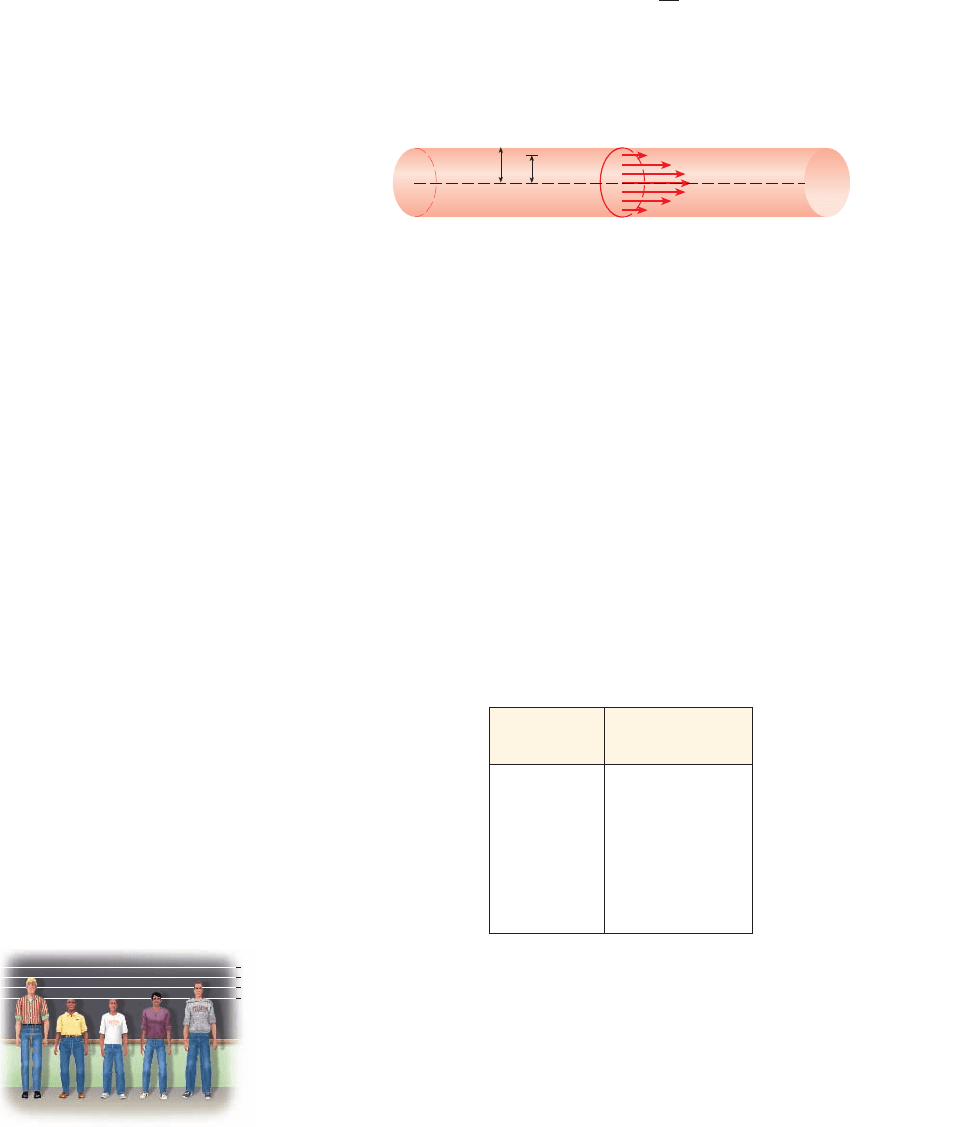
59. Blood Flow As blood moves through a vein or an artery, its velocity √ is greatest along

the central axis and decreases as the distance r from the central axis increases (see the

figure). The equation that relates √ and r is called the Law of Laminar Flow. For an artery

with radius 0.5 cm, the relationship between √ (in cm/s) and r is given by the equation

(a) Express √ as a function of r.

(b) What is the velocity √ when the distance r from the central axis is 0, 0.1, and 0.5 cm?

and when the distance r changes from 0.1 to 0.5 cm?

= 0.25 -

√

SECTION 1.4

■

Functions: Describing Change 51

ID Age Height Weight

Graduation

year

54-6514 21 72 in. 170 lb 2008

25-9778 18 67 in. 204 lb 2010

60-5213 20 63 in. 120 lb 2009

94-3256 21 67 in. 150 lb 2008

69-4781 30 65 in. 145 lb 2010

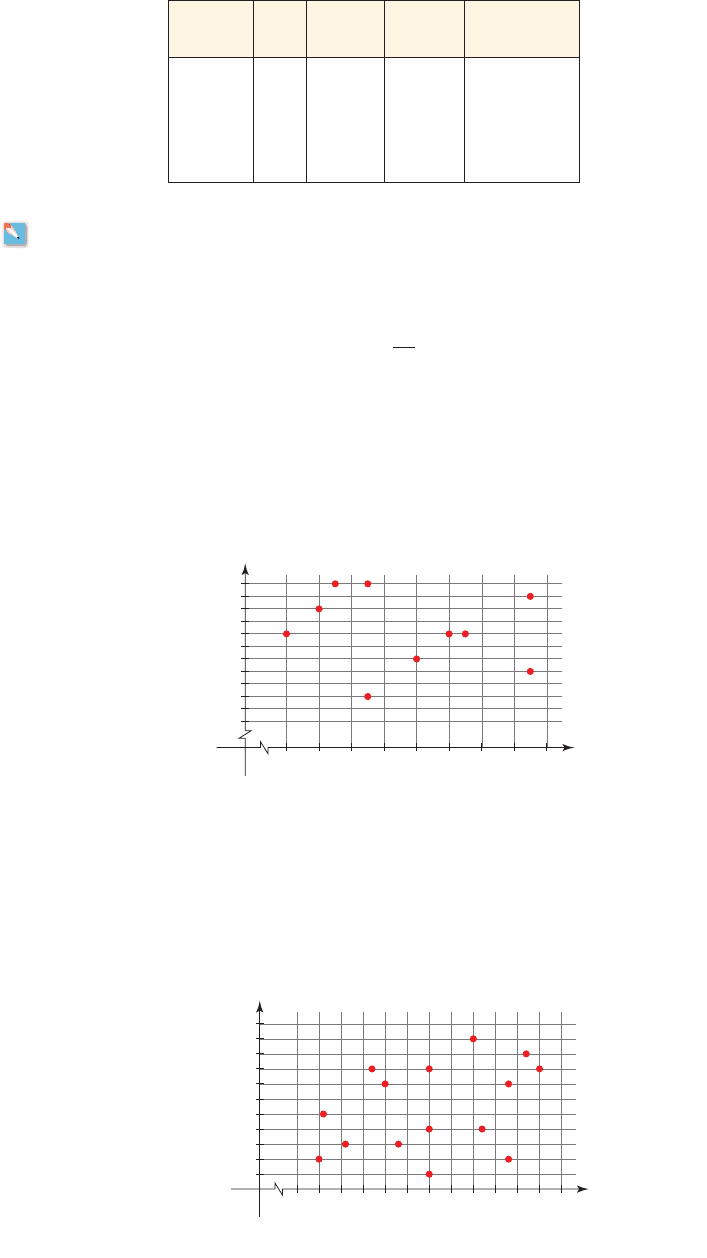
63. Body Mass Index During the last two decades the prevalence of obesity has

increased considerably in the United States, despite the popularity of diets and health

clubs. A health survey conducted over the course of forty years (1963–2003) used the

Body Mass Index (BMI) to measure obesity. The BMI is defined by the formula

where W is the weight in kilograms and H is the height in meters. The survey found that

over this 40-year period the average BMI of adults increased from 25 to 28. The graph

displays the height (in inches) and BMI of several of the subjects in the survey.

(a) Make a table of the ordered pairs in the relation given by the graph.

(b) List the ordered pairs with input 65.

BMI =

6260 6664 68

Hei

ht (in.)

7270 74 76

BMI

64. Restaurant Survey A restaurant in Rolla, Missouri, surveys its customers to help

improve the service. The graph shows some of the survey data. Displayed are the ages of

the customers surveyed and the numbers of times per month they eat in the restaurant.

(a) Make a table of the ordered pairs in the relation given by the graph.

(b) List the ordered pair(s) whose input is 50 and the ordered pair(s) with input 72.

20 30 40

50 60 70 80

Times per

month at

restaurant

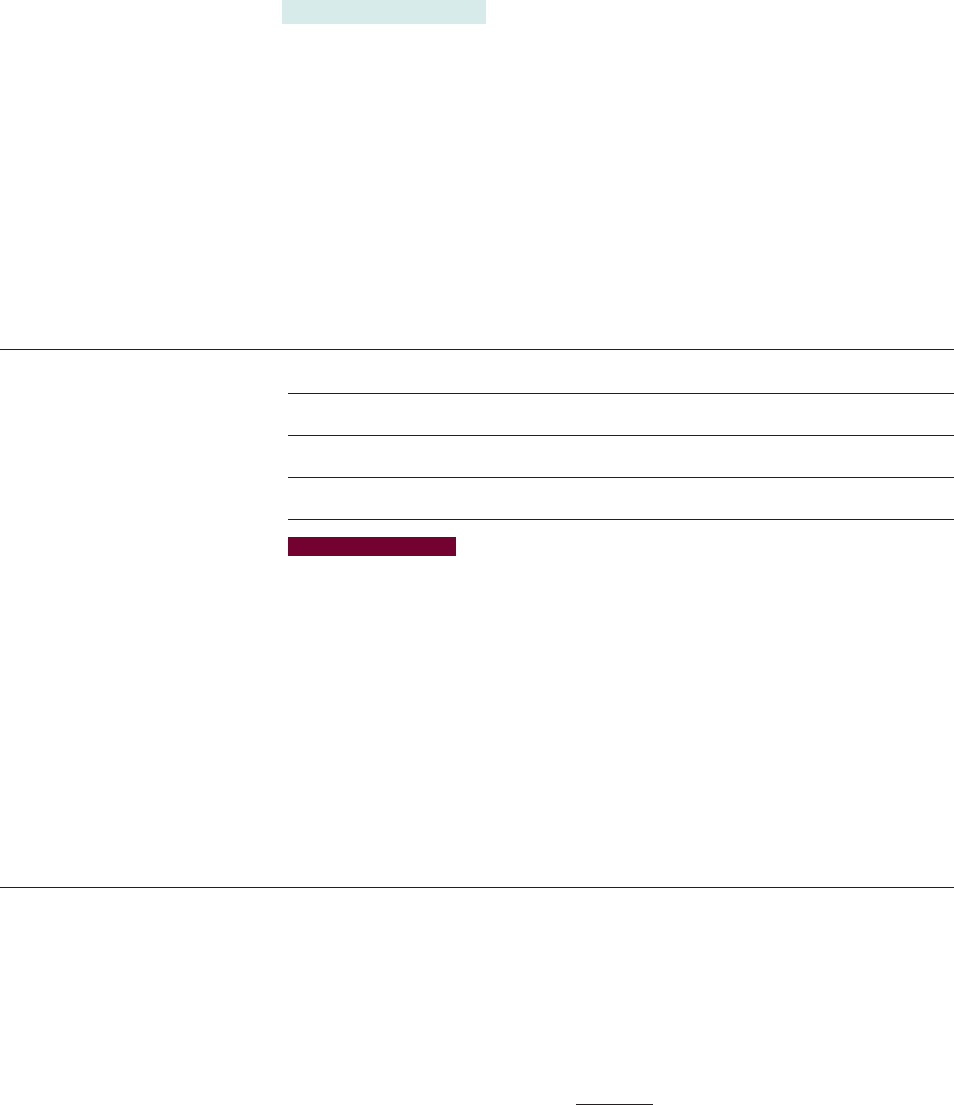
52 CHAPTER 1

■

Data, Functions, and Models

65. Algebra and Alcohol The first two columns of the table in the Prologue (page P2)

give the alcohol concentration at different times following the consumption of 15 mL of

alcohol.

(a) Do these data define the alcohol concentration as a function of time?

(b) Confirm your answer to part (a) by using the scatter plot of the data given in

Exercise 47 of Section 1.2.

alcohol concentration in a person’s blood at different times must define a

function.

1.5 Function Notation: The Concept of Function as a Rule

■

Function Notation

■

Evaluating Functions—Net Change

■

The Domain of a Function

■

Piecewise Defined Functions

IN THIS SECTION… we introduce function notation. This notation associates each

input value with its output and, at the same time, describes the rule that relates the

input and output. This notation is immensely useful and will be used throughout this

book.

Recall from Section 1.4 that a function is a relation in which each input gives ex-

actly one output. In real-world applications of functions we need to know how the

output is obtained from the input. In other words, we need to know the rule or

process that acts on the input to produce the corresponding output. So we can de-

fine a function as the rule that relates the input to the output. Viewing a function in

this way leads to a new and very useful notation for expressing functions, which we

study in this section.

■ Function Notation

A function is a relation between two changing quantities. Our goal is to discover the

rule that relates these changing quantities. To describe such a rule symbolically, we

use function notation. In this notation we give the function a name. If we use the

letter f for the name of the function (or rule), then starting with an input and apply-

ing the rule f, we get the desired output.

We express this process as an equation by writing

Note that in this notation the letter f stands for a rule, not a number.

1input2= output

input

________

Apply the rule f

output

We previously used letters such as

x, y, a, b, . . . , to represent numbers;

here we use the letter f to represent

a rule.

SECTION 1.5

■

Function Notation: The Concept of Function as a Rule 53

A function f is a rule that assigns to each input exactly one output. If we

write x for the input and y for the output, then we use the following notation

to describe f :

f 1x 2= y

Function Input Output

The symbol is read “f of x” or “f at x” and is called the value of f at x or the im-

age of x under f. This notation emphasizes the dependence of the output on the cor-

responding input—namely, the output is the result of applying the rule f to the

input x:

The following examples illustrate the meaning of function notation.

x S f 1x2

f 1x2

f 1x 2

Function Notation

example

Function Notation

Consider the function .

(a) What is the name of the function?

(b) What letter represents the input? What is the output?

(d) Find . What does represent?

Solution

(a) The name of the function is f.

(b) The input is x, and the output is 8x.

(d) . So 16 is the value of the function at 2.

■ NOW TRY EXERCISE 9 ■

f 12 2= 8 ⴢ 2 = 16

f 12 2f 12 2

f 1x 2= 8x

example

Writing Function Notation

Express the given rule in function notation.

(a) “Multiply by 2, then add 5.”

(b) “Add 3, then square.”

Solution

(a) First we need to choose a letter to represent this rule. So let stand for the rule

“Multiply by 2, then add 5.” Then for any input x, multiplying by 2 gives 2x,

then adding 5 gives . Thus we can write

Note that the input is the number x and the corresponding output is the number

.2x + 5

g1x 2= 2x + 5

2x + 5