Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

1.7 Working with Functions:

Getting Information from the Graph

■

Reading the Graph of a Function

■

Domain and Range from a Graph

■

Increasing and Decreasing Functions

■

Local Maximum and Minimum Values

IN THIS SECTION... we use the graph of a function to get information about the

function, including where the values of the function increase or decrease and where the

maximum or minimum value(s) of the function occur.

GET READY... by reviewing interval notation in Algebra Toolkit A.2. Test your skill in

working with interval notation by doing the Algebra Checkpoint at the end of this

section.

The graph of a function allows us to “see” the behavior, or life history, of the func-

tion. For example, we can see from the graph of a function the highest or lowest value

of the function or whether the values of the function are rising or falling. So if a func-

tion represents cost, the lowest point on its graph tells where the minimum cost oc-

curs. If a function represents profit, its graph can tell us where profit is increasing or

decreasing. In this section we examine how to obtain these and other types of infor-

mation from the graph of a function.

■ Reading the Graph of a Function

If a function models a real-world situation, such as the weight of a person, its graph

is usually easy to interpret. For example, suppose the weight of Mr. Hector (in

pounds) is given by the function W, where the independent variable x is his age in

years. So

“weight of Mr. Hector at age x”

The graph of the function W in Figure 1 gives a visual representation of how his

weight has changed over time. Note that Mr. Hector’s weight at age x is the

height of the graph above the point x.

W 1x2

W 1x2=

200

100

120

140

160

180

10 20 30 40 50 60 70

W(30)=150

W(10)=80

figure 1 Graph of Mr. Hector’s weight

74 CHAPTER 1

■

Data, Functions, and Models

SECTION 1.7

■

Working with Functions: Getting Information from the Graph 75

example

Verbal Description from a Graph

Answer the following questions about the function W graphed in Figure 1.

(a) What was Mr. Hector’s weight at age 10? At age 30?

(b) Did his weight increase or decrease between the ages of 40 and 50? Between

the ages of 50 and 70?

(d) What was his minimum weight between the ages of 30 and 50?

(e) What was his maximum weight between the ages of 30 and 70?

(f) What is the net change in his weight from the age of 30 to 50?

Solution

(a) His weight at age 10 is W(10). The value of W(10) is the height of the graph

above the x-value 10. From the graph we see that . Similarly,

from the graph, .

(b) From the graph we see that the values of the function W were increasing

between the x-values 40 and 50, so Mr. Hector’s weight was increasing during

that period. However, the graph indicates that his weight was decreasing

between the ages of 50 and 70.

ages of 20 and 30. He maintained his weight at 150 lb during that period.

(d) From the graph we see that the minimum value that W achieves between the

x-values of 30 and 50 is 130. So Mr. Hector’s minimum weight during that

period was 130 lb.

(e) From the graph we see that the maximum value that W achieves between the

ages of 30 and 70 is 200 lbs. So Mr. Hector’s maximum weight during that

period was 200 lb.

(f) From the graph we see that at age 30 Mr. Hector weighed 150 lb and at age 50

he weighed 200 lb. We have , so the net

change in his weight between those two ages is 50 lb.

■ NOW TRY EXERCISE 41 ■

A complete graph of a function contains all the information about the function,

because the graph tells us which input values correspond to which output values. To

analyze the graph of a function, we must keep in mind that the height of the graph is

the value of the function. So we can read the values of a function from its graph.

W1502- W1302= 200 - 150 = 50

W 1302= 150

W 1102= 80

example

Finding the Values of a Function from a Graph

The function T graphed in Figure 2 gives the temperature between noon and 6:00 P.M.

at a certain weather station.

(a) Find T(1), T(3), and T(5).

(b) Which is larger, T(2) or T(4)?

(d) Find the values of x for which .

(e) Find the net change in temperature between 3:00 and 5:00 P.M.

T1x 2Ú 25

T1x 2= 25

T (*F)

123456

figure 2

Interval notation is reviewed

in Algebra Toolkit A.2,

page T7.

example

Where Graphs of Functions Meet

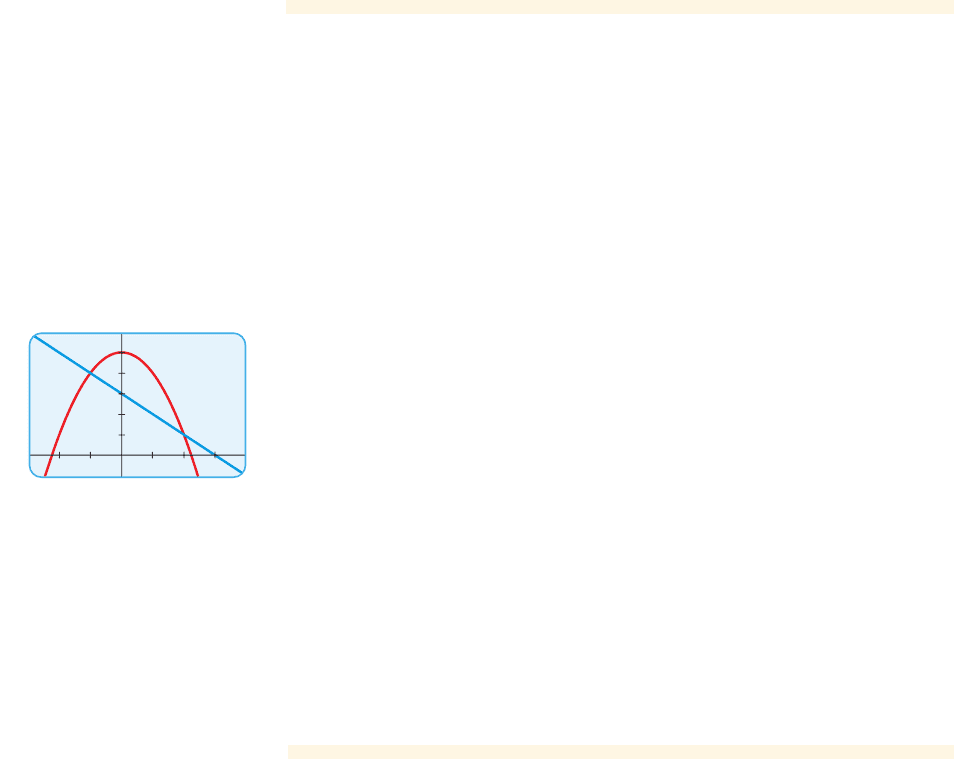
Use a graphing calculator to draw graphs of the functions and

in the same viewing rectangle.

(a) Find the value(s) of x for which .

(b) Find the values of x for which .

Solution

We graph the equations

in the same viewing rectangle in Figure 3.

(a) Recall that the value of a function is the height of the graph. So at

the x-values where the graphs of f and meet. From Figure 3 we see that the

graphs meet when x is and when x is 2. So when x is and

when x is 2.

(b) We need to find the x-values where . These are the x-values where

the graph of f is above the graph of . From Figure 3 we see that this happens

for x between and 2. So for x in the interval .

the graph of f is below the graph of . From Figure 3 we see that this happens

for x strictly less than and x strictly bigger than 2, that is, and

. (We don’t include the points and 2 because of the strict inequality.)

So for x in the intervals and .

■ NOW TRY EXERCISE 11 ■

12, q 21- q, - 12f 1x 26 g1x2

- 1x 7 2

x 6-1- 1

f 1x 26 g1x2

3- 1, 24f 1x 2Ú g1x2- 1

f 1x 2Ú g1x2

- 1f 1x 2= g1x2- 1

f 1x 2= g1x2

= 5 - x

andy

= 3 - x

f 1x 26 g1x2

f 1x 2Ú g1x2

f 1x 2= g1x2

g1x 2= 3 - x

f 1x2= 5 - x

76 CHAPTER 1

■

Data, Functions, and Models

Solution

(a) is the temperature at 1:00 P.M. It is represented by the height of the graph

above the x-axis at the x-value 1. Thus . Similarly, and

(b) Since the graph is higher at the x-value 2 than at the x-value 4, it follows that

is greater than .

x is 1 and when x is 4.

(d) The graph is higher than 25 for x between 1 and 4. So for all

x-values in the interval [1,4].

(e) From the graph we know that is 20 and is 30. We have

So the net change in temperature is .

■ NOW TRY EXERCISES 7 AND 43 ■

- 10°F

=-10

T152- T132= 20 - 30

T 132T 152

T 1x2Ú 25

T 1x2= 25

T14 2T122

T 152= 20

T 132= 30T 112= 25

T 112

figure 3 Graphs of f and g

SECTION 1.7

■

Working with Functions: Getting Information from the Graph 77

■ Domain and Range from a Graph

Recall from Section 1.4 that for a function of the form we have the following:y = f 1x2

Domain Range

Inputs Outputs

Independent variable Dependent variable

x-values y-values

The domain and range of a function f are represented in the graph of the

function as shown in the figure.

Range

Domain

So since the graph of f consists of the ordered pairs , the domain and range of

the function can be obtained from the graph as follows.

Domain and Range from a Graph

1x, y 2

For the function W graphed in Figure 1 on page 74, the domain is the interval

[0, 70] and the range is the interval [10, 200]. Note that the domain consists of all in-

puts (ages of Mr. Hector) and the range consists of all outputs (weights of Mr. Hector).

example

Domain and Range from a Graph

Let f be the function defined by .

(a) Use a graphing calculator to draw a graph of f.

(b) Find the domain and range of f from the graph.

Solution

(a) The graph is shown in Figure 4.

f 1x 2= 24 - x

Domain=[_2, 2]

Range=[0, 2]

figure 4

■

The function f is increasing if the values of increase as x increases.

That is, f is increasing on an interval I if whenever in I.

■

The function f is decreasing if the values of decrease as x increases.

That is, f is decreasing on an interval I if whenever in I.a 6 bf 1a27 f 1b 2

f 1x 2

a 6 bf 1a 26 f 1b2

f 1x 2

(b) From the graph we see that the domain is the interval and the range is

the interval .

■ NOW TRY EXERCISE 19 ■

30, 24

3- 2, 24

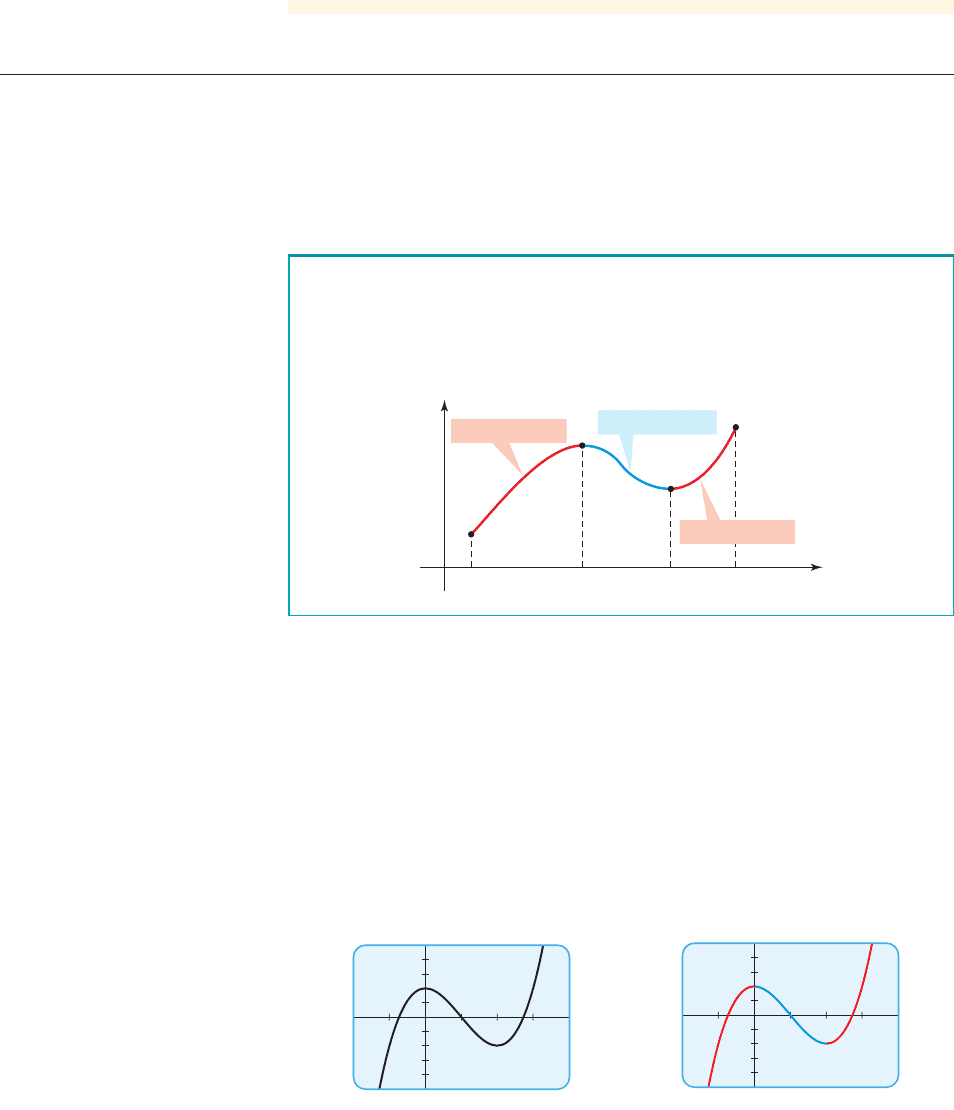
■ Increasing and Decreasing Functions

At the beginning of this section we saw that the graph of Mr. Hector’s weight rises

when his weight increases and falls when his weight decreases. In general, a func-

tion is said to be increasing when its graph rises and decreasing when its graph falls.

Increasing and Decreasing Functions

f is increasing

f is decreasing

78 CHAPTER 1

■

Data, Functions, and Models

example

Increasing and Decreasing Functions

Use a graphing calculator to draw a graph of .

(a) Find the intervals on which f is increasing.

(b) Find the intervals on which f is decreasing.

Solution

Using a graphing calculator, we draw a graph of the function f as shown in Figure 5.

(a) From the graph we see that f is increasing on and on (repre-

sented in red in Figure 6).

32, q 21- q, 04

f 1x 2= x

- 3x

+ 2

figure 5

figure 6

SECTION 1.7

■

Working with Functions: Getting Information from the Graph 79

(b) From the graph we see that f is decreasing on (represented in blue in

Figure 6).

■ NOW TRY EXERCISE 27 ■

30, 24

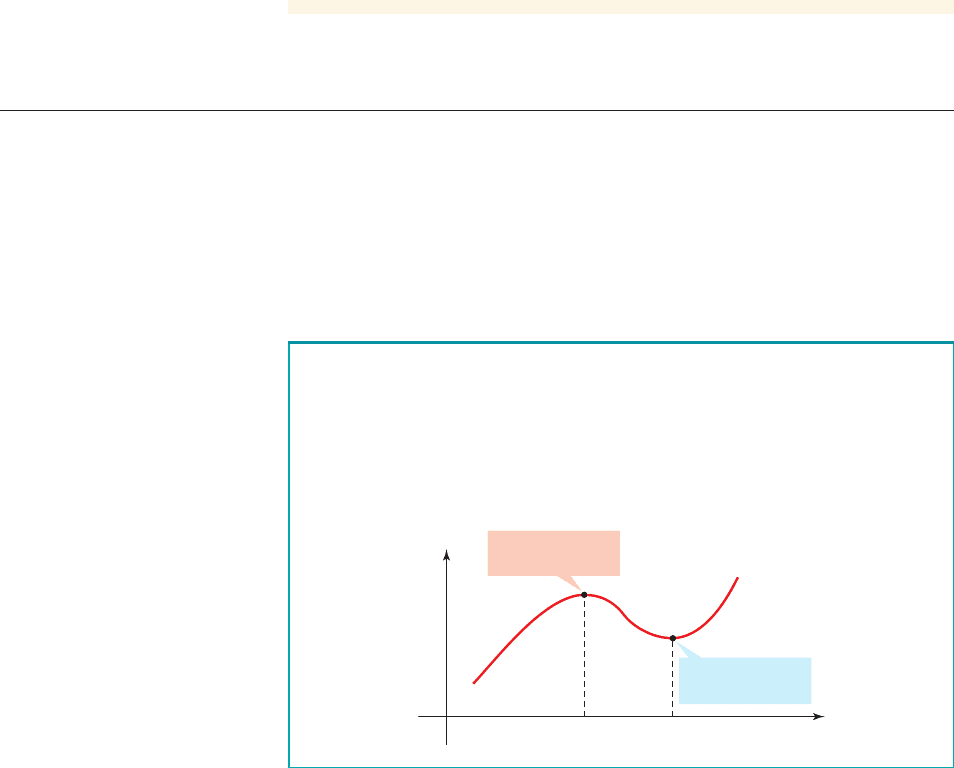
■ Local Maximum and Minimum Values

Finding the largest or smallest values of a function is important in many applications.

For example, if a function represents profit, then we are interested in its maximum

value. For a function that represents cost, we would be interested in its minimum

value. We can find these values from the graph of a function. We first define what we

mean by a local maximum or minimum.

Local Maximum and Minimum Values

The statement “ for values of x near a” means that for

all x in some open interval containing a. Similarly, the statement “ for

values of x near a” means that for all x in some open interval con-

taining a.

f 1a 2… f 1x2

f 1a2Ú f 1x 2f 1a 2Ú f 1x2

■

The function value is a local maximum value of f if

for values of x near a

■

The function value is a local minimum value of f if

for values of x near af 1a 2… f 1x2

f 1a 2

f 1a 2Ú f 1x2

f 1a 2

xba

Local maximum

value f(a)

Local minimum

value f(b)

example

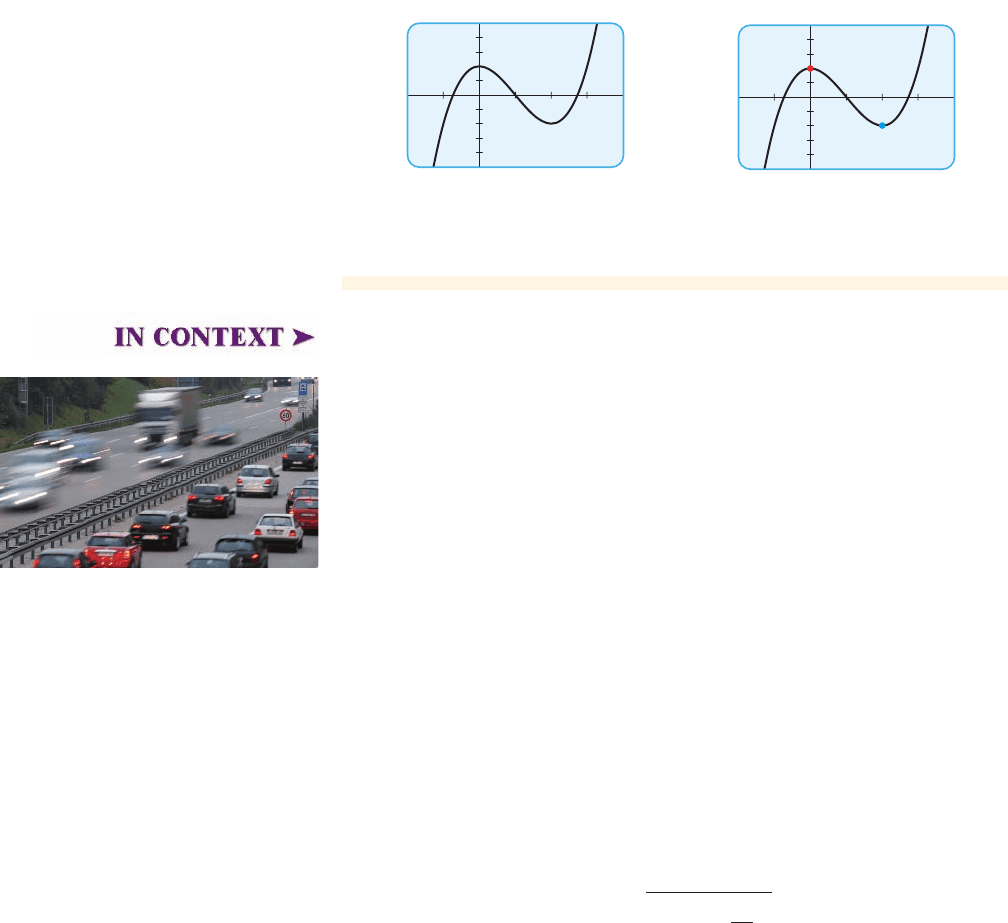
Local Maximum and Minimum Values of Functions

Find the local maximum and minimum values of .

Solution

The graph of f is shown in Figure 7 on the next page. From the graph we see that f has

a local maximum value 2 at the x-value 0. In other words, is a local maximumf 10 2= 2

f 1x2= x

- 3x

+ 2

Intervals are studied in Algebra

Toolkit A.2, page T7.

80 CHAPTER 1

■

Data, Functions, and Models

value (represented by the red dot on the graph in Figure 7). Similarly, is a

local minimum value (represented by the blue dot on the graph in Figure 8).

f 12 2=-2

■ NOW TRY EXERCISE 37 ■

Highway engineers use mathematics to study traffic patterns and relate them to

different road conditions. One feature that they are interested in is the carrying ca-

pacity of a road—that is, the maximum number of cars that can safely travel along a

certain stretch of highway. If the cars drive very slowly past a given point on the road,

only a few can pass by every minute. On the other hand, if the cars are zooming

quickly past that point, safety concerns require them to be spaced much farther apart,

so again not many can pass by every minute. Between these two extremes is an op-

timal speed at which these two competing tendencies balance to allow as many cars

as possible to drive down this stretch of road.

In the next example we use a graphing calculator to analyze the graph of a func-

tion developed by an engineer to model the carrying capacity of a highway. (See

Exploration 3 on page 560 to learn how this model is obtained.) The model assumes

that all drivers observe the “safe following distance” guidelines; in reality, the ma-

jority of drivers do not, resulting in traffic congestion and accidents.

figure 7

figure 8

IN CONTEXT ➤

example

Highway Engineering

A highway engineer develops a formula to estimate the number of cars that can

safely travel a particular highway at a given speed. She assumes that each car is

17 feet long, travels at a speed of x mi/h, and follows the car in front of it at the

safe following distance for that speed. She finds that the number N of cars that

can pass a given point per minute is modeled by the function

Graph the function in the viewing rectangle [0, 100] by [0, 60].

(a) Where is the function N increasing? Decreasing?

(b) What is the local maximum value of N? At what x-value does this local

maximum occur?

N 1x2=

88x

17 + 17 a

Manfred Steinbach/Shutterstock.com 2009

SECTION 1.7

■

Working with Functions: Getting Information from the Graph 81

Solution

The graph is shown in Figure 9.

(a) From the graph we see that the function N is increasing on and

decreasing on .

(b) From the graph we see that N has a local maximum value of about 52 at the

x-value 20. So the highway can accommodate more cars at about 20 mi/h than

at higher or lower speeds.

capacity of the road is achieved at 20 mi/h.

■ NOW TRY EXERCISE 49 ■

320, 1004

30, 204

100

figure 9 Highway capacity at

speed x

Test your skill in working with interval notation. Review this topic in

Algebra

Toolkit A.2

on page T7.

1–4 A set of numbers is given.

(a) Give a verbal description of the set.

(b) Express the set in interval notation.

5–8 An interval is given.

(a) Give a verbal description of the interval.

(b) Express the interval in set-builder notation.

5. (2, 6) 6. 7. 8.

9–12 The graph of an interval is given.

(a) Give a verbal description of the interval.

(b) Express the interval in set-builder notation.

9. 10.

11. 12.

3- 1, q 21- q, 221- 4, 34

5x 冨 x Ú 06

5x 冨 - 10 6 x 6-36

5x 冨 - 3 … x 6 26

5x 冨1 … x … 46

_1 1

_3 0

1.7 Exercises

CONCEPTS

Fundamentals

1–4 ■ These exercises refer to the graph of the function f shown at the left.

1. To find a function value from the graph of f, we find the height of the graph above

the x-axis at x ⫽

_______. From the graph of f we see that _______.

2. The domain of the function f is all the _______-values of the points on its graph, and

the range is all the corresponding

_______-values. From the graph we see that the

domain of f is the interval

_______ and the range of f is the interval _______.

3. (a) If f is increasing on an interval, then the y-values of the points on the graph

_______ (increase/decrease) as the x-values increase. From the graph we see that f

is increasing on the intervals

_______ and _______.

(b) If f is decreasing on an interval, then the y-values of the points on the graph

_______ (increase/decrease) as the x-values increase. From the graph we see that f

is decreasing on the intervals

_______ and _______.

4. (a) A function value is a local maximum value of f if is the

_______ value

of f on some interval containing a. From the graph we see that one local maximum

value of f is

_______ and that this value occurs when x is _______.

(b) A function value is a local minimum value of f if is the

_______ value

of f on some interval containing a. From the graph we see that one local minimum

value of f is

_______ and that this value occurs when x is _______.

Think About It

5. In Example 7 we saw a real-world situation in which it is important to find the

maximum value of a function. Name several other everyday situations in which a

maximum or minimum is important.

6. Draw a graph of a function f that is defined for all real numbers and that satisfies the

following conditions: f is always decreasing and for all x.

7. The graph of a function h is given.

(a) Find , and .

(b) Find the domain and range of h.

(d) Find the values of x for which .

(e) Find the net change in the value of h when

x changes from .

8. The graph of a function is given.

(a) Find , and .

(b) Find the domain and range of .

(d) Find the values of x for which .

(e) Find the net change in the value of when

x changes from 2 to 7.

g1x 27 4

g1x 2= 4

g172g1- 22, g10 2

- 2 to 4

h 1x 2… 3

h 1x 2= 3

h 13 2

h 1- 22, h 102, h 122

f 1x 27 0

f 1a 2f 1a 2

f 132=

f 1a 2

SKILLS

82 CHAPTER 1

■

Data, Functions, and Models

3_3

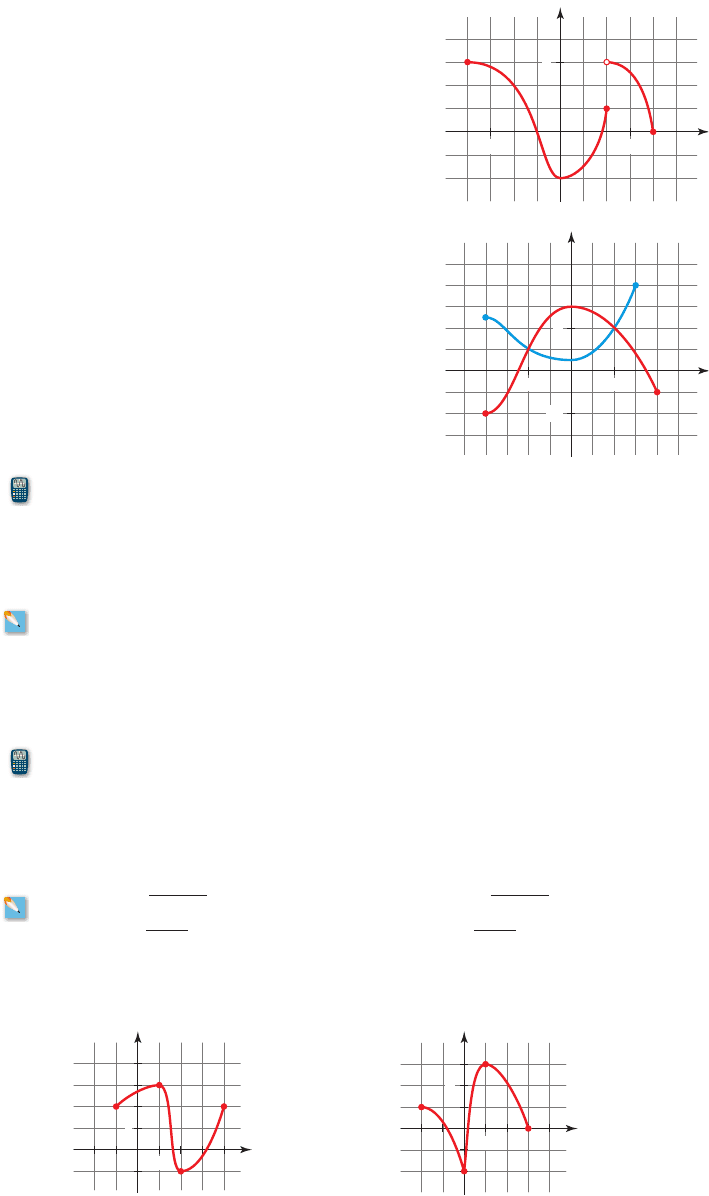
SECTION 1.7

■

Working with Functions: Getting Information from the Graph 83

9. The graph of a function is given.

(a) Find , , , , and .

(b) Find the domain and range of .

10. Graphs of the functions f and are given.

(a) Which is larger, ?

(b) Which is larger, ?

11–14

■ Graph the functions f and with a graphing calculator. Use the graphs to find the

indicated values or intervals; state your answer correct to two decimal places.

(a) Find the value(s) of x for which .

(b) Find the values of x for which .

11.

12.

13.

14.

15–22

■ A function f is given.

(a) Use a graphing calculator to draw the graph of f.

(b) Find the domain and range of f from the graph.

15. 16.

17. 18.

19. 20.

21. 22.

23–26

■ The graph of a function is given. Determine the intervals on which the function is

(a) increasing and (b) decreasing.

23. 24.

f 1x 2= 1x + 2

f 1x 2= 1x - 1

f 1x 2=-225 - x

f 1x 2= 216 - x

f 1x 2= 4 - x

f 1x 2=-x

f 1x 2= 4f 1x 2= x - 1

f 1x 2= 1 - x

,g1x 2= x

- 2x - 1

f 1x 2= 2x

+ 3,g1x2=-x

+ 3x + 5

f 1x 2=-2x

+ 3x - 1,g1x2= 3x - 9

f 1x 2= x

- 5x + 1,g1x2=-3x + 4

f 1x 26 g1x 2

f 1x 2Ú g1x 2

f 1x 2= g1x 2

f 1- 32 or g1- 32

f 102 or g102

g142g122g102g1- 22g1- 42

3_3

2_2