Stewart J. College Algebra: Concepts and Contexts
Подождите немного. Документ загружается.

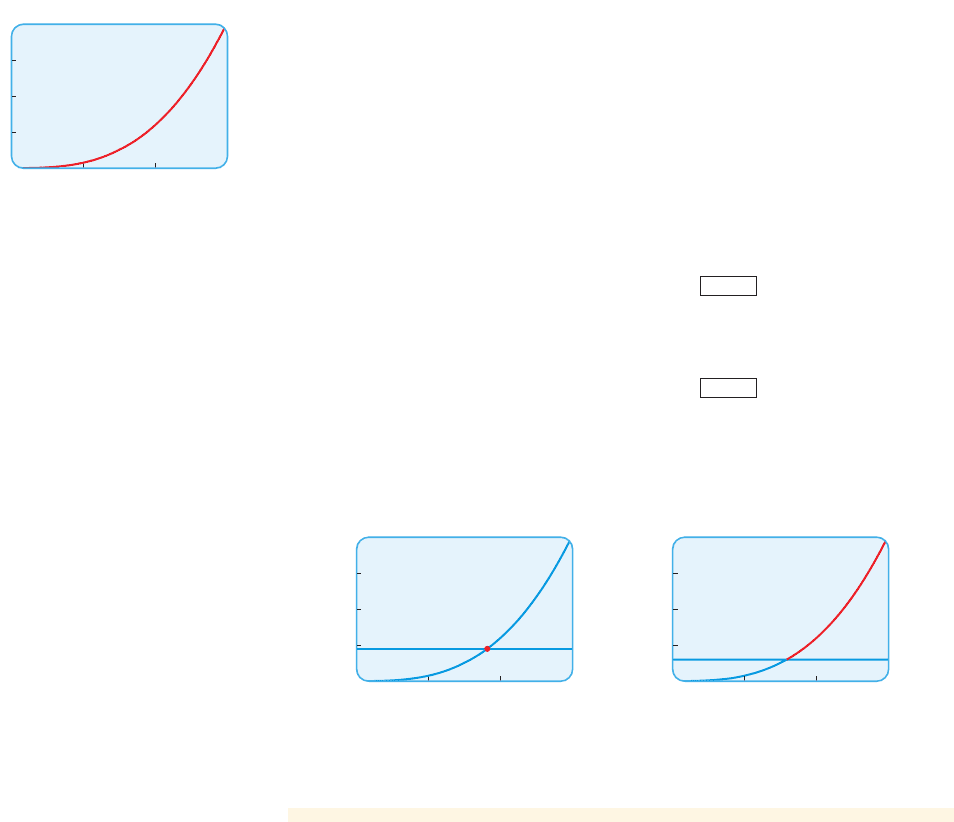
The model is the function that gives the volume of the box in terms of the
depth x.
So the volume of the box is modeled by the function . The function
is graphed in Figure 1.
(b) If the depth is 1.5 in., the volume is .
(c) We need to solve the equation . The function and the
line are graphed in Figure 2. Using the feature on a graphing
calculator, we find that the two graphs intersect when , so the volume
is when the depth is about 1.82 in.
(d) We need to solve the inequality . The function and the
line are graphed in Figure 3. Using the feature on a graphing
calculator, we find that the two graphs intersect when and hence that
when (as shown in red in Figure 3). So the volume is
greater than when the depth is greater than 1.59 in.60 in
3
x Ú 1.59V1x 2Ú 60
x L 1.59
TRACE
y = 60
V1x 2= 15x
3
V1x 2Ú 60
90 in
3
x L 1.82
TRACE
y = 90
V1x 2= 15x
3
V1x 2= 90
V11.5 2= 1511.52
3
= 50.625 in
3
V
V1x 2= 15x
3
V1x2= 15x
3
V1x2= x
#
3x
#
5x
volume = depth * width * height
V
0
400
3
figure 1 V1x 2= 15x
3
94 CHAPTER 1
■
Data, Functions, and Models
0
400
3
15x£=90
y=15x£
y=90
figure 2
0
400
3
15x
£≥
60
y=15x£
y=60
figure 3
example
5
Fencing a Garden
A gardener has 140 ft of fencing to fence a rectangular vegetable garden.
(a) Find a function that models the area of the garden she can fence.
(b) For what range of widths is the area greater than ?
(c) Can she fence a garden with area ?
(d) Find the dimensions of the largest area she can fence.
1250 ft
2
825 ft
2
■ NOW TRY EXERCISE 27 ■
In the next example we find a model that allows us to maximize the area that can
be enclosed by a fence of fixed length.
We can also solve this equation
algebraically. (See Algebra
Toolkit C.1, page T47.)
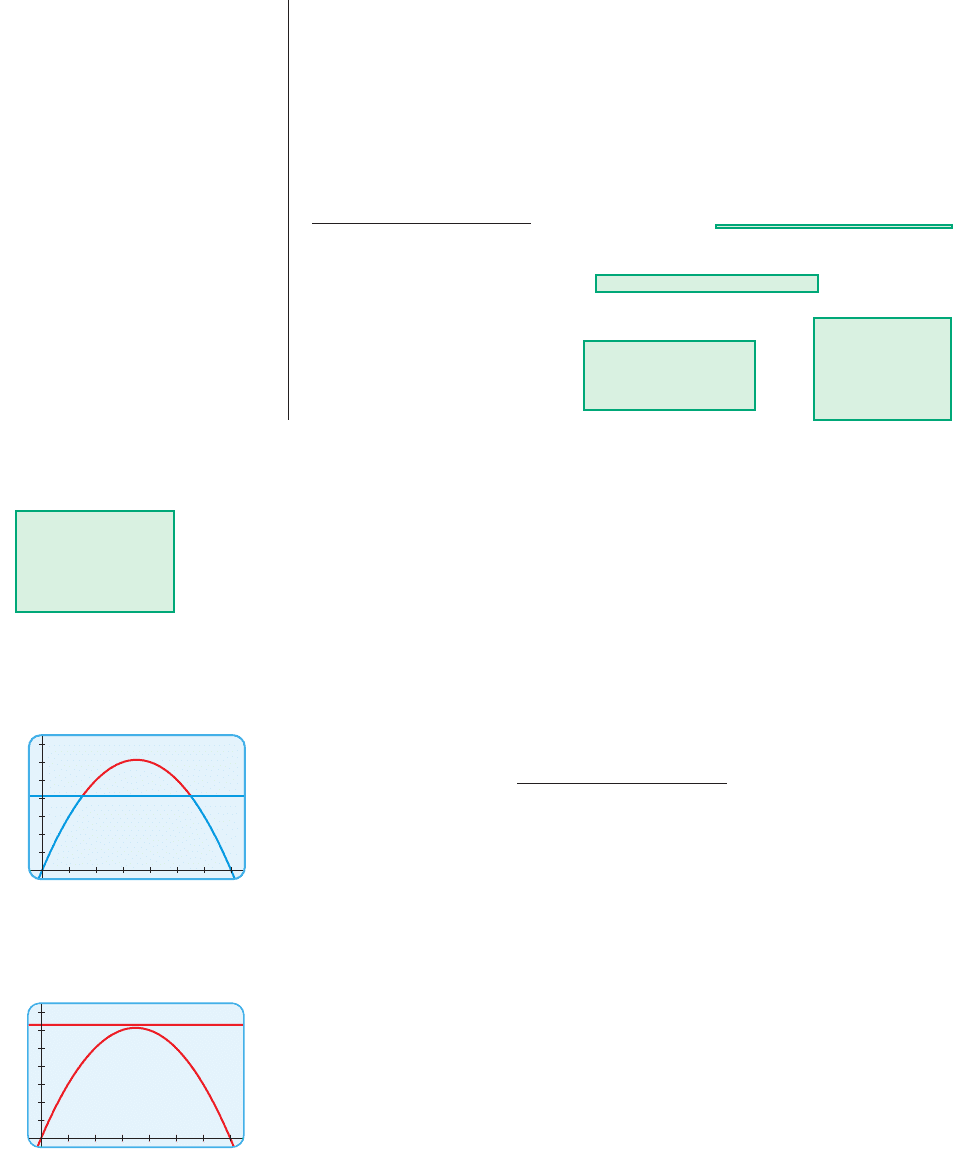
Thinking About the Problem
If the gardener fences a plot with width 10 ft, then the length must be 60 ft, be-
cause . So the area is
The table shows various choices for fencing the garden. We see that as the width
increases, the area of the garden first increases and then decreases.
A = width * length = 10
#
60 = 600 ft
2
10 + 10 + 60 + 60 = 140
Solution
(a) The model that we want is a function that gives the area she can fence. So we
begin by recalling the formula for the area of a rectangle.
There are two varying quantities: width and length. Because the function we
want depends on only one variable, we let
Then we must express the length in terms of x. The perimeter is fixed at 140 ft,
so the length is determined once we choose the width. If we let the length be l,
as in Figure 4, then , so . We summarize these facts.l = 70 - x2x + 2l = 140
x = width of the garden
area = width * length
69 ft
1 ft
5 ft
20 ft
30 ft
65 ft
50 ft
40 ft
SECTION 1.8
■
Working with Functions: Modeling Real-World Relationships 95
Width Length Area
10 60 600
20 50 1000
30 40 1200
40 30 1200
50 20 1000
60 10 600
In Words In Algebra
Width x
Length
70 - x
x
l
x
l
figure 4
The model we want is the function A that gives the area of the garden for any
width x.
The area that she can fence is modeled by the function .
(b) We need to solve the inequality . To solve graphically, we graph
and in the same viewing rectangle (see Figure 5). We
see that the graph of A is higher than the graph of for .
(c) From Figure 6 we see that the graph of A(x) always lies below the line
, so an area of is never attained. Hence, the gardener cannot
fence an area of .1250 ft
2
1250 ft
2
y = 1250
15 … x … 55y = 825
y = 825y = 70x - x
2
A1x 2Ú 825
A1x 2= 70x - x
2
A1x2= 70x - x
2
A1x2= x170 - x2
area = width * length
1500
_100
_5 75
y=70x-≈
y=825
figure 5
1500
_100
_5 75
y=70x-≈
y=1250
figure 6
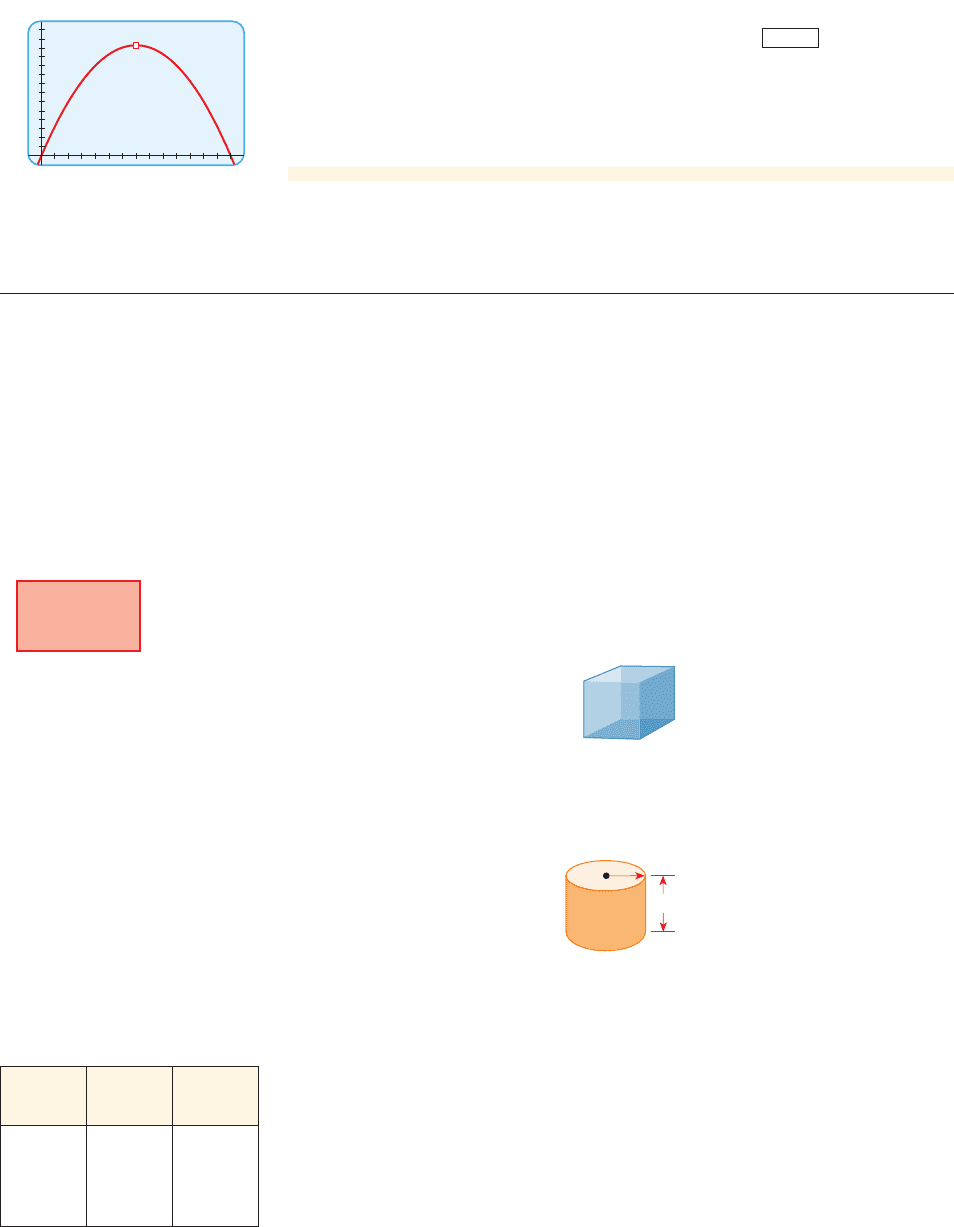
x
2x
x
First
number
Second
number
Product
1 18
18
2 17
34
3 16
48
o o o
1500
_100
_5
75
y=70x-x™
(35, 1225)
figure 7
96 CHAPTER 1
■
Data, Functions, and Models
1.8 Exercises
SKILLS
1–6 ■ Find a function that models the quantity described.
1. The number N of days in w weeks.
2. The number N of cents in q quarters.
3. The sum S of two consecutive integers, the first integer being n.
4. The sum S of a number n and its square.
5. The product P of a number x and twice that number.
6. The product P of a number y and one and a half times that number.
7–12
■ Find a function that models the quantity described. You may need to consult the
formulas for area and volume listed on the inside back cover of this book.
7. The area A of a rectangle whose length is 4 ft more than its width x.
8. The perimeter P of a rectangle whose length is 4 ft more than its width x.
9. The volume of a cube of side x.V
4+x
x
(d) We need to find where the maximum value of the function
occurs. The function is graphed in Figure 7. Using the feature on a
graphing calculator, we find that the function achieves its maximum value at
So the maximum area that she can fence occurs when the garden’s
width is 35 ft and its length is ft. Then the maximum area is
.35 * 35 = 1225 ft
2
70 - 35 = 35
x = 35.
TRACE
A1x 2= 70x - x
2
■ NOW TRY EXERCISE 29 ■
10. The volume B of a box with a square base of side x and height 2x.
11. The area A of a triangle whose base is twice its height h.
12. The volume of a cylindrical can whose height is twice its radius, as shown in the figure.V
13–16
■ In these problems you find a function that models a real-life situation and then use
the graphing calculator to graph the model and answer questions about the
situation. Exercise 13 shows the steps involved in solving these problems.
13. Consider the following problem: Find two numbers whose sum is 19 and whose product
is as large as possible.
(a) Experiment with the problem by making a table like the one in the margin, showing
the product of different pairs of numbers that add up to 19. On the basis of the
evidence in your table, estimate the answer to the problem.
(b) Find a function f that models the product in terms of one of the numbers x.
(c) Use a graphing calculator to graph the model and solve the problem. Compare with
your answer to part (a).
f 1x 2
14. Find two positive numbers whose sum is 100 and the sum of whose squares is a
minimum.
15. Find two numbers whose sum is and whose product is a maximum.
16. Among all rectangles that have a perimeter of 20 ft, find the dimensions of the one with
the largest area.
- 24
SECTION 1.8
■
Working with Functions: Modeling Real-World Relationships 97
CONTEXTS
17. Tee Shirt Cost A tee shirt company makes tee shirts with school logos. The company
charges a fixed fee of $200 to set up the machines plus $3.50 per tee shirt.
(a) Find a function C that models the cost of purchasing x tee shirts.
(b) Use the model to find the cost of purchasing 600 tee shirts.
18. Rental Cost A flea market charges vendors a fixed fee of $60 a month plus 75 cents
per square foot for renting a space.
(a) Find a function C that models the cost for one month’s rental of a space with area
x square feet.
(b) Use the model to find the cost of one month’s rental of a space with area 150 square
feet.
19. Gas Cost The cost of driving a car depends on the number of miles driven and the gas
mileage of the car. Kristi owns a Honda Accord that gets 30 miles to the gallon.
(a) Find a function C that models the cost of driving Kristi’s car x miles if the cost of
gas is $3.20 per gallon.
(b) Use the model to find the cost of driving Kristi’s car 500 miles.
(c) Kristi’s budget for gas is $250 a month. Use the model to find the number of miles
Kristi can drive each month without exceeding her monthly gas budget.
20. Exchange Rate Jason travels from his home in Connecticut to Germany to visit his
grandparents. At the time the euro/dollar exchange rate was 1.5532, which means that
each euro cost 1.5532 U.S. dollars.
(a) Find a function A that models the number of U.S. dollars required to purchase x
euros.
(b) Jason bought a vase in Hamburg for his grandmother for 153.00 euros. Use the
model to find the price of the vase in U.S. dollars.
(c) The day before returning home, Jason found that he had 200 U.S. dollars worth of
traveler’s checks left. He decided to convert these to euros to spend in Germany.
Use the model to find how many euros he received for his $200.
21. Cost of Wedding Sherri and Jonathan are getting married. They have a budget of
$5000. They are planning the reception and choose a reception hall that costs $700, a
DJ that costs $300, a caterer that charges $18.50 a plate, and a wedding cake that costs
$1.50 per guest.
(a) Complete the table for the cost of the reception for the given number of guests.
Number
of guests
Cost
of hall
Cost
of DJ
Cost of
caterer
Cost of
wedding cake
Total cost of
reception
10
$700 $300 $185 $15 $1200
20
30
40
50
(b) Find a function C that models the cost of the reception when x guests attend.
(c) Determine how much the reception would cost if 75 people attend; that is, find the
value of C(75).
(d) Determine how many people can attend the reception if Sherri and Jonathan spend
their total budget of $5000; that is, find the value of x when
22. Cost of Reception A business group is hosting a reception for local dignitaries. The
group chooses to hold the event at an exclusive country club that charges a $2000 rental
fee. In addition, they choose a caterer that charges $21.00 a plate, gifts that cost $5.00
per guest, and decorations that cost $1500.
(a) Find a function C that models the cost of hosting the reception when x guests
attend.
(b) Determine how much the reception would cost if 200 people attend; that is, find the
value of C(200).
(c) Determine how many people can attend the reception if the business group’s budget
for the reception is $10,000.
23. Discounts An art supply store has a sale on picture frames, advertising “Buy One,
Get the 2nd for One Penny.”
(a) Complete the table for the total cost of purchasing the indicated number of picture
frames.
C1x 2= 5000.
Number of
frames
Number that
are $10 each
Number that are
1 cent each
Total
cost
2
1 1 $10.01
4
6
8
10
(b) Find a function C that models the cost of purchasing x frames that normally cost
$10 each. (Assume that x is an even number.)
(c) Aaron needs 20 picture frames for all his childhood pictures. Use the model to find
Aaron’s cost of getting these frames, if all the frames he gets normally cost $10
each.
24. Discounts A competitor of the art supply store in Exercise 23 offers a 35% discount
on all frames.
(a) Find a function C that models the cost of purchasing x frames that normally cost
$10 each.
(b) Use the model to find Aaron’s cost of getting 20 frames with the competitor’s sale,
if all the frames normally cost $10. Is this a better deal than the one in Exercise 23?
25. Volume of Cereal Box A breakfast cereal manufacturer packages cereal in boxes that
are 4 inches taller than they are wide and always have a depth of 3 inches.
(a) Complete the table for the dimensions and volume of a cereal box.
98 CHAPTER 1
■
Data, Functions, and Models
SECTION 1.8
■
Working with Functions: Modeling Real-World Relationships 99
(b) Find a function that models the volume of a cereal box that is x inches wide.
(c) Use the model to find the volume of a cereal box that is 10 in. wide.
(d) The manufacturer makes a box of wheat bran cereal with a volume of 300 Use
a graphing calculator to find the width of this box, as in Example 4.
26. Profit of Fund-Raiser A land conservancy in California organizes several fund-
raisers every year. One year, the board of directors for the conservancy suggests raising
money by offering tours of their nature preserve for a price of $50 per person. They
believe they can attract more people if they offer group discounts of $1 per person. So if
two people go on the tour, they will charge $49 per person (for a total of $98); if three
people go on the tour, they will charge $48 per person (for a total of $144), and so on.
(a) Complete the table for the revenue from a tour with the given number of people.
in
3
.
V
Number of
people in tour
Price per
person
Revenue
1
$50 $50
2
$49 $98
3
$48 $144
4
5
6
(b) Find a function R that models the revenue when x people take the tour.
(c) Find the revenue if 10 people go on a tour; that is, find the value of R(10).
(d) Use a graphing calculator to find the number of people that must go on the tour in
order for the conservancy to raise $650.
27. Volume of a Container A Florida orange grower ships orange juice in rectangular
plastic containers that have square ends and are one and a half times as long as they are
wide. (See the figure.)
(a) Find a function that models the volume of a container of width x.
(b) Use the model to find the volume of a container of width 10 in.
(c) Graph the function . Use the graph to find the width of the plastic container that
has a volume of .
(d) Use the graph from part (c) to find the widths for which the container has volume
greater than . Express your answer in interval notation.450 in
3
315 in
3
V
V
1.5x
x
x
Width
(in.)
Height
(in.)
Depth
(in.)
Volume
(in
3
)
3
7 3 63
4
5
6
7
28. Volume of Box A shipping company uses boxes that have square ends and are twice
as long as they are wide. (See the figure.)
(a) Find a function S that models the surface area of a box whose square end is x in.
wide.
(b) The company uses boxes that are 8 in. wide to ship cans of beans. Use the model to
find the area of the material used to make each box.
(c) A box that ships a dozen cans of soup has a surface area of 330 . Graph the
function S to find the width of that box.
(d) To ensure that the boxes are strong enough to safely hold their contents, they
should have a surface area no larger than 550 . Use the graph from part (c) to
find all possible widths for the shipping box. Express your answer in interval
notation.
29. Fencing a Field Consider the following problem: A farmer has 2400 ft of fencing and
wants to fence off a rectangular field that borders a straight river. He does not need a
fence along the river (see the figure). What are the dimensions of the field of largest
area that he can fence?
(a) Experiment with the problem by drawing several diagrams illustrating the situation.
Calculate the area of each configuration, and use your results to estimate the
dimensions of the largest possible field.
(b) Find a function A that models the area of a field in terms of one of its sides x.
(c) Use a graphing calculator to find the dimensions of the field of largest area.
Compare with your answer to part (a).
30. Dividing a Pen A rancher with 750 ft of fencing wants to enclose a rectangular area
and then divide it into four pens with fencing parallel to one side of the rectangle (see
the figure).
(a) Show that the total area of the four pens is modeled by the function
(b) Use a graphing calculator to find the largest possible total area of the four pens.
31. Volume of a Box A box with an open top is to be constructed from a rectangular
piece of cardboard with dimensions 12 in. by 20 in. by cutting out equal squares of side
x at each corner and then folding up the sides (see the figure).
(a) Show that the volume of the box is modeled by the function
(b) Use a graphing calculator to find the values of x for which the volume is greater
than 200 .
(c) Use a graphing calculator to find the largest volume that such a box can have.
in
3
V1x 2= x112 - 2x 2120 - 2x2
A1x 2=
x1750 - 5x2
2
in
2
in
2
2x
x
x
x
x
A
100 CHAPTER 1
■
Data, Functions, and Models
x
y
x
x
x
xx
x
x
x
12 in.
20 in.
x
32. Area of a Box A box with an open top and a square base is to have a volume of .
(a) Find a function S that models the surface area of the box.
(b) Use a graphing calculator to find the box dimensions that minimize the amount of
material used.
12 ft
3
SECTION 1.9
■
Making and Using Formulas 101
2
1.9 Making and Using Formulas
■
What Is a Formula?
■
Finding Formulas
■
Variables with Subscripts
■
Reading and Using Formulas
IN THIS SECTION... we learn about formulas. Formulas are the fundamental way in
which algebra is used in everyday life, including in science and engineering courses. In this
section we learn to read and use formulas as well as make formulas.
We are already familiar with many formulas. For example, you certainly know the for-
mula for the area of a circle, . You may remember the formula from
your science courses; this formula relates the pressure P, volume , and temperature T
of a gas. No doubt you’ve heard of Einstein’s famous formula relating energy and mass,
where E is energy, m is mass, and c is the speed of light (186,000 mi/s). In this sec-
tion we study formulas and how they are used to model real-world phenomena.
E = mc
2
V
P = kT>VA = pr
2
2
■ What Is a Formula?
A formula is simply an equation involving variables. The term formula is employed
when an equation is used to calculate specific quantities (such as the area of a circle)
or when it is used to describe the relationship between real-world quantities (such as
the formula that relates pressure, volume, and temperature). Formulas provide a
compact way of describing relationships between real-world quantities. Many of the
equations we encountered in the preceding sections, such as the equation ,
which relates the distance d an object falls to the time t it has been falling, are also
called formulas. In this section we study formulas that involve several variables. We
learn to read formulas, that is, to understand what the form of a formula tells us. We
also learn to find and use formulas.
For example, suppose you’re paid $8 an hour at your part-time job. If we let n
stand for the number of hours you work and P stand for your pay, then your pay is
modeled by the formula . This formula works as long as the pay is $8 an hour.
We can find a formula that models your pay for any hourly wage w:
where , , and . (Notice how we use
letters that help us remember what the variables mean: P for pay, w for wage, n for
number of hours worked.) We can read this formula as
“Pay equals hourly wage times the number of hours worked”
The algebraic structure of this formula tells us how the variables are related. For
example, since w and n are multiplied together to give P, it follows that the larger w
or n is, the larger P is. In other words, if you get a larger hourly wage or you work
more hours, you’ll get paid more.
n = number of hours workedw = wageP = pay
P = wn
P = 8n
d = 16t
2

2
■ Finding Formulas
In the next two examples we explore the process of finding formulas that model real-
life situations. In trying to find a formula, it’s often helpful to try a simple example
with small numbers to see more easily how the variables in the model are related.
example
1
Finding a Formula for Gas Mileage
The “gas mileage” of a car is the number of miles it can travel on one gallon of gas.
(a) Find a formula that models gas mileage in terms of the number of miles driven
and the number of gallons of gasoline used.
(b) Mike’s car uses 10.5 gallons to drive 230 miles. Find its gas mileage.
102 CHAPTER 1
■
Data, Functions, and Models
In Words In Algebra
Number of miles driven N
Number of gallons used
G
Gas mileage (mi/gal) M
We can now express the formula we want as follows:
(b) To get the gas mileage, we use the formula we have just found. We substitute
230 for N and 10.5 for in the formula.
Formula
Replace N by 230 and by 10.5
Calculator
The gas mileage for Mike’s car is 21.9 mi/gal.
■ NOW TRY EXERCISE 21 ■
L 21.9
G =
230
10.5
M =
N
G
G
M =
N
G
Thinking About the Problem
Let’s try a simple case. If a car uses 2 gallons to travel 100 miles, then it would
travel just 50 miles on one gallon; that is, we can see that
/gal
So “gas mileage” is the number of miles driven divided by the number of gal-
lons used.
gas mileage =
100 miles
2 gallons
= 50 mi
Solution
(a) From the simple example above we can express the formula in words as
To express the model as a formula, we need to assign symbols to the variables
involved.
gas mileage =
number of miles driven
number of gallons used
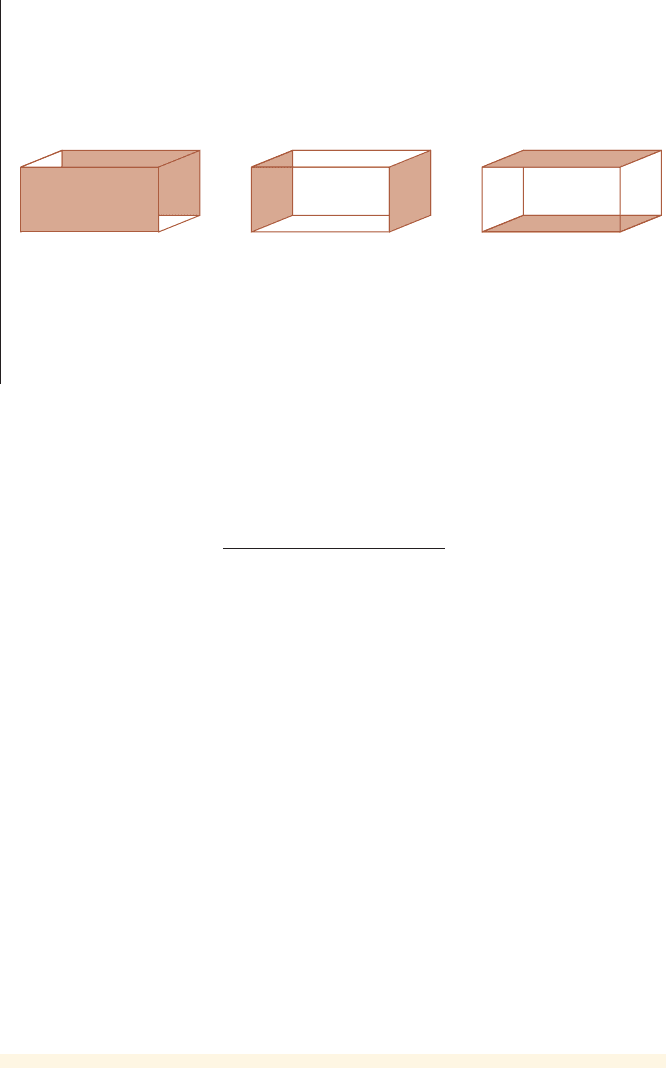
SECTION 1.9
■
Making and Using Formulas 103
example
2
Finding a Formula for Surface Area
A rectangular box is to be made of plywood.
(a) Find a formula for the area of plywood needed to build a box of any size.
(b) Find the area of plywood needed to build a box 8 ft long, 5 ft wide, and 3 ft
high.
Thinking About the Problem
We want a formula for the surface area of a box. A sketch of a box shows that
the front and back of the box have identical areas; the same holds for the left and
right sides and the top and bottom.
So we conclude that
Since the front, side, and bottom are rectangles, we can easily find their areas.
Solution
(a) To express the surface area as a formula, we need to assign symbols to the
variables involved.
surface area = 2 * 1area of front2+ 2 * 1area of side2+ 2 * 1area of bottom2
h
l
w
h
l
w
h
l
w
In Words In Algebra
Length l
Width w
Height h
Surface area S
We need to express the following “word” formula as an algebraic formula:
Now, the area of the front is lh, the area of a side is wh, and the area of the bot-
tom is lw. So we can now express the formula we want as
(b) To get the surface area of the box that we want to build, we use the formula
we found in part (a), replacing l by 8, w by 5, and h by 3:
Formula
Replace l by 8, w by 5, and h by 3
Calculator
The area of plywood needed to build this box is .
■ NOW TRY EXERCISE 17 ■
158 ft
2
= 158
= 218
#
32+ 215
#
32+ 218
#
52
S = 2lh + 2wh + 2lw
S = 2lh + 2wh + 2lw
surface area = 2 * 1area of front2+ 2 * 1area of side2+ 2 * 1area of bottom2
