Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

84 CHAPTER 1

■

Data, Functions, and Models

25. 26.

27–32

■ A function f is given.

(a) Use a graphing device to draw the graph of f.

(b) State approximately the intervals on which f is increasing and on which f is

decreasing.

27. 28.

29. 30.

31. 32.

33–36

■ The graph of a function is given.

(a) Find all the local maximum and minimum values of the function and the value of x

at which each occurs.

(b) Find the intervals on which the function is increasing and on which the function is

decreasing.

33. 34.

35. 36.

37–40

■ A function is given. Use a graphing calculator to draw a graph of the function.

(a) Find all the local maximum and minimum values of the function and the value of x

at which each occurs. State each answer correct to two decimals.

(b) Find the intervals on which the function is increasing and on which the function is

decreasing. State each answer correct to two decimal places.

37. 38.

39. 40. G 1x 2= x 2x - x

F 1x 2= x 16 - x

g1x 2= 3 + x + x

- x

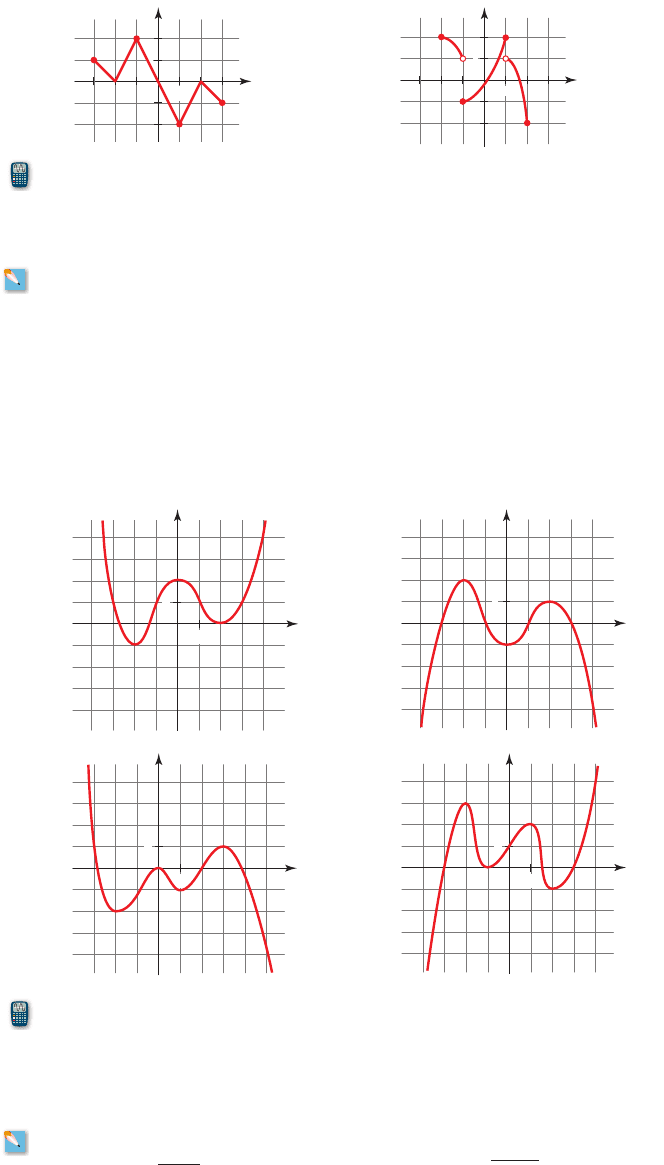
f 1x 2= x

- x

f 1x 2= x

- 4x

+ 2x

+ 4x - 3f 1x 2= x

+ 2x

- x - 2

f 1x 2= x

- 16x

f 1x 2= 2x

- 3x

- 12x

f 1x 2= x

- 4xf 1x 2= x

- 5x

SECTION 1.7

■

Working with Functions: Getting Information from the Graph 85

CONTEXTS

P (MW)

Source: Pacific Gas & Electric.

181512963

t (h)

400

600

800

200

41. Power Consumption The figure shows the power consumption in San Francisco for

September 19, 1996. (P is measured in megawatts; t is measured in hours starting at

midnight.)

(a) What was the power consumption at 6:00

A.M.? At 6:00 P.M.?

(b) When was the power consumption a maximum?

(d) What is the net change in the values of P as the value of x changes from 0 to 12?

Source: California Department of Mines and Geology.

a (cm/s

)

−50

10 15 20 25

t (s)

100

42. Earthquake The graph shows the vertical acceleration of the ground from the 1994

Northridge earthquake in Los Angeles, as measured by a seismograph. (Here t

represents the time in seconds.)

(a) At what time t did the earthquake first make noticeable movements of the earth?

(b) At what time t did the earthquake seem to end?

(d) What is the approximate net change in the intensity of the earthquake as the value

of t changes from 5 to 30?

43. Low Temperatures In January 2007 the state of California experienced remarkably

cold weather. Many crops that usually thrive in California were lost because of the frost.

Orange crops just ripening in Tulare County, California, were frozen on the trees. The

table and graph on the next page show the daily low temperatures T in Tulare County

for the month of January 2007.

(a) Find and .

(b) Which is larger, ?

lowest?

(d) Find the net change in the daily low temperatures from January 1 to January 31.

T 115 2 or T 119 2

T 115 2T 112

44. Population of Philadelphia The table and graph below show the history of the

population P of the city of Philadelphia from 1790 to 2000.

(a) Find and .

(b) Which is larger, or ?

Philadelphia have a population over 1.8 million?

(d) Find the net change in the population of Philadelphia from 1950 to 2000.

P 1210 2P 11602

P12002P 11002

45. Weight Function The graph gives the weight W of a person at age x.

(a) Determine the intervals on which the function W is increasing and on which it is

decreasing.

(b) What do you think happened when this person was 30 years old?

Years

since 1790

Population

(ⴛ 10,000)

0 2.85

10 4.12

20 5.37

30 6.38

40 8.05

50 9.37

60 12.14

70 56.55

80 67.40

90 84.72

100 104.70

Years

since 1790

Population

(ⴛ 10,000)

110 129.37

120 154.90

130 182.34

140 195.10

150 193.13

160 207.16

170 200.25

180 194.86

190 168.82

200 158.56

210 151.76

150

200

100

50 100 150 200

Years since 1790

Population

(⫻ 10,000)

100

Weight

(lb)

150

200

10 20 30 40 50 60 70

Age (yr)

86 CHAPTER 1

■

Data, Functions, and Models

10 20 30

Day

Daily low

temperature

(°F)

1 32

2 30

3 32

4 35

5 33

6 28

7 28

8 28

9 28

10 30

11 33

Day

Daily low

temperature

(°F)

12 24

13 23

14 21

15 20

16 23

17 26

18 26

19 24

20 26

21 28

22 26

Day

Daily low

temperature

(°F)

23 28

24 28

25 30

26 32

27 33

28 46

29 37

30 39

31 39

SECTION 1.7

■

Working with Functions: Getting Information from the Graph 87

46. Distance Function The graph gives a sales representative’s distance from his home

as a function of time on a certain day.

(a) Determine the time intervals on which his distance from home was increasing and

on which it was decreasing.

(b) Describe in words what the graph indicates about his travels on this day.

Distance

from home

(mi)

8:00

A.M. 6:00 P.M.10:00 NOON 2:00 4:00

Time

(

)

47. Running Race Two runners compete in a 100-meter race. The graph in the margin

depicts the distance run as a function of time for each runner.

(a) Did each runner finish the race? Who won the race?

(b) At what time did one runner overtake the other?

48. Education and Income The graph shows the yearly median income H for Americans

with a high school diploma, the yearly median income B of Americans with a bachelor’s

degree, and the yearly median income M of Americans with a master’s degree, all in the

time period 1991 to 2003 (with corresponding to 1991).

(a) Find the interval on which all three functions are decreasing.

(b) Find the net change of each function from 1995 to 1999. Which function had the

most net change in this time period?

x = 0

100

t (s)

y (m)

Distance

Time

123456789101112

Year

Income

(⫻ $1000)

49. Migrating Fish Suppose a fish swims at a speed relative to the water, against a

current of 5 mi/h. Using a mathematical model of energy expenditure, it can be shown

that the total energy E required to swim a distance of 10 mi is given by

Biologists believe that migrating fish try to minimize the total energy required to swim

a fixed distance.

(a) Graph the function E in the viewing rectangle [5.1, 10] by [4000, 13,000].

(b) Where is the function E increasing and where is the function E decreasing?

E 1√2= 2.73√

√ - 5

5.1 … √ … 10

√

0.2

0.1

Alcohol

consumption

(mg/mL)

0.5 1.0 1.5 2.0 2.5 3.0

Time (h)

88 CHAPTER 1

■

Data, Functions, and Models

[Note: This result has been verified; migrating fish swim against a current at a speed

50% greater than the speed of the current.]

50. Coughing When a foreign object that is lodged in the trachea (windpipe) forces a

person to cough, the diaphragm thrusts upward, causing an increase in pressure in the

lungs. At the same time, the trachea contracts, causing the expelled air to move faster

and increasing the pressure on the foreign object. According to a mathematical model of

coughing, the velocity of the air stream through an average-sized person’s trachea is

related to the radius r of the trachea (in centimeters) by the function

(a) Graph the function .

(b) Where is the function increasing and where is the function decreasing?

maximum occur?

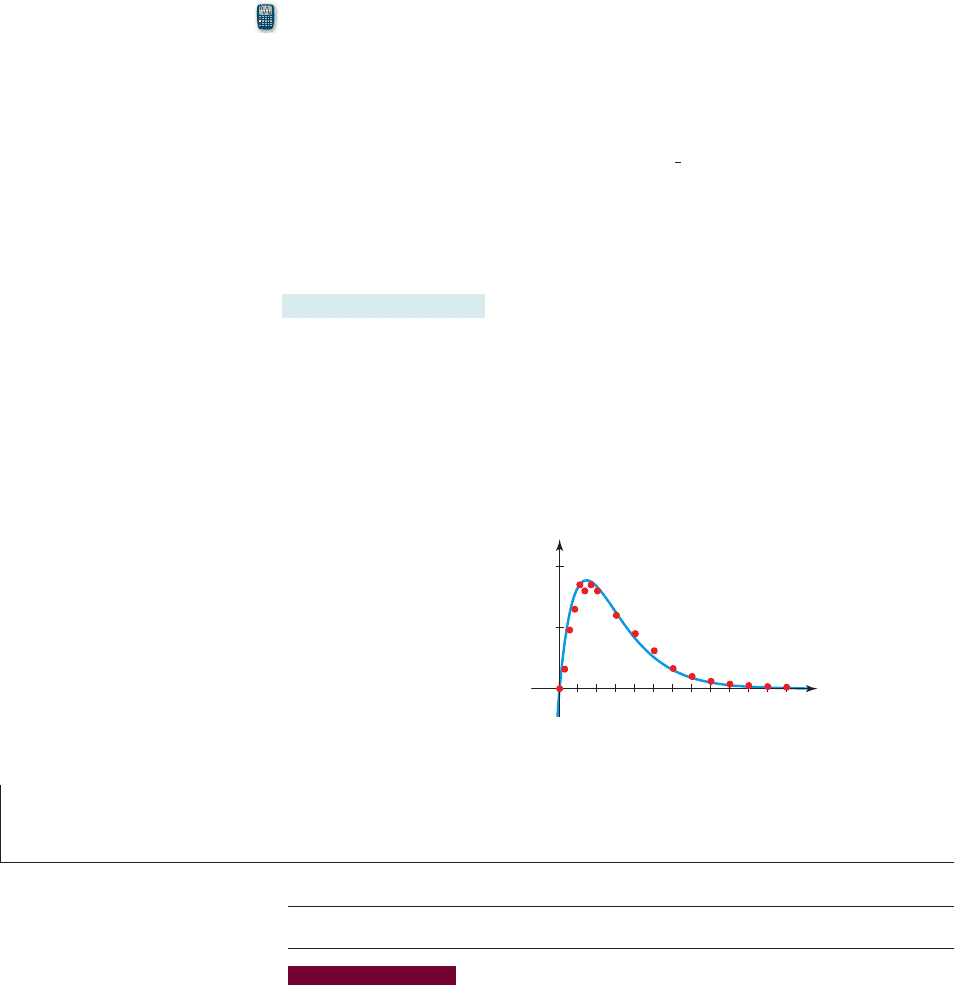
51. Algebra and Alcohol The first two columns of the table in the Prologue (page P2)

give the alcohol concentration at different times in a three-hour interval following the

consumption of 15 mL of alcohol. The data are modeled by the function A, which is

graphed below together with a scatter plot of the data. (In Chapter 5 we learn how to

find an algebraic expression for the function A.)

(a) Use the graph of A to determine at what time the alcohol concentration is at its

maximum level.

(b) On what time interval is the alcohol concentration increasing?

√

√√

√

√ 1r 2= 3.211 - r2r



… r … 1

√

1.8 Working with Functions:

Modeling Real-World Relationships

■

Modeling with Functions

■

Getting Information from the Graph of a Model

IN THIS SECTION... we make real-world models, not from data but from a verbal

description. This includes models for cost, revenue, or depletion of resources and models

that depend on some geometrical property. Once a model has been found, we use it to get

information about the thing being modeled.

In Section 1.3 we learned how to find equations that model real-world data. In

Sections 1.5–1.7 we used functions to model the dependence of one changing quan-

tity on another. In this section we explore the process of making a model from a ver-

bal description of a real-world situation.

SECTION 1.8

■

Working with Functions: Modeling Real-World Relationships 89

Recall that a model is a mathematical representation (such as an equation or a

function) of a real-world situation. Modeling is the process of making mathematical

models. Why make a mathematical model? Because we can use the model to answer

questions and make predictions about the thing being modeled. The process is de-

scribed in the following diagram.

■ Modeling with Functions

We observed in Section 1.3 that many real-world situations can be described by lin-

ear models. It is useful to express a linear model in function form; this helps us to

obtain information more easily from the model. We begin by creating a linear model

for a situation that is described verbally.

example

A Model for Cost

A company manufactures baseball caps with school logos. The company charges their

customers a fixed fee of $500 for setting up the machines and $8 for each cap produced.

(a) Find a linear model for the cost of purchasing any number of caps from this

company. Express the model in function form.

(b) Use the model to find the cost of purchasing 225 caps.

Solution

(a) To find a linear model, we need to assign letters to the quantities involved. Let

n represent the number of caps to be purchased. The model we want is a

function C that gives the cost of purchasing n caps. From the information

given, we can write

We put this model in function form:

(b) To find the cost of purchasing 225 caps, we need to find C(225):

Model

Replace n by 225

Calculator

The cost is $2300.

■ NOW TRY EXERCISE 17 ■

= 2300

C12252= 500 + 812252

C1n2= 500 + 8n

C 1n2= 500 + 8n

C = 500  + 8n

ModelReal world

Making a model

Usin

the model

Fixed cost Add $8 for each cap

IN CONTEXT ➤

90 CHAPTER 1

■

Data, Functions, and Models

The state of the environment has played an important role in the rise and fall of

civilizations throughout history. For example, deforestation is thought to have played

a significant role in the decline of the once-flourishing Easter Island culture in the

South Pacific. The decline of the world’s rain forests is a controversial topic fre-

quently discussed in the news. Fortunately, wise forest management practices are

now common in many parts of the world, promising a healthier environment for gen-

erations to come. The next example illustrates the impact that paper usage has on our

forests.

example

A Function Model for Paper Consumption

The average U.S. resident uses 650 lb of paper a year. The average pine tree produces

4130 lb of paper.

(a) Find a function N that models the number of trees used for paper in one year

by x U.S. residents.

(b) The city of Cleveland Heights, Ohio, had a population of about 49,000 in

2003. Use the model to find the number of trees required to make the paper

used by the residents of Cleveland Heights in 2003.

Solution

(a) Since each resident uses an average of 650 lb of paper a year and each tree

produces 4130 lb of paper, the number of trees each person uses per year is

So each resident uses about 0.157 tree per year. Thus, x residents use 0.157x tree

per year.

The model we want is a function N that gives the number of trees used by

x residents. We can now describe this function as follows:

Model

N1x 2= 0.157x

L 0.157 tree

650 lb

4130 lb

trees used by each resident =

amount of paper used by each resident 1lb 2

amount of paper each tree produces 1lb

Deforested Easter IslandLong-leaf pine forest

James Thew/Shutterstock.com 2009

Vladimir Korostyshevskiy/Shutterstock.com

/tree)

SECTION 1.8

■

Working with Functions: Modeling Real-World Relationships 91

(b) For Cleveland Heights the number of residents x is 49,000. Using the model,

we have

Model

Replace x by 49,000

Calculator

So the Cleveland Heights residents used about 7693 trees in 2003.

■ NOW TRY EXERCISE 19 ■

= 7693

N149,0002= 0.157149,0002

N1x2= 0.157x

example

Irrigating a Garden

A gardener waters his vegetable plot using a drip irrigation system. Water flows

slowly from a 1200-gallon tank through a perforated hose network to keep the soil

appropriately moist. During the spring planting season, the garden requires 80 gal-

lons of water per day.

(a) Find a function W that gives the amount of water in the tank x days after it has

been filled.

(b) Use the function W to find the water remaining in the tank after 3 days and

after 12 days.

(d) How many days will it take for the tank to empty?

(e) The gardener prefers not to let the tank empty completely. Instead, he decides

to refill it when the level has dropped to 200 gallons. How many days will it

take for the water level to drop to this level?

Thinking About the Problem

Let’s try a simple case. If the garden has been watered for 10 days after the

tank has been filled, how much water is left in the tank? Since the garden re-

quires 80 gal of water per day, the number of gallons used in 10 days is

So the number of gallons left in the tank is

So the amount left in the tank is the number of gallons in a full tank minus the

amount of water used per day times the number of days since the tank was

filled.

Solution

(a) We need to find the rule W that takes the input x (the number of days since the

tank was filled) and gives as output the number of gallons of water W(x)

remaining in the tank. We know that the gardener starts out with 1200 gallons

and uses 80 gallons per day, so we must subtract the total water usage after

x days from the initial amount in the tank to find the number of gallons left in

the tank. Let’s express these quantities in symbols.

day2110 days2= 1200 - 800 = 400 gal1200 gal - 180 gal

day2110 days2= 800 gal180 gal

In Words In Algebra

Days since fill-up x

Gallons used each day 80

Gallons used since fill-up 80x

Gallons left in tank

1200 - 80x

So the function W that models the amount of water left in the tank is

Model

(b) To find the water level in the tank after 3 days and after 12 days, we evaluate

the function W at 3 and at 12:

Replace x by 3

Replace x by 12

So the water level after 3 days is 960 gal, and after 12 days is 240 gal.

Replace x by 20

We get a negative value for W(20). It is impossible for the tank to contain a neg-

ative amount of water, so this must mean that the gardener would run out of wa-

ter before 20 days have passed.

(d) An empty tank means that the water level has dropped to zero; that is,

Model

Replace W(x) by 0 and switch sides

Add 80x to each side

Divide by 80 and switch sides

Calculator

The tank will empty after 15 days.

(e) We need to find how many days x it takes for the water level W(x) to drop to

200.

Model

Replace W(x) by 200 and switch sides

Subtract 200 from each side

Add 80x to each side

Divide by 80, switch sides

Calculator

The gardener needs to refill the tank every days.

■ NOW TRY EXERCISE 21 ■

x = 12.5

x =

1000

1000 = 80x

1000 - 80x = 0

1200 - 80x = 200

W1x2= 1200 - 80x

x = 15

x =

1200

1200 = 80x

1200 - 80x = 0

W1x2= 1200 - 80x

W1x 2= 0

W1202= 1200 - 801202=-400

W1122= 1200 - 801122= 240

W132= 1200 - 80132= 960

W1x 2= 1200 - 80x

92 CHAPTER 1

■

Data, Functions, and Models

Solving equations is reviewed in

Algebra Toolkit C.1, page T47.

SECTION 1.8

■

Working with Functions: Modeling Real-World Relationships 93

■ Getting Information from the Graph of a Model

We now model real-world phenomena by a function, then use the graph of the func-

tion to get information about the thing being modeled.

example

Modeling the Volume of a Box

A breakfast cereal company manufactures boxes to package their product. For aes-

thetic reasons, the box must have the following proportions: Its width is 3 times its

depth, and its height is 5 times its depth.

(a) Find a function that models the volume of the box in terms of its depth, and

graph the function.

(b) Find the volume of the box if the depth is 1.5 in.

(d) For what depth is the volume greater than 60 ?

Thinking About the Problem

Let’s experiment with the problem. If the depth is 1 in., then the width is 3 in.

and the height is 5 in. So in this case the volume is .

The table gives other values. Notice that all the boxes have the same shape, and

the greater the depth, the greater the volume.

V = 1 * 3 * 5 = 15 in

Depth Volume

1 * 3 * 5 = 15

2 * 6 * 10 = 120

3 * 9 * 15 = 405

4 * 12 * 20 = 960

Solution

(a) To find the function that models the volume of the box, we first recall the

formula for the volume of a rectangular box.

There are three varying quantities: depth, width, and height. Because the func-

tion we want depends on the depth, we let

Then we express the other dimensions of the box in terms of x.

x = depth of the box

volume = depth * width * height

In Words In Algebra

Depth x

Width 3x

Height 5x