Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

304 CHAPTER 3

■

Exponential Functions and Models

In a growth (or decay) model, the growth (or decay) rate is the proportion by

which the quantity being modeled grows (or decays) in each time period, expressed

as a fraction, decimal, or percentage. The growth (or decay) rate r is related to the

growth (or decay) factor a by the formula

For a growth model we have , and for a decay model we have , because

in a growth model, the amount is increasing, whereas in a decay model, the

amount is decreasing.

3.2 Exponential Models: Comparing Rates

We may wish to change the length of the time period that we use to measure the time

x in a growth or decay model. (For instance, we may prefer to measure time in days in-

stead of weeks.) Let t represent the number of new time intervals that correspond to

x old time intervals. If x and t are related by , then the exponential model

can be rewritten as the model

where .

An example of exponential growth is the growth of money invested in an ac-

count that pays compound interest. This is modeled by the exponential function

■

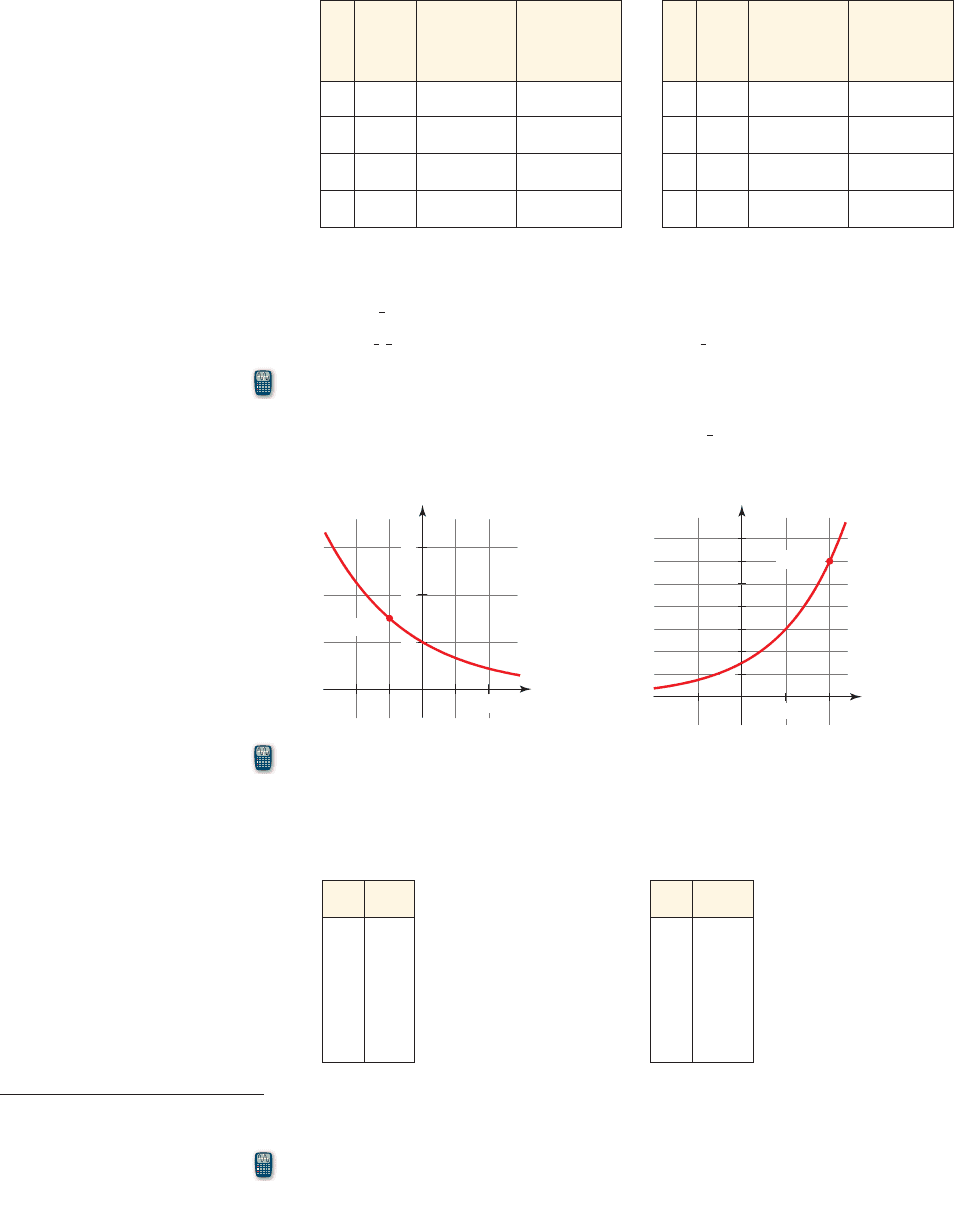
is the amount in the account after t years.

■

P is the original principal that was invested.

■

r is the annual interest rate (expressed as a decimal), compounded n times a

year.

The rate of radioactive decay is usually expressed in terms of the half-life, the

time required for a sample to decay to half of its initial mass. The decay model can

be expressed as

where is the mass remaining of an initial mass C after time t, expressed in the

same units as the half-life h.

m 1t2

m 1t2= CA

t>h

A 1t2

A 1t2= P a1 +

b = a

f 1t2= Ca

= Cb

f 1x2= Ca

x = kt

f 1x2

r 6 0r 7 0

a = 1 + r

Exponential growth, a>1

f(x) = Ca˛

Exponential decay, 0<a<1

CHAPTER 3

■

Review 305

3.3 Comparing Linear and Exponential Growth

Whereas linear models have constant average rate of change, exponential growth or

decay models have constant percentage rate of change. The percentage rate of

change of an exponential function is the average rate of change between any two in-

puts that are one unit apart (x and ), expressed as a percentage of the value

at x. This difference is the main feature that sets the two types of models apart.

When population growth experiences limited resources, a logistic growth

model is often appropriate. A logistic model is a function of the form

Here, x is the number of time periods, and C is the carrying capacity, the maximum

population the resources can support.

3.4 Graphs of Exponential Functions

An exponential function with base a is a function of the form

Exponential functions have the following properties:

■

The domain is all real numbers, and the range is all positive real numbers.

■

The line y = 0 (the x-axis) is a horizontal asymptote of f.

■

The graph of f has one of the following shapes:

If , then f is an increasing function.

If , then f is a decreasing function.a 6 1

a 7 1

f 1x2= a

a 7 0, a ⫽ 1

f 1x2=

1 + b

-x

a 7 1

x + 1

3.5 Fitting Exponential Curves to Data

Suppose that the scatter plot of a data set indicates that the data seem to be best mod-

eled by an exponential function. Then we can use the ExpReg feature on a graphing

calculator to find the exponential curve

that best fits the data.

y = a

Ï=a˛ for a>1 Ï=a˛ for 0<a<1

(0,

(0, 1)

y y

306 CHAPTER 3

■

Exponential Functions and Models

REVIEW EXERCISES

1–4 ■ The given function is a model for exponential growth or decay.

(a) Is it a growth model or a decay model?

(b) What is the growth or decay factor?

(d) What is the initial amount?

1. 2.

3. 4.

5–8

■ A bacteria population P initially has the given size C, and in each 3-hour time period

it experiences the growth (or decay) described.

(a) Find an exponential model for the population as a function of x, the number of

3-hour time periods that have passed.

(b) Find a model for the population as a function of t, the number of hours that have

passed.

answer from each model?

5. 6.

7. 8.

9–10

■ An investment of $24,000 is invested in a CD paying the given annual interest rate,

compounded as indicated. Find the amount in the account after each given time

period.

9. 3.6% interest, compounded monthly

(a) 1 year (b) 3 years (c) 4 years and 6 months

10. 1.2% interest, compounded daily

(a) 2 years (b) 10 years (c) 50 years

11–12

■ A radioactive element, its initial mass, and its half-life h (in years) are given.

(a) Find a function of the form that models the mass of the element

remaining after t years.

(b) Find the mass remaining after 25 years.

(d) What is the annual decay rate?

11. Radium-226, 300 kg, 1600 years 12. Strontium-90, 35 g, 28 years

13–14

■ Complete the table by calculating the average rate of change and the percentage

rate of change for f. Then find an exponential model for the given data.

m 1t 2= Ca

m 1t 2= CA

t>h

C = 70,P increases by 25%C = 1320,P decreases by 30%

C = 14,000,

P is cut in halfC = 200,P doubles

k 1x 2= A

h 1x 2= 8A

g1x 2= 125010.97 2

f 1x 2= 100011.252

CHAPTER

SKILLS

To determine whether an exponential model is appropriate, we can check to see

whether the percentage rate of change between equally spaced inputs is approxi-

mately the same. If so, then an exponential model is appropriate.

When modeling population growth that is limited by the availability of essential

resources, we can use the Logistic feature on a graphing calculator to find the lo-

gistic growth model of the following form to best fit the data (where a, b, and C are

positive constants):

N =

1 + b

-x

CHAPTER 3

■

Review Exercises 307

f 1t 2

Average

rate of

change

Percentage

rate of

change

0 5000 — —

1 6000

2 7200

3 8640

13. 14.

15–18 ■ Sketch a graph of the exponential function by first making a table of values. Is the

function increasing or decreasing?

15. 16.

17. 18.

19–20

■ Use a graphing calculator to draw graphs of both f and g on the same screen. Find

the intersection point of the graphs.

19. 20. and

21–22

■ Find the exponential function whose graph is given.

21. 22.

f 1x 2= Ca

g1x 2= 211.5 2

f 1x 2= A

f 1x 2= 3

and g1x 2= 2

-x

k 1t 2=

-t

h 1t 2=

g1x 2= 10.62

f 1x 2= A

f 1t 2

Average

rate of

change

Percentage

rate of

change

0 270 — —

1 180

2 120

3 80

f 1t 2

0 400

2 424

4 462

6 491

8 519

10 553

2_2

(_1, 1.5)

(2, 12)

23–24 ■ A data set is given in the table.

(a) Make a scatter plot of the data.

(b) Use a calculator to find an exponential model for the data.

model appear to fit the data well?

23. 24.

f 1t 2

0 1225

5 1092

10 985

15 880

20 792

25 718

These exercises test your understanding by combining ideas from several sections in a

single problem.

25. Linear, Exponential, or Logistic? Three coastal communities were established in the

year 2000. The tables show the growth in the number of housing units in each

community in the period from 2000 to 2006 (with year 0 representing 2000).

CONNECTING

THE CONCEPTS

308 CHAPTER 3

■

Exponential Functions and Models

Avalon Acres Buccaneer Beach Coral Cay

Year Dwellings

0 250

1 296

2 359

3 434

4 520

5 620

6 751

Yea r Dwellings

0 200

1 218

2 241

3 255

4 284

5 296

6 322

Year Dwellings

0 190

1 210

2 245

3 281

4 302

5 308

6 312

(a) Make scatter plots for each of the data sets.

(b) On the basis of your scatter plots, what kind of model best represents the growth of

housing units in each town: linear, exponential, or logistic?

community.

(d) Use your models from part (c) to determine: (i) The growth rate in the town with

the linear model. (ii) The percentage growth rate in the town with the exponential

model. (iii) The carrying capacity in the town with the logistic model.

(e) What planning policies or other factors might account for the differences in the

type of growth that each community experiences?

26. Bacterial Infection A horse is infected with a bacterium that may cause death if the

bacteria count becomes sufficiently large. The table gives the number of bacteria in the

horse at 20-minute intervals since infection.

(a) Find the growth factor (per 20-minute time period) for the bacteria population.

(b) Find a model of the form for the bacteria population after x time periods.

infection.

(d) Graph your model from part (c) on a graphing calculator. Use the feature

to determine how many hours it will take for the bacteria count to reach 500

million, the lethal level.

(e) Use a graphing calculator (TI-89 or better) to find a logistic model for the data.

Graph the model on a scatter plot of the data. Does it seem to fit the data well?

(f) If the logistic model is in fact the correct one, will the bacteria count ever reach the

lethal level of 500 million, or will the horse survive?

TRACE

P 1x 2= Ca

27. Aspirin Metabolism When a standard dose of 650 mg of aspirin is ingested, it is

metabolized at an exponential rate. For the average person the half-life of the aspirin

remaining in the body is 50 minutes.

(a) Find an exponential function of the form that models the amount of

aspirin remaining in the body after x 50-minute time periods.

(b) Change the time interval to find a function that models the amount of

aspirin in the body after t hours.

(d) Use a table of values to plot a graph of the amount of aspirin in the body over the

first 10-hour period after ingesting it.

. Fruit Fly Population A messy student leaves discarded food scattered around his

dorm room, attracting fruit flies. From an initial population of 10 flies, the population

grows exponentially, tripling every four hours.

(a) Find an exponential function of the form that models the number of

fruit flies in the room after x four-hour time periods.

P 1x 2= Ca

A 1t 2= Cb

A 1x 2= Ca

CONTEXTS

Time

(min)

Bacteria

(millions)

0 0.5

20 1.5

40 4.5

60 13.5

80 40.5

CHAPTER 3

■

Review Exercises 309

Year 0 1 2 3 4 5 6

Turtles 15 23 34 41 48 50 51

Month 0 1 2 3 4 5 6

Bond A

$5000 $5025 $5050

Bond B

$5000 $5025 $5050.13

(b) For which bond is the growth of the investment value linear? What is the monthly

growth rate?

growth factor? What is the monthly percentage growth rate?

(d) What is the value of each of the investments when the bonds mature after one year?

(e) Which bond would you choose to buy yourself? Why?

31. Turtle Population Fifteen pet turtles escape from their owner’s home on a private

Caribbean island. Over the years their population increases, as indicated in the table

(where “year” indicates years since escape).

(a) Make a scatter plot of the data. Which would seem to be a better model for the

population: an exponential model or a logistic model?

(b) Change the time interval to find a function that models the number of

fruit flies in the room after t hours.

growth rate?

(d) The student goes home for Thanksgiving without cleaning his room, allowing the

flies to flourish. How many flies will there be in the room when he returns, 2 days

after they made their initial appearance?

. Investments Marie-Claire has received an unexpected bonus of $7500 from her

employer and is trying to decide which of two 3-year CD offers from her bank would be

a better way to invest the money:

■

Plan A offers a 4% annual interest rate, compounded monthly.

■

Plan B offers a 3% annual interest rate, compounded quarterly, but then adds an

extra 2% of the principal at the end if the CD is held to maturity.

Calculate the amount to which her money would grow under each plan at the end of the

3 years. Which plan is better?

30. Bond Interest Some savings bonds pay a fixed rate of interest, which is issued to the

owner at the end of every month. (These are known as coupon bonds.) Others are like

CDs, for which the interest is compounded and paid out with the principal when the

bond matures. Joshua purchases a one-year $5000 bond of each type, each paying 6%

annual interest.

■

Bond A provides Joshua a check for his interest on just the principal every month.

He gets his principal back with his last interest payment at the end of the year.

■

Bond B credits Joshua’s bond with the interest, compounding it monthly, and

then gives him his principal plus accumulated interest at the end of the year.

(a) Complete the following table giving the value of Joshua’s investment (principal

plus interest) at the end of each of the first six months that he owns the bonds.

P 1t 2= Cb

310 CHAPTER 3

■

Exponential Functions and Models

(b) Use a graphing calculator to find both an exponential and a logistic model for the

data. Graph both functions on your scatter plot, and decide which one you feel fits

the data better.

after 100 years. Which model seems more reasonable?

32. Diminishing Returns An athlete wishes to improve her performance in the

100-meter sprint. The data in the table below give her time (in seconds) for this sprint

on each Monday of an intensive six-week training program.

(a) Use a graphing calculator (TI-89 or better) to find a logistic model for her sprint

time.

(b) Graph both the data and the model on the same viewing rectangle. What does her

best possible time appear to be, on the basis of the carrying capacity of the model?

(to two decimal places)?

Week number 0 1 2 3 4 5 6

Sprint time (s) 14.9 14.0 13.4 13.0 12.7 12.6 12.5

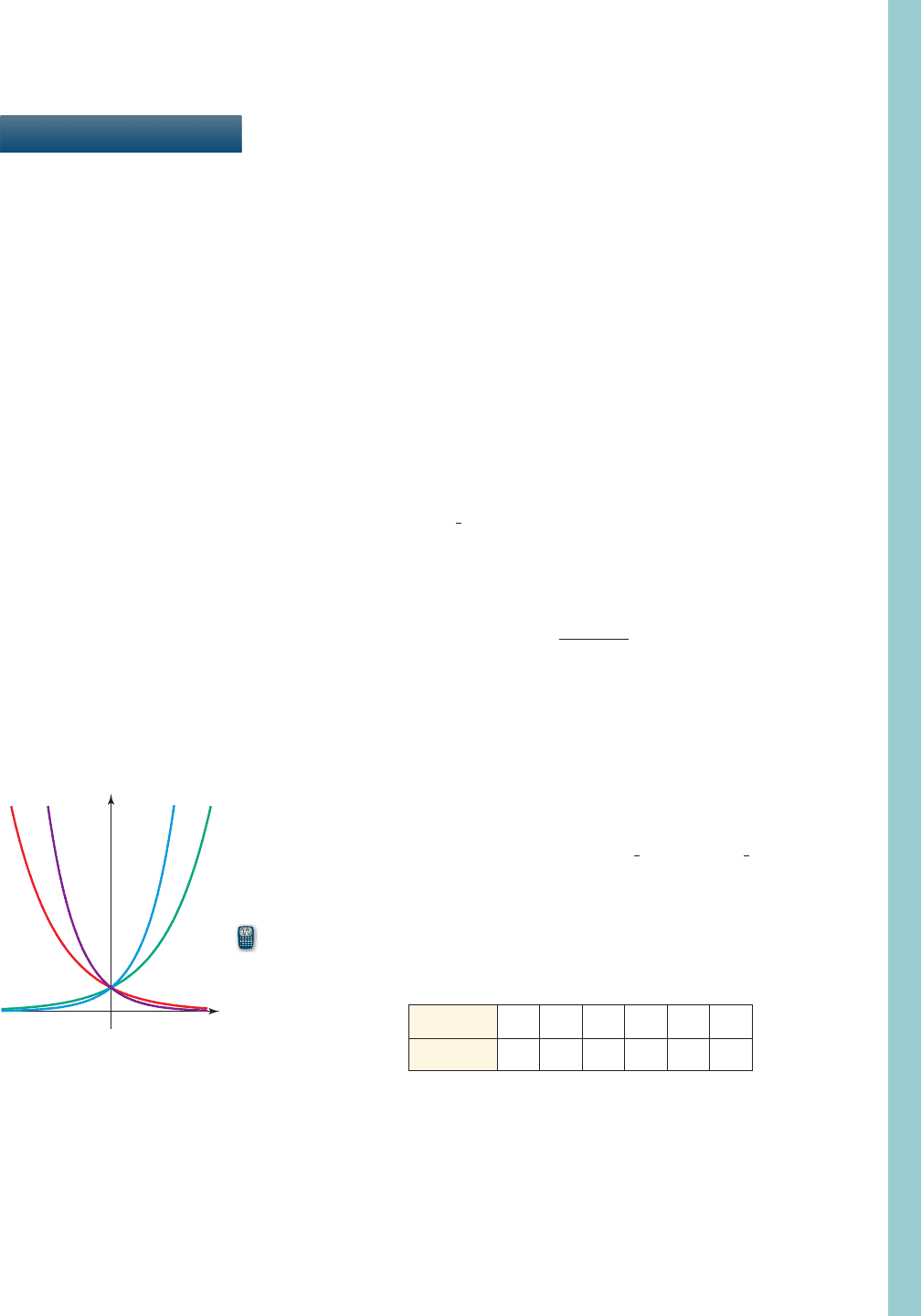
CHAPTER 3

■

Test 311

TEST

1. The growth of a population is modeled by the exponential function

where x represents time measured in days.

(a) What is the initial population?

(b) What is the growth factor? What is the growth rate?

(d) Make a table of values for x = 0, 1, 2, 3, and use it to sketch a graph of P.

(e) What is the one-week growth factor for the population? Find a model of the form

for the population, where t is measured in weeks.

2. Marla opens a savings account that is guaranteed to pay an annual interest rate of 3.6%,

compounded monthly. She deposits $2000 into the account.

(a) Find the amount in Marla’s account after 4 months, after 1 year, and after 3 years.

(b) Marla had the option of an account that pays 3.45% annual interest, compounded

daily. Would she have seen better returns with that account?

3. For the function , find the average rate of change and the percentage rate of

change between the indicated values of x.

(a) Between 0 and 2 (b) Between 2 and 4

4. A population is modeled by the function

where t is time measured in years.

(a) What is this type of growth model called?

(b) What is the initial population?

(d) Will the population ever reach 600? Why or why not? [Hint: Think about the

carrying capacity.]

5. The figure in the margin shows the graphs of the four exponential functions

For each graph determine which function it is the graph of. Explain the reasons for your

choices.

6. Some species of fungi form colonies of cells that grow without bound (assuming that

sufficient resources are present). A scientist records the mass of such a colony every

week; his results are given in the table below.

f 1x2= 2

,g1x 2= 3

,h1x 2= A

,k1x 2= A

P 1t2=

500

1 + 3

-t

F 1x 2=

P 1t 2= Cb

P 1x2= 640˛ 11.5 2

CHAPTER

Week 012345

Mass (kg) 1.2 1.7 2.8 3.9 6.1 9.0

(a) Use a graphing calculator to find (i) the linear model and (ii) the exponential model

that best fits the data.

(b) Make a scatter plot of the data, and graph both the models that you found in part (a)

on the scatter plot. Which model fits the data better?

Extreme Numbers: Scientific Notation

OBJECTIVE To use scientific notation to express enormously huge and incredibly

tiny numbers.

Have you ever wondered how many grains of sand there are on the world’s beaches? In

his book The Sand Reckoner Archimedes (ca. 200 B.C.) tries to estimate the number of

grains of sand it would take to fill the then known universe. Archimedes didn’t know

about our decimal system or our notation for exponents; that’s why it takes a whole book

to explain his estimate. Using exponents, however, it takes just a few symbols to express

gigantic numbers. For example, the number of grains of sand on the world’s beaches is

estimated at about grains (see www.hawaii.edu/swemath/jsand.htm).

Scientists routinely encounter extremely large numbers and extremely small

numbers. Here are some examples:

World population: 6.5 billion = 6,500,000,000

Mass of a hydrogen atom: 0.00000000000000000000000166 g

The world’s ant population is estimated at one quadrillion, and the insect population

is estimated at one quintillion. There are about 6 sextillion cups of water in the

world’s oceans, and each cup of water contains about 24 septillion atoms.

Inventing new names for ever larger numbers is an endless task, and the many

zeros needed to write extreme numbers in decimal notation can be difficult to read.

So scientists express such numbers as multiples of powers of 10.

312 CHAPTER 3

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

To write a number in scientific notation, express it in the form

where 1 and n is an integer.… a 6 10

a * 10

Using scientific notation, we express the world population as . The

positive exponent 9 indicates that the decimal point should be moved nine places to

the right:

Similarly, we can express the mass of a hydrogen atom as g. The neg-

ative exponent ⫺24 indicates that the decimal point should be moved 24 places to

the left:

I. Writing Numbers in Scientific Notation

First, let’s get some practice using scientific notation.

1. A number is given in decimal notation. Write the number in scientific notation.

Move decimal point 24 places to the left

1.66 * 10

-24

= 0.

000000000000000000000001 66

1.66 * 10

-24

6.5 * 10

= 6,500,000,000

6.5 * 10

Move decimal point

9 places to the right

Magdalena Bujak/Shutterstock.com 2009

Distance to the star nearest to our sun (Proxima Centauri):

40,000,000,000,000 km or _____________

Mass of the earth:

5,970,000,000,000,000,000,000,000 kg or _____________

Population of India in 2006:

1,100,000,000 or _____________

Diameter of a red blood cell:

0.0000007 m or _____________

Mass of an electron:

0.00000000000000000000000000091 g or _____________

2. A number is given in scientific notation. Write the number in decimal notation.

U.S. federal budget for 2007:

or ________________________

Weight of a hummingbird:

tons or ________________________

Population of China in 2006:

or ________________________

Number of cells in the average human body:

or ________________________

Radius of a gold atom:

m or ________________________

II. Calculating with Scientific Notation

We often need to multiply or divide numbers expressed in scientific notation. For ex-

ample, to find the time it takes light to reach us from the sun, we need to divide the

distance to the sun, mi, by the speed of light, mi/s. Scientific

notation allows us to multiply or divide large numbers easily.

1. Let’s see how to multiply two numbers given in scientific notation.

(a) Multiply the following two numbers. To keep your answer in scientific

notation, combine the powers of 10 separately.

(b) Multiply the following two numbers and write your answer in scientific

notation. Notice that the number is in scientific notation only if

= ________ * 10

ⵧ

= ________ * 10

ⵧ

18.4 * 10

2* 19.5 * 10

-3

2= 18.4 * 9.52110

* 10

-3

… a 6 10

a * 10

11.6 * 10

2* 12.5 * 10

2= 11.6 * 2.52110

* 10

2= ________ * 10

ⵧ

1.86 * 10

9.3 * 10

1.4 * 10

-10

4.9 * 10

1.3 * 10

3.5 * 10

-6

$2.8 * 10

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

EXPLORATIONS 313

4.0 * 10

$2,800,000,000,000