Stewart J. College Algebra: Concepts and Contexts
Подождите немного. Документ загружается.


324 CHAPTER 4
■
Logarithmic Functions and Exponential Models
2
4.1 Logarithmic Functions
■
Logarithms Base 10
■
Logarithms Base a
■
Basic Properties of Logarithms
■
Logarithmic Functions and Their Graphs
IN THIS SECTION… we define logarithms and study their basic properties.
GET READY… by reviewing the rules of exponents in Algebra Toolkits A.3 and A.4.
Test your understanding by doing the Algebra Checkpoint at the end of this section.
In Section 3.1 we used exponential functions to model exponential growth and decay.
When working with exponential models, we often need to answer questions such as:
How long will it take for a population to reach a given size? How long does it take for a
radioactive sample to decay to 1% of its original size? To answer these questions, we need
to solve exponential equations, and solving such equations requires the use of logarithms.
In this section we’ll see how logarithms allow us to “tame” very large or very
small numbers. For example, the world bird population is estimated at birds, but
the logarithm of is just 11; the mass of an electron is about grams, but the
logarithm of is just . Do you see the pattern?- 2910
-29
10
-29
10
11
10
11
2
■ Logarithms Base 10
The logarithm base 10 (or common logarithm) of a number x is the power to which
we must raise 10 to get x.
Logarithms Base 10
The next example illustrates how to find logarithms of powers of 10.
The world bird population is
about ; the logarithm of
is just 11.10
11
10
11
The logarithm base 10 of x is defined by
We read as “log base 10 of x.” Logarithms base 10 are called
common logarithms, and is often written simply as (omitting
the subscript 10).
log xlog
10
x
log
10
x
log
10
x = yif and only if10
y
= x
From this definition we see that the logarithm of a positive number x is an ex-
ponent: “ is the exponent to which we must raise 10 to get x.” So if x is a power
of 10, it’s easy to find . In fact, . The following table shows the
pattern for finding logarithms.
log
10
10
x
= xlog
10
x
log
10
x
x
10
-4
10
-3
10
-2
10
-1
10
0
10
1
10
2
10
3
10
4
log
10
x
- 4 - 3 - 2 - 1
0 1 2 3 4
Lothar Redlin

SECTION 4.1
■
Logarithmic Functions 325
example
1
Finding Logarithms of Powers of 10
Find the following logarithms.
(a)
(b)
(c)
(d)
Solution
To find the logarithm of a number, it’s helpful to express the number as a power
of 10.
(a)
(b)
(c)
(d)
■ NOW TRY EXERCISE 7 ■
We need to do some additional work to find the logarithms of numbers that are
not easily expressed as powers of 10. To find the logarithm of 735, we need to ex-
press it as a power of 10. In other words, we need to find a number y such that
.735 = 10
y
log
10
110 = log
10
10
1>2
=
1
2
log
10
1
100
= log
10
10
-2
=-2
log
10
1,000,000 = log
10
10
6
= 6
log
10
1000 = log
10
10
3
= 3
log
10
110
log
10
1
100
log
10
1,000,000
log
10
1000
example
2
Finding Logarithms Using a Calculator
The Rules of Exponents are
reviewed in Algebra Toolkits A.3
and A.5, pages T14 and T20.
x (decimal form) 100 735 1000
x (exponential form)
10
2
10
y
10
3
log
10
x 2 y 3
By the definition of the logarithm, the exponent y is precisely . Let’s esti-
mate the value of y. Since , the power to which we need to raise
10 to get 735 is between 2 and 3. That is,
To get a better approximation, we can experiment to find a power of 10 that is closer
to 735. For instance, using a calculator, we find
So is between 2.8 and 2.9. We can continue this process to get better esti-
mates, but fortunately, scientific calculators have a key that gives the values of
base 10 logarithms.
lOG
log
10
735
10
2.7
L 501.210
2.8
L 631.010
2.9
L 794.3
2 6 log
10
735 6 3
100 6 735 6 1000
log
10
735
Find the following logarithms using a calculator.
(a)
(b)
(c)
(d) log
10
110
log
10
0.002
log
10
50
log
10
735

From this definition we see that the logarithm of a positive number x is an ex-
ponent: “ is the exponent to which we must raise a to get x.” So if x is a power
of a, it’s easy to find . In fact, . The following table shows the pat-
tern for finding logarithms base 2.
log
a
a
x
= xlog
a
x
log
a
x
326 CHAPTER 4
■
Logarithmic Functions and Exponential Models
Solution
Calculator Keystrokes Output
(a) 2.866287339
(b) 1.698970004
(c)
(d) 0.5
■ NOW TRY EXERCISE 9 ■
An ant is a lot smaller than an elephant, which in turn is a lot smaller than a
whale. Let’s find the logarithms of the weights of these animals.
ENTER01
2
lOG
log
10
210
- 2.698970004
ENTER200.lOG
log
10
0.002
ENTER05lOG
log
10
50
ENTER537lOG
log
10
735
example
3
Finding Logarithms
The weights of a particular ant, elephant, and whale are given. Find the logarithms
of these weights.
Ant 0.000003 kilograms
Elephant 4000 kilograms
Whale 170,000 kilograms
Solution
We use a calculator to find the logarithms.
Ant
Elephant
Whale
■ NOW TRY EXERCISE 11 ■
log 170,000 L 5.2
log 4000 L 3.6
log 0.000003 L-5.5
2
■ Logarithms Base a
Recall that log x is the common
logarithm, which is the same as
.log
10
x
To analyze exponential growth models with growth factor a, we need logarithms base
a. These are defined in exactly the same way that we’ve defined logarithms base 10.
Logarithms Base a
If a is a positive number then the logarithm base a of x is defined by
We read as “log base a of x.”log
a
x
log
a
x = yif and only ifa
y
= x

SECTION 4.1
■
Logarithmic Functions 327
example
4
Finding Logarithms for Different Bases
Find the following logarithms.
(a) (b) (c) (d)
Solution
To find the logarithm of a number, it’s helpful to express the number as a power of
the base.
(a)
(b)
(c)
(d)
■ NOW TRY EXERCISE 17 ■
From the definition of logarithms we see that there are two equivalent ways of
expressing the relationship between a number and its logarithm: the logarithmic
form and the exponential form . In switching back and forth be-
tween the logarithmic form and exponential form, it is helpful to notice that in each
form, the base is the same:
Logarithmic form Exponential form
Exponent Exponent
TT
cc
Base Base
a
y
= xlog
a
x = y
a
y
= xlog
a
x = y
log
16
4 = log
16
116 = log
16
16
1>2
=
1
2
log
3
1
9
= log
3
3
-2
=-2
log
5
25 = log
5
5
2
= 2
log
2
32 = log
2
2
5
= 5
log
16
4log
3
1
9
log
5
25log
2
32
x
2
-4
2
-3
2
-2
2
-1
2
0
2
1
2
2
2
3
2
4
log
2
x
- 4 - 3 - 2 - 1
0 1 2 3 4
The next example illustrates how to find logarithms for different bases.
example
5
Logarithmic and Exponential Forms
The logarithmic and exponential forms are equivalent equations; if one is true, so is
the other. So we can switch from one form to the other.
Logarithmic form Exponential form
■ NOW TRY EXERCISE 27 ■
5
1
= 5log
5
5 = 1
5
-1
=
1
5
log
5
1
5
=-1
9
1>2
= 3log
9
3 =
1
2
2
-3
=
1
8
log
2
1
8
=-3
2
3
= 8log
2
8 = 3
10
5
= 100,000log 100,000 = 5

328 CHAPTER 4
■
Logarithmic Functions and Exponential Models
2
■ Basic Properties of Logarithms
example
6
Applying the Basic Properties of Logarithms
Evaluate the expression.
(a) (b) (c) (d)
Solution
We use the basic properties of logarithms to evaluate the expressions.
(a) Property 1
(b) Property 2
(c) Property 3
(d) Property 4
■ NOW TRY EXERCISES 15 AND 21 ■
5
log
5
12
= 12
log
2
2
15
= 15
log
3
3 = 1
log
8
1 = 0
5
log
5
12
log
2
2
15
log
3
3log
8
1
Property Reason
1. We raise a to the exponent 0 to get 1.
2. We raise a to the exponent 1 to get a.
3. We raise a to the exponent x to get .
4. is the exponent to which a must be raised to get x.log
a
xa
log
a
x
= x
a
x
log
a
a
x
= x
log
a
a = 1
log
a
1 = 0
2
■ Logarithmic Functions and Their Graphs
Recall that a function is a rule f that assigns a number to each number x in the
domain of f. The logarithmic function with base a is defined as follows.
Logarithmic Functions
f 1x2
The logarithmic function with base a is the function
where and . The domain of f is .10, q 2a ⫽ 1a 7 0
f 1x2= log
a
x
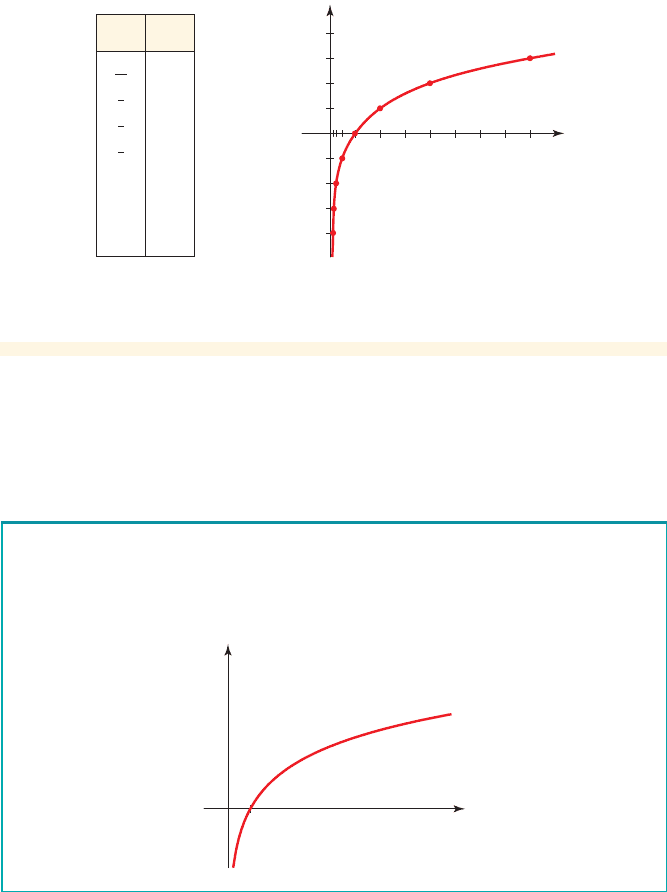
example
7
Graphing Logarithmic Functions
Graph the logarithmic function .f 1x 2= log
2
x
From the definition of logarithms we can establish the following basic properties.
Basic Properties of Logarithms
SECTION 4.1
■
Logarithmic Functions 329
x
f 1x 2
1
16
- 4
1
8
- 3
1
4
- 2
1
2
- 1
1 0
2 1
4 2
8 3
x
y
1
2
3
4
12 4 6 8
_1
_2
_3
_4
f(x)=log¤ x
figure 1 Graph of f 1x 2= log
2
x
The graph of the logarithmic function for has the
following general shape. The line (the y-axis) is a vertical asymptote
of f.
x = 0
a 7 1f 1x 2= log
a
x
x
y
0
f(x)=
1
log
a
x
Solution
example
8
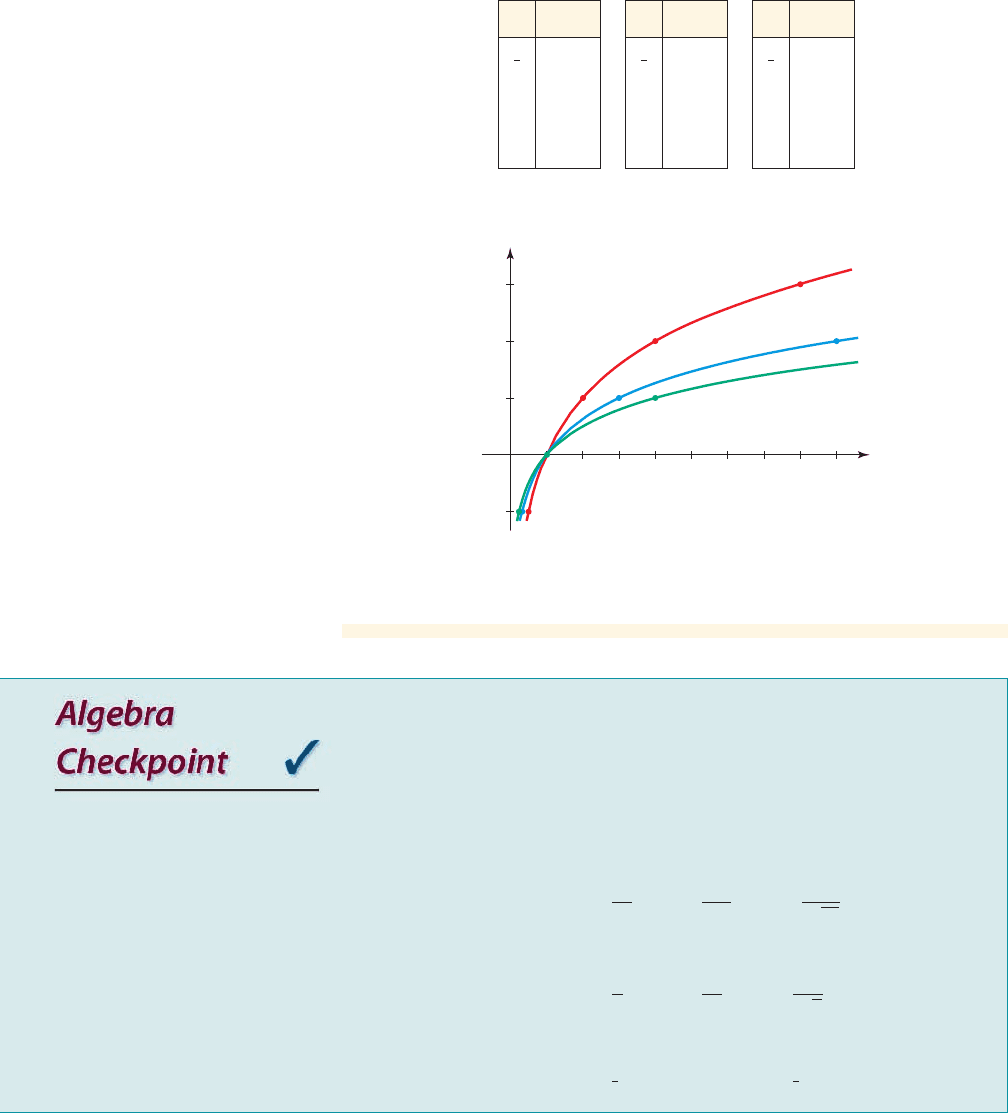
Graphing a Family of Logarithmic Functions
Graph the family of logarithmic functions for . Explain how
changing the value of a affects the graph.
a = 2, 3, 4f 1x 2= log
a
x
To make a table of values, we choose the x-values to be powers of 2 so that we can
easily find their logarithms. Then we plot the points in the table and connect them
with a smooth curve as in Figure 1.
■ NOW TRY EXERCISE 41 ■
Logarithmic functions with base greater than 1 all have the same basic shape as
the one in Example 7.
Graphs of Logarithmic Functions
330 CHAPTER 4
■
Logarithmic Functions and Exponential Models
Check your knowledge of the rules of exponents by doing the following prob-
lems. You can review the rules of exponents in
Algebra Toolkits A.3
and
A.4
on
pages T14 and T20.
1. Evaluate each expression without using a calculator.
(a) (b) (c) (d) (e)
2. Express each number as a power of 10.
(a) 100 (b) 10,000 (c) (d) (e)
3. Express each number as a power of 2.
(a) 16 (b) 64 (c) (d) (e)
4. Express each number as a power of 9.
(a) 81 (b) 729 (c) (d) 3 (e)
1
3
1
9
1
1
3
2
1
16
1
2
1
110
1
100
1
10
27
-1>3
4
1>2
5
-2
5
-1
4
3
The graphs are shown in Figure 2 for x-values between 0 and 9.
x
y
1
2
3
12 4 6 83579
0
_1
y=log‹ x
y=log› x
y=log¤x
figure 2 A family of logarithmic
functions
Solution
We plot points as an aid to sketching these graphs. In each case we choose the x-values
to be powers of the base so that we can easily find their logarithms.
x log
2
x
1
2
- 1
1 0
2 1
4 2
8 3
x log
3
x
1
3
- 1
1 0
3 1
9 2
27 3
x log
4
x
1
4
- 1
1 0
4 1
16 2
64 3
We notice from these graphs that the logarithmic function increases more slowly for
larger values of the base a.
■ NOW TRY EXERCISE 51 ■
SECTION 4.1
■
Logarithmic Functions 331
4.1 Exercises
CONCEPTS
Fundamentals
1. is the exponent to which the base 10 must be raised to get _______. Use this fact
to complete the following table for .log x
log x
x
10
3
10
2
10
1
10
0
10
-1
10
-2
10
-3
10
1>2
10
3.4
log x
2. (a) , so log ⫽
(b) , so ⫽
3. The function is the logarithm function with base
_______. So
_______, _______, _______, _______, and
_______.
4. Match the function with its graph.
(a) (b) g1x 2= log
6
xf 1x 2= 6
x
f 13 2=
f 181 2=f A
1
9
B=f 11 2=f 192=
f 1x 2= log
9
x
log
5
25 = 2
5
3
= 125
x
y
1
5
III
10 15
0
_1
x
y
10
15
5
1
0
Think About It
5. True or false?
(a) For any , the logarithm function is always increasing.
(b) For any , the graph of the logarithm function has x-intercept 1.
(c) For any , the graph of the logarithm function has y-intercept 1.
6. Use the fact that to give a rough estimate of . Use a
calculator to check your estimate.
7–8
■ Find the given common logarithm.
7. (a) (b) (c) (d)
8. (a) (b) (c) (d)
9–10 ■ Use a calculator to evaluate the given common logarithm.
9. (a) log 132 (b) log 5000 (c) (d) log 0.3
10. (a) log 0.145 (b) log 16 (c) (d) log 750log
1
9
log 12
log
10
0.0001log
10
1log
10
1
110
log
10
1,000,000,000,000
log
10
2
3
10log
10
0.01log
10
1
10
log
10
10,000
log 35001000 6 3500 6 10,000
f 1x 2= log
a
xa 7 1
f 1x 2= log
a
xa 7 1
f 1x 2= log
a
xa 7 1
SKILLS
Logarithmic
form
Exponential
form
4
3
= 64
log
4
2 =
1
2
4
3>2
= 8
log
4
A
1
16
B=-2
log
4
A
1
2
B=-
1
2
4
-5>2
=
1
32
Logarithmic
form
Exponential
form
log
8
8 = 1
log
8
64 = 2
8
2>3
= 4
8
3
= 512
log
8
A
1
8
B=-1
8
-2
=
1
64
332 CHAPTER 4
■
Logarithmic Functions and Exponential Models
11–14
■ Find the logarithm of the given numbers.
11. (a) The diameter of a bacterium: 0.00012 centimeter
(b) The height of a human: 173 centimeters
12. (a) The length of an acorn: 2 centimeters
(b) The height of a fully grown oak tree: 914 centimeters
13. (a) The weight of a hummingbird: 4 grams
(b) The weight of a bald eagle: 5443 grams
14. (a) The radius of the earth: 6378 kilometers
(b) The radius of the sun: 696,000 kilometers
15–26
■ Find the given logarithm.
15. (a) (b) (c)
16. (a) (b) (c)
17. (a) (b) (c)
18. (a) (b) (c)
19. (a) (b) (c)
20. (a) (b) (c)
21. (a) (b) (c)
22. (a) (b) (c)
23. (a) (b) (c)
24. (a) (b) (c)
25. (a) (b) (c)
26. (a) (b) (c)
27–28
■ Fill in the table by finding the appropriate logarithmic or exponential form of the
equation, as in Example 4.
27. 28.
log
4
8log
4
A
1
2
Blog
4
12
log
9
13log
49
7log
5
125
log
5
10.2 2log
10
110log
3
A
1
27
B
log
6
1log
8
8
17
log
2
32
10
log 5
6
log
6
72
9
log
9
18
4
log
4
5
3
log
3
8
2
log
2
37
log
7
7
10
log
9
81log
6
36
log
3
9log
4
64log
5
5
4
log
7
1
49
log
7
49log
7
1
log
4
4log
4
1
4
log
4
16
log
9
9log
9
9
8
log
9
1
log
3
3
2
log
3
1log
3
3
29–32
■ Express the equation in exponential form.
29. (a) (b)
30. (a) (b)
31. (a) (b)
32. (a) (b) log
2
1
8
=-3log
3
81 = 4
log
9
3 =
1
2
log
8
2 =
1
3
log
8
512 = 3log
10
0.1 =-1
log
5
1 = 0log
5
125 = 3
SECTION 4.1
■
Logarithmic Functions 333
33–36 ■ Express the equation in logarithmic form.
33. (a) (b)
34. (a) (b)
35. (a) (b)
36. (a) (b)
37–40
■ Use the definition of the logarithmic function to find x.
37. (a) (b)
38. (a) (b)
39. (a) (b)
40. (a) (b)
41–42
■ Fill in the table and sketch the graph of the function by plotting points.
41. 42. f 1x 2= log
4
xf 1x2= log
3
x
log
x
3 =
1
3
log
x
6 =
1
2
log
4
x = 2log
4
2 = x
log
10
0.1 = xlog
5
x = 4
log
2
16 = xlog
2
x = 5
7
3
= 3434
-3>2
= 0.125
2
-3
=
1
8
8
-1
=
1
8
81
1>2
= 910
3
= 1000
10
-4
= 0.00013
3
= 27
x f(x)
1
27
1
9
1
3
1
3
9
27
x f(x)
1
16
1
4
1
4
16
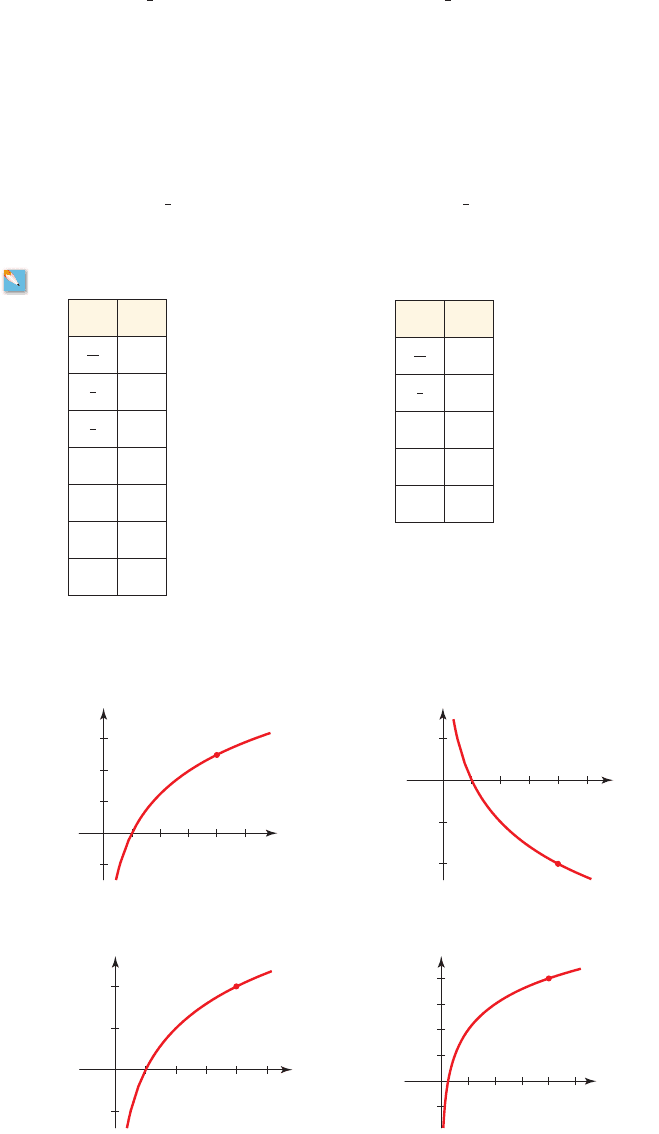
43–46 ■ Match the function with its graph.
43. 44. f 1x 2=-log
4
xf 1x 2= log
4
x
x
y
2
4
6
1
I
25
(4, 5)
43
0
_2
x
y
0.5
1
II
2
(4, _1)
345
0
_1.0
_0.5
45. 46. f 1x 2= 5 log
4
xf 1x2= log
4
4x
(4, 1)
III
_
x
y
1.0
0.5
12345
0
_0.5
(4, 2)
y
0.5
1.0
2.0
1.5
IV
_0.5
x
12345
0
