Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

2. In the introduction to this Exploration we learned that the world’s oceans

contain 6 sextillion cups of water and each cup of water contains

about 24 septillion atoms. How many atoms do the oceans

contain? Express your answer in scientific notation.

3. In 2006 there were approximately 120,000,000 homes in the United States,

and the average home price was $219,000.

(a) Write these numbers in scientific notation.

(b) Multiply these numbers to find the total value of U.S. residential real

estate in 2006.

4. Let’s see how to divide two numbers given in scientific notation.

(a) Divide the following two numbers. To keep your answer in scientific

notation, combine the powers of 10 separately.

(b) Divide the following two numbers and write your answer in scientific

notation. Notice that the number is in scientific notation only if

5. The distance from the earth to the sun is mi and the speed of light is

mi/s. How long does it take light to reach us from the sun?

Convert your answer from seconds to minutes.

6. On January 1, 2007, the U.S. national debt was $8,678,000,000,000, and the

U.S. population was 300,900,000.

(a) Write these numbers in scientific notation.

(b) If the national debt is distributed over the entire population, how much

does each person owe?

= __________ 1decimal notation2

national debt

population

= __________ 1scientific notation 2

population = _______________

national debt = _______________

1.86 * 10

9.3 * 10

2.7 * 10

6.5 * 10

-5

2.7

6.5

-5

= _______ * 10

ⵧ

= _______ * 10

ⵧ

1 … a 6 10

a * 10

8.4 * 10

2.1 * 10

8.4

2.1

= _______ * 10

ⵧ

= ____________________ 1decimal notation 2

number * average price = ___________________ 1scientific notation2

average home price = ___________________

number of homes = ___________________

12.4 * 10

16 * 10

314 CHAPTER 3

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

EXPLORATIONS 315

So You Want to Be a Millionaire?

OBJECTIVE To become familiar with the rapid rate of growth of exponential

functions.

If you want to be a millionaire, you can start by taking Benjamin Franklin’s wise

advice:

“A penny saved is a penny earned.”

But you’re going to have to save more and more pennies each day. So suppose you

put a penny in your piggy bank today, two pennies tomorrow, four pennies the next

day, and so on, doubling the number of pennies you add to the bank each day. Let’s

call the first day we put a penny in the bank Day 0, the next Day 1, and so on. So on

Day 3 you put 8 pennies in the bank, on Day 5 you put in 32 pennies, and on Day 10

you put in 1024 pennies, or about 10 dollars worth of pennies.

This doesn’t seem like an effective way of becoming a millionare; after all,

we’re just saving pennies. How many years does it take to save a million dollars this

way? We’ll work it out in this exploration, and in the process we hope to improve our

intuition for exponential growth.

I. How to Save a Million Dollars

1. (a) Complete the table for the number of pennies saved each day.

Day x 0 1 2 3 4 5

Pennies saved f 1x2

Day x 0 1 2 3 4 5 6 7 8 9

Pennies saved f 1x2

Day x 10 11 12 13 14 15 16 17 18 19

Dollars saved

$1 0

Day x 20 21 22 23 24 25 26 27 28 29

Dollars saved

$10,000

(b) The number of pennies saved each day grows exponentially. What is the

growth factor? What is the initial value? Find an exponential function

that models the number of pennies saved on day x.

2. Let’s complete the table for the number of pennies saved on each day for 30

days, without using a calculator—but we’ll make the calculations easier by

making some approximations. On Day 10 we must save , or 1024 pennies.

Since this is about $10, we’ll write $10 instead of the 1024 pennies. On Day

20 we must save pennies; check that this is approximately $10,000.

f 1x2=

ⵧ

ⴢ

ⵧ

f 1x2= Ca

3. On which day does the amount we put in first exceed one million dollars? Is

your answer surprising? What does this experiment tell us about exponential

growth?

II. How to Manage Population Growth

We know that population grows exponentially. Let’s see what this means for a

type of bacteria that splits every minute. Suppose that at 12:00 noon a single bac-

terium colonizes a discarded food can. The bacterium and its descendents are all

happy, but they fear the time when the can is completely full of bacteria—

doomsday.

1. How many bacteria are in the can at 12:05? At 12:10?

2. The can is completely full of bacteria at 1:00 P.M. At what time was the can

only half full of bacteria?

3. When the can is exactly half full, the president of the bacteria colony

reassures his constituents that doomsday is far away—after all, there is as

much room left in the can as has been used in the entire previous history of

the colony. Is the president correct? How much time is left before

doomsday?

4. When the can is a quarter full, how much time is left till doomsday?

Exponential Patterns

OBJECTIVE To recognize exponential data and find exponential functions that fit

the data exactly.

In Exploration 2 of Chapter 2 (page 233) we discussed the importance of finding pat-

terns, and we found many linear patterns. In this exploration we find exponential pat-

terns. We’ve already learned how exponential functions model interest, population

growth, and other real-world phenomena. But exponential patterns also occur in un-

expected places, as we’ll see in this exploration.

I. Recognizing Exponential Data

To find exponential patterns, we look at the ratio of consecutive outputs of the data.

In this exploration we assume that the inputs are the equally spaced numbers

We want to find properties of the outputs that guarantee that there is an exponential

function that exactly models the data. So let’s consider the exponential function

In the next question we confirm that the entries in Table 1 at the top of the next page

are correct. In particular, the ratio of consecutive terms is constant.

f 1x2= Ca

0,˛ 1,˛ 2,˛ 3,˛ . . .

316 CHAPTER 3

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

EXPLORATIONS 317

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

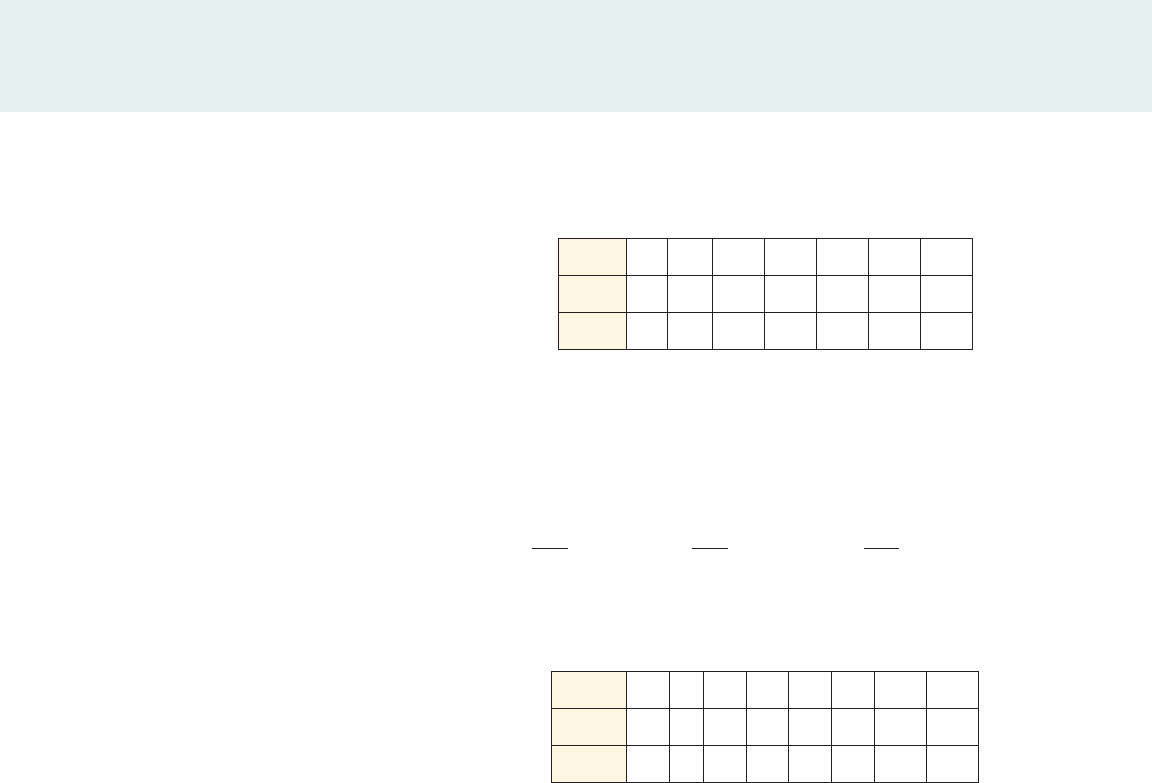
table 1

Ratios of consecutive outputs for f 1x 2= Ca

x 0 1 2 3 4 5 6

f 1x 2

C Ca

Ratio — a a a a a a

1. (a) Find the outputs of the exponential function corresponding to

the inputs 0, 1, 2, 3, . . . .

,,,

(b) Use your answers to part (a) to find the ratio between consecutive terms.

2. A data set is given in the table.

f 132

f 122

___________

f 122

f 112

___________

f 112

f 102

= _______

f 132= _______f 122= _______f 112= _______f 102= _______C

f 1x 2= Ca

(a) Fill in the entries for the ratios of consecutive outputs.

(b) Observe that the ratios of consecutive terms are constant, so there is an

exponential function that models the data. To find C and a,

let’s compare the entries in this table with those of Table 1. Comparing the

output corresponding to the input 0 in each of these tables, we conclude

that

Comparing the ratios in each of these tables, we conclude that

So an exponential function that models the data is

match the values in the table.

II. Exponential Patterns

1. A person has two parents, four grandparents, eight great-grandparents, and

so on.

f 102, f 112, f 122, . . .

f 1x2=

ⵧ

ⴢ

ⵧ

a = _______

C = _______

f 1x2= Ca

x 0 1 2 3 4 5 6 7

f 1x 2

3 6 12 24 48 96 192 384

Ratios —

(a) Complete the table below for the number of ancestors a person has x

generations back, and then calculate the ratio of consecutive outputs.

(b) Are the ratios of consecutive outputs constant? If so, find C and a by com-

paring the entries in this table with the corresponding entries in Table 1.

Find an exponential function that models the pattern in the data:

f 1x2=

ⵧ

ⴢ

ⵧ

C = ________a = ________

Generation x 0 1 2 3 4

Number of ancestors f 1x 2

1 2

Ratio

—

(b) Are the ratios of consecutive outputs constant? Is there an exponential

pattern relating the generation and the number of ancestors? If so, find C

and a by comparing the entries in this table with the corresponding entries

in Table 1.

An exponential function that models the pattern in the data is:

back? Why might there actually be fewer ancestors than the number the

model predicts 15 generations back?

2. When a particular ball is dropped, it bounces back up to one-third of the

distance it has fallen. The ball is dropped from a height of 2 meters.

(a) Complete the table for the height the ball reaches on bounce x, and then

calculate the ratio of consecutive outputs.

f 1x2= _______

C = _______

a = _______

123

2 m

Bounce x 1 2 3 4 5

Height f 1x 2 2>3

Ratio

—

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

318 CHAPTER 3

Father

Mother

Grandfather

Grandmother

Grandfather

Grandmother

Sta

e 1 Sta

e 2 Sta

e 3

Stage x 1 2 3 4

Number of blue squares added, f 1x2

Ratio —

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

EXPLORATIONS 319

(a) Complete the table for the number of blue squares added at stage x, and

then calculate the ratio of consecutive outputs.

(b) Are the ratios of consecutive outputs constant? If so, find C and a by

comparing the entries in this table with the corresponding entries in

Table 1.

Find an exponential function that models the pattern in the data:

(d) Complete the table for the area of each of the blue squares added at stage

x, then calculate the ratio of consecutive outputs.

f 1x2= _______________

C = _______

a = _______

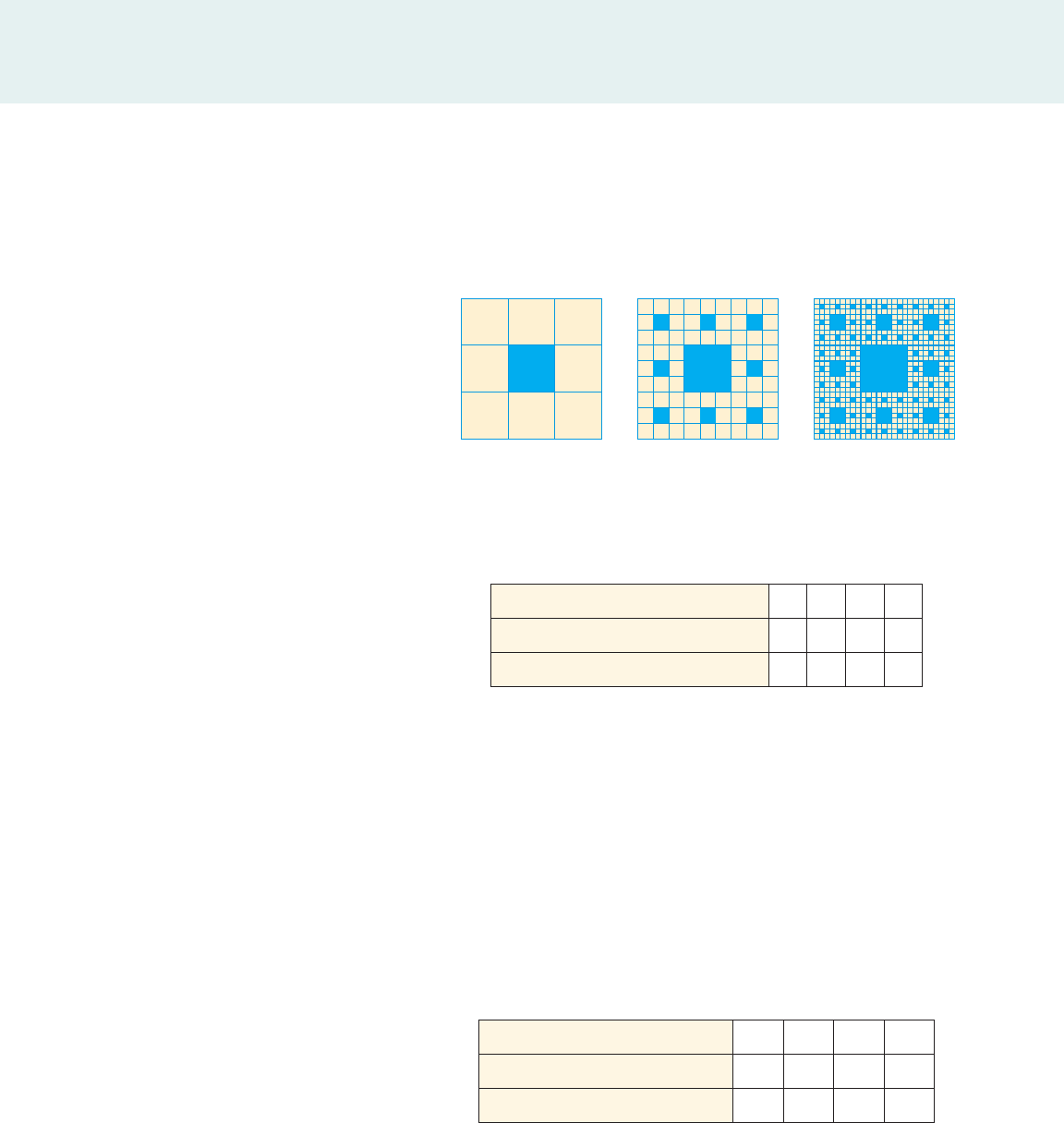
3. A yellow square of side 1 is divided into nine smaller squares, and the middle

square is colored blue as shown in the figure. Each of the smaller yellow

squares is in turn divided into nine squares, and each middle square is colored

blue.

Stage x 1 2 3 4

Area of blue squares added, A1x 2 1>9

Ratio —

(e) Find an exponential function that models the area of each blue square

added at stage x.

A 1x2= _______________

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

320 CHAPTER 3

Modeling Radioactivity with Coins and Dice

OBJECTIVE To experience how random events can lead to exponential decay models.

Radioactive elements decay when their atoms spontaneously emit radiation and

change into smaller, stable atoms. But if atoms decay randomly, how is it possible to

find a function that models their behavior? We’ll try to answer this question by ex-

perimenting with coins and dice.

Imagine tossing a coin 100 times (or, equivalently, tossing 100 coins all at once).

How often would you expect to get 100 heads? Or 99 heads? A much more likely out-

come is that the number of heads and tails will be about the same (because the “rate” at

which heads appears is 50%). So although the outcome of a single toss of a coin is totally

unpredictable, when we toss many coins, the number of heads is fairly predictable. Of

course, there are a lot more than 100 atoms in even the tiniest sample of a radioactive sub-

stance, so the outcome of the random decay of atoms in the sample is quite predictable.

Let’s simulate the random decay of radioactive atoms using coin tosses and rolls of dice.

I. Modeling Radioactive Decay with Coins

In this first experiment we toss pennies to simulate the decay of atoms in a radioac-

tive substance.

You will need:

■

40 pennies

■

A cup or jar

■

A table

Procedure:

1. Put the pennies in a cup and shake them well, then toss them on a table. The

pennies that show tails are considered “decayed,” and those that show heads

are still “radioactive.”

2. Discard the decayed pennies and collect the radioactive ones. Record the

number of radioactive pennies remaining (in the table below).

3. Repeat Steps 1 and 2 with the remaining radioactive pennies until all the

pennies have decayed.

Toss

number

Pennies

remaining

f 1x 2

Ratio

f 1x ⴙ 12

f 1x 2

—

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

EXPLORATIONS 321

Analysis:

4. Is an exponential model appropriate for the data you obtained? To decide,

complete the “Ratio” column in the table to determine whether there is a

reasonably constant “decay factor.”

5. (a) Use the ExpReg command on a graphing calculator to find the exponen-

tial curve that best fits the data:

(b) What is the decay factor for the model you found in part (a)? Is the decay

factor what we should expect when tossing pennies?

II. Modeling Radioactive Decay with Dice

In this experiment we roll dice to simulate the decay of atoms in a radioactive substance.

You will need:

■

24 dice

■

A cup or jar

■

A table

Procedure:

This is basically the same experiment as in Part I, except with dice.

1. Put the dice in a cup and shake them well, then roll them on a table. The dice

that show a one or a six are considered “decayed,” and the others are still

“radioactive.”

2. Discard the decayed dice and collect the radioactive ones. Record the number

of radioactive dice remaining (in the table below).

3. Repeat Steps 1 and 2 with the remaining radioactive dice until all the dice

have decayed.

Y =

ⵧ

ⴢ

ⵧ

Y = a

Toss

number

Pennies

remaining

f 1x 2

Ratio

f 1x ⴙ 12

f 1x 2

—

Analysis:

4. Is an exponential model appropriate for the data you obtained? To decide,

complete the “Ratio” column in the table to determine whether there is a

reasonably constant “decay factor.”

5. (a) Use the ExpReg command on a graphing calculator to find the exponen-

tial curve that best fits the data:

(b) What is the decay factor for the model you found in part (a)? Is the decay

factor what we should expect when rolling dice?

Y =

ⵧ

ⴢ

ⵧ

Y = a

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

322 CHAPTER 3

323

Are we there yet? It’s a basic question: When will we reach our destination?

In Chapter 3 we modeled the growth of an investment and the growth of a

population using exponential functions. The growth of an investment may

seem frustratingly slow, whereas population growth can be shockingly fast. So

we want to answer questions such as these: When will my bank account have a

million dollars? When will the population reach a given level? If population

continues to grow exponentially (or logistically), when will every street be as

crowded as the New York City street shown in the photo above? These are

important questions that can help us to plan for the future. To answer such

questions, we need to solve exponential equations (equations in which the

unknown is in the exponent), and to do this, we need logarithms. We’ll see

how logarithms allow us to reverse the rule of an exponential function, which

in turn helps us to answer the questions posed here.

4.1 Logarithmic Functions

4.2 Laws of Logarithms

4.3 Logarithmic Scales

4.4 The Natural Exponential

and Logarithm Functions

4.5 Exponential Equations:

Getting Information from

a Model

4.6 Working with Functions:

Composition and Inverse

EXPLORATIONS

Super Origami

2 Orders of Magnitude

3 Semi-Log Graphs

4 The Even-Tempered Clavier

Logarithmic Functions

and Exponential Models

George Marks/Retrofile/Getty Images