Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

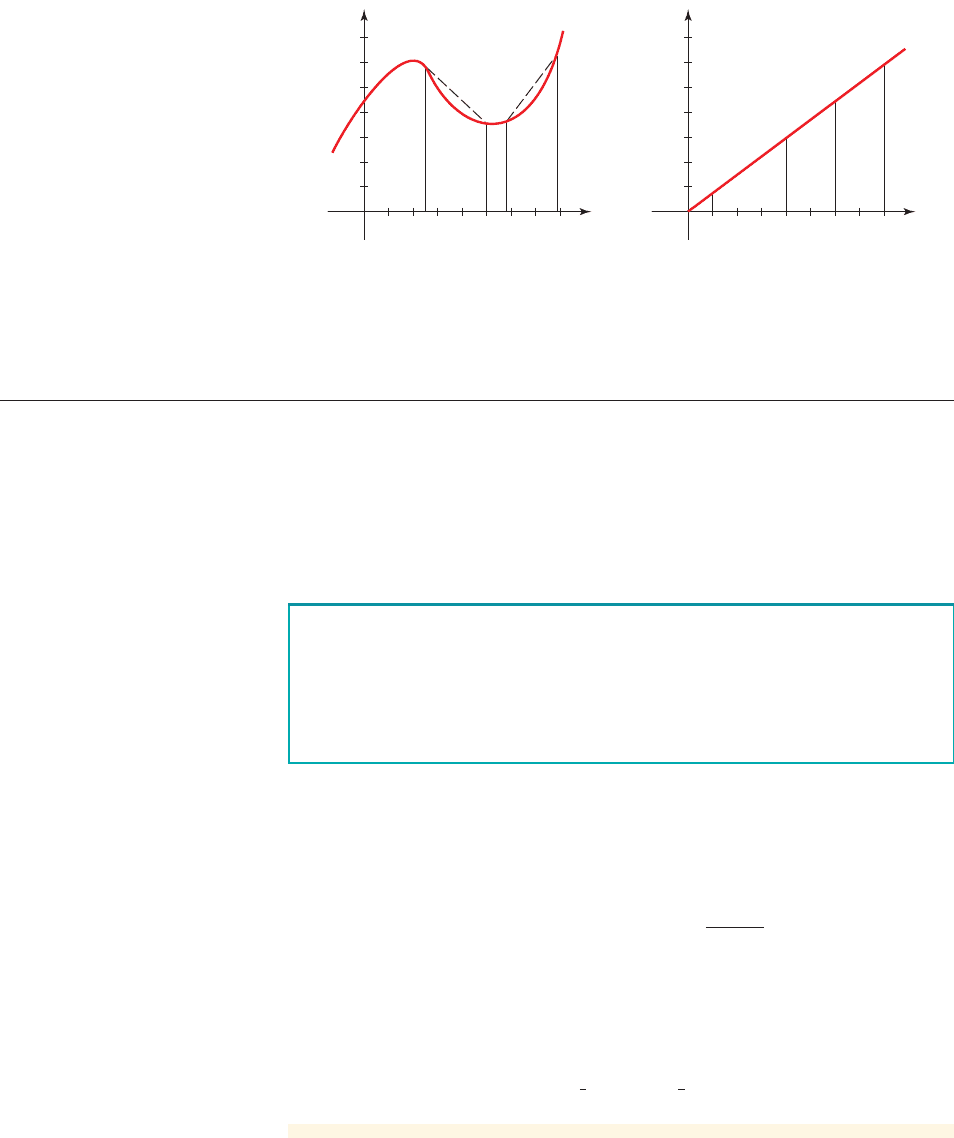
154 CHAPTER 2

■

Linear Functions and Models

■ Linear Functions

In Section 1.3 we encountered functions that have constant rate of change, and we’ve

worked with such functions both numerically and graphically. In fact, the graphs of

functions with constant rate of change are lines. Algebraically, functions with con-

stant rate of change are linear in the following sense.

example

Identifying Linear Functions

Determine whether the following functions are linear.

(a) (b)

Solution

(a) f is a linear function, where b is 2 and m is 3.

(b) is a linear function, where b is 1 and m is .

(d) k is a linear function where b is and m is .

■ NOW TRY EXERCISES 9 AND 11 ■

- 2g

k 1x2=

1 - 5x

h 1x2= 3x

+ 1

g1x 2=-2x + 1f 1x2= 2 + 3x

100

(a) g has different average rates of

change on different intervals.

100

(b) f has the same average rate of

change on every interval.

figure 1

■

A linear function is a function of the form

where b and m are real numbers.

■

The graph of a linear function is a line.

f 1x2= b + mx

Linear Functions

as it attempts to produce chocolates. Notice that the graph of a function that has con-

stant rate of change on every interval is a line.

SECTION 2.2

■

Linear Functions: Constant Rate of Change 155

example

Graphing a Linear Function

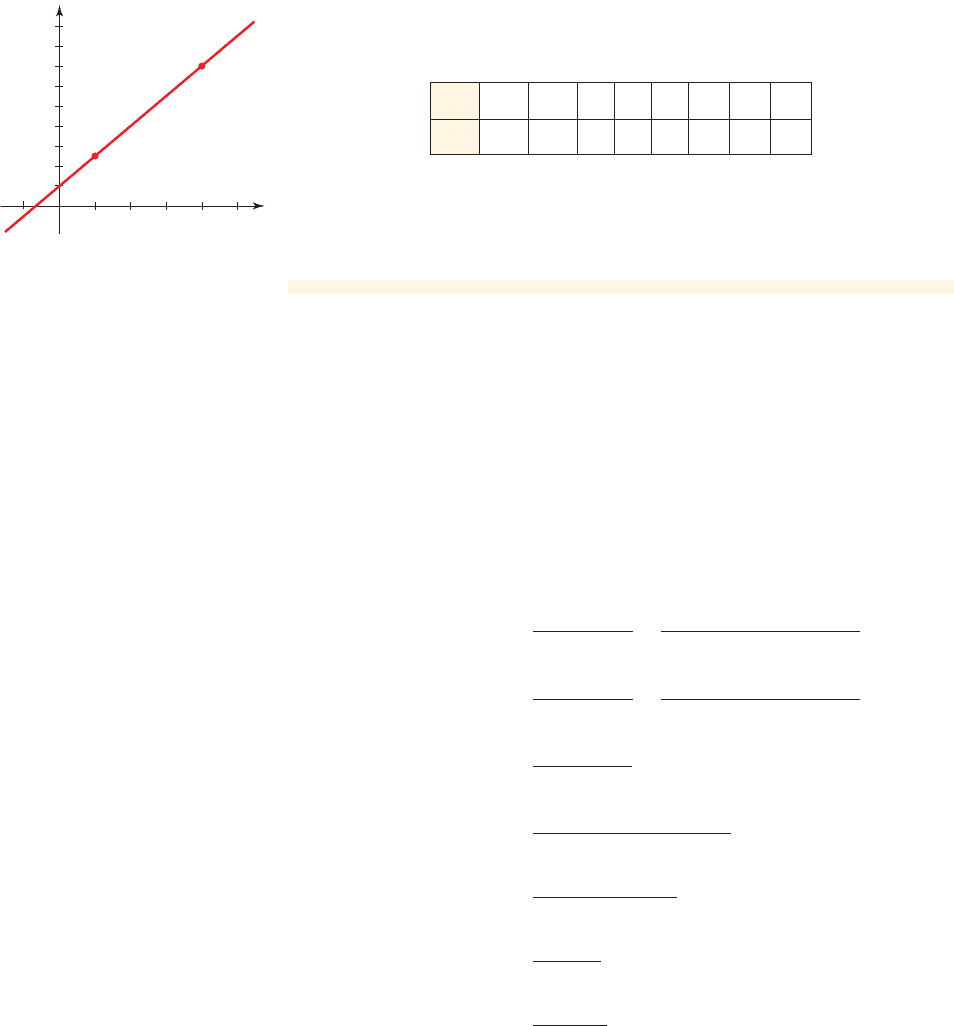
Let f be the linear function ,

(a) Make a table of values of f.

(b) Sketch a graph of f.

Solution

(a) A table of values is shown below.

f 1x 2= 2 + 3x

- 2 - 1

0123 4 5

f(x)

- 4 - 1

2 5 8 11 14 17

(1, 5)

(4, 14)

figure 2 Graph of the linear

function f 1x 2= 2 + 3x

(b) Since f is a linear function its graph is a line. So to obtain the graph of f, we

plot any two points from the table and connect them with a straight line. The

graph is shown in Figure 2.

■ NOW TRY EXERCISE 17 ■

example

Average Rate of Change of a Linear Function

Let f be the linear function . Find the average rate of change on the

following intervals.

(a) Between x ⫽ 0 and x ⫽ 1

(b) Between x ⫽ 1 and x ⫽ 4

What conclusion can you draw from your answers?

Solution

(a)

(b)

Use

Expand

Simplify numerator

Factor 3

Cancel common factor

= 3

31d - c2

d - c

3d - 3c

d - c

2 + 3d - 2 - 3c

d - c

f 1x 2= 2 + 3x =

12 + 3

d2- 12 + 3

d - c

average rate of change =

f 1d 2- f 1c2

d - c

average rate of change =

f 16 2- f 112

6 - 1

12 + 3

62- 12 + 3

= 3

average rate of change =

f 11 2- f 102

1 - 0

12 + 3

12- 12 + 3

= 3

f 1x2= 2 + 3x

156 CHAPTER 2

■

Linear Functions and Models

■ Linear Functions and Rate of Change

In Example 3 we saw that the average rate of change of a linear function is the same

between any two points. In fact, for any linear function the average

rate of change between any two points is the constant m. For this reason, when deal-

ing with linear functions, we refer to the average rate of change as simply the rate of

change. We also call the number b the initial value of f. Of course, ; in

many applications we can think of b as the “starting value” of the function (see

Section 1.3).

b = f 102

f 1x 2= b + mx

example

Linear Model of Growth

Toddlers generally grow at a constant rate. Little Jason’s height between his first and

second birthdays is modeled by the function

where is measured in inches and x is the number of months since his first

birthday.

(a) Is h a linear function?

(b) Make a table of values for h.

(d) At what rate is Jason growing?

(e) Sketch a graph of h.

Solution

(a) Yes, h is a linear function for which b is 25.0 and m is 0.4.

(b) A table of values is shown in the margin.

his first birthday was 25.0 in.

(d) Since h is a linear function its rate of change is the constant m, which in this

case is 0.4. This means that Jason grows 0.4 inch per month. Notice how the

table of values agrees with this observation.

h 1x2

h 1x2= 25.0 + 0.4x

Initial Rate of

value change

f 1x 2= b

+ m

Let f be the linear function .

■

The rate of change of f is the constant m.

■

The initial value of f is the constant b.

f 1x 2= b + mx

Month

Height

h(x) (in.)

0 25.0

1 25.4

2 25.8

3 26.2

4 26.6

5 27.0

6 27.4

7 27.8

8 28.2

9 28.6

10 29.0

11 29.4

12 29.8

Linear Functions and Rate of Change

It appears that the average rate of change is always 3 for this function. In fact, part

x ⫽ c and x ⫽ d is 3.

■ NOW TRY EXERCISE 21 ■

SECTION 2.2

■

Linear Functions: Constant Rate of Change 157

Height

(in.)

246

81012

Month

figure 3 Graph of h 1x 2= 25.0 + 0.4x

■ NOW TRY EXERCISE 53 ■

example

Finding a Linear Model from a Rate of Change

Water is being pumped into a swimming pool at the rate of 5 gal/min. Initially, the

pool has 200 gallons of water. Find a linear function that models the volume of wa-

ter in the pool at any time.

Solution

We need to find a linear function

that models the volume of water in the pool at time t. The rate of change of

volume is 5 gal/min, so . Since the pool has 200 gallons to begin with, we

have . So the initial value is . Now that we know m and b, we

can write

■ NOW TRY EXERCISE 55 ■

V1t 2= 200 + 5t

b = 200V10 2= 200

m = 5

V1t 2

V1t 2= b + mt

■ Linear Functions and Slope

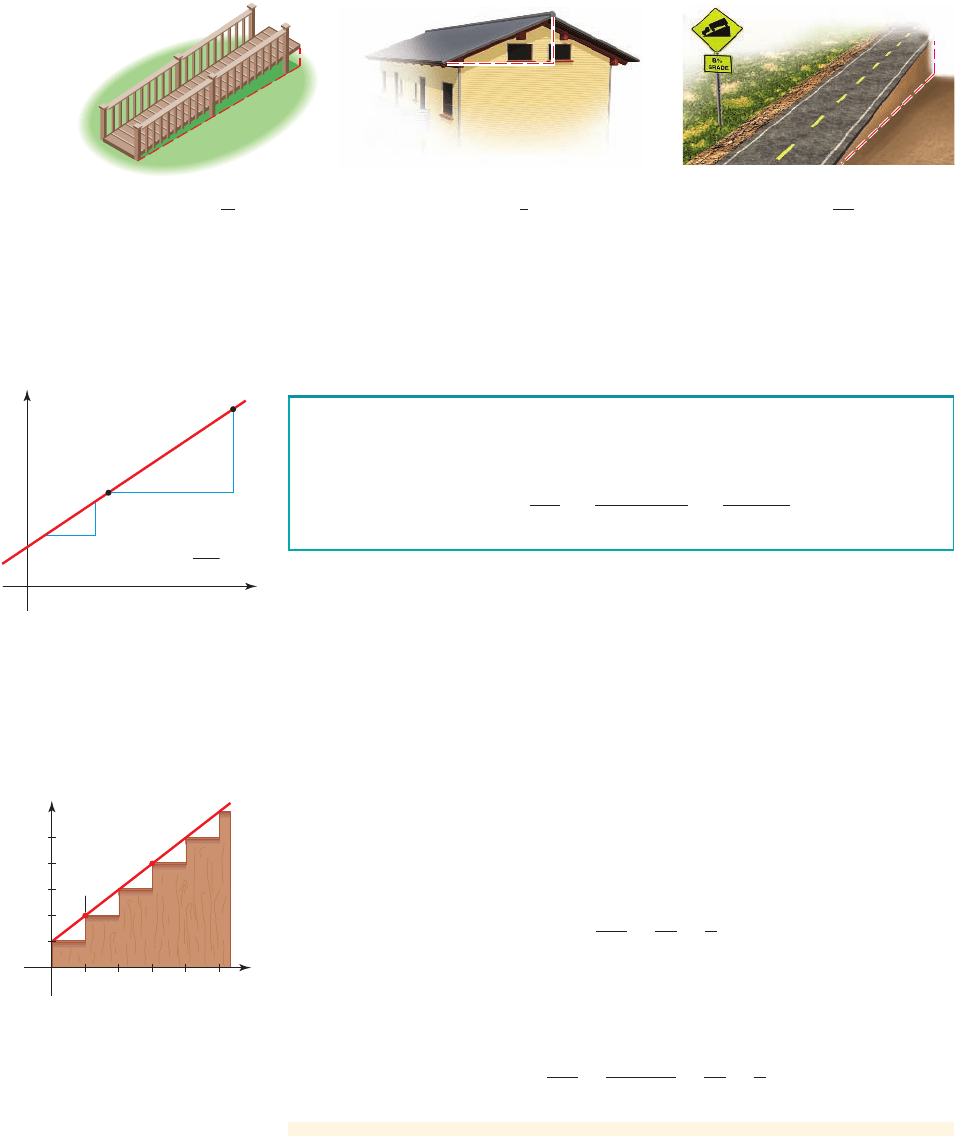
An important property of a line is its “steepness,” or how quickly it rises or falls as

we move along it from left to right. If we move between two points on a line, the run

is the distance we move from left to right, and the rise is the corresponding distance

that we move up (or down). The slope of a line is the ratio of rise to run:

Figure 4 on page 158 shows some situations in which slope is important in real life

and how it is measured in each case. Builders use the term pitch for the slope of a

roof. The uphill or downhill slope of a road is called its grade.

slope =

rise

run

There are 200 gallons of water in

the pool at time . t = 0

(e) Since h is a linear function, its graph is a straight line. So to graph h, we can

plot any two points in the table and connect them with a straight line. See

Figure 3.

158 CHAPTER 2

■

Linear Functions and Models

The graph of a linear function is a line. In this case the run is

the change in the x-coordinate, and the rise is the corresponding change in the

y-coordinate. The slope of a line is the ratio of rise to run.

Slope of a Line

f 1x2= mx + b

Slope of a ramp Pitch of a roof Grade of a road

Slope=

100

figure 4

If and are different points on a line graphed in a coordinate

plane, then the slope of the line is defined by

slope ⫽

rise

run

⫽

change in y

change in x

⫽

⫺ y

⫺ x

, y

21x

, y

From the similar triangles property in geometry it follows that the ratio of rise

to run is the same no matter which points we pick, so the slope is independent of the

points we choose to measure it (see Figure 5).

ris

rise

run

rise

run

slope=

(x⁄, y⁄)

(x¤, y¤)

figure 5 The slope of a line

example

Finding the Slope of a Staircase

In Figure 6 we’ve placed a staircase in a coordinate plane, with the origin at the bot-

tom left corner. The red line in the figure is the edge of the trim board of the stair-

case. Find the slope of this line.

Solution 1

We observe that each of the steps is 8 inches high (the rise) and 12 inches deep (the

run), so the slope of the line is

Solution 2

From Figure 6 we see that two points on the line are (12, 16) and (36, 32). So from

the definition of slope we have

■ NOW TRY EXERCISE 57 ■

For any linear function , the slope of the graph of f is the con-

stant m and the y-intercept is . So we have the following description of the

graph of a linear function.

f 10 2= b

f 1x 2= b + mx

slope =

rise

run

32 - 16

36 - 12

slope =

rise

run

(12, 16)

12 24 36 48 60

(36, 32)

x (in.)

(in.)

figure 6 Slope of a staircase

SECTION 2.2

■

Linear Functions: Constant Rate of Change 159

example

Finding the Slope of a Line

Let f be the linear function .

(a) Sketch the graph of f.

(b) Find the slope of the graph of f.

Solution

(a) The graph of f is a line. To sketch the graph, we need only find two points on

the line. Since and , two points on the graph are

Sketching these points and connecting them by a straight line, we get the

graph in Figure 7.

(b) Since , we see that , so the graph of f is a line with slope

1. We can also find the slope using the definition of slope and the two points

we found in part (a):

So the graph of f is a line with slope 1.

f is 1. We can also calculate the rate of change directly. Using the two values

of the function we found in part (a), we have

■ NOW TRY EXERCISE 25 ■

rate of change =

f 11 2- f 102

1 - 0

3 - 2

= 1

slope =

rise

run

3 - 2

1 - 0

= 1

m = 1f 1x2= 2 + 1ⴢ x

10, 22and11, 3 2

f 11 2= 3f 10 2= 2

f 1x 2= 2 + x

123

figure 7 Graph of f 1x 2= 2 + x

y-intercept Slope

f 1x 2= b

+ mx

■ Using Slope and Rate of Change

For the linear function f in Example 7 we found that the rate of change of f is the

same as the slope of the graph of f. This is true for any linear function. In fact if

and are two different values for x, let’s put and . Then the

points and are on the graph of f. From the definitions of slope and rate

of change we have

We summarize this very useful observation.

slope ⫽

⫺ y

⫺ x

⫽

f 1x

2⫺ f 1x

⫺ x

⫽ rate of change

, y

21x

, y

= f 1x

Let f be the linear function .

■

The graph of f is a line with slope m.

■

The y-intercept of the graph of f is the constant b.

f 1x 2= b + mx

Linear Functions and Slope

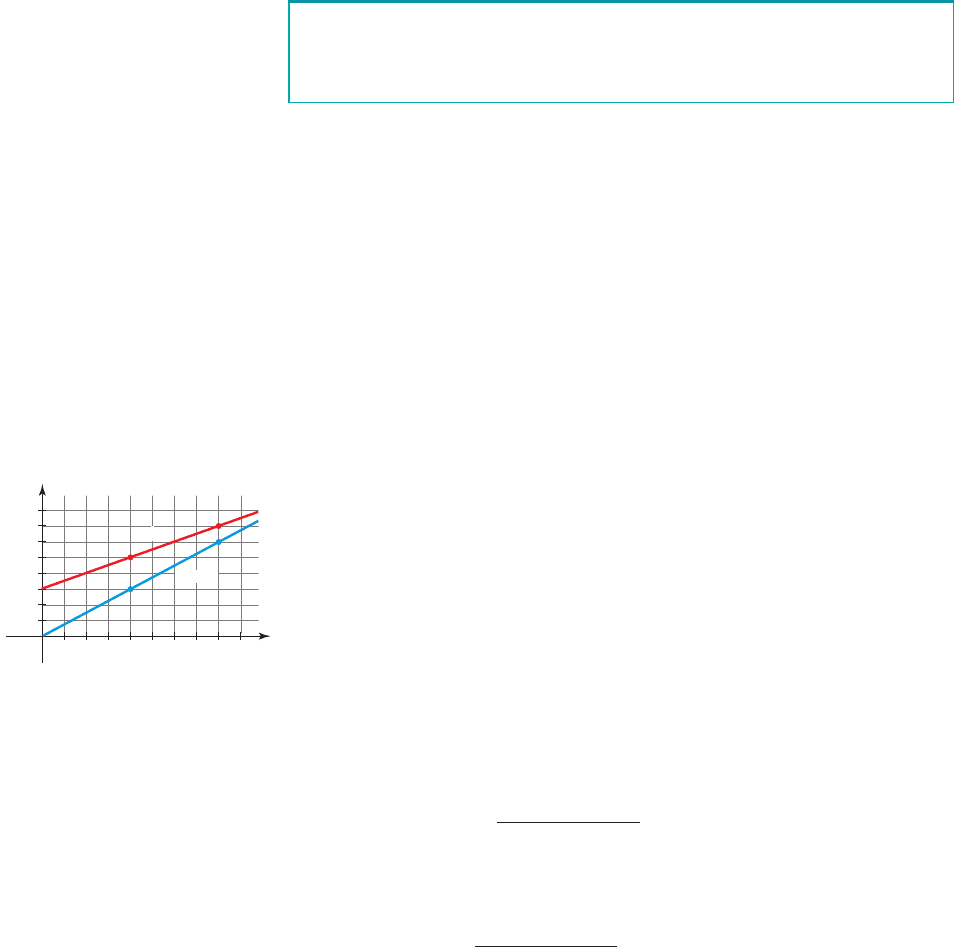
160 CHAPTER 2

■

Linear Functions and Models

The difference between “slope” and “rate of change” is simply a difference in

point of view.

■

For the staircase in Example 6 we prefer to think that the trim board has a

slope of 2>3, although we can also think of the rate of change in the height

of the trim board as 2>3 (the trim board rises 2 inches for each 3-inch

change in the run).

■

For the swimming pool in Example 5 it is more natural to think that the rate

of change of volume is 5 gal/min, although we can also view 5 as being the

slope of the graph of the volume function (the graph rises 5 gallons for

every 1-minute change in time).

example

Finding Linear Functions from a Graph

John and Mary are driving westward along I-76 at constant speeds. The graphs in

Figure 8 show the distance y (in miles) that they have traveled from Philadelphia at

time x (in hours), where x ⫽ 0 corresponds to noon.

(a) At what speeds are John and Mary traveling? Who is traveling faster, and how

does this show up in the graph?

(b) Express the distances that John and Mary have traveled as functions of x.

Solution

(a) From the graph we see that John has traveled 250 miles at 2:00 P.M. and 350

miles at 4:00 P.M. The speed is the rate of change, which is the slope of the

graph, so John’s speed is

/h John’s speed

Mary has traveled 150 miles at 2:00 P.M. and 300 miles at 4:00 P.M., so we

calculate Mary’s speed to be

/h Mary’s speed

(b) Let be the distance John has traveled at time x. We know that f is a linear

function, since the speed (average rate of change) is constant, so we can write

f in the form

In part (a) we showed that m is 50, and from the graph we see that the

y-intercept of John’s graph is . So the distance John has traveled at

time x is

John’s distance

f 1x2= 150 + 50x

b = 150

f 1x2= b + mx

f 1x 2

slope =

300 mi - 150 mi

4 h - 2 h

= 75 mi

slope =

350 mi - 250 mi

4 h - 2 h

= 50 mi

For the linear function we have

slope = rate of change = m

f 1x 2= b + mx

Slope and Rate of Change

100

200

300

400

123

Mary

John

figure 8 John and Mary’s trip

SECTION 2.2

■

Linear Functions: Constant Rate of Change 161

Similarly, Mary is traveling at mi/h, and the y-intercept of her graph is

, so the distance she has traveled at time x is

Mary’s distance

John has traveled

and Mary has traveled

■ NOW TRY EXERCISE 59 ■

g15 2= 7515 2= 375 miles

f 15 2= 150 + 50152= 400 miles

g1x 2= 75x

b = 0

m = 75

2.2 Exercises

CONCEPTS

Fundamentals

1. Let f be a function with constant rate of change. Then

(a) f is a

_______ function.

(b) f is of the form .

______________.

2. Let f be the linear function .

(a) The rate of change of f is

_______, and the initial value is _______.

(b) The graph of f is a

_______, with slope _______ and y-intercept _______.

3. We find the “steepness,” or slope, of a line passing through two points by dividing the

difference in the

____-coordinates of these points by the difference in the ____-

coordinates. So the line passing through the points (0, 1) and (2, 5) has slope

4. The graph of a linear function f is given in the margin. The y-intercept of f is

_______,

the slope of the graph of f is

_______, and the rate of change of f is _______.

ⵧ

= ________

f 1x 2= 7 - 2x

f 1x 2=

ⵧ

Think About It

5. Which of the following functions is not linear? Give reasons for your answer.

x f(x)

0 5

2 7

4 9

6 11

g(x)

0 5

1 6

3 7

4 9

x h(x)

2 7

5 16

8 25

12 37

6. If a linear function has positive slope, does its graph slope upward or downward? What

if the linear function has negative slope?

7. Is a linear function? If so, find the slope and the y-intercept of the graph of f.

8. (a) Graph for , m ⫽ 1, and m ⫽ 2, all on the same set of axes. How

does increasing the value of m affect the graph of f ?

(b) Graph for , b ⫽ 1, and b ⫽ 2, all on the same set of axes. How

does increasing the value of b affect the graph of f ?

b =

f 1x 2= x + b

m =

f 1x 2= mx

f 1x 2= 2

x f(x)

0 8

1 5

2 2

- 1

162 CHAPTER 2

■

Linear Functions and Models

SKILLS

9–16 ■ Determine whether the given function is linear.

9. 10.

11. 12.

13. 14.

15. 16.

17–20

■ For the given linear function, make a table of values and sketch its graph.

17. 18.

19. 20.

21–24 ■ For the given linear function, find the average rate of change on the following intervals.

(a) Between and x ⫽ 1

(b) Between x ⫽ 1 and x ⫽ 2

21. 22.

23. 24.

25–34

■ For the given linear function,

(a) Sketch the graph.

(b) Find the slope of the graph.

25. 26.

27. 28.

29. 30.

31. 32.

33. 34.

35–38

■ A verbal description of a linear function is given. Find the function.

35. The linear function f has rate of change 7 and initial value

36. The linear function has rate of change and initial value .

37. The graph of the linear function h has slope and y-intercept 9.

38. The graph of the linear function k has slope 2.5 and y-intercept 10.7.

39–42

■ A table of values for a linear function f is given.

(a) Find the rate of change and the initial value of f.

(b) Express f in the form .

39. 40. 41. 42.

x f(x)

-3

0 6

6 8

15 11

x f(x)

-2

0 12

1 10

3 6

-2

x f(x)

0 3

2 4

4 5

6 6

f 1x 2= b + mx

- 3

- 3.

F 1x 2=-0.3x - 6F 1x 2=-0.5x - 2

h 1t 2=-3t - 9h 1t 2= 2t - 6

f 1t 2= 4 + 2tf 1t 2= 6 + 3t

g1x 2=-2x + 10g1x 2=-3 - x

f 1x 2= 3 - 4xf 1x2= 4 + 2x

s 1x 2=-3x - 9

h 1x 2=-2x - 5

g1x 2= 5 + 15xf 1x 2= 4 + 2x

x = a + h

x =-1

s 1t 2=-2t - 6h 1t2= 6 - 3t

g1x 2= 4 + 2xf 1x 2= 6x + 5

f 1x 2= 12t + 72

f 1x 2=

1t - 22

f 1x 2=

x - 3

f 1x 2=-x + 26

f 1x 2= 15 + 2xf 1x 2= 4 - x

f 1x 2= 8 -

xf 1x 2= 3 +

SECTION 2.2

■

Linear Functions: Constant Rate of Change 163

43–48 ■ Find the slope of the line passing through the two given points.

43. (0, 0) and (4, 2) 44. (0, 0) and (2, ⫺6)

45. (2, 2) and (⫺10, 0) 46. (1, 2) and (3, 3)

47. (2, 4) and (4, 3) 48. (2, ⫺5) and (⫺4, 3)

49–52

■ The graph of a linear function f is given.

(a) Find the slope and the y-intercept of the graph.

(b) Express f in the form .

49. 50.

51. 52.

f 1x 2= b + mx

53. Landfill The amount of trash in a county landfill is modeled by the function

where x is the number of days since January 1, 1996, and is measured in thousands

of tons.

(a) Is T a linear function?

(b) What is the initial amount of trash in the landfill in 1996?

(d) Sketch a graph of T.

54. Cell Phone Costs Ingrid is in the process of choosing a cell phone and a cell phone

plan. Her choice of phones and plans is as follows:

Phones: $50 (basic phone), $100 (camera phone)

Plans: $30, $40, or $60 per month

The first graph on the following page represents the cost per month of cell phone

service for the $30 plan; the second graph represents the total cost of purchasing

the $50 cell phone and receiving cell phone service for x months at $40 per month.

(a) Why is the line in the first graph horizontal?

(b) What do the x and y coordinates in the graph of C (second graph) represent?

C 1x2

T1x 2

T1x 2= 32,400 + 4x

1_1 234

CONTEXTS