Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

174 CHAPTER 2

■

Linear Functions and Models

6. The graph of the general linear equation is a

_______. The graph of

the equation is a line with x-intercept

_______ and y-intercept

_______.

Think About It

7. Suppose that the graph of the outdoor temperature over a certain period of time is a line.

How is the weather changing if the slope of the line is positive? If it is negative? If it is

zero?

8. Find equations of two different lines with y-intercept 5. Find equations of two different

lines with slope 5. Can two different lines with the same slope have the same

y-intercept?

9. Suppose you want to find out whether three points in a coordinate plane lie on the same

line. How can you do that using slopes? Can you think of another method?

10. Suppose that you know the slope and two points on a line. To find an equation for the

line, it doesn’t matter which of the two points we use in the point-slope form.

Experiment with the line and points shown in the figure to the left by finding the point-

slope equation of the line in two different ways: first using the point (1, 2), and then

using the point (2, 5). Compare your answers by putting each of the equations you

found into slope-intercept form. Do you get the same equation in each case?

3x + 5y - 15 = 0

Ax + By + C = 0

(1, 2)

(2, 5)

m=3

SKILLS

11–16 ■ Find an equation of the line with the given slope and y-intercept.

11. Slope 5, y-intercept 2 12. Slope 2, y-intercept 7

13. Slope , y-intercept 14. Slope , y-intercept

15. Slope , y-intercept 5 16. Slope , y-intercept

17–22

■ Express the given equation in slope-intercept form.

17. 18.

19. 20.

21. 22.

23–30

■

(a) Find an equation of the line with the given slope that passes through the given point.

(b) Simplify the equation by putting it into slope-intercept form.

23. Slope 2, through (0, 4) 24. Slope , through

25. Slope , through (1, 7) 26. Slope , through (1, 6)

27. Slope , through 28. Slope , through

29. Slope 0, through 30. Slope 0, through

31–36

■ Two points are given.

(a) Find an equation of the line that passes through the given points.

(b) Simplify the equation by putting it in slope-intercept form.

31. and (4, 7) 32. and (1, 2)

33. and 34. and (3, 7)

35. (2, 3) and (5, 7) 36. and (5, 3)12, - 12

1- 1, - 1212, - 221- 1, 72

1- 1, 621- 2, 12

1- 1, 1214, - 52

1- 4, - 32-

1- 6, 42-

- 3

10, - 22

4y + 8 = 04y + 5x = 10

2x - 8y + 5 = 09x - 3y - 4 = 0

x + 4y = 103x + y = 6

- 1- 5- 3- 1

SECTION 2.3

■

Equations of Lines: Making Linear Models 175

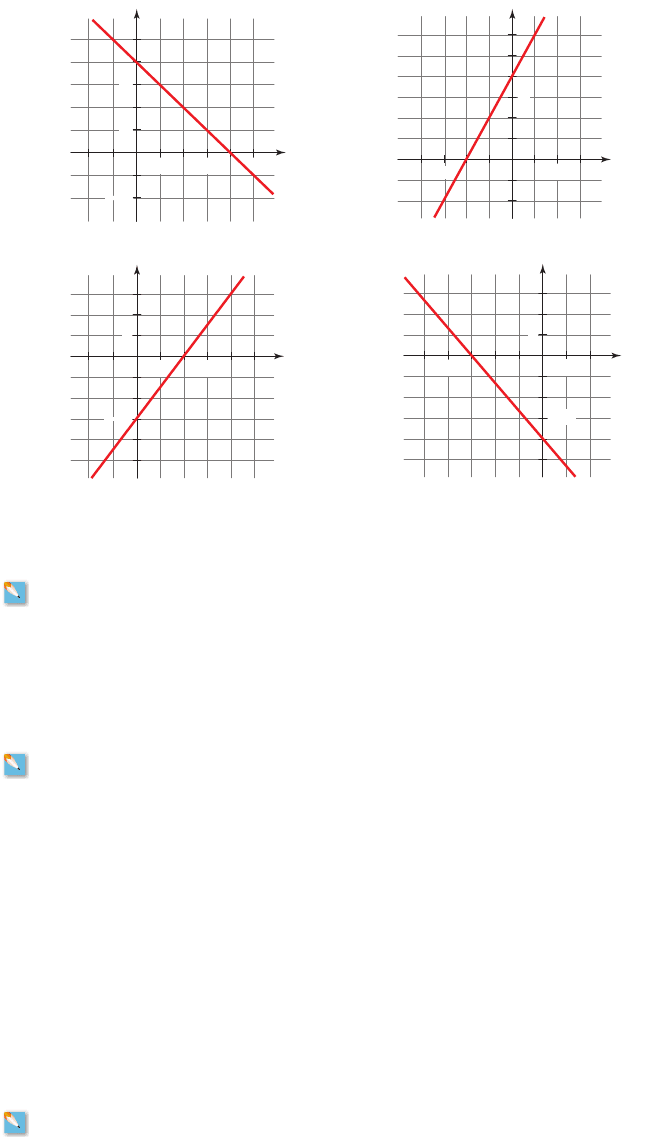
37–40 ■ Find an equation in slope-intercept form for the line graphed in the figure.

37. 38.

39. 40.

41–44 ■ Find an equation of the horizontal line with the given property.

41. Has y-intercept

42. Has y-intercept 3

43. Passes through the point (8, 10)

44. Passes through the point

45–48

■ Find an equation of the vertical line with the given property.

45. Has x-intercept 8

46. Has x-intercept

47. Passes through the point (8, 10)

48. Passes through the point

49–52

■ An equation of a line is given. Find the slope and y-intercept of the line.

49. 50.

51. 52.

53–56 ■ A general linear equation is given.

(a) Find the slope of the line.

(b) Find the x- and y-intercepts.

53. 54.

55. 56. - 3x + 2y + 1 = 04x - 5y - 10 = 0

2x - 7y + 14 = 03x + 5y - 15 = 0

- 3x - 7y = 42- 6x = 15 - 5y

5x = 20 + 2y3x + 4y = 24

1- 1, 22

- 3

1- 1, 22

- 7

135

176 CHAPTER 2

■

Linear Functions and Models

57. Air Traffic Control Air traffic controllers at most airports use a radar system to

identify the speed, position, and other information about approaching aircraft. Using

radar, an air traffic controller identifies an approaching aircraft and determines that it is

45 miles from the radar tower. Five minutes later, she determines that the aircraft is 25

miles from the radar tower. Assume that the aircraft is approaching the radar tower

directly at a constant speed.

(a) Find a linear equation that models the distance y of the aircraft from the radar tower

x minutes after it was first observed.

(b) What is the speed of the approaching aircraft?

58. Depreciation A small business owner buys a truck for $25,000 to transport supplies

for her business. She anticipates that she will use the truck for 5 years and that the truck

will be worth $10,000 in 5 years. She plans to claim a depreciation tax credit using the

straight-line depreciation method approved by the Internal Revenue Service. This

means that if V is the value of the truck at time t, then a linear equation is used to relate

V and t.

(a) Find a linear equation that models the depreciated value V of the truck t years since

it was purchased.

(b) What is the rate of depreciation?

59. Depreciation A small business buys a laptop computer for $4000. After 4 years the

value of the computer is expected to be $200. For accounting purposes the business uses

straight-line depreciation (see Exercise 58) to assess the value of the computer at a

given time.

(a) Find a linear equation that models the value of the computer t years since its

purchase.

(b) Sketch a graph of this linear equation.

(d) Find the depreciated value of the computer 3 years from the date of purchase.

60. Filling a Pond A large koi pond is filled with a garden hose at a rate of 10 gallons per

minute. After 5 minutes the pond has 350 gallons of water. Find a linear equation that

models the number of gallons y of water in the pond after t minutes.

61. Weather Balloon A weather balloon is filled with hydrogen at the rate of /s.

After 2 seconds the balloon contains of hydrogen. Find a linear equation that

models the volume of hydrogen in the balloon at any time t.

62. Manufacturing Cost The manager of a furniture factory finds that the cost of

manufacturing chairs depends linearly on the number of chairs produced. It costs $2200

to make 100 chairs and $4800 to make 300 chairs.

(a) Find a linear equation that models the cost y of making x chairs, and sketch a graph

of the equation.

(b) How much does it cost to make 75 chairs? 425 chairs?

(d) Find the y-intercept of the line. What does it represent?

63. Demand for Bird Feeders A community bird-watching society makes and sells

simple bird feeders to raise money for its conservation activities. They sell 20 per week

at a price of $10 each. They are considering raising the price, and they find that for

every dollar increase, they lose two sales per week.

(a) Find a linear equation that models the number y of feeders that they sell each week

at price x, and sketch a graph of the equation.

(b) How many feeders would they sell if they charged $14 per feeder? If they

charged $6?

5 ft

0.5 ft

CONTEXTS

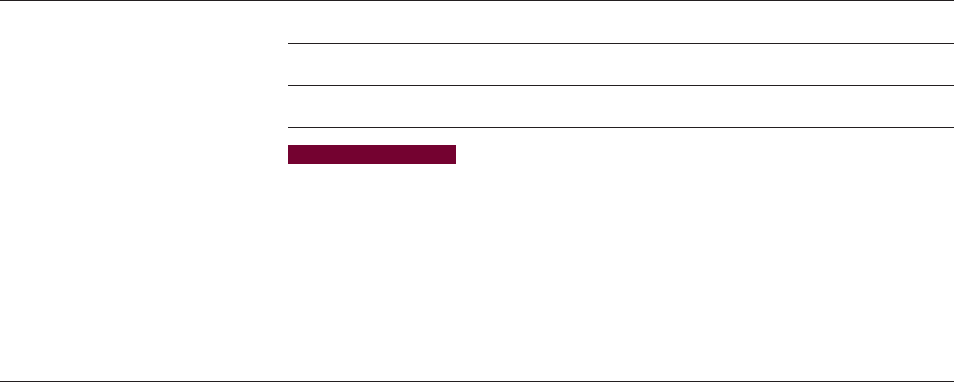
SECTION 2.4

■

Varying the Coefficients: Direct Proportionality 177

(d) Find the y-intercept of the line. What does it represent?

(e) Find the x-intercept of the line. What does it represent?

64. Crickets and Temperature Biologists have observed that the chirping rate of

crickets of a certain species is related to temperature, and the relationship appears to be

very nearly linear. A cricket produces 120 chirps per minute at and 168 chirps per

minute at .

(a) Find a linear equation that models the temperature T when crickets are chirping at

x chirps per minute. Sketch a graph of the equation.

(b) If the crickets are chirping at 150 chirps per minute, estimate the temperature.

80°F

70°F

2.4 Varying the Coefficients: Direct Proportionality

■

Varying the Constant Coefficient: Parallel Lines

■

Varying the Coefficient of x: Perpendicular Lines

■

Modeling Direct Proportionality

IN THIS SECTION… we explore how changing the coefficients b and m in the linear

equation affects the graph. We’ll see that these coefficients tell us when two

linear equations represent parallel or perpendicular lines. We’ll also see that the number m

plays a crucial role in modeling real-world quantities that are “directly proportional.”

We know that the graph of a linear equation is a line. How does vary-

ing the numbers b and m change this line? That is the question we seek to answer in

this section.

y = b + mx

■ Varying the Constant Coefficient: Parallel Lines

The coefficients of a linear equation are the numbers b and m. The num-

ber b is called the constant coefficient, and m is called the coefficient of x.

We know that the constant coefficient b is the y-intercept of the line. So if we

vary the constant b, we change only the y-intercept of the line; the slope remains the

same. The next example illustrates the effect of varying the constant term.

y = b + mx

example

Graphing a Family of Linear Equations

Sketch graphs of the family of linear equations for .

How are the graphs related?

Solution

We need to sketch graphs of the following six linear equations:

The graphs are shown in Figure 1 on page 178.

y = 2 + 2x y = 3 + 2x y = 4 + 2x

y =-1 + 2x y = 0 + 2x y = 1 + 2x

b =-1, 0, 1, 2, 3, 4y = b + 2x

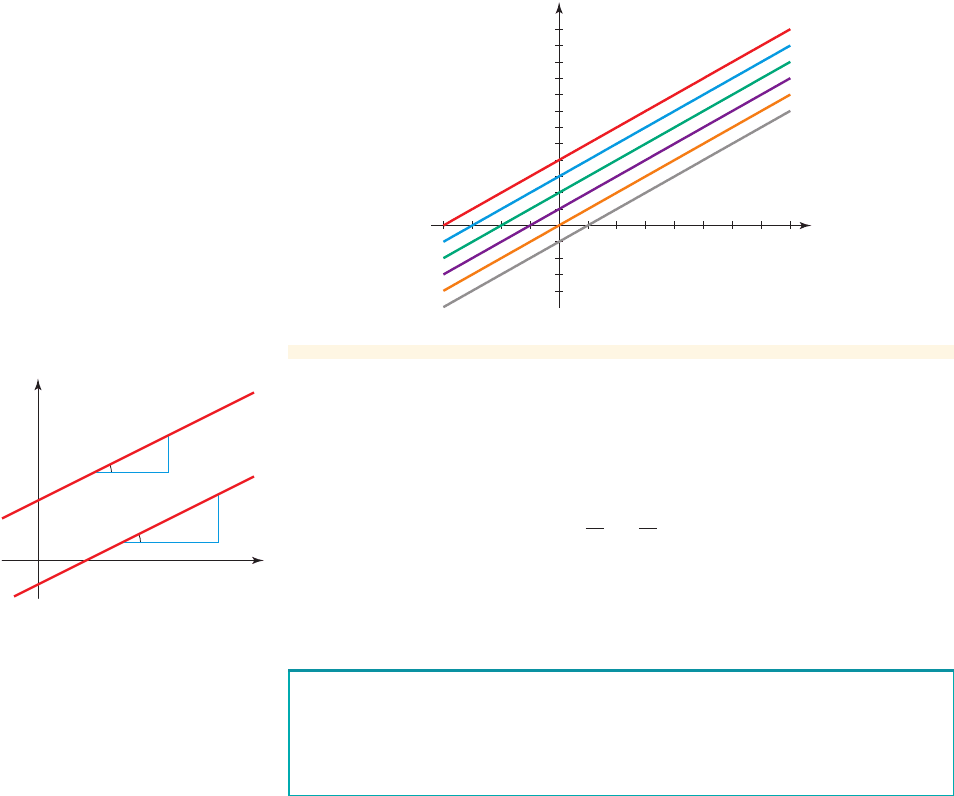
178 CHAPTER 2

■

Linear Functions and Models

12_1_2 3 4

figure 1 Graph of the family of

lines , b =-1, 0, 1, 2, 3y = b + 2x

■ NOW TRY EXERCISE 9 ■

All the lines in Example 1 have the same slope. Since slope measures the steep-

ness of a line, it seems reasonable that lines with the same slope are parallel. To prove

this, let’s consider any two parallel lines and with slopes , as shown in

Figure 2. Since the triangles shown are similar, the ratios of their sides are equal:

Conversely, if the slopes are equal, then the triangles will be similar, so corre-

sponding angles are equal and the lines are parallel.

⫽

⫽ m

and m

l¤

b¤

a¤

l⁄

a⁄

b⁄

figure 2 Lines with the same

slope are parallel.

Suppose that two nonvertical lines have slopes and . The lines are

parallel if and only if their slopes are the same:

= m

Parallel Lines

example

Finding Equations of Parallel Lines

Let l be the line with equation .

(a) Find an equation for the line parallel to l and passing through the point (2, 0).

(b) Sketch a graph of both lines.

Solution

(a) The line has slope . So the line we want also has slope . A

point on the line is (2, 0). Using the point-slope form, we get

Point-slope form

Replace m by , by 2, and by 0

Distributive Property

So an equation for the line is .y = 6 - 3x

y =-3x + 6

- 3 y - 0 =-31x - 2 2

y - y

= m 1x - x

, y

- 3- 3y = 4 - 3x

y = 4 - 3x

Each of these lines has the same slope (but not the same y-intercept).

SECTION 2.4

■

Varying the Coefficients: Direct Proportionality 179

(b) A graph of the lines is shown in Figure 3.

figure 3 Graphs of

and y = 6 - 3x

y = 4 - 3x

■ NOW TRY EXERCISE 13 ■

example

Trains

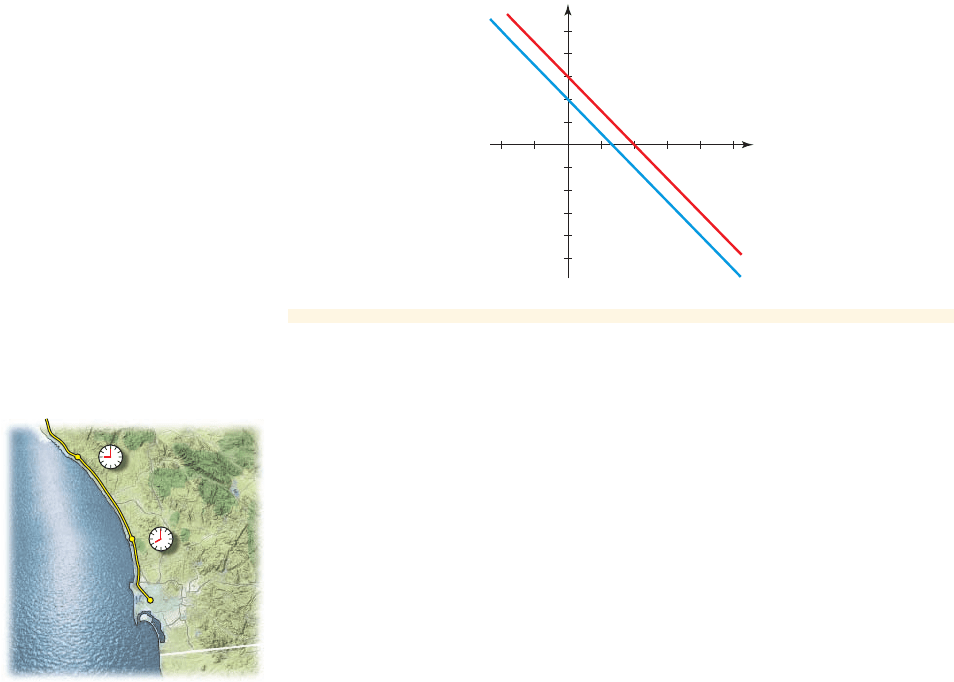
Two trains are heading north along the California coast on the same track. The first

train leaves Solana Beach 25 miles north of San Diego at 8:00 A.M.; the second train

leaves San Clemente 58 miles north of San Diego at 9:00 A.M. Each train maintains

a constant speed of 80 miles per hour.

(a) For each train, find a linear equation that relates its distance y from San Diego

at time t.

(b) Sketch graphs of the linear equations you found in part (a).

Solution

(a) For each train we need to find an equation of the form

Since each train travels at a speed of 80 mi/h, we have m ⫽ 80 for each train.

Let’s take time t ⫽ 0 to be 8:00

A.M., so 9:00 A.M. would be time t ⫽ 1. Let y be

the distance north of San Diego.

■

For the first train, y ⫽ 25 when t ⫽ 0, so the point (0, 25) is on the desired

line. Using the point-slope formula for the equation of a line, we get

Point-slope form

Replace m by 80, t

by 0, and y

by 25

Add 25

■

For the second train, y ⫽ 58 when t ⫽ 1, so the point (1, 58) is on the

desired line. Using the point-slope formula for the equation of a line, we get

Point-slope form

Replace m by 80, t

by 1, and y

by 58

Distributive Property

Add 58

y =-22 + 80t

y - 58 = 80t - 80

y - 58 = 801t - 1 2

y - y

= m 1t - t

y = 25 + 80t

y - 25 = 801t - 0 2

y - y

= m 1t - t

y = b + mt

San Diego

Solana Beach

San

Clemente

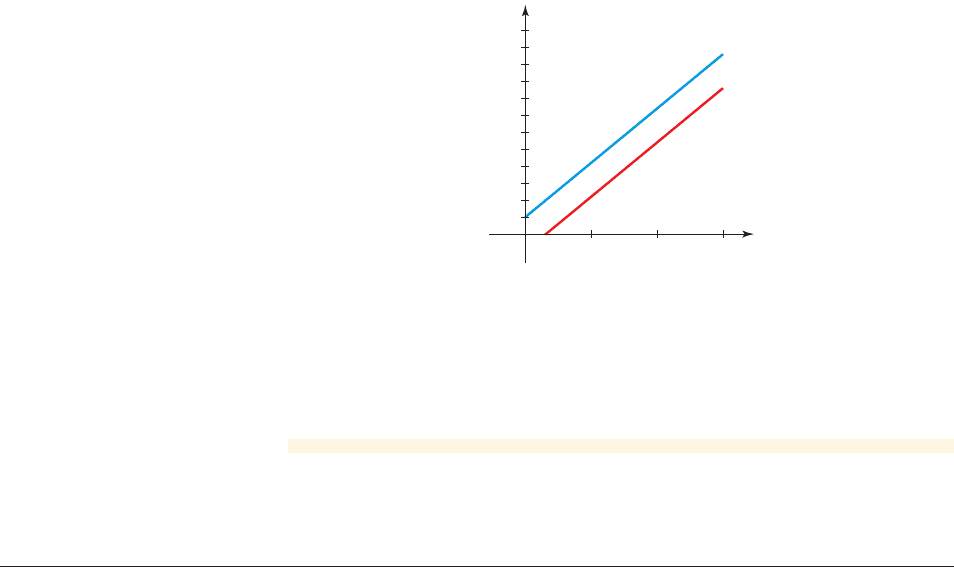
(b) The two equations are graphed in Figure 4. We know that the two lines are

parallel because each has the same slope m ⫽ 80.

100

200

300

y=25+80t

y=_22+80t

figure 4

180 CHAPTER 2

■

Linear Functions and Models

■ Varying the Coefficient of x: Perpendicular Lines

For a linear equation we know that m, the coefficient of x, is the slope

of the line. So if we vary m, we change how the line “leans.” The next example il-

lustrates this effect.

y = b + mx

trains will never be at the same place at the same time; hence they won’t

collide.

■ NOW TRY EXERCISE 51 ■

example

Graphing a Family of Linear Equations

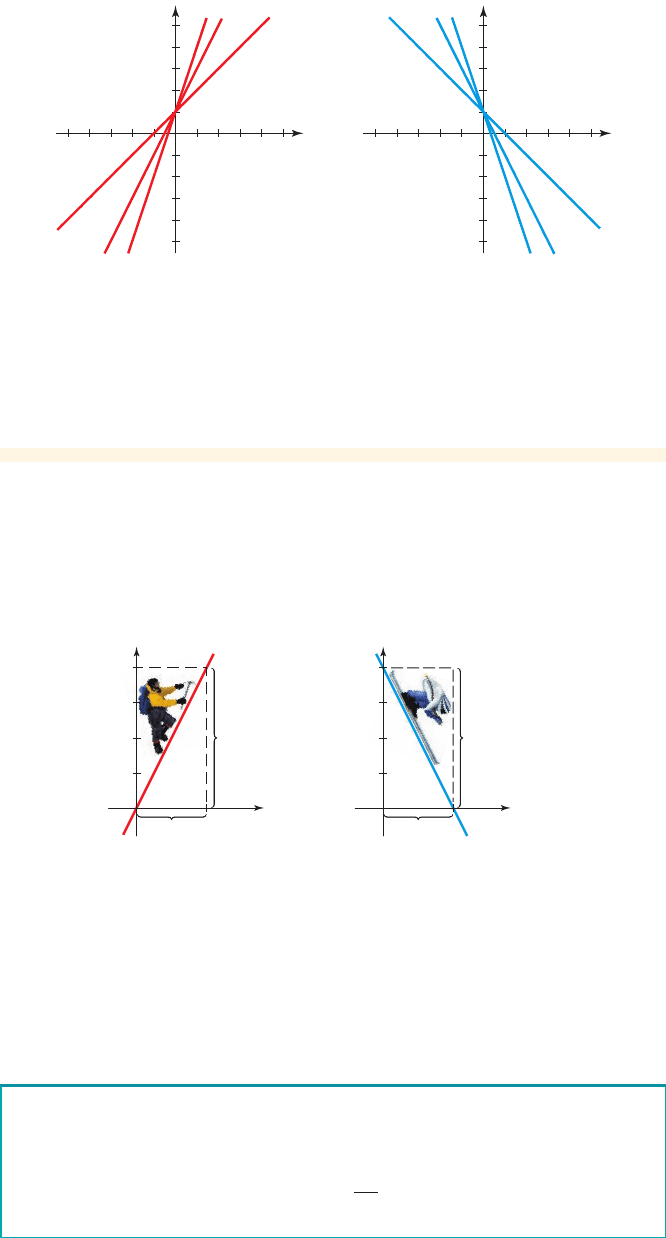
Sketch graphs of the family of linear equations for the following values

of m.

(a)

(b)

Solution

(a) We need to sketch graphs of the following linear equations:

The graphs are shown in Figure 5(a).

(b) We need to sketch graphs of the following linear equations:

The graphs are shown in Figure 5(b).

y = 1 - xy = 1 - 2xy = 1 - 3x

y = 1 + xy = 1 + 2xy = 1 + 3x

m =-1, - 2, - 3

m = 1, 2, 3

y = 1 + mx

SECTION 2.4

■

Varying the Coefficients: Direct Proportionality 181

the larger the slope, the more steeply the line rises as we move from left to right.

When the slope is negative, the line falls as we move from left to right.

■ NOW TRY EXERCISE 11 ■

From Example 4 we see that lines with positive slope slant upward to the right,

whereas lines with negative slope slant downward to the right. This observation is il-

lustrated in Figure 6. The steepest lines are those for which the absolute value of the

slope is the largest.

(

)

m=1, 2, 3

(

)

m=_1, _2, _3

figure 5 Graph of a family of lines y = 1 + mx

Run

Rise:

Run

change in

y-coordinate

(positive)

Rise:

change in

y-coordinate

(negative)

figure 6 If the rise is positive, the slope is positive. If the

rise is negative, the slope is negative.

If two lines are perpendicular, how are their slopes related? Since perpendicular

lines “lean” in different directions, we expect that their slopes would be quite differ-

ent. In fact, if the slope of a line is positive, we can see that the slope of a perpendi-

cular line should be negative. The exact relationship is as follows.

Suppose that two nonvertical lines have slopes and . The lines are

perpendicular if and only if their slopes are negative reciprocals:

Perpendicular Lines

182 CHAPTER 2

■

Linear Functions and Models

Why do perpendicular lines have negative reciprocal slopes? To answer this

question, let’s consider two perpendicular lines l

and l

as shown in Figure 7.

example

Finding Equations of Lines Parallel and Perpendicular

to a Given Line

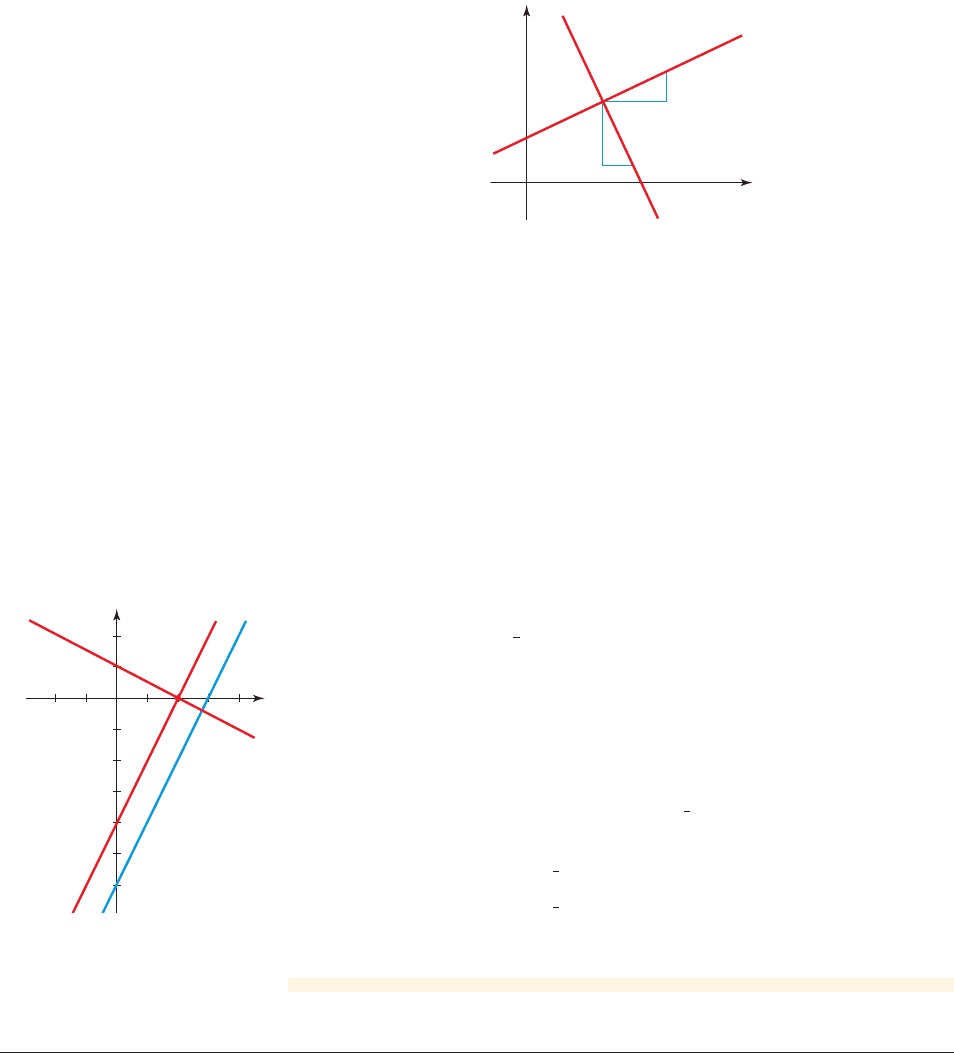
Let l be the line with equation . Find equations for two lines that pass

through the point (2, 0), one parallel to l and one perpendicular to l. Sketch a graph

showing all three lines.

Solution

The line has slope 2, so the parallel line also has slope 2, and the per-

pendicular line has slope , the negative reciprocal of 2. We use the point-slope

form in each case to find the equation of the line we want.

■

Parallel line: Using slope m ⫽ 2 and the point (2, 0), we get the equation

Point-slope form

Simplify

■

Perpendicular line: Using slope and the point (2, 0), we get the

equation

Point-slope form

Simplify

All three lines are graphed in Figure 8.

■ NOW TRY EXERCISE 19 ■

y =-

x + 1

y - 0 =-

1x - 2 2

m =-

y = 2x - 4

y - 0 = 21x - 2 2

y = 2x - 6

l⁄

l¤

figure 7 Perpendicular lines

Perpendicular

Parallel

figure 8

Since the lines are perpendicular, the two right triangles in the figure are con-

gruent. From the figure we see that the slope of l

is and the slope of l

is ⫺

(since the rise for l

is negative). This means that the slopes are negative reciprocals

of each other.

b>aa>b

■ Modeling Direct Proportionality

The electrical capacity of solar panels is directly proportional to the surface area of

the panels. This means that if we double the area of the panels, we double the elec-

trical capacity; if we triple the area of the panels, we triple the electrical capacity;

SECTION 2.4

■

Varying the Coefficients: Direct Proportionality 183

and so on (see Figure 9). This type of relationship between two variables is called di-

rect proportionality and is described by a linear equation.

Notice that the equation that defines direct proportionality is a linear equation

with y-intercept 0. The graph of this linear equation is a line passing through the ori-

gin with slope k.

figure 9 Doubling the area of a solar panel doubles the electrical capacity

We say that the variable y is directly proportional to the variable x (or y

varies directly as x) if x and y are related by an equation of the form

y ⫽ kx

The constant k is called the constant of proportionality.

Direct Proportionality

example

Direct Proportionality

A solar electric company installs solar panels on the roofs of houses. A customer is in-

formed that when 12 solar panels are installed, they produce 2.4 kilowatts of electricity.

(a) Find the equation of proportionality that relates the number of panels installed

to the number of kilowatts produced.

(b) How many kilowatts of electricity are produced by 16 panels?

Solution

(a) The equation of proportionality is an equation of the form y ⫽ kx, where x

represents the number of solar panels and y represents the number of kilowatts

produced. To find the constant k of proportionality, we replace x by 12 and y

by 2.4 in the equation.

Equation of proportionality

Replace x by 12 and y by 2.4

Divide by 12, and switch sides

Calculate

k = 0.2

k =

2.4

2.4 = kⴢ 12

y = kx